概率化预测隧道地质条件

寇冰清 KOU Bing-qing；宋永发 SONG Yong-fa

（大连理工大学建设工程学部，大连 116024）

（Faculty of Infrastructure Engineering，Dalian University of Technology，Dalian 116024，China）

概率化预测隧道地质条件

寇冰清 KOU Bing-qing；宋永发 SONG Yong-fa

（大连理工大学建设工程学部，大连 116024）

（Faculty of Infrastructure Engineering，Dalian University of Technology，Dalian 116024，China）

为了预测隧道开挖面前方的地质条件，降低施工风险和成本，采用马尔科夫和神经网络构成的模型，既比马尔科夫方法经济，又能实现神经网络方法所不能实现的动态化预测。

隧道风险；地质条件；概率化预测；马尔科夫与神经网络

0 引言

地质条件的不确定性是隧道施工不确定性最主要的来源，恰当的估计，既可防止灾难性的后果，也可以通过减少在施工中的保守措施以及选择合适的开挖和支护方法达到节约资源的目的。探测地质条件的方法分为硬方法和软方法，硬方法包括从上往下打钻孔和地质超前预报，软方法更经济，它包括时间序列、神经网络、马尔科夫随机过程等方法[1]。时间序列分析需要大量信息进行趋势的分析和模式的识别。神经网络能很好地处理非线性联系，但它无法实现动态预测。马尔科夫方法将地质参数看作是离散状态、连续空间的随机过程，根据特定位置地质条件及转移概率矩阵预测开挖线上各位置的地质条件，它在实现动态预测时，需要通过试验的方法来获得当前位置的地质条件，往往耗财、费时，实际工程中也不可能大规模进行试验。而将马尔科夫与神经网络相结合既可以实现动态预测，又能节省时间和成本。

1 模型结构

模型结构如图1所示，分为马尔科夫部分和神经网络部分。

1.1 马尔科夫部分 马尔科夫一步记忆可用如下公式描述：p[X（ti+1）=xi+1｜X（ti）=xi，X（ti-1）=xi-1，…，X（t1）=x1)]=p[X（ti+1）=xi+1｜X（ti）=xi]

ti-1，ti，ti+1是沿隧道开挖线上相邻的不同位置，它们间距相同，xi-1，xi，xi+1是相应的地质条件（G1，G2，G3）。转移概率矩阵为：V=[vij]，vij=p[X（ti）=j｜X（ti-1）=i]

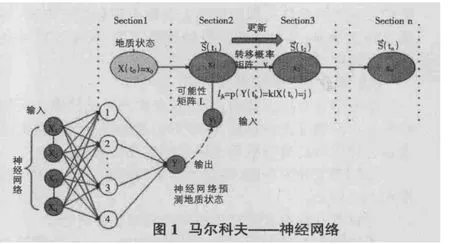
1.2 BP神经网络部分 神经网络模型中的输入参数X1，X2，X3，X4为盾构机每经过一环（大约为 1.4m）所记录的数据，输出 Y 为地质条件（G1=0，G2=0.5，G3=1），神经网络输出值作为输入值传递至马尔科夫模型，可能性矩阵L通过计算神经网络在训练集中预测准确度给出。

2 波尔图案例分析

2.1 波尔图隧道工程概况 波尔图地铁地下部分包括两条隧道（C线和S线）。C线长约2.5km，于2000年6月开始选用直径为8.7m的海瑞克土压平衡式盾构施工，该机器在地质条件良好的情况下采用全开式开挖方式，在地质条件不好的情况下采用全封闭式开挖方式。隧道于2002年10月顺利完工[3]。

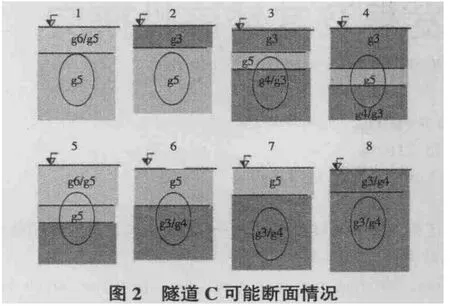
2.2 神经网络输入和输出参数 输入参数为盾构机在掘进过程中，每隔10s记录的贯入速度（mm/转）、刀盘扭矩(MN.m)、总推力（KN）、刀盘切割力（KN）。输出参数为根据岩土的风化程度、破裂程度及断面情况进行的分类（G1，G2，G3）。隧道穿过的岩层分为g1-g7。g1-g4为岩石类，g5-g6是土体类，g7是人工材料和冲积土。根据工程信息，隧道土体有八种断面情况（图2[4]），将这八种断面情况进行如下简化：土体（G1），混合体（G2），岩体（G3）。土体（G1）对应情况1、2—开挖断面全部由土体构成（g5和g6）；岩体（G3）对应于情况7、8—开挖断面全部为岩石成分（g3和g4）；混合体则是由岩石和土体共同构成。

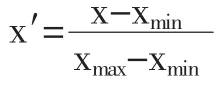
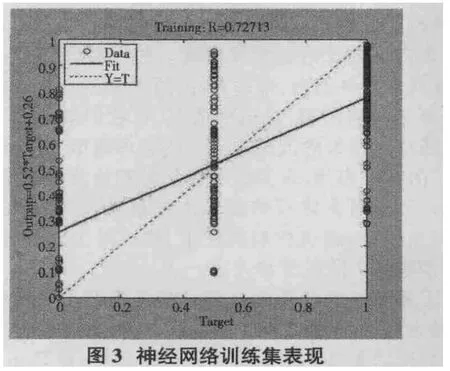
通过对神经网络在训练集中输出结果分析确定如下判别区间：当输出结果落入[0，0.17]时，判断其为0，即神经网络输出为 G1；落入（0.17，0.49]时，判断其为 0.5，为 G2；落入[0.49，1]时，判断其为1，为G3。由此得到可能性矩阵如表1所示。将训练集的395组数据按前述公式计算，得到马尔科夫模型转移概率矩阵，如表2所示。

2.4 动态预测及结果 根据已知地质条件（R400、R416等）及V，求出检验集中地质条件的先验概率。当运行到第Rr-1，将记录下的参数输入至神经网络，得到输出值，通过判别区间判断神经网络预测地质条件，再结合Rr-1先验地质条件概率计算Rr-1后验地质条件概率，根据V更新Rr先验地质条件概率，当盾构机运行至Rr，重复这一过程。检验集共347组数据，其中G1有114组数据，模型将其中111组预测为G1(97.37%)、3组预测为G2(2.63%)；G2有数据118组，模型将其中58组预测为G1(49.15%)，54组预测为G2(45.77%)，6组预测为G3(5.08%)；G3共有数据115组，模型将18种预测为G1(15.65%)，13组(11.30%)预测为G2，84组 (73.05%)预测为G3，总预测准确率为71.76%。模型预测结果如表3所示，图4为隧道部分区段预测情况。

表1 可能性矩阵

表2 转移概率矩阵表

表3 模型预测总体情况

3 结论

对地质条件恰当的估计既能降低风险，又能节约成本。一个马尔科夫-神经网络模型被用来动态的、低成本的、大规模的预测波尔图隧道盾构机开挖面前方的地质条件，395组数据被用于训练模型，347组数据被用来检验模型。在岩体和土体中模型表现很好，而在混合体中模型预测准确率有所下降，模型整体预测准确率为71.76%。在岩体中，盾构机可以采用全开模式运行可以节约费用，在土体中，盾构机采用全封闭模式运营可以降低风险。这对于施工者选择合适的开挖方式和支护方式有一定的借鉴作用。

[1]GUAN Zhenchang.Markovian Geology Prediction Approach and Its Application in Mountain Tunnels [J].Tunnelling and Underground Space Technology，2012(31)：61-62.

[2]Suchatvee S.Artificial Neural Networks for Predicting the Maximum Surface Settlement Caused by EPB Shield Tunneling[J].Tunnelling and Underground Space Technology，2006(21)：133-150.

[3]、[4]Rita S.Risk Analysis for Tunneling Projects[D].Massachusetts.Massachusetts Institute of Technology,2010.

Probabilistic Prediction of Tunnel Geological Conditions

In order to predict the geological conditions ahead of tunnel face,a hybrid approach combining Markov process with neural networks is presented,it's cheaper than using Markov process alone and can let dynamic prediction the neural networks can't achieve come true.

tunnel risks；geological conditions；probabilistic prediction；Markov and neural networks approach

寇冰清（1990-），男，湖北荆门人，硕士研究生，研究方向为工程管理、隧道风险管理；宋永发（1963-），男，吉林省吉林市人，副教授，博士，研究方向为隧道风险管理、轨道交通。

U45

A

1006-4311（2014）11-0100-02