土工试验中线性回归应用分析
2014-04-16黄聿銮HUANGYuluan
黄聿銮 HUANG Yu-luan
(福建省地质工程勘察院,福州 350000)
(Fujian Geological Engineering Investigation Institute,Fuzhou 350000,China)
1 土工试验数据
传统的土工试验数据是通过记录、计算、绘制曲线再间接计算出来的。记录工作量大,误差大,存在错记、漏记现象;传统计算与绘图速度慢、效率低,难以满足现代工程勘察要求。
近年来,线性回归处理法被一些实验室相继应用,很好地解决大量试验数据处理的问题。
本实验室依据直接剪切试验中的剪应力τ与压力p呈现线性关系,液塑限联合试验中圆锥下沉的深度h和含水率ω的双对数呈现线性关系,选择了某土工试验科技公司的采集系统对土样的直接剪切试验的粘聚力c、摩擦角φ,液塑限联合试验液限ωL、塑限ωP进行采集、计算和求解。
由于土样的差异性,试验数据各点往往不在一条直线上;试验数据表明,只有相关系数r≥0.95时才能得到较为可靠的计算结果,否则应仔细检查相关原因,而后重新确定补做的试验。
2 土工试验中的线性方程
在土工试验中,用线性方程的方法计算较为准确,也较为简单,根据其数值变化就可以总结出线性方程的回归方程式。例如y=a+bx,a为常数项,b为回归系数。线性方程中的a、b、x、y等相关系数的估计值计算表达式为:


根据上述公式,通过具体试验中若干组x、y值的测定,就能计算出 a、b和 x、y的值。
3 直剪试验中线性回归法分析
直剪试验是用来确定土的c、φ值,在现行国家、行业等标准中是通过对同一土样取4个以上试样分别在不同的垂直压力下的抗剪强度值的测定,做出相应的关系曲线图,而所画出的p-τ曲线图上的点往往不能连成一条直线,而根据莫尔一库伦强度理论用一条直线近视地代替,从而确定土的粘聚力c、摩擦角φ值。
这种作图法容易造成的人为误差和经验误差,并且工作量大、操作较慢。
线性回归能够有效解决作图引发的问题,在实际计算中依据两个变量成正比例关系τ=c+ptanφ,对任一试样多点的直剪试验压力值p以及剪应力值τ输入τ=c+ptanφ线性回归方程式,由此可通过计算得出正确的粘聚力c和摩擦角φ的值。曲线值中的任意四个点之间的相关系数r≥0.95,则该组样的相关性能较好,否则将重新补点测试。
表1、表2是某边坡、某工民建土样的直剪试验数据处理结果。
表1、表2通过作图法和线性回归法两种数据处理结果进行比较与分析,表1c值最大绝对误差为0.20kPa,平均绝对误差为0.08kPa,φ值最大绝对误差为0.2°,平均绝对误差为0.1°;表2c值最大绝对误差为0.20kPa,平均绝对误差为0.11kPa,φ值最大绝对误差为0.1°,平均绝对误差为0.1°。可见误差很微小,在允许误差范围内,同时回归计算利用了线性关系,有理论依据,其结果更具有合理性。由此可知,线性回归法可用于直剪试验的数据整理中。
4 液塑线联合试验中线性回归分析
现行国家、行业等标准的液塑限联合试验是利用圆锥的下沉深度以及含水率之间的双对数的线性关系,使用作图法得出了试样的液限值ωL和塑限值ωP。
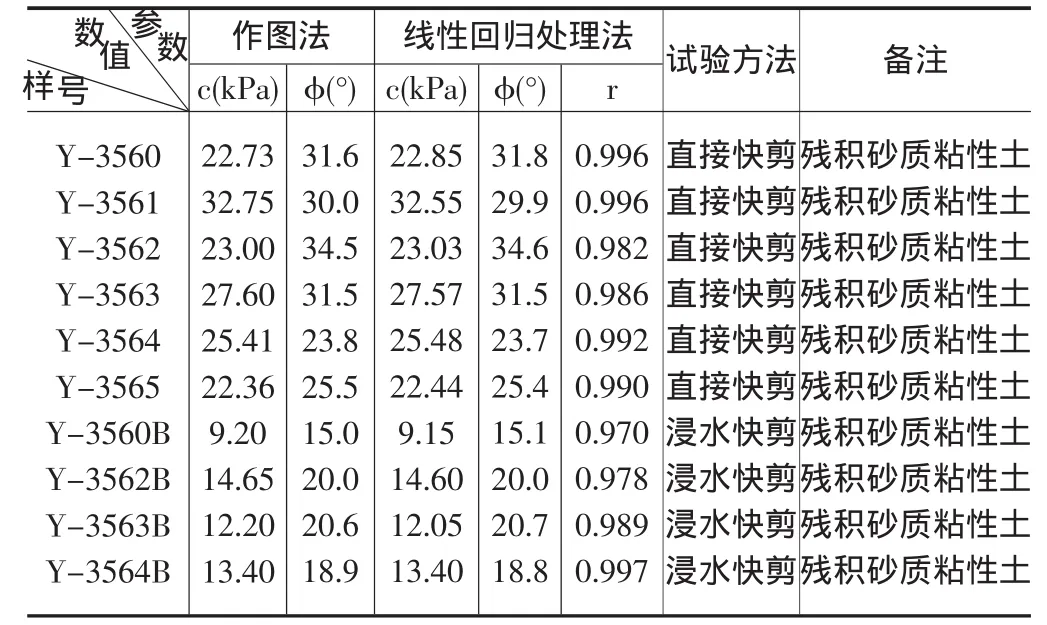
表1 某边坡勘察土样直剪试验参数

表2 某工民建勘察土样直剪试验参数

表3 某公路勘察土样液塑限试验参数

表4 某工民建勘察土样液塑限试验参数
试验中按照相应的规定所测定的点数不应少于三点,并且规定每个点数所对应的圆锥入土深度范围约为3~4mm、7~9mm、15~17mm。由于试验误差,双对数坐标图上的三点往往不在一条直线上,根据规程应用作图法求算液、塑限值。
具体做法是:通过高含水率的点和其余两点连成两条直线,在下沉为2mm处查得相应的两个含水率,当两个含水率的差值小于2%时,以两点含水率的平均值与高含水率的点连成一直线,在双对数坐标图上读10mm、17mm的液限,2mm的塑限。当两个含水率的差值大于、等于2%时,应重做试验。作图法主要的问题在于操作相对缓慢,计算效率不高,并且容易引发较大的误差。
线性回归法则能有效减少液塑限试验的数据处理误差,能从繁琐的作图、计算工作中解放出来。在使用线性回归方法计算液限和塑限值的过程中,利用圆锥入土深度h(mm)以及含水率ω(%)的双对数呈正比例关系logω=a+blogh,通过线性回归计算方式得出了正确的液限和塑限的值。
判定相应的液限和塑限的值是否合格,是否应重做试验,则应通过相关系数r值是否大于等于0.95进行判定。
表3、表4是某公路、某工民建勘察土样液塑限试验数据通过作图法和线性回归算法处理所得结果。
表3、表4通过作图法和线性回归法两种数据处理结果进行比较与分析,表3ωL(100g锥)最大绝对误差为0.2,平均绝对误差为0.1,ωP最大绝对误差为0.1,平均绝对误差为0.1;表4ωL(76g锥)最大绝对误差为0.2,平均绝对误差为0.1,ωP最大绝对误差为0.1,平均绝对误差为0.1。土工试验规程规定:当液塑限小于40时误差为1,等于、大于40时误差为2;而表3、表4误差均小于1,在允许误差范围内,说明线性回归能很好地应用于液塑限试验中。
5 结论
“直剪试验和液塑限测定原理依据库仑定律”是研究土工试验中线性回归最常用的实例,本文也不例外,以此为基础建立的数理关系较为明晰;并且通过采集系统进行计算与画图,避免了传统计算与作图的繁琐和复杂,计算结果精确而快速。这是通过反复计算和检验得出的结论,也是本文不厌花大量试验数据论证得出的结果。同时,体现了线性回归算法相对于原来传统的计算方法的优越性。
比较上述的作图法与线性回归计算结果相差很小,微小的差异也在允许误差范围内。后者最明显的优势在于数据处理中大大缩短了计算时间,同时结果的精确性没有下降,这就是线性回归在土工试验中的应用价值和现实意义。
[1]范孟华.应用最小二乘法和excel图表法处理土工试验数据[J].路基工程,2006(06).
[2]苏巧荣.土工试验数据分析方法探讨[J].河南大学学报(自然科学版),2006(01).
[3]袁聚云.土工试验与原理[M].同济大学出版社,2003.
[4]张克恭,刘松玉等.土力学[M].中国建筑工业出版社,2001.
[5]交通部公路科学研究所.公路土工试验规程(JTGE40-2007)[R].人民交通出版社,2007.
[6]南京水利科学研究院.土工试验规程(SL237-1999)[R].中国水利水电出版社,1999.
[7]国家质量技术监督局,中华人民共和国建设部.土工试验方法标准(GB/T50123-1999)[R].中国计划出版社,1999.
