基于风险中性路径概率的三叉树期权定价模型
2014-10-08元毅YUANYi
元毅 YUAN Yi
(中央财经大学,北京 102206)
(Central University of Finance and Economics,Beijing 102206,China)
0 引言
二叉树模型作为金融资产定价尤其是衍生品定价的数值方法,自从创建以来应用十分广泛。Cox,Ross,Rubinstein在1979年创建的CRR模型,相对于1973年的B-S-M期权定价公式,更易于大家所理解和操作,并且CRR模型可以给美式期权定价,而大名鼎鼎的B-S-M公式则在美式期权上无能为力。虽然二叉树模型仍然是教科书中一个不朽的经典模型,但是在实际操作过程中由于误差精度等问题,其实用性遭到了一定的质疑。在二叉树模型的基础上,我们通过构建一个新的三叉树模型来试图减小模型误差,使得期权价格的数值解可以更接近B-S-M公式所得出的解析解,从而证明三叉树模型的优越性。
1 文献综述
树方法是一个非常流行的期权定价数值方法。它把从现在到到期日的时间分成了n期,使得在这n期里面的股价进行离散地变化。最有名的树方法当属Cox、Ross以及Rubinstein在1979年提出的CRR树。Duffie在1996年证明了当期数n→∞时,CRR模型的解收敛到连续时间模型下期权价格的解,即B-S-M的解析解。然而,收敛的过程既不平滑也很漫长,对于例如障碍期权的一些期权而言,收敛的过程中会出现很明显的震荡情况,Boyle和Lau在1994年的文章中说明了这一点。
三叉树模型最早于1986年由Phelim Boyle提出,作为二叉树模型的一个延伸和扩展,其中的上升因子和下降因子就是由Phelim Boyle提出,至于为什么要选2△t而非二叉树模型中的△t,Boyle的考虑是,首先三叉树中股价有三种变化情况,允许变化的时间更长一些;其次Boyle是在联合两个二叉树之后生成了三叉树,所以相当于两个时间间隔的变化。在此之后Kamrad和Ritchken于1991年发现了另一种形式的三叉树模型,他们对Boyle的三叉树模型做了简化,并且证明了如果从二叉树中的某一阶段跳过下一阶段直接到第三阶段,这样就可以相应产生出一个三叉树。具体见图1。
Kamrad和Ritchken还对上升因子和下降因子进行了处理,使得上升概率、下降概率和保持不变的概率得到了简化,他们加入了参数并且通过寻找最优的使得三叉树计算出来的期权价格向B-S-M公式计算出来的期权价格逼近。总的而言,Kamrad和Ritchken主要关注在阶段少的情况下三叉树的终值情况,并且使得三叉树模型效率更高,运算更快。

图1 二叉树生成三叉树情况
2 基本模型
三叉树模型是一个网格状的用于给期权定价的数值方法模型,它最早于1986年由Phelim Boyle提出。同二叉树模型一样,构建三叉树的目的是为了给期权定价,包括欧式期权和美式期权。定价之前,首先要给出模型中的一些参数,比如股价从时刻到上涨的概率,下降的概率以及保持不变的概率,还有上升幅度,下降幅度等,其次我们要根据以上参数构建股票价格的三叉树模型,最后通过给定的期权价格三叉模型的终端支付运用倒向运算的方法来给初始时刻的期权进行定价。一个单阶段的股票价格树形图见图2。
三叉树模型可以在基于B-SM模型的基础上给出期权定价优良的数值解,其构建过程同构建二叉树的过程十分相似。由于股票价格服从对数正态分布,所以在给参数赋值时需要使得股票价格满足这一要求。正如CRR模型中令和,我们在给参数赋值时同样需要考虑这些问题。
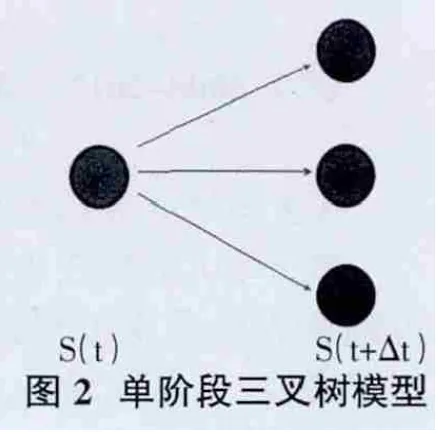

其中股票价格从t到t+Δt变化为S(t)u的概率为pu,变化为S(t)d的概率为pd,根据概率的性质股价不变的概率为pm=1-pu-pd。根据无套利条件和风险中性测度,从t到t+Δt有以下两个式子成立。

认为股票价格遵循对数正态分布,其中σ是标的资产的波动率,r是无风险利率,这两个参数都是常数。由于假定世界是风险中性的,所以假定所有股票的期望收益率为无风险利率,除此之外在之后计算期权的价格时,也以无风险利率作为贴现率进行折现来给期权定价。
除了(1)和(2)之外,给出另一个限制条件,即

虽然这个条件并不总是应用于三叉树建立的过程中的,但是这个条件的成立使得建立的三叉树的节点个数呈现多项式的形式增长而不是以复杂的指数形式增长。
在股价变化幅度u、d以及变化的概率pu、pd和pm都已知的情况下,就可以计算股价S及其变化情况。假定股价从t0开始总共经历了N次变动,其中上升的次数为Nu,下降的次数为Nd,不变的次数为Nm,则Nu+Nd+Nm=N,在N次变动后T时刻的股价为


3 三叉树模型的参数

则ud=1,这是一个典型的交叉树。
尽管《蒙古的人和神》作者亨宁·哈士纶在20世纪30年代曾造访新疆和静县满汗王王府,书中收录了不少珍贵的历史照片,但是大家心目中还是接受不了这么一幅渥巴锡画像。所以2010年7月在和静县召开的“东归历史与文化”研讨会上安排了一项渥巴锡画像征集活动。与会的好几位蒙古族画家提交了近10幅渥巴锡画像,还有好几幅素描像。画像中的渥巴锡是一位典型的蒙古汉子。宽阔脸膛、两眼炯炯有神,是的,人们心目中的渥巴锡应该这个样子,但毕竟是艺术的创作。
在风险中性的测度下,不考虑股息与分红的情况,有风险中性概率

其中 pu、pm和 pd均属于(0,1),Δt需要满足(不考虑分红)。


从而保证在风险中性测度下此模型是可行的。
验证公式(8)的正确性从而验证所取的风险中性概率。对于一个如图2的单阶段三叉树,在风险中性测度下应该有

两边同时消去S,移项可得
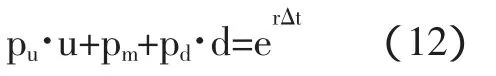
将(4)、(5)、(6)和(7)代入(11),将分母移项,可得

和等式(13)的右边比较,两者相等,则等式(10)得证,从而可以证明我们所取的概率是风险中性概率。
4 三叉树模型具体引用——经典欧式期权定价
4.1 经典欧式期权的定价 欧式期权是指赋予持有者一个在未来的某一个确定的时间以一定的价格买入或卖出标的资产的权利,其中确定的价格又叫执行价格,记为K,确定的时间又叫到期日,记为T。
同二叉树定价的方法类似,当我们建立了股票价格三叉树之后,在到期日期权的终端支付便已知,对于看涨期权,终端支付 C(S,T)=max(S-K,0);对于看跌期权,终端支付 C(S,T)=max(K-S,0)。得到终端支付以后,利用倒向归纳的方法,根据前文中风险中性测度的性质,我们可以利用以下公式给前一阶段节点的期权价格进行定价
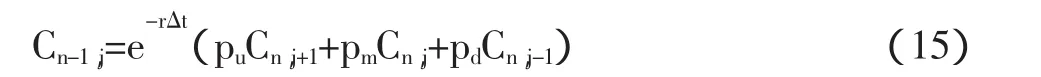
其中 Cn-1,j是第 n-1 个阶段节点 j的期权价格,Cn,j+1是从n-1个阶段节点j的在第n个阶段对应股票价格上升的期权价格,Cn,j是对应股票价格不变的期权价格,Cn,j-1是对应股票价格下降的期权价格。
这种倒向归纳的方法来源于风险中性定理并且对看涨期权和看跌期权同样适用,它可以帮助我们求出期权价格三叉树上每一个节点的期权价格,从而一直往前推出C0即起初我们想要的期权价格。
这里需要说明的是,从t到T一共经历了N期,所以对于每一次变化的时间Δt,有Δt=。
4.2 经典美式期权的定价 美式期权是指赋予持有人一个可以在到期日T之前任意时刻或者在到期日以执行价格K买入或卖出标的资产的权利。由于美式期权可以在到期日之前任意时刻实施,情况就稍微复杂了一些,如果在三叉树某一节点以执行价K实施期权获得的收益大于我们通过风险中性定价公式求得的期权价格,持有人会立即执行而非等到到期日。通过这样的分析,我们需要对倒向归纳方法进行一定的改进,从而利用改进的模型对美式期权进行定价。
美式期权终端支付的值和欧式期权一样,不同的是,对于美式期权价格树中间节点的立即支付收益,如果是看涨期权,记为;如果是看跌期权,记为,则

从而得到修正的倒向归纳公式(对于看涨期权而言)变为
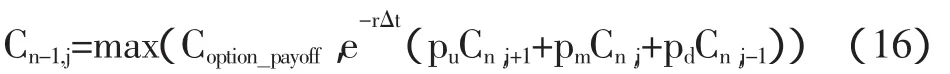
4.3 三叉树模型的收敛性 在三叉树模型中,把期数定为N,当N→∞时,可以类似于二叉树收敛性的证明,三叉树模型的随机游走过程收敛到对数几何布朗运动。众所周知,无论是二叉树模型还是三叉树模型,作为求解期权价格的数值方法,其在模拟股票价格时,理论上只有当Δt→0,股票价格才服从对数正态分布,即只有计算期数为无穷大时,二叉树或者三叉树模型计算出来的价格与BS-M公式计算得到的价格是一致的。由于三叉树的计算成本较高,我们只能取到期数为15的情况,得出的收敛性如图4所示。
由图4可知,三叉树模型在期数较少的收敛性上好于二叉树。实际上,二叉树在期数趋近于200时,价格才逐渐收敛到B-S-M解析解且波动性逐渐减弱。
5 期权价格的敏感性分析
影响期权价格的因素有很多,包括标的资产价格、执行价格、到期时间、股票波动率、无风险利率以及分红率等。我们通过MATLAB程序的作图功能分析到期时间和股票波动率对期权价格的影响。

图4 三种期权定价模型的收敛性示意
5.1 欧式看涨期权价格对到期时间T的敏感性分析 运用MATLAB编程计算后,我们可以得出欧式看涨期权价格对到期时间的关系如图5所示。

图5 欧式看涨期权价格对到期时间T的敏感性分析
由于我们计算的是欧式看涨期权,所以由图5可知,在其他条件不变的情况下(尤其是不考虑股票分红的情况),到期时间或者叫期权期限越长,欧式期权的价格越大,即欧式期权的价格随着期限的增加而增加。
5.2 欧式看跌期权价格对股票价格的波动率σ的敏感性分析 同样地,可以得到反映波动率对欧式看跌期权价格的影响,具体见图6。
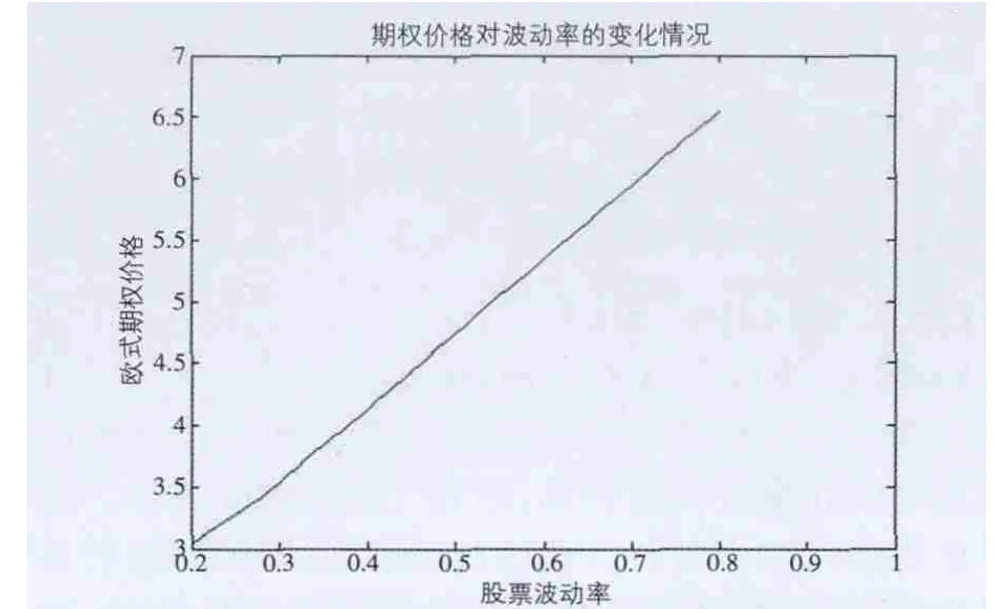
图6 欧式看跌期权价格对波动率的敏感性分析
由图6可知,期权价格随着波动率的增加而增加,这也符合人们的直观感受。粗略而言,股票价格的波动率用于衡量股票价格变动的不确定性的一个测度,当波动率增大时,股票价格上升或者下降很多的机会将会增大,对于看涨期权的持有者而言,他们可以从股票价格上升中获利,而当股票价格下跌时,其损失最多为期权费用,看跌期权也类似,所以随着波动率的增加,期权价格也会增加。
[1]Black F,Scholes M.The pricing of options and corporate liabilities[J].Journal of Political Economy,1973(81):637-659.
[2]Boyle,P.P.:Option Valuation Using a Three Jump Process[J].International Options Journal,1986,3:7-12.
[3]Cox J C,Rubinstein M.Option Markets[M].Prentice Hall,1985.
[4]COX,J.,S.ROSS and M.RUBINSTEIN,1979,Option Pricing,A Simplified Approach [J].Journal Financial Economics 7:229-263.
[5]Hull J.Options,Futures and other Derivatives,7th edition(With),Pearson Education Iadia,2010.
[6]Hull J.Option,Futures and Other Derivative Securities[M].Second Edition,Prentice Hall,1993.
[7]Rendleman,R.J.,B.J.Bartter (1979):Two-State Option Pricing.Journal of Finance[J].34:1093-1110.
[8]Steven E.Shreve著.陈启宏,陈迪华译.金融随机分析(第2卷)[M].上海:上海财经大学出版社,2008.
[9]丁正中,曾慧.实物期权的三叉树定价模型[J].统计研究,2005,11:25-28.
[10]郭宇权.金融衍生产品的数学模型[M].科学出版社,2012.
[11]郭子君,张朝清.三叉树模型下标的资产期权定价[J].华南农业大学学报,2003,2:61-65.
[12]何颖俞.美式期权的二叉树与三叉树定价模型收敛速度比较[J].杭州师范学院学报(自然科学版),2007(06).
[13]何颖俞.美式期权的三叉树定价模型[J].黑龙江大学自然科学学报,2008(01).
[14]姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2008.
[15]宋斌.期权定价实验教程[M].清华大学出版社,2014.
