基于中弧面的叶片模具型腔高质量重构方法研究

□ 卜 昆 □ 邱 飞 □ 周丽敏 □ 张定华

1.西北工业大学 现代设计与集成制造技术教育部重点实验室 西安 710072 2.中国航空工业第一集团公司 沈阳发动机设计研究所 沈阳 110015

1 概述

空心涡轮叶片是航空发动机的重要零部件，具有复杂的曲面结构，其表面的光顺性和气动性直接影响发动机的整体性能，而叶片的成型模具是影响其制造质量的关键因素。空心涡轮叶片的模具设计是一项复杂的工作，而空心涡轮叶片内、外形状的模具型腔优化设计更是其中的重点。模具型腔设计的基本原则是为模具型腔赋予适量反变形量，以抵消铸件在凝固和冷却过程中的结构变形和收缩变形。文献［1］采用了一种网格位移场反向叠加法，可以有效地使叶片的变形得到补偿。但是铸件的实际收缩是非线性的，经过反向叠加后，模具型面呈现了极不规则且表面不光顺现象，这种方法最终得到的网格离散模型在复原模具型腔时，还需要进行复杂的曲面拼接和曲面光顺。曲面拼接和光顺计算不仅费时，而且精度难以保证，很难满足使用要求。所以如何提高反变形网格模型的曲面重构质量，是模具设计过程中一个亟待解决的问题。

对网格模型的曲面重构，目前多采用数据分割技术将数据点分割为多个四边界区域，通过拟合这些四边界区域，再对相邻曲面实施连续性拼接。国内外研究学者也进行了相关研究，Ma［2］通过向基曲面投影的方法实现了散乱点的参数化。 Eck［3］和 Floater［4］通过建立一个三维三角网格向二维平面三角网格的映射，在二维平面上给出数据点的参数值，再将其映射回三维三角网格中，解决了空间三角网格的参数化问题。贺强提出了一种局部曲面逼近的网格光顺方法［5］，该方法能有效地去除模型中的噪声点，光顺的结果能很好地逼近原始模型，但是算法效率较低，而且还需要进行大量的后续处理工作。本文提出了基于叶片设计理念的型腔曲面重构方法，通过对中弧线的提取和中弧面的光顺建模，最终获得了高质量的叶片模具型腔，对涡轮叶片的模具优化设计和“精确控形”有重大意义。

2 中弧线的提取

叶片的中弧线是叶片设计的重要基准之一，它是叶片由一系列叶身截面内切圆圆心定义的一条连续曲线，合理的叶片中弧线应是高次、二阶连续的光滑曲线，中弧线的质量直接影响了叶片的造型精度和造型质量［6］。

目前常用的中弧线求解方法有解析法、等距线法、等半径法和等角度法。虞跨海提出了一种求中弧线的解析方法［7］，在这种方法中，用五次多项式表示叶盆曲线和叶背曲线，然后根据中弧线上数据点，为两条切线的交点建立一个高次方程组，以叶盆（或叶背）曲线上的一个已知切点作为起点，利用迭代的方法求解这个方程组，从而得到叶背（或叶盆）曲线上的对应切点和内切圆圆心，即中弧线上的数据点。这种方法要求先分离出叶盆曲线和叶背曲线，并且已知其方程为五次多项式曲线，而且该方法涉及到大量高次方程的迭代求解，计算量较大，因此适用面较窄。张力宁提出一种基于等距线的中弧线求法［8］，这种方法的主要步骤是：首先建立光顺的截面线模型，然后在不同的偏置距离上求截面线的精确等距线，构成等距线族，对于其中的每一条等距线求自交点，最后对于所有的自交点进行排序、插值，形成光顺的中弧线。这种方法对截面线的光顺性要求比较高，而且自交点的个数和偏置距离密切相关，自交点的个数不容易控制。因此，本文采用等半径法进行求解。

2.1 截面线的光顺处理

反变形的三角网格模型存在着局部的奇异点，使得表面出现畸变，欲获得高质量的中弧线模型，需要预先得到高质量高精度的截面线数据，所以前期需要对散乱的型腔网格数据进行预处理，预处理分以下两个步骤。

2.1.1 剔除坏点

首先对网格模型进行切片处理，获得截面线数据点。由于叶片截面线的曲率变化应该是比较平缓的，如果某一点的曲率变化比较大，认为该点是奇异点，则剔除。本文采用文献［9］中提到的圆率法来求取数据点的离散曲率。在一条封闭的轮廓线上，存在着一系列的轮廓数据点，用Pi表示，在数据点Pi处的曲率用Ki表示，Ki是用圆率法来计算的，计算公式为:

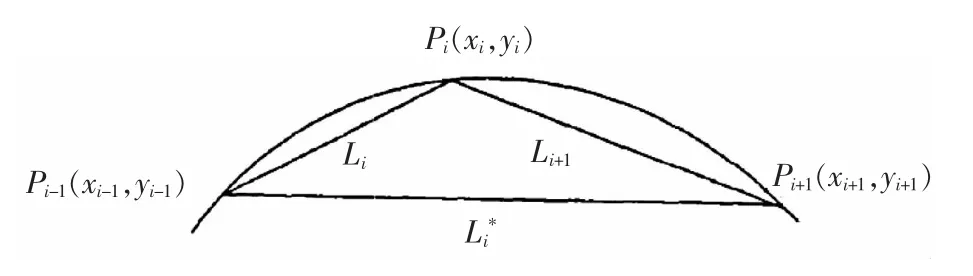
▲图1 圆曲率法示意图

圆率估算法计算简单，从离散点分布的几何位置出发，直接计算各点的离散曲率，进而判断离散点列的光顺性，挑选出坏点，这是它的优点所在。

2.1.2 最小二乘法拟合B样条曲线B样条曲线方程定义为：

式中：k 是样条曲线次数；di为控制顶点；Ni，k（u）为 k 次B 样条基函数，是由节点矢量 U=（u0，u1，u2，…，un+k+1）决定的k次分段多项式。

▲图2 拟合前曲率

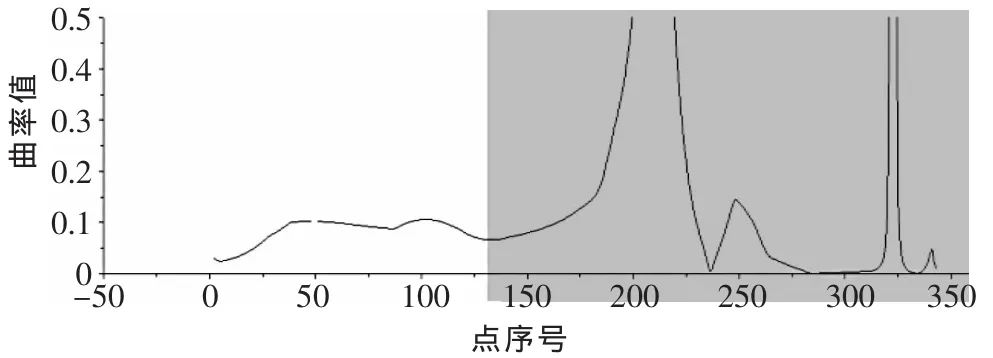
▲图3 拟合后曲率

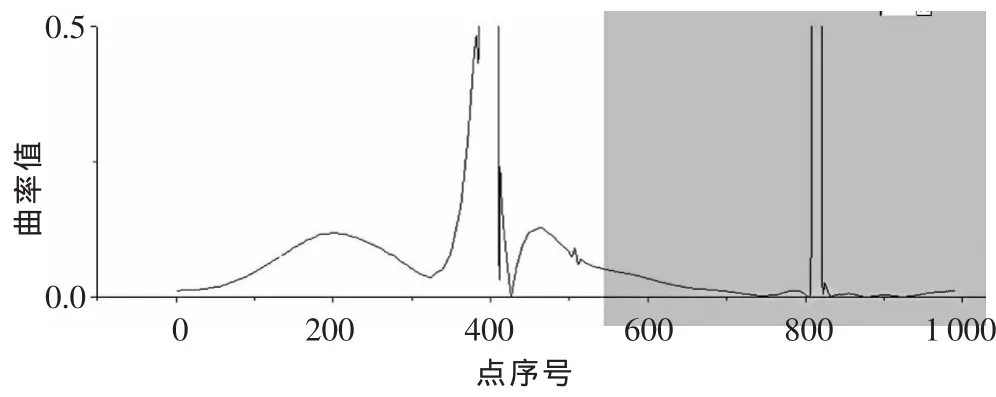
▲图4 CAD截面线曲率

对比结果表明，采用本文方法获得的截面线与叶片设计模型的截面线具有相似的曲率分布，可以达到光顺截面线的目的。

2.2 中弧线提取

对于得到的光顺截面线，按照曲率分布将叶片的截面线分成4部分，即叶盆、叶背、前缘和后缘，然后利用等半径法［11］进行中弧线的提取，提取的中弧线如图5、6 所示。

▲图5 提取中弧线数据点

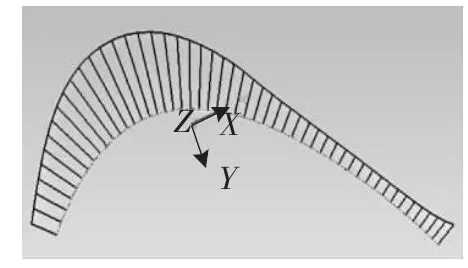
▲图6 中弧线曲率分析

由图中可以看出，采用等半径法获得的中弧线数据点分布均匀，中弧线曲率变化比较平缓，说明具有较好的光顺性。

3 中弧面建模和型腔复原

参照叶片设计理念，笔者采用以下步骤和方法进行型腔的重构，如图7所示。

▲图7 中弧面型腔重构流程

截面线的光顺处理保证了所提取中弧线的准确性和光顺性，但是多条光顺的中弧线并不能保证所获模具型腔的光顺性。本文采用中弧面的光顺建模来解决此问题，以便获得优化的中弧线数据，为型腔的光顺重构奠定基础。

3.1 中弧面的光顺建模

为了解决中弧面的曲面光顺性问题，本文采用两次拟合的方式来实现中弧面的光顺重构。对于得到的中弧线数据，首先采用插值曲线和曲面放样进行中弧面的初次拟合，拟合的曲面完全经过数据点，之后对曲面进行参数化离散，得到有序点云数据，并对点云数据进行再次拟合。再次拟合采用边界和点云拟合相结合的方法。由于非均匀有理B样条（NURBS）曲面具有很好的兼容性，所以本文采用NURBS进行中弧面的拟合。NURBS曲面数学模型可以表示为：

式中：Bi，k（u）和 Bj，l（w）是 k 次和 l次 B 样条基函数；Wi，j是控制点权因子；Vi，j控制点列。

拟合后，利用Imageware软件对中弧面进行质量分析，Imageware对曲面质量提供了全面的分析，包括视觉上的分析和定量分析。这些工具可作为一种手段来识别曲面曲率和高光效果，以发现曲面瑕疵、偏差和缺陷［12］。实践表明，采用本文方法可以得到高质量的中弧面模型，如图8、9所示。

▲图8 中弧面重构偏差分析

▲图9 中弧面重构曲率分析

通过软件分析可以看出，重构中弧面的最大偏差为0.068，其中大部分点区域的偏差在0.04以下，并且中弧面的高斯曲率变化均匀，具有较好的光顺性。

3.2 型腔重构

截取中弧面上不同高度处的中弧线，并对中弧线进行参数化离散，中弧线上的点要与厚度模型的数值一一对应，才能得到精确的叶片型线数据。所以需要依照提取厚度模型的参数序列对优化的中弧线进行离散，以便得到对应的优化中弧线数据点。

叶片造型设计过程中，一般通过包络线法获得叶片型线数据，包络线法的算法原理见文献［13］，所有这些圆心在中弧线上的内切圆的公切点形成的包络线就是叶片型线。模型重构先将不同截面数据拟合为B样条曲线，然后再由这些曲线拟合成B样条曲面来实现。针对获得的型线数据点，采用三次B样条曲线进行拟合，再用曲面放样法获得型腔曲面。

4 实例分析验证

4.1 叶片CAD（Computer-aided Design）模型的复原

▲图10 曲率图

▲图11 偏差分析

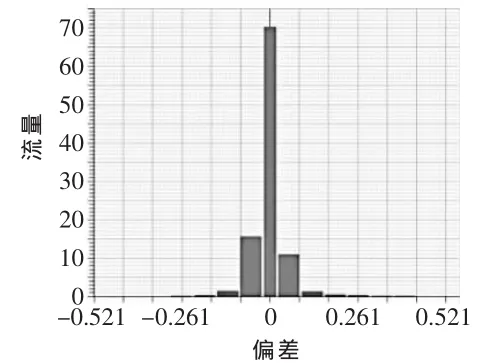
▲图12 偏差统计

▲图13 曲率分析

▲图14 偏差分析

▲图15 偏差统计

▲图16 曲率分析

▲图17 偏差分析

▲图18 偏差统计

通过Geomagic软件分析，从图10、11、12可以看出，叶片CAD模型的复原曲面具有很好的光顺性，且平均偏差为+0.024/-0.023，标准差0.041，90%以上的点的偏差在0.084以内。

4.2 反变形网格模型的型腔重构

（1）采用传统方法对网格模型进行重构得到的结果如图 13、14、15 所示。

通过Geomagic软件分析表明，传统的由点到线再到面的方法进行模具型腔的曲面重构，平均偏差为+0.011/-0.013，标准差0.026，98%以上的点重构偏差在0.1 mm以内，虽然可以保证较小的重构偏差，但是模具表面光顺性极差，不能满足工程应用需求。

（2）采用本文提出的方法对模具型腔进行重构得到的结果如图16、17、18所示。

从图16、17、18可以看出，将该方法用于反变形网格模型的曲面重构，可以达到很好的光顺效果，并且有较小的重构偏差，其中，通过Geomagic软件分析可得到平均偏差为+0.034/-0.034，标准差0.047。

对以上2个实例分析可以看出，采用文中模型重构方法，在保证重构曲面光顺性的同时，可以很好地逼近网格模型，97%以上的点重构偏差在0.1mm以内，重构误差在工程应用允许的范围内，可以达到模具型腔高质量重构的目的。

5 结束语

采用本文提出的方法对反变形网格模型进行重构，可以很好地解决模具型腔光顺问题，避免了复杂的曲面拼接过程及其带来的不光顺现象，所获得的模具型腔能够满足涡轮叶片表面光顺性和气动性要求。不足之处是该方法的智能性不足，很多地方需要人工干涉。

［1］ 王继锋.基于位移场的涡轮叶片精铸模具型腔优化设计方法研究［D］.西安：西北工业大学,2005.

［2］ Ma W,Kruth J P.NURBS Curve and Surface Fitting for Reverse Engineering ［J］.The International Journal of Advanced Manufacturing Technology,1998,14（12）:918-927.

［3］ Eck M,Hoppe H.Automatic Reconstruction of B-spline Surfaces of Arbitrary Topological Type［C］. Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques，New Orleans,USA,1996.

［4］ Floater M S.Parametrization and Smooth Approximation of Surface Triangulations ［J］.Computer Aided Design，1997,14（3）:231-250.

［5］ 贺强.基于知识的逆向工程若干关键技术研究［D］.西安:西北工业大学,2012.

［6］ 余伟巍,宋玉旺,席平.基于离散数据点的变壁厚叶身参数化设计 ［J］.北京航空航天大学学报,2008,34（11）:1319-1322.

［7］ 虞跨海.航空发动机涡轮冷却叶片多学科设计优化技术研究［D］.西安:西北工业大学,2006.

［8］ 张力宁,张定华,陈志强.基于等距线的叶片截面中弧线计算方法［J］.机械设计,2006,23（5）:39-41.

［9］ 刘晶.叶片数字化检测中的模型配准技术及应用研究［D］.西安：西北工业大学,2006.

［10］梁宏斌,孟庆鑫,李霞.非均匀有理B样条曲面五轴加工数控指令的构建与处理 ［J］.计算机集成制造系统,2009,15（5）:982-989.

［11］陈志强.基于测量数据的叶片截面特征参数提取技术研究［D］,西安:西北工业大学,2007.

［12］王征,钟绍华.用Imageware进行车身 A级曲面设计［J］.CAD/CAM 与制造业信息化,2006,（5）:58-59.

［13］窦杨青.基于中弧线的叶片模具型腔参数化优化方法［D］.西安:西北工业大学,2011.