某航空发动机附件传动系统的固有特性分析

□ 丁仁亮 □ 王三民

1.辽宁装备制造职业技术学院 沈阳 110000

2.西北工业大学 机电学院 西安 710072

附件传动系统是航空发动机的重要组成部分，其振动特性直接影响着发动机乃至整个飞机的性能。航空发动机附件传动系统是一个多级数、多分支、含非平行轴的齿轮耦合复杂转子系统，由于齿轮啮合的作用，各单根转子的振动已不再是独立的，而是彼此产生了耦合。单根转子的振动不仅与其自身的质量、刚度以及支承该转子的轴承参数有关，而且与其它转子的质量、刚度和轴承参数有关。在传动系统设计时，需要掌握结构参数对系统固有振动特性的影响规律，从而调整参数，使传动系统在工作中避免共振，保证发动机和飞机的稳定性和可靠性。本文针对某航空发动机的附件传动系统，建立其自由振动方程，分析了其固有频率和固有振型，为减振设计奠定了基础。

1 发动机附件传动系统

图1为某发动机附件传动系统的运动简图。如果将高压主动轴左侧驱动中心齿轮计算在内，该齿轮传动系统中共有15个齿轮，编号由0到14，其中有两对（4个）直齿锥齿轮，其余皆为直齿圆柱齿轮；该传动系统中共有10根转轴，编号由1到10，其中轴5为斜置（非平行）转轴，其余皆为水平转轴；系统在轴6处分成两个分支，是一个2分支系统。

在该齿轮传动系统中，轴3为发电机轴，轴7驱动滑油泵，轴8驱动燃油泵，轴10驱动供油调节器的齿轮泵。其中交流发电机的功率为5 kW，滑油泵、燃油增压泵的功率皆为0.37 kW，供油调节器齿轮泵功率为1.91 kW，主轴最大转速为51 100 r/min，巡航转速为40 880 r/min。

2 系统自由振动方程

▲图1 某发动机附件传动系统的模型

▲图2 轴单元的集总质量模型

在建立齿轮耦合复杂转子系统自由振动方程时，轴 1～轴 10 的集总质量节点数分别为 18、11、12、9、10、12、12、10、10、12，系统的总节点数为 116。10 个转子在振动方程中的排列顺序依次为轴1（1～18节点）、轴2（19～29 节点）、轴 3（30～41 节点）、轴 4（42～50 节点）、轴 5（51～60 节点）、轴 6（61～72 节点）、轴 7（73～84 节点）、轴 8（85～94 节点）、轴 9（95～104 节点）、轴 10（105～116节点）。把附件传动系统分为n个单元，即每一根轴为一个单元，各轴单元之间通过齿轮相互耦合。根据集总质量法，系统中第m个轴单元，可以等效为图2所示的集总质量模型，亦即将每个轴单元划分为许多个无质量的弹性轴段，而将转子上的分布惯性参数向轴段间的节点等效，用无弹性的惯性盘表示。

图2中：lj和dj分别为轴单元中第j个轴段的长度和直径；EIj、Kθj分别为第j个轴段的弯曲刚度和扭转刚度； mj和 Jij（i=x，y，z）分别为节点 j处惯性盘的质量和转动惯量；djik和 kjik（i，k=x，y）分别为轴承的阻尼和刚度。在局部坐标系OmXmYmZm中，第j个节点的自由振动方程可以表示为：

式中：

当第m个轴单元上的第j个节点上有齿轮 （即齿轮j）与第l个轴单元上的第i个节点上的齿轮（即齿轮 i）啮合时，式（1）可以写成：

式（2）即为第l个轴单元的自由振动方程，将所有轴单元对应的自由振动方程联立，即可得到附件传动系统的自由振动方程。

3 系统固有特性分析

依据附件传动系统的自由振动方程，求解了传动系统中所有单根转子的固有模态，表1列出了10根单转子的前六阶模态的对数衰减率及固有频率，表中δi表示第i阶模态的对数衰减率，正的表示该阶模态稳定，负的表示该阶模态发散，ωi表示第i阶模态的固有频率（已经转换为转速r/min）。

从表1中可以看出：系统有的单根转子模态中存在不稳定模态；系统的单根转子同阶模态中的固有频率，从轴1到轴10，大体上是逐渐上升的。其中以轴3为最低，轴9最高；各单根转子的固有模态大部分都集中在高频区，尤其是频率在系统工作转速以内的，数量较少，这有利于系统的稳定运行；在0到2倍系统工作转速（即81 760 r/min）范围内的模态，主要集中在轴1～轴5上，而轴6～轴10的一阶固有频率超出了这个范围。因此，在传动系统工作过程中，应该特别关注系统的前5根轴的振动特性。

由各单根转子的振型图（由于篇幅所限未列出）可以看出：由于滚动轴承不存在刚度交叉项Kxy与阻尼交叉项Cxy，单根转子又没有齿轮传动的耦合作用，其在X轴上的弯曲振动、Y轴上的弯曲振动以及扭转振动之间基本上没有发生耦合，模态的振型以某一方向上的弯曲振动或扭转振动为主；单根转子的一阶模态都是扭转振动模态 （包括刚体转动模态，即0频率模态）；前六阶固有模态多为弯曲振动模态，只有少数模态为扭转振动模态。

在考虑齿轮啮合情况下，计算了耦合系统的固有模态，表2列出了前十二阶固有频率值，图3给出了前十二阶固有振型。

▲图3 耦合系统前十二阶固有振型

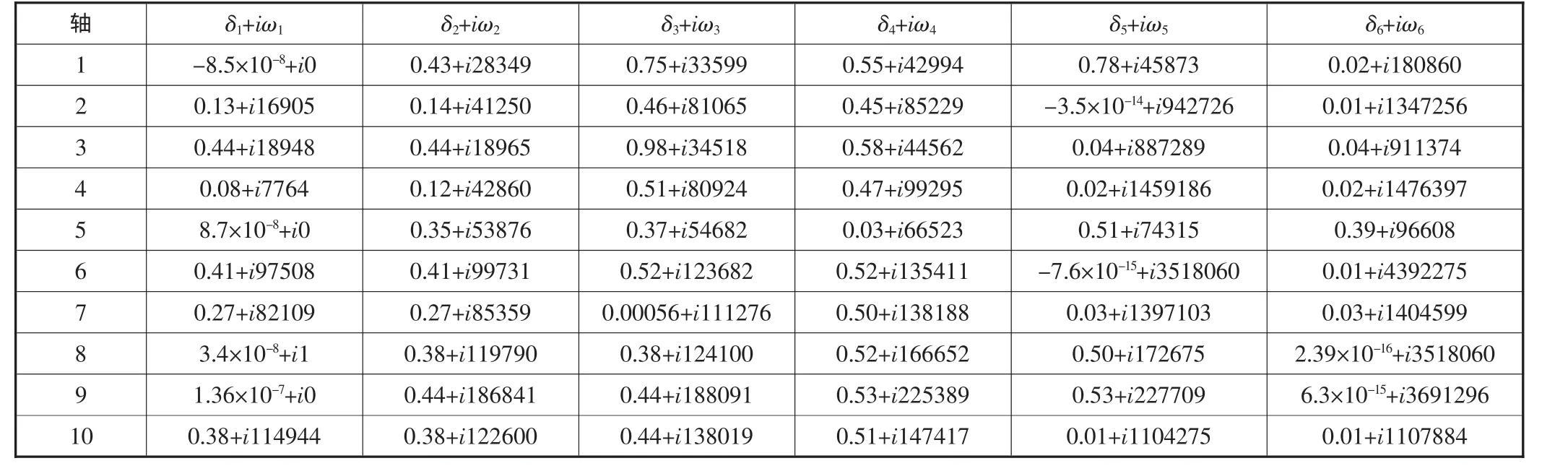
表1 单根转子前六阶模态的对数衰减率与固有频率

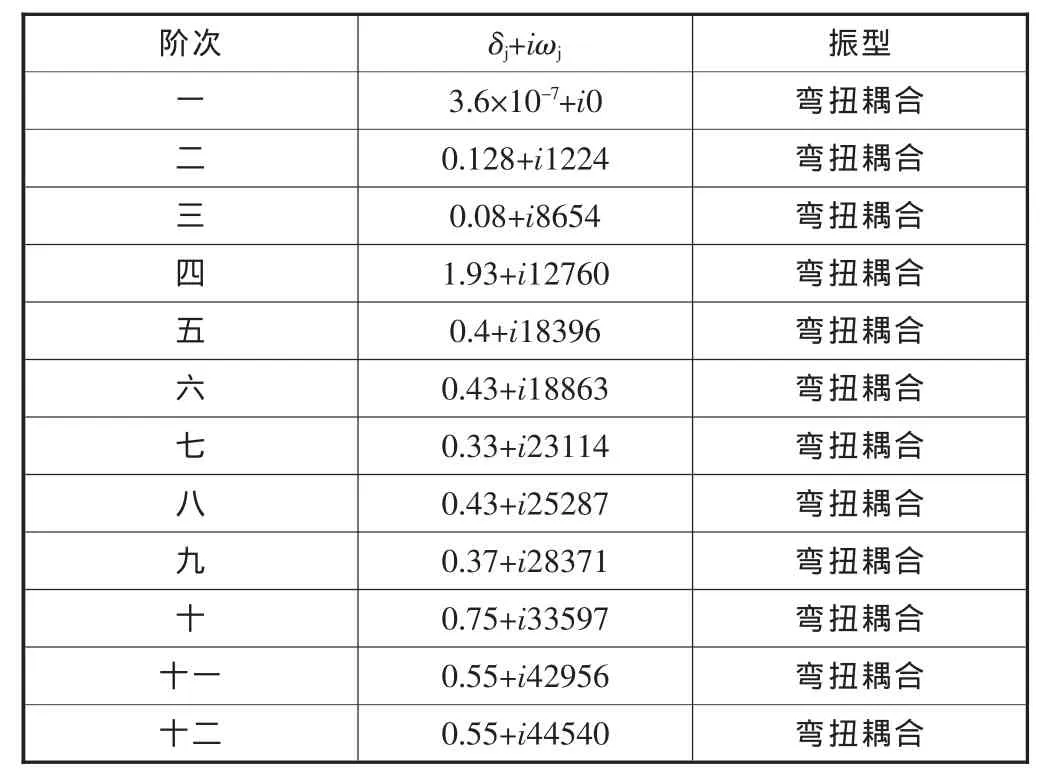
表2 耦合系统的前十二阶模态

从表2与图3中可以看出：耦合系统前十二阶模态都是稳定的，即不存在对数衰减率小于0的情况，说明系统稳定；由于各轴间的齿轮耦合作用，使耦合系统在X、Y方向上的振动与扭转振动之间发生了耦合，多数模态的振型已不再是单一的某一方向上的弯曲振动或扭转振动了；耦合系统模态分布密度较密，低频模态明显增多，因此，要小心选择工作转速，以避开共振区，提高系统的性能。

将耦合系统的固有频率及振型与单根转子 （非耦合系统）的固有频率和振型比较，很容易看出：耦合复杂转子系统中各转子对齿轮耦合作用的敏感程度各不相同。轴的尺寸相对较大、结构相对复杂的转子对齿轮耦合的作用敏感程度较低，如系统中的轴1与轴5，其保留下来的模态较多。而尺寸较小、结构较简单的转子，对齿轮耦合作用就比较敏感，如轴4、轴6与轴9等轴，保留下来的模态较少，在对系统进行设计时，更应该考虑耦合作用对其振动特性的影响。

该航空发动机附件传动系统是一个极为复杂的齿轮耦合转子系统，耦合作用非常明显，影响很大，因此派生出了大量新的耦合模态。此类模态的出现，说明按弯扭耦合力学模型设计系统的重要性，如按单根转子设计会产生大量的漏频。如果系统产生的激励恰好激起漏掉频率的共振，系统运行时会有危险的。

4 结论

（1）航空发动机附件传动系统属于齿轮耦合多转子系统，该耦合系统中包含有固有频率、衰减率与对应的单根转子基本一致的固有模态，这类模态对耦合作用不敏感。

（2）附件传动系统中包含有以某单根转子振型为主的弯扭复合振型，这是由原单根转子振型受耦合影响变化所致，其固有频率、衰减率与单根转子比较有较小变化，对齿轮耦合作用较敏感。

（3）附件传动系统中包含有耦合派生的弯扭复合振型，这种振型不易从单根转子的振型中找到对应的原形，其固有频率已不同于单根转子的值，完全是由齿轮耦合决定的，对齿轮耦合作用非常敏感。

［1］ 欧卫林，王三民，袁茹.齿轮耦合复杂转子系统弯扭耦合振动分析的轴单元法［J］.航空动力学报，2005，20（3）：197-202.

［2］ 虞烈，刘恒.轴承转子系统动力学［M］.西安:西安交通大学出版社，2001.

［3］ 张建云.齿轮传动对多平行转子-轴承系统动力学特性影响的研究［D］.西安:西安交通大学，1999.

［4］ 朱勤，谢友柏，虞烈.多根平行轴齿轮转子系统的弯曲耦合振动分析［J］.振动与冲击， 1996， 15（4）：43-47.

［5］ 夏伯乾，虞烈，谢友柏.齿轮-转子-轴承系统弯扭耦合振动模型研究［J］.西安交通大学学报， 1997， 31（12）：93-99.

［6］ Takuzo T， Shirou A.Coupled Lateral-torsional Vibration of Rotor System Train by Gears［J］.Bulletin of JSME （Japanese Society of Mechanical Engineers），1984，27:271-277.