Normal Stresses in an Ifnitite Elastic Body with a Locally Curved and Hollow Nano fiber

K.S.Alan

1　Introduction

As it had been noted in Tarnopolsky,Yu,Jigun and Polyakov(1987),Guz(1990),Kelly(1998),Akbarov and Guz(2000),Guz(2003),one of the basic reasons through which the strength of the unidirectional fibrous composites under loading along the fibers is determined principally,is the curvature of the fibers.According to the curving form,these curvatures can be classified as periodically or locally.The effective practical applications of the unidirectional fibrous composite materials,under service conditions,require intensive,systematic investigations to determine the stress deformed state in these materials,taking the curving of reinforcing fibers into account.For this purpose,in Akbarov and Guz(1985)within the framework of the piecewise homogeneous body model by the use of the three-dimensional exact equations of the theory of elasticity,the method for investigation of the mentioned stress state in the unidirectional composites was presented.This method is employed in a case where the curving of the fibers is periodic.The reviews of the results obtained by this method are detailed in Akbarov and Guz(2002).

Note that the method used in Akbarov and Guz(1985)is presented for the case where the concentration of the fibers in the composite is small enough to neglect the interactions between them.In Kosker and Akbarov(2003),the method used in Akbarov and Guz(1985)has been developed for two neighbouring periodically curved fibers and some corresponding numerical results have also been presented.In Akbarov and Kosker(2003),the method in Akbarov and Guz(1985),Akbarov and Guz(2002),Kosker and Akbarov(2003)has been developed for the geometrical nonlinear statement and numerical results for one and two neighbouring periodically curved fibers have been given.

That is all as far as the above mentioned periodical curving case is concerned.There are also few investigations,such as Djafarova(1992),Djafarova(1994),Djafarova(1995),which regard the local curving case.But these investigations have been carried out in the case where the concentration of the fibers is small enough to ignore any interaction between the fibers.Moreover,it is by the use of the linear theory of elasticity that these investigations have been carried out.According to the well-known mechanical considerations and to the results obtained in Akbarov and Kosker(2003)taking the geometrical nonlinearity into account influences significantly the values of the self-balanced stresses caused by fibers’curving.

In Kosker and Simsek(2006),Kosker and Simsek(2007),the normal stresses are analysed.The Method in Akbarov,Kosker and Simsek(2005)has been developed in Kosker and Simsek(2006)in such way as to obtain normal stress values up to the second approximation in the fiber matrix interface.In Kosker and Simsek(2007),the method has been developed for the determination of the stress distribution in the unidirectional fibrous composites with locally curved fibers is used to investigate normal stresses acting along the fibers for the case where there exists the bond covering cylinder with constant thickness between fiber and matrix materials are considered.

Alan and Akbarov(2010)developed the method for the determination of the stress distribution in the composites with unidirectional locally curved covered fibers is used for investigation of the shear stresses acting along the fibers.

The changeover from the microlevel to the nanolevel in the science of materials broke new ground in the mechanics of materials and structures.This was preceded by important events in the physics and chemistry of nanoformations,which were partially described in Guz(2006)and in Guz,Rushchitsky,Guz(2007),a basic approach to study the mechanical properties of nanocomposite materials with polymer matrix was proposed and the deformation of nanocomposites and structural members made of them.In Alan and Akbarov(2011)the normal stresses acting along the nanofiber in the nanocomposites with unidirectional locally curved covered nano fibers are considered.

Nano fibers are defined as fibers with diameters on the order of 100 nanometers.In this study,within the framework of the piecewise homogeneous body model,with the use of the three dimensional geometrically nonlinear exact equations of the theory of elasticity,the method developed for the determination of the stress distribution in the nanocomposites with unidirectional locally curved and hollow nanofibers is used for investigation of the normal stresses acting along the nanofibers.The case is considered where a single locally curved and hollow nanofiber of in finite length is located in an in finite elastic body with a low concentration of nanofibers.The interaction between the nanofibers is neglected.Futhermore,it is assumed that the body is loaded at infinity by uniformly distributed normal forces which act along the nanofibers and the crosssection of the nanofibers and normal to its axial line,is a circle of constant radius along the entire fiber length.The numerous numerical results related to stress distribution in considered body and influence of geometrical nonlinearty to this distrubition are obtained and interpreted.

2　Formulation of The problem

We consider an in finite body containing a single locally curved and hollow nanofiber with an initial local imperfection,which is illustrated schematically in Fig.1.The values related to the nanofiber are denoted by superscript(2)and those related to the matrix by superscript(1).With the middle line of the nanofiber,we associate Lagrangian rectilinearOx1x2x3and cylindricalOrθzsystem of coordinates(Fig.1).We assume that the material of the nanofiber and the matrix are homogeneous,isotropic and linear elastic.The body is compressed or stretched at infinity by uniformly distributed normal forces with intensity p acting along theOx3axis and the crosssection of the nanofiber normal to its axial line are formed by two circles of constant radius R1and R2along the entire length.Under this situation which has no motion,for the nanofiber and matrix,in the framework of the piecewise homojeneous body model with use of the three-dimensional geometrically nonlinear exact equations of the theory of elasticity of continium mechanics,we write the equilibrum equations;

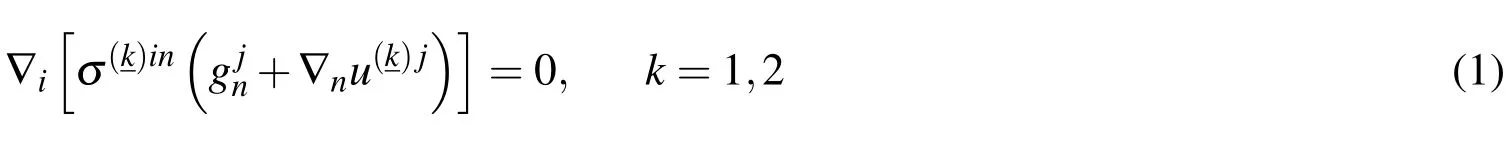
Figure 1:The geometry of material structure and chosen coordinates.

The strain-displacement relations as follows:

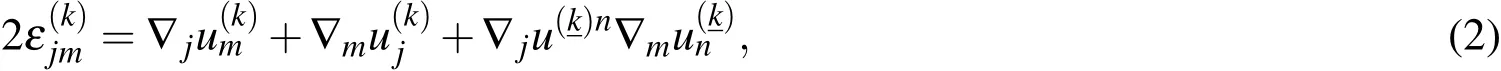
In Eqs.(1)and(2),the conventional tensor notation is used.denote the k.constant of the physical components of the stress tensors anddenotethe k.constant of the physical componenets of the strain tensors.For the detailed explanation and formulation of the equations(1),(2),and any undefined terminology and notation,we refer to Akbarov and Guz(2000).

The constitutive equations(Hooke’s Law)are as follows:

wherenjare the covariant components of the unit normal vector to the surfaces S1and S2.We assume that the matreials of the matrix and nanofiber are comparatively rigid and therefore the nonlinear terms can be neglected in the equations obtained for the zeroth approximation and the termcan be replaced by the Kronecer symbolin the first and subsequent approximatons.

For the analyzed case,the conditions are also assumed.

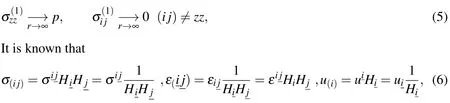
where(ij)=rr,θθ,zz,rθ,rz,zθ,(i)=r,θ,z.Hiare the Lamé coefficients,andnjare the covariant components of the unit normal to the surfaces S1and S2.σandεdenote the covariant and contravariant components of the stress tensor and the strain tensor in the sylindrical system,respectively.uianduiare the covariant and contravariant components of the displacement vector(u)in the sylindrical system.In(6)formulas are given the relationships between the physical componenets of the tensor and vectors.The physical components of this stress and strain tensor in the sylindirical system are expressed according to the covariant and contravariant components of this stress and the strain tensors.

We de fine the initial imperfection form of the nanofiber by the equation of its axial line.

Where A and L are geometrical parameter which are shown in Fig.1.εis small parameter that specie fies the curvature amplitude.Assuming that A is smalller than L,we intruduce a small parameterThe functionis the local curving form of the nanofiber.

First,using Eq.(8)and the condition for the crosssection of the nanofiber,we derive the following equation of the interface S and the components of their normal vectors in the cylindrical system of coordinatesOrθz.

wheret3is a parameter andt3∈(−∞,+∞).Using the well-known operations of differential geometry,the componentsnr,nθandnzof the unit normal vector n to the surfaces S1and S2are obtained as follows:

3　Solution Method

The considered problem is the boundary-value problem for the nonlinear partial differantial equations.For the analysis of the this problem,the boundary form perturbation method given in Akbarov and Guz(2000)are used.According to this method,the unknown values are presented as series in the small parameterε:

We expand the expression(9)-(10)as series inε;the quantities r,z,nr,nθandnzare also presented in series forms:

The expressions for the coefficients of theεkin(12)can be determined by employing some routine operations,whose details are left out here.

Substituting the expression(11)in Eq.(2)and Eq.(3)and grouping terms with identical powers,we obtain a complete system of equations for each approximation.In this case,Eq.(1)and(2)hold for the zeroth approximation,and the equations derived for the first and subsequent approximations contain the values of the previous approximations.

Now we consider the contact conditions for each approximation,which are derived from Eqs.(4).For this purpose,we substitute the expressions(11)and(12)into Eq.(4)and expand the quantitiesinvolved in eqs.(11)into Taylor series in vicinity of a point(R,θ,t3).

Then,grouping the terms with identical powers of the parameterεand taking into account the foregoing assumptions,we derive the contact conditions for each approximation:for the zeroth approximation

In Eqs.(13)and(14)the following notation is used:

The zeroth approximation.Taking into accountnr=1,nθ=0 andnz=0 in the equations(1),(2)and(3),the contact condition(4)will be provided.Therefore,the equations and the contact conditions obtained for the zeroth approximation are nonlinear equations.The zeroth approximation is the boundary-value problem for the determination of stresses and strain in the curvature-free nanofiber in our model.To the determine the zeroth approximation,we obtain the equations(16)and the contact condition(17).

In this case,an exact analytical solution is given in Akbarov and Guz(2000),Guz(2003),Akbarov and Guz(1985).According to wchich,atν(1)=ν(1),we have the following relations:

E(1),E(2)in(18)represent the elasticity modules of the matrix,nanofiber material,respectively.

The First approximation.Taking into consideration the fact that the solution ob-tained for the zeroth approximations,we assume that the materials of the matrix and nanofiber are comparatively rijid,therefore,the nonlinear trems can be neglected in the equations obtained for the first approximation and the termcan be replaced within the first and subsequent approximations.For the first approximation,we obtain the equations(19),(20)and(21).

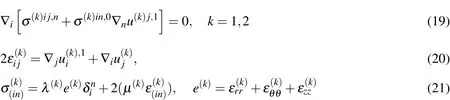
The expressions of the physical components of the equations(19)and(20)are given in Kosker(2002).

Taking into consideration the fact that the solution obtained for the zeroth approximation,other assumptions and the right-side function to be obtained for the second approximation would have values small enough to be neglected,governing equations for the first and second approximation can be de fined as follows in terms of the physical components of the tensors and vectors:

These equations coincided with the 3-dimensional linearized elasticity equations.

The mechanical and geometrical relations for the foregoing approximation are

The contact conditions for the first approximation become

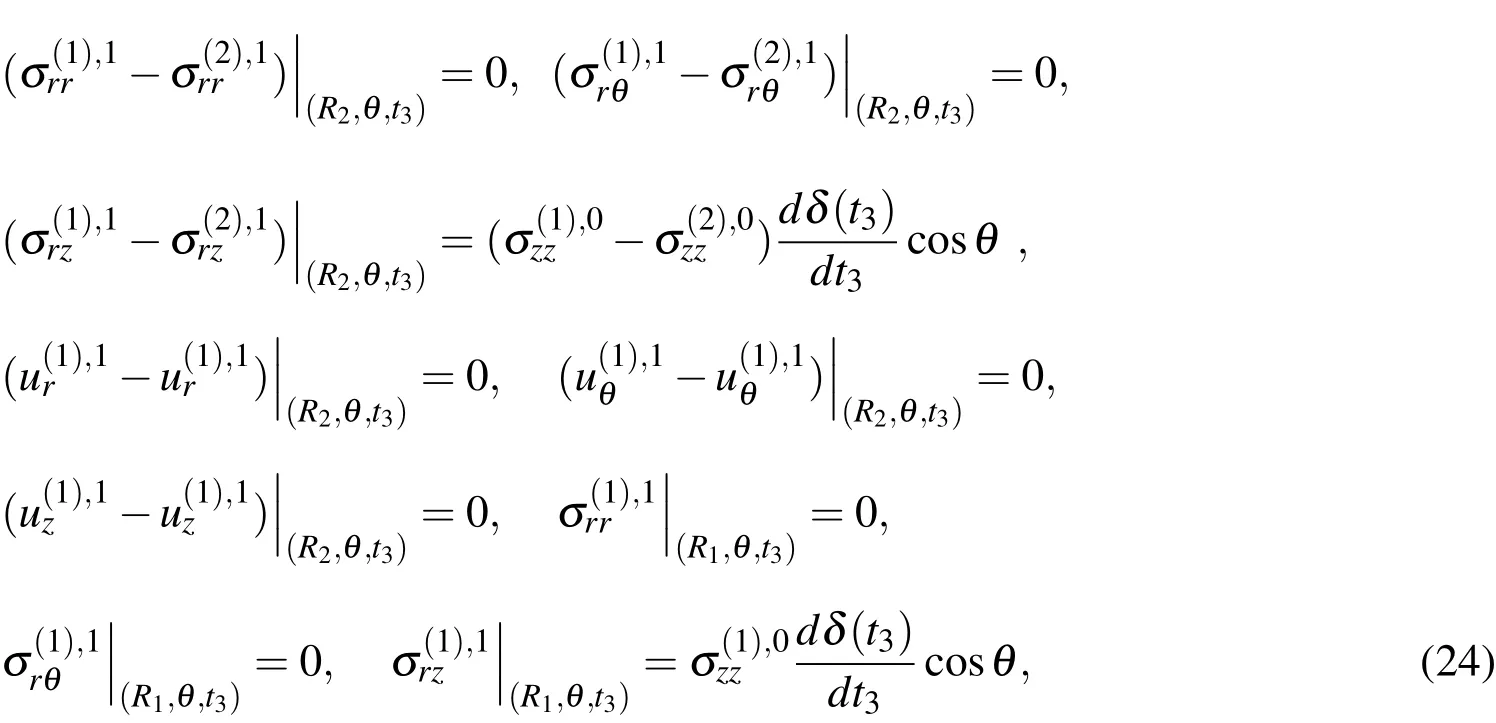
To solve the problem(22),(23),and(24),we employ the representations in Guz(1999)

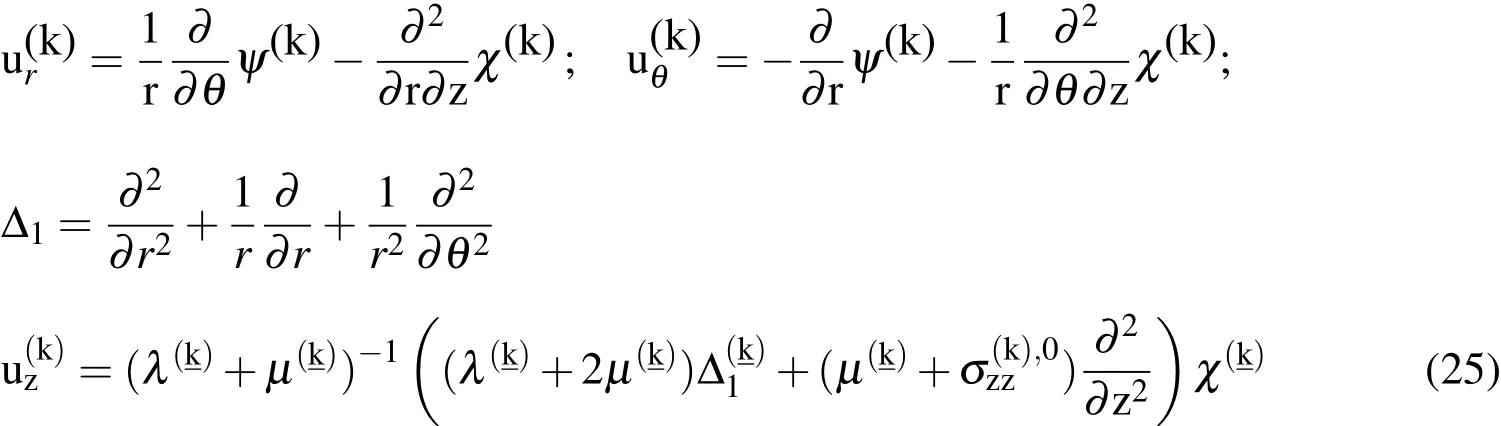
The functions ofare determined from the equations

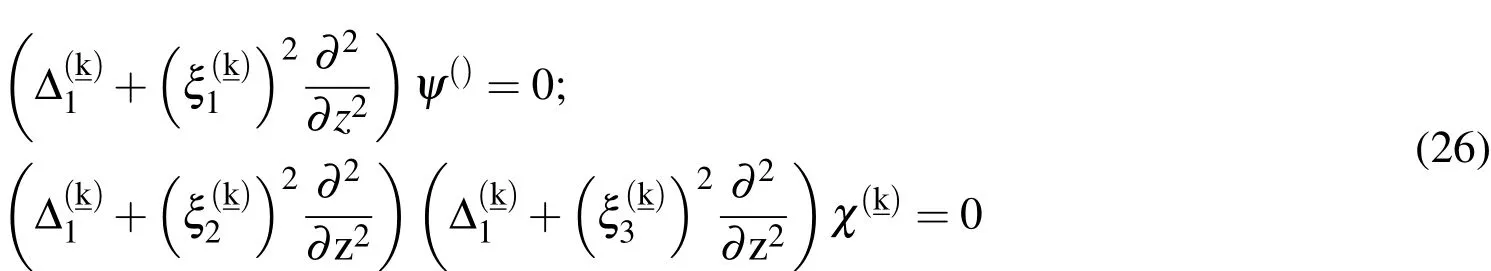
Where,(k=1,2;i=1,2,3)given in the following equations:

We apply the exponential Fourier transform with respect to z,i.e.

to the Eqs.(22)-(26).In this case,we have the governing equations as follows:

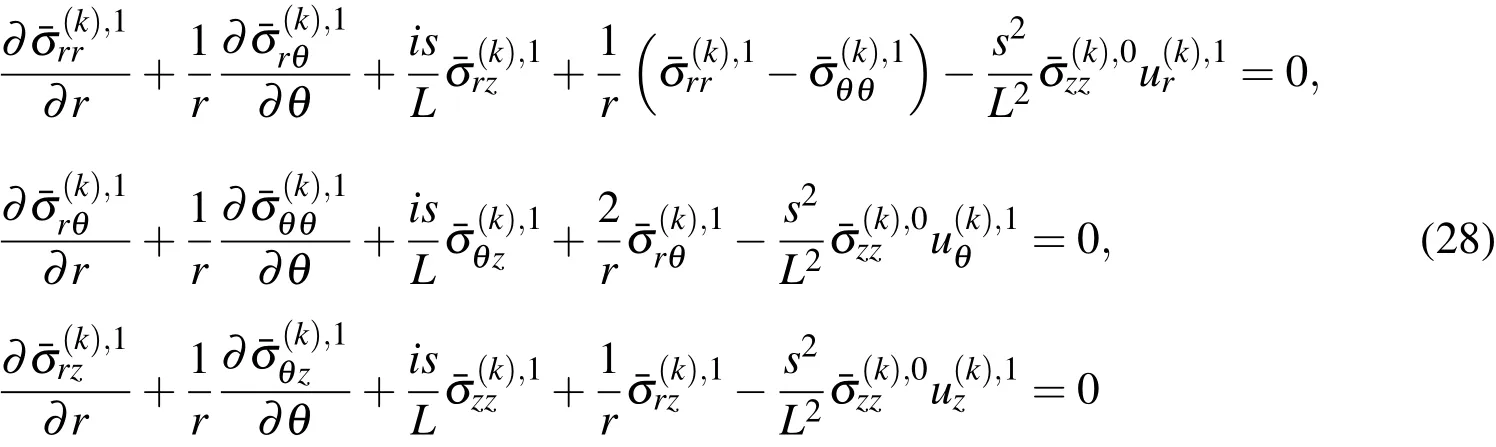
The strain are obtained as follows:

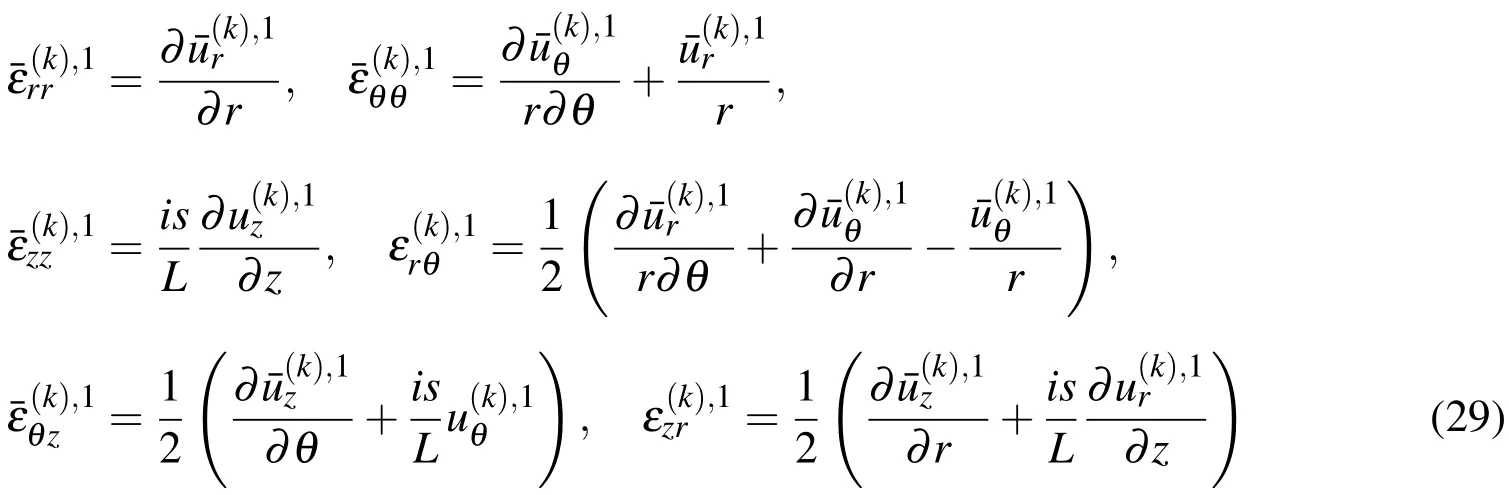
The Constutive equations are given as follows:

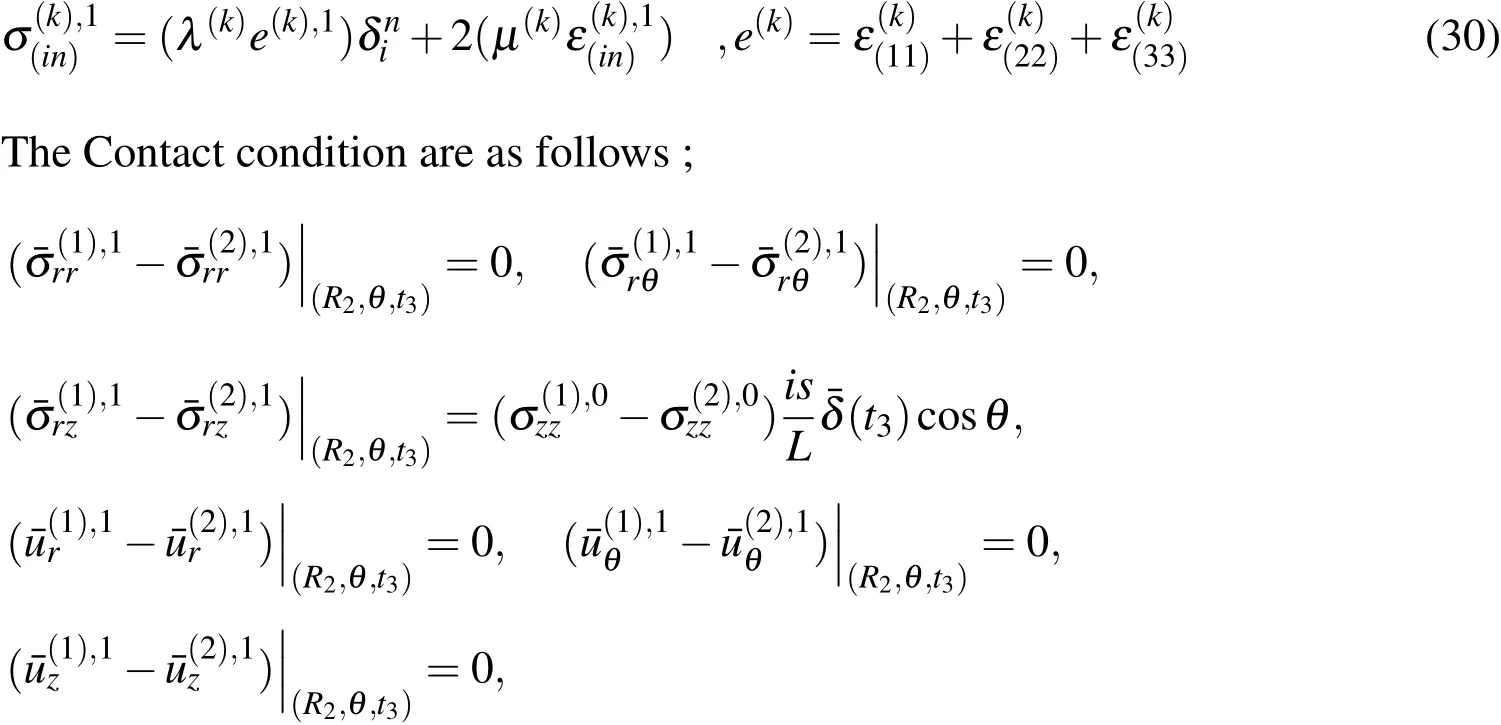
We have the expressions(25)as follows;

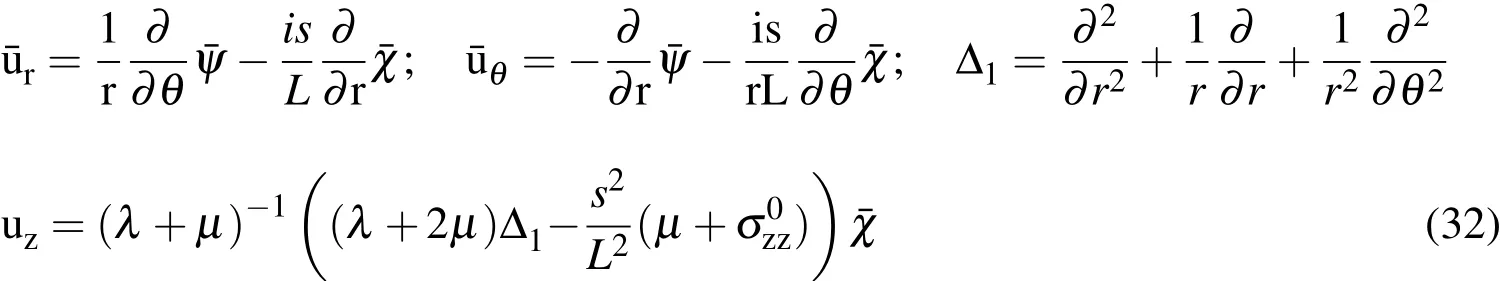
The equations(26)are as follows;

Considering the equations(28)and the contact condition(31),the equations(33)turns into the following equations

whereIn(x)are Bessel functions of a purely imaginary argument andKn(x)are the Macdonald functions.The derivatives of this function are given as follows;

The function(34)is employed in(32)and in(29)and substituted the contact condition(30);an 9x9 linear equation system is obtained which depends on the unknowns

To solving this equation system,the unknowns

Equation(4)shows that the functionδ(t3)is even,and therefore the expression(36)can be replaced with

By similar manner we obtain the expressions to calculate the other sought values.Thus,by the above-described method we determine completely the values in the first approximation.Note that the values of the second and subsequent approximations can also be determined by this method.According to the investigations analyzed in Akbarov and Guz(2004)the main effect of the fiber curving on the distribution of stresses is manifested within the framework of the first approximation.The second and subsequent approximations give only some insignificant quantitative corrections to these results.However,to determine of the values of these approximations requires some very complicated and cumbersome mathematical procedures.Taking the above stated into account the investigations in the present paper are made only within the framework of the zeroth and first approximations.

4　Numerical Results and Discussion

First,we consider some remarks on the calculation of the improved integral(37).Note that under the calculation procedure these improved integrals are replaced by the corresponding de finite ones,i.e.we use the relationThe values of N andS∗are determined from the convergence criterion of the improved integrals.Further,for the calculation of the integrals(.)dsthe Gauss integration algorithm is employed.All these procedures are made automatically in PC by using programmes written in FTN77.Thus,we consider numerical results regarding the normal stressσττ,which operate along the tangent vectorsτto surface S,which constitute the matrix and nanofiber intersection surfaces.In view of corresponding symmetry,we consider the distribution of these stresses only forIfε=0(i.e.if the curving is absent),the stressesσττcoincide withσzz.

The graphs given in Figs.2 show the relationships betweenpoint of theS1surface in tension(a)and compression(b)for various values ofαatThe intermittently lines in these figures represent the lines obtained in the problem of the single locally curved nanofiber in an in finite body given in Kosker and Simsek(2006).Here,it can be concluded that when the thickness of nanofiber material is increased,it is possible to obtain the same result as those obtained in the case of the single locally curved nanofiber in an in finite body in the same parameter values.

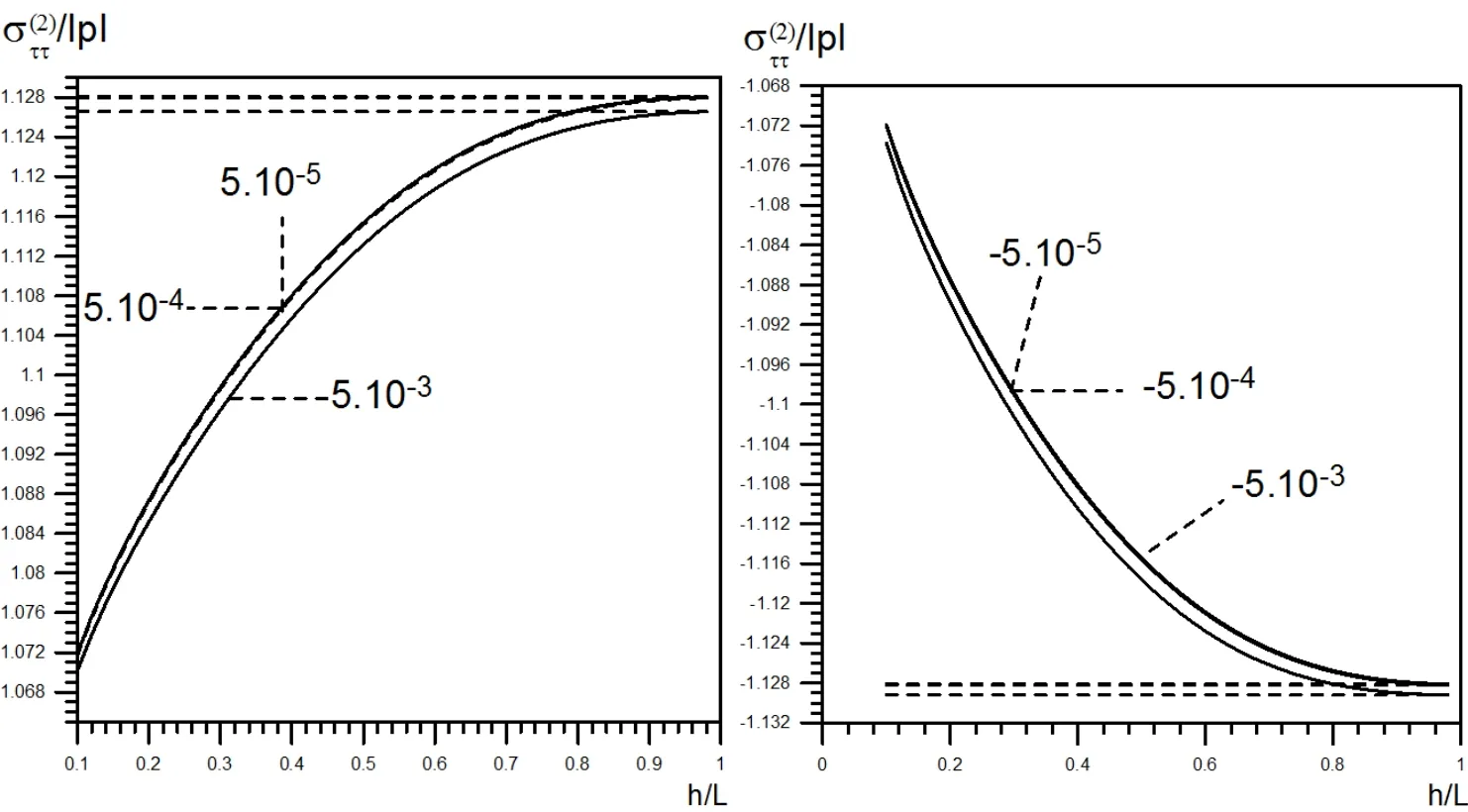
Figure 2:The relationships between σττ/|p|and h/L for values α at x3/L=1.0,and m=1(−−−)for a single locally curved nanofiber in an in finite body.

Let us consider the graphs given in Figure 3,which illustrate the distribution ofwith respect toh/Lon the surfacesS2in tension(a)and compression(b)for various values ofαandmatIt follows from the graphs that as a result of the geometrical nonlinearity,the absolute values of the stressesin compression(tension)increase(decrease)monotonically with absolute values ofα.Note that under compression of the considered in finite body we assume that the selected values ofαare smaller than those of critical valuesαcr,which correspond to the micro-buckling of the fiber in the matrix in Guz(1990).

The same figures show also the influence of the parameter m on the distribution of the normal stresses.According to the graphs in Figure 3,absolute maximal values of the normal stressesincrease monotonically with m.

In.Fig.4 and 5,relationships betweenand x3/L on the surfacesS1and surfacesS2in tension(a)and compression(b)are shown for various values ofαat h/L=0.5 value.It follows from the graphs that as a result of the geometrical nonlinearity the absolute values of the stressesincrease(decrease)monotonically with absolute values ofαunder compression(tension).Note that under compression of the considered in finite body we assume that the selected values ofαare smaller than those ofαcr.which correspond to the micro-buckling of the fiber in the matrix in Guz(1990).

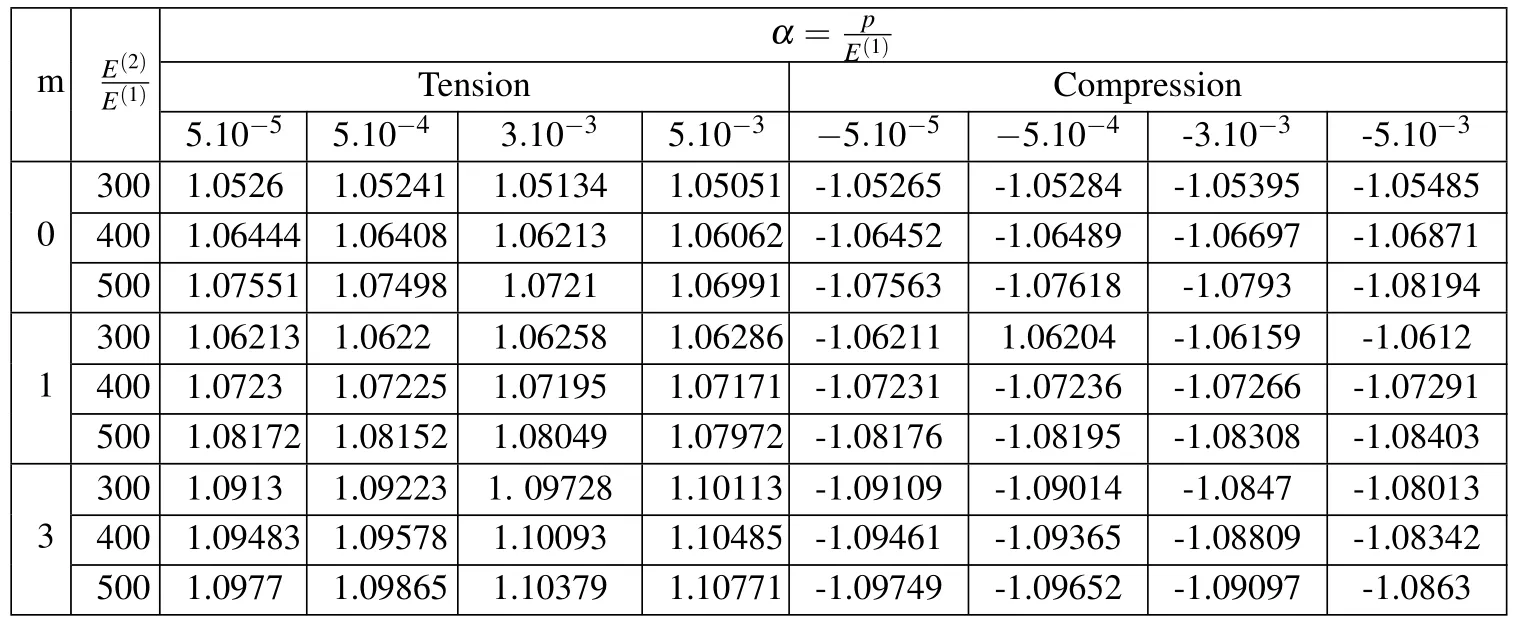
Table 1 shows the values offor variousm andα.In this case the values ofare calculated underκ=0.25,=1.0 form=0,1 and 3 respectively.The table shows thatnormal stresses increase withand m.We assume thatαis smaller than its critical valuesαcrcorresponding to microbukling of the fiber in the matrix in Guz(1990).

?

5　Conclusion

Figure 3:Distribution of the with respect to h/L for various where E(2)/E(1)=300,ε=0.07 and κ =0.3,under m=0;m=1;m=3.

Figure 4:Distribution of the with respect to x3/L for variouswhere E(2)/E(1)=300,ε=0.07 and κ =0.3,under m=0;m=1;m=3.

Figure 5:Distribution of the with respect to for variouswhere E(2)/E(1)=300,ε=0.07 and κ =0.3,under m=0;m=1;m=3.

In the present paper in the framework of the piecewise homogeneous body model with the use of the three-dimensional geometrically nonlinear exact equations of the theory of elasticity,the method is developed for the determination of the stress-strain state in the nanocomposites with unidirectional locally curved and hollow nanofibers is used for investigation of the normal stresses acting along the nanofibers.The case is considered where a locally curved and hollow nanofiber of in finite length is located in an in finite elastic body with a low concentration of nanofibers.The interaction between the nanofibers is neglected.

The numerical results related normal stresses,which act on the interface,are given.From the analyses of the numerical results are derived the following conclusions:

1.when the thickness between the hollow and nanofiber goes to 0 as a limit,it was obtained the same normal stresses values in the locally curved nanofiber in an nanocomposite material in same parameter values.

2.As a result of the geometrical nonlinearity the absolute values of normal stresses,increase(decrease)in compression(tension)with|α|.

3.The absolute maximum values of the considered stresses increase with

monotically with m.

4.An increase inresults in an increase in the absolute values of the normal stresses on the Hollow and nanofiber interface.

The locally curvature of nanofiber is one of characteristics of nanocomposites as noted in Guz,Rushchitsky and Guz(2007),Guz and Chekhov(2007),Xiao,Zhang,Zarudi(2007).These results are also important for estimating the adhesion stress between the nanofibers and a polymer matrix.In this case,it is necessary to take into account the restrictions noted in Guz,Rushchitsky and Guz(2007).

The numerical results obtained agree with well-known mechanical consideration and,in some particular cases,coincide with known results.

Akbarov,S.D.;Guz,A.N.(1985):Method of Solving Problems in the Mechanics of Fiber Composites With Curved Structures.Soviet Applied Mechanics,pp.777-785.

Akbarov,S.D.;Guz,A.N.(2000):Mechanics of Curved Composites.Kluwer Academic Publishers,Dordrecht,The Netherlands,464p.

Akbarov,S.D.;Guz,A.N.(2002):Mechanics of curved composites(piecewise homogenous body model).Int.Appl.Mech.,vol.38,no.12,pp.1415-1439.

Akbarov,S.D.;Kosker,R.(2003):On a stress analysis in the in finite elastic body with two neighbouring curved fibers.Composites Part B:Engineering,vol.34 no.2,pp.143-150.

Akbarov,S.D.;Kosker,R.;Simsek,K.(2005):Stress distribution in an in finite elastic body with a locally curved fiber in a geometrically nonlinear statement.Mechanics of Composite Materials,vol.41,no.4,pp.291-302.

Alan,K.S.;Akbarov,S.D.(2010):The Self-Balanced Shear Stresses in The Elastic Body with a Locally Curved Covered Fiber.Adv.Mec.Eng.,vol.2010,pp.1-14.

Alan,K.S.;Akbarov,S.D.(2011):Stress Analyses in an In finite Elastic Body with a Locally Curved Covered Nano fiber.Mechanics of Composite Materials.Issue 3,vol.47,pp.343–358.

Djafarova,E.K.(1992):On the solution method of the stress-strain state problems in the fibrous composites with locally curving structures.Tr.Nauch.Konf.Molod.Uchyon.In-ta Mekhan.AN Ukr.,Kiew,Part I,pp.39-44.

Djafarova,E.K.(1994):Distribution of self-equilibrated stresses in fibrous composite materials with local curving in the structures.Dep.In VINIT.,N 2166-B94–34p.

Djafarova,E.K.(1995):Stress state in composite materials with local curving fibers.Dissertation for the degree of Candidate of Physico-Mathematical Sciences.Institude of Mathematics and Mechanics of National Academy of Science of Azerbaijan,Baku.

Guz,A.N.(1990):Failure mechanics of composite materials in compression.Kiev:Naukova Dumka Russia,630p.

Guz,A.N.(1999):Fundamentals of the Three-Dimensional Theory of Stability of Deformable Bodies.Springer.Newyork,NY.

Guz,A.N.(2003):On one two-level model in the mesomechanics of compression fracture of Cracked Composites.Int.Appl.Mech.,vol.39,no.3,pp.274-285.

Guz,A.N.(2006):The Three-Dimensional Theory of Stability of a CarbonNanotube.Int.Appl.Mech.,vol.42,no.1,pp.19-31.

Guz,A.N.;Rushchitsky,J.J.;Guz,I.N.(2007):Establishing fundamentals of the Mechanics of Nanocomposites.Int.Appl.Mech.,vol.43,no.3,pp.247-269.

Guz,A.N.;Chekhov,V.N.(2007):Problems of folding in the earth.Int.Appl.Mech.,vol.43,no.2.

Kelly,A.(1998):Composite Materials:impediments do wider use and some suggestions to overcome these.In Proceeding Book(ECCM-8),Napoles-Italy,vol.I,pp.15-18.

Kosker,R.(2002):Some Problems abaut internal stability loss and stress distribution in an elastic and viscoelastic unidirected fibrous composites.The Phd.Thesis,pp.138.

Kosker,R.;Akbarov,S.D.(2003):In fluence of the interaction between two neighbouring periodically curved fibers on the stress distribution in a composite material.Mechanics of Composite Materials,vol.39,no.2,pp.165-176.

Kosker,R.;Simsek,K.(2006):On the normal stresses in the elastic body with a locally curved fiber under geometric nonlinear statement.Sigma,Journal of Engineering and Natural Sciences,vol.3,pp.97-98.

Kosker,R.;Simsek,K.(2007):Normal Stresses in the elastic body with a locally curved covered fiber.Sigma,Journal of Engineering and Natural Sciences,vol.3,pp.223-235.

Tarnopolsky,Yu.M.;Jigun I.G.;Polyakov,V.A.(1987):Spatially-reinforced composite materials.Handbook,Mashinostroyenia,Moscow,Russia.

Xiao,K.Q.;Zhang,L.C.;Zarudi,I.(2007):Mechanical and rheological properties of carbon nanotube-reinforced polyethylene composites.Compos.Sci.,Technol.,vol.67,no.2,pp.177-182.