现浇板框架抗震性能的试验研究及理论分析

宁 宁，屈文俊，朱 鹏

（同济大学 土木工程学院，上海200092）

实际框架结构的抗震性能、破坏过程和受力机制与不考虑现浇板作用的空框架有所差异，为此，国内外学者开展了一系列试验与理论研究［1-5］.研究表明，考虑现浇板作用后，结构梁端抗弯承载力增加，破坏模式发生改变，结构产生“强梁弱柱”的破坏形态；现浇板对结构抗震性能的影响可通过计算有效翼缘宽度来反映，并建议了现浇板受拉有效翼缘宽度的取值范围［2-3，6-10］.

有关研究主要集中在有限元模拟、试验和计算模型的推导，而试验主要集中在节点、一榀连续框架的抗震性能，针对空间框架的抗震试验很少.单个节点和平面框架未能有效考虑结构的空间作用，此时现浇板和直交梁容易发生平面内弯曲［3］，这与实际结构受力有所差别，而空间框架与实际结构相似，可以反映结构真实的抗震性能.本文基于现浇板空间框架的低周反复试验，研究了现浇板纵筋应变分布及现浇板参与梁端弯矩情况；提出了现浇板受力拉压杆模型，用以计算现浇板受拉有翼缘宽度，反映现浇板参与实际受力的情况.

1 试验设计

1.1 试验材料

试验采用PO42.5普通硅酸盐水泥，JC-3型缓凝高效减水剂，砂为普通中砂，天然粗骨料为碎石，连续级配，拌合水为自来水.模型分两批次浇筑，一层与二层混凝土浇筑后28d力学性能见表1.

柱纵向受力钢筋采用HRB335级钢筋，梁、板受力钢筋与箍筋采用HPB235级钢筋，其中柱纵筋直径为10mm，梁纵筋直径为8mm，现浇板钢筋及箍筋直径为6mm，实测钢筋的屈服强度、极限强度与弹性模量如表2所示.

表1 混凝土力学性能Tab.1 The properties of concrete

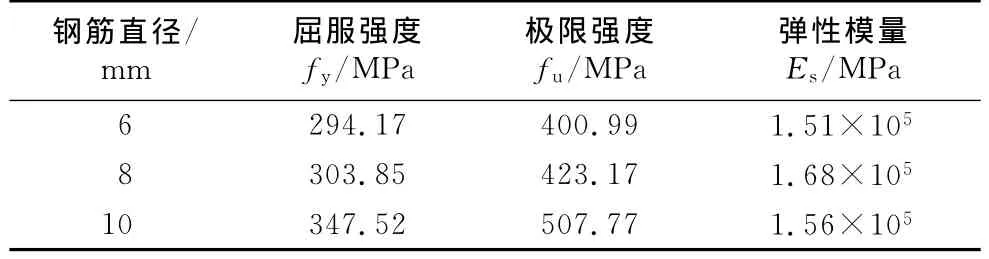
表2 钢筋力学性能Tab.2 The properties of steel

1.2 模型设计

本次试验共计两个模型：未设现浇板的空间框架KJ-1与有现浇板的空间框架KJ-2.框架根据《混凝土结构设计规范》进行设计，缩尺比例为1∶2.5.两个模型外型尺寸及构件尺寸均相同，均采用2跨×1跨“日”字形两层空间框架结构.模型长4m，宽1.6m，高2.88m.长边方向长跨2.4m，短跨1.6 m；短边方向横跨1.6m.柱尺寸160mm×160mm，梁尺寸100mm×200mm，现浇板厚50mm，基础底座尺寸300mm×400mm.两模型的梁、柱配筋均相同，模型尺寸及配筋详图如图1所示.

1.3 试验方法和加载制度

本试验在同济大学建筑结构试验室进行.参考《建筑抗震试验方法规程》（JG101—96）的规定，本次试验采用拟静力试验方案.为防止模型发生平面外扭转，采用两个油压千斤顶在框架顶层同步施加水平低周反复荷载，试验加载详图如图2所示.为保证KJ-1和KJ-2质量相同，试验前在KJ-1各个梁上进行堆载以模拟现浇板重量.

试验采用位移控制加载，正式试验前采用±2 mm（0.05%层间侧移角）预加载，以测试应变片等仪器是否正常工作.

正式试验时位移加载方式为：±3mm（0.1%）→±6mm（0.2%）→±9mm（0.3%）→±12mm（0.4%）→±17mm（0.6%）→±23mm（0.8%）→±29mm（1.0%）→±36mm（1.3%）→±43mm（1.5%）→±58mm（2.0%）→±72mm（2.5%）→±86mm（3.0%）→±101mm（3.5%）→±110mm（4.0%）→±120mm（4.2%），每级位移循环3次.试验过程中加卸载速度保持匀速.

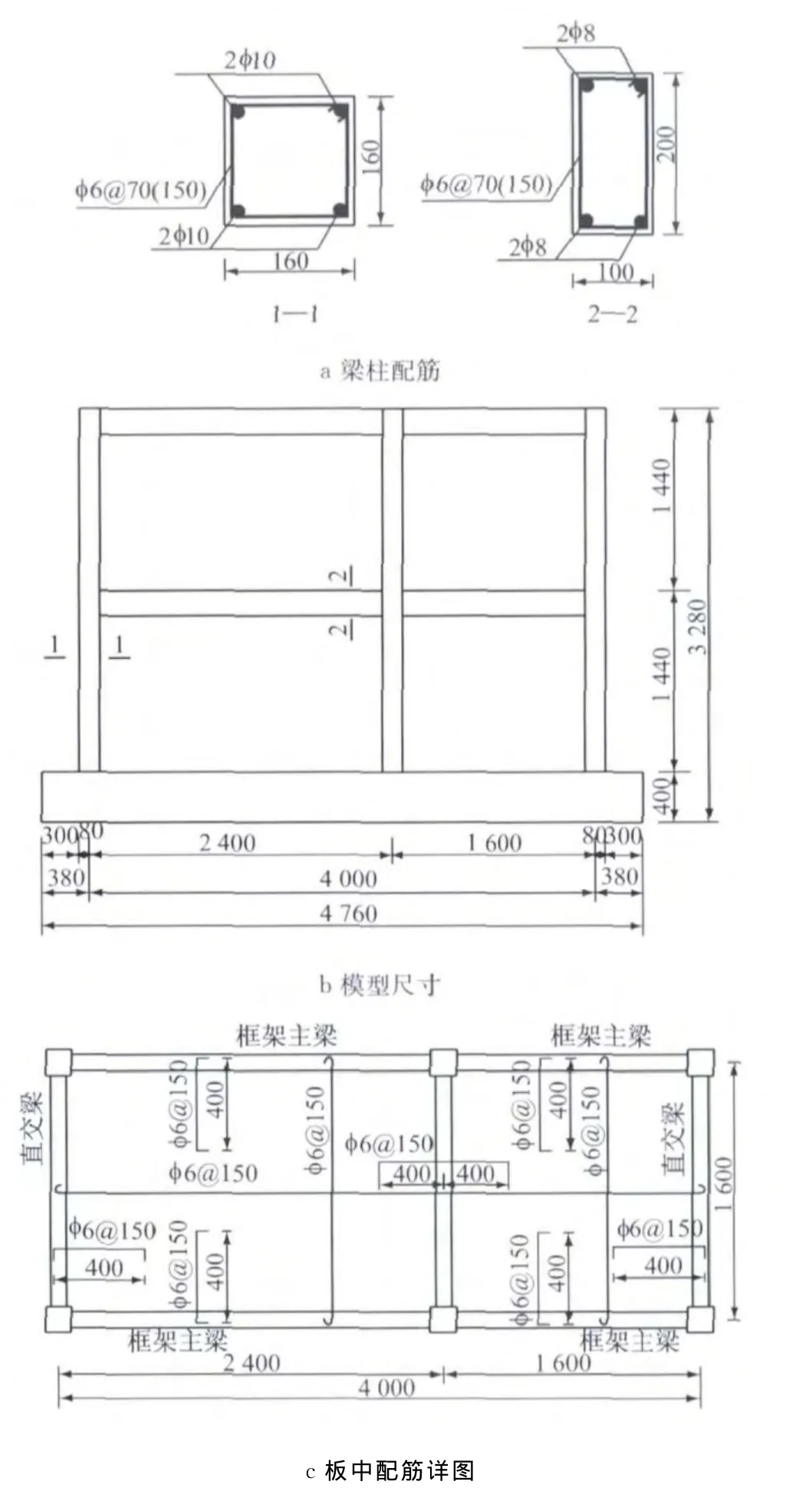
图1 模型尺寸和配筋 （单位：mm）Fig.1 The design of specimens（unit：mm）

2 抗震性能分析

2.1 试验现象

KJ-1模型在加载初期 （±3mm）未出现开裂现象，随着加载的进行，当达到±6mm时，在一层梁柱端部受拉区混凝土开裂，裂缝宽度约为0.2mm.此时模型滞回曲线包围面积狭小，模型基本处于弹性工作阶段.随着水平位移的不断增加，梁、柱端混凝土不断出现新的裂缝，裂缝宽度逐渐增大，开裂现象明显.层间侧移角为1.5%～2.0% （±43mm→±58mm）时，裂缝基本出齐，并不断扩大.±58mm时可听到较清晰的混凝土破碎声音，一层边柱核心区出现斜裂缝.当到达加载阶段末期，一层角节点混凝土保护层脱落，柱脚混凝土受压破坏，钢筋屈服.KJ-1模型一层各个梁端钢筋全部屈服，混凝土开裂较大，呈明显的“强柱弱梁”破坏机制.

KJ-2模型在试验初期混凝土的开裂、扩展过程与KJ-1模型相似，但梁端的裂缝明显减少，柱端裂缝明显增多，且现浇板中出现平行于短跨方向的细裂缝与斜裂缝.随着加载的进行，当加载进行到±43 mm→±58mm时，梁、柱裂缝基本出齐，节点核心区同时出现了斜裂缝.在±58mm时可听到较清晰的混凝土破碎声音，现浇板已有裂缝加宽并不断出现新裂缝 （图3），直交梁梁端扭转裂缝明显 （图4）.最终，模型一层柱脚混凝土受压竖向开裂，钢筋屈服，一层角节点侧面混凝土保护层脱落.对比KJ-1与KJ-2模型的最终破坏形态，KJ-2最终破坏时二层中柱底部钢筋屈服，混凝土开裂较大，且边节点两侧梁端裂缝较KJ-1少.KJ-2呈“强梁弱柱”的破坏机制.

图2 模型加载装置Fig.2 The loading setup

两框架加载全过程中，平面外位移计读数均很小，表明框架扭转现象不明显，可以忽略.

加拿大哥伦比亚省吉隆纳市的奥卡那根中学在2012-2013学年进行了＂翻转课堂＂教学实践，这种新式教学模式一经使用便受到了家长和学生的极大支持。为了提高实验效果，同时方便教师之间进行交流，该校还专门成立了＂翻转课堂＂教学网站为教师提供服务。在澳大利亚，昆士兰州立高中和昆士杰大学针对＂什么是翻转课堂＂、＂为什么要采取这种教学形式＂和＂如何开展使用这种教学模式＂等问题进行了深入研讨，研究结果显示：翻转课堂能为学生提供充裕的时间发展高级思维，其结果能促进学生转向主动学习。

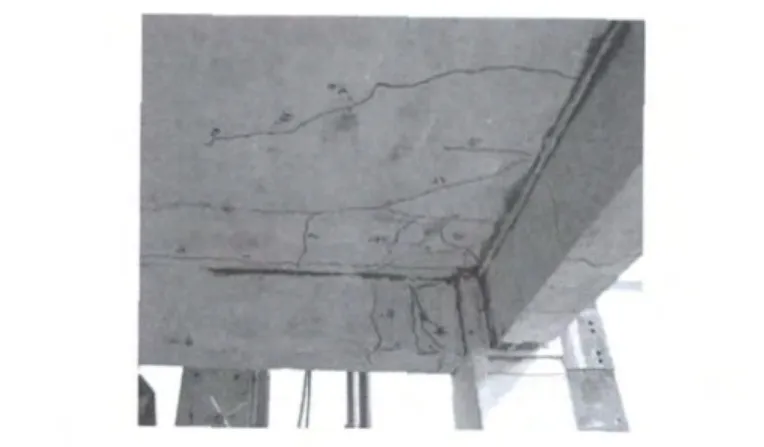
图3 现浇板裂缝Fig.3 The crack of slab

图4 KJ-2直交梁扭转裂缝Fig.4 The torsion crack of KJ-2transverse beam

2.2 滞回曲线

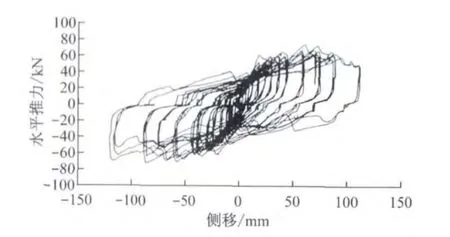
图5 KJ-1的滞回曲线Fig.5 The hysteresis loop of KJ-1

图6 KJ-2的滞回曲线Fig.6 The hysteresis loop of KJ-2

滞回曲线反映了在低周反复试验中，水平作用力与侧移之间的关系，是进行抗震设计的重要依据.KJ-1，KJ-2在低周反复荷载作用下的水平推力-侧移（P-Δ）滞回曲线分别如图5、图6所示，对比两图可得出：

在试验加载初期 （±6mm），模型滞回环包围面积狭小，力和位移基本上呈直线变化，刚度退化不明显；结构进入弹塑性阶段后，滞回曲线呈弓形，曲线趋向丰满，耗能能力加强.对比现浇板作用对滞回曲线的影响：两框架滞回曲线的形状基本相似，KJ-2滞回环所包围面积较KJ-1大，表明KJ-2较KJ-1耗能大；随着循环次数的加大，模型耗能能力不断增强，在每一级位移阶段，后一次循环都较前一次的荷载低，说明刚度和强度由于损伤累积的影响而不断下降.

2.3 特征荷载与特征位移

模型的屈服荷载Py与峰值荷载Pmax见表3.其中模型屈服荷载的大小按能量等值法来确定.从表3中可以得出，KJ-2的屈服荷载较KJ-1提高13.7%，峰值荷载提高15.2%，表明现浇板的存在较明显地提高了框架的承载力.模型的屈服位移Δy和峰值位移Δmax如表3所示.KJ-2的屈服位移较KJ-1降低16.7%，峰值位移较KJ-1降低2.2%.采用位移延性系数μ=Δmax／Δy与极限层间侧移角Rmax=Δmax／H来反映结构延性的大小 （H为模型高度）.计算结果表明，两框架均具有良好的延性；两框架的极限层间侧移角分别为1／35和1／36，说明在峰值点KJ-1的变形能力略优于KJ-2，框架结构具有良好的变形能力.

表3 特征位移与特征荷载Tab.3 The characteristic displacement and load

3 试验数据分析

3.1 现浇板钢筋应变分布

框架在承受水平荷载时，现浇板处于受拉或受压状态.现浇板受拉时，板中钢筋受拉，框架梁端弯矩将增大［9］.为研究现浇板对梁端弯矩的影响，提取框架一层现浇板中板底和板面纵向钢筋应变在不同位移角下的变化趋势，如图7、图8所示.

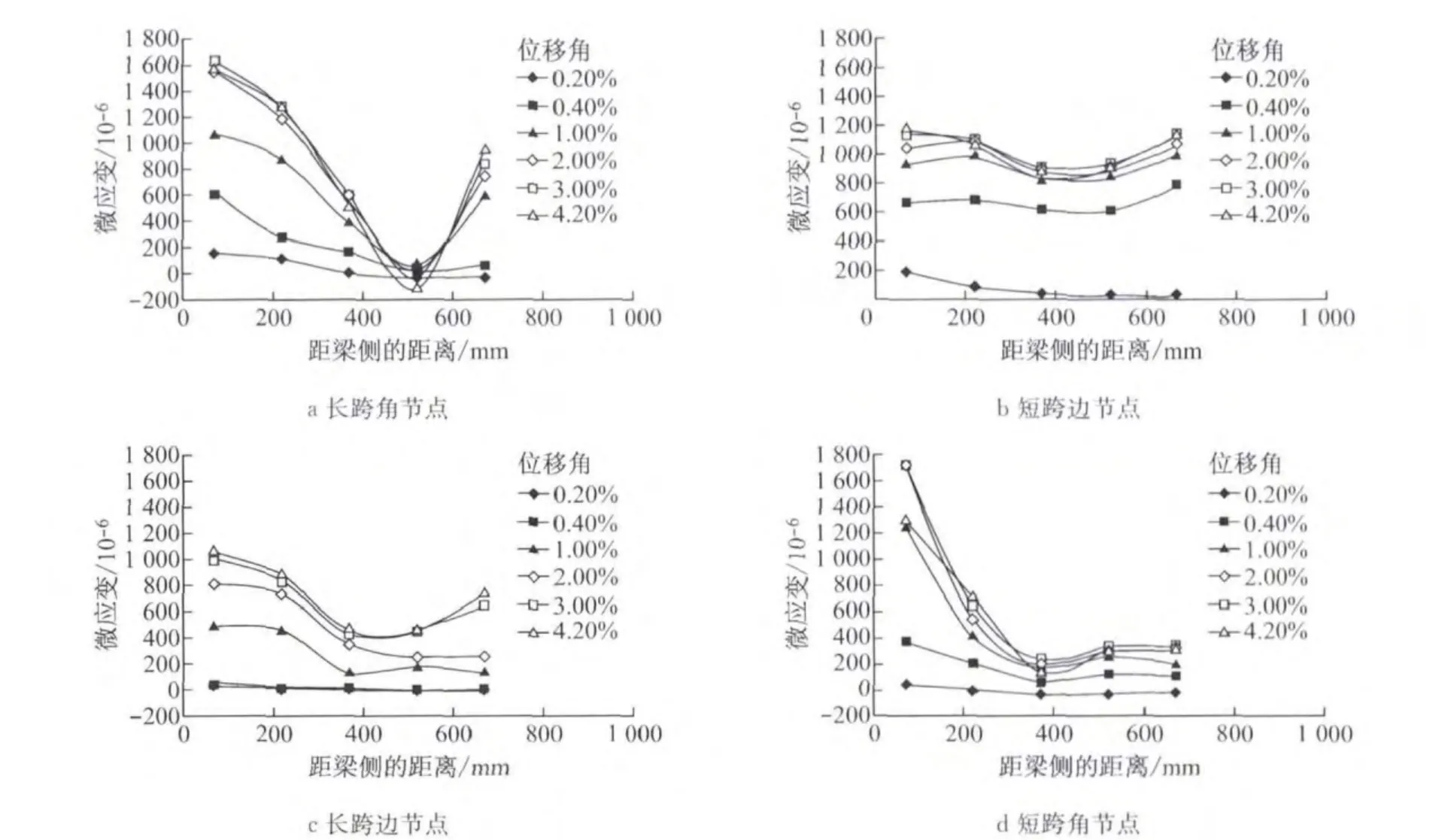
图7 一层现浇板受拉时钢筋应变（板底钢筋）Fig.7 The strain of slab longitudinal reinforcement in slab-in-tension case（bottom layer）

从图7中可以得出，在加载初期（3mm→9 mm），现浇板板底钢筋应变一般很小，现浇板参与受力作用不明显.相比较而言，靠近梁侧的现浇板钢筋应变大，随着距梁侧距离的增大应变逐渐减小，这也反映出剪力滞后的效应.随着侧向位移的增大，现浇板钢筋应变逐渐增大，表明此时现浇板逐步参与框架结构受力，结构受力状态发生变化.极限状态时短跨角节点靠近梁侧的现浇板钢筋应变略大于长跨角节点处的钢筋应变.而边节点的现浇板钢筋应变变化较角节点处的平缓.

从图8中可以得出，板面钢筋应变分布形状较板底钢筋略有不同，且其值较大，因此不可忽略板面钢筋对梁端弯矩的影响.在侧移达到±86mm后，角节点靠近梁侧现浇板板面钢筋应变略有下降，分析该现象，是由于加载后期角节点处直交梁扭转开裂降低了现浇板参与受拉的程度，而边节点则没有出现这种现象.

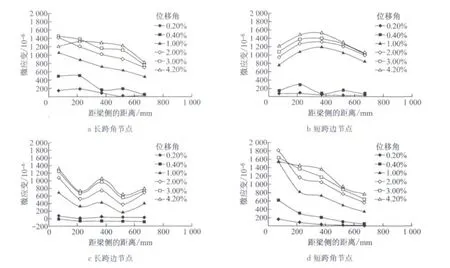
图8 一层现浇板受拉时钢筋应变（板面钢筋）Fig.8 The strain of slab longitudinal reinforcement in slab-in-tension case（top layer）

3.2 现浇板对梁端弯矩的影响

已有研究表明［5］，现浇板受拉时，由于板钢筋的参与作用将对梁端弯矩产生较大影响，故现浇板受拉状态下，按照实测数据计算的各个梁端部在2%层间侧移角时的弯矩与不考虑现浇板作用所计算的梁抗弯承载力对比如图9所示.

图9 梁端弯矩值Fig.9 The moment of beams

对比图9各个节点形式，在层间侧移角为2.0%时，考虑现浇板钢筋应力计算所得的梁端弯矩比不考虑现浇板作用计算的梁弯矩大45.3%～124.3%.由此可见，由于现浇板的作用使得梁端弯矩增大，若不充分考虑该影响是不安全的.

3.3 现浇板有效翼缘宽度

为便于考虑由于板纵筋参与受拉引起的梁端负弯矩的提高，采用有效翼缘宽度来计算板纵筋的作用.按照等效的原则，在某一级位移下，等效宽度范围内的板筋应变均等于主梁纵筋应变，且等效宽度范围内板筋和主梁纵筋承受拉力之和等于全板宽范围内板筋和主梁纵筋承受拉力之和［11］，如图10所示.计算公式如式（1）.

图10 现浇板有效翼缘宽度Fig.10 The effective slab width

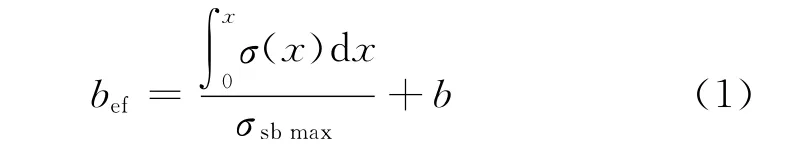
式中：bef为现浇板受拉有效翼缘宽度；b为主梁宽度；σsbmax为板纵向钢筋的最大应力，一般取梁侧位置处板纵向钢筋的应力；σ（x）为现浇板应力.

由公式 （1）及相关文献所提供的公式计算的现浇板在2%层间侧移角以及极限状态下的有效翼缘宽度如表4所示.由表4可知，利用Pantazopoulou公式计算的边节点有效翼缘宽度在侧移较大时计算值偏大；利用 Paulay&Park［11］，Zerbe［2］，Durrani［8］，Ehsani［9］和郑士举［7］公式计算的角节点的有效翼缘宽度偏低，与试验值差别较大；Zerbe、蒋永生［6］和郑士举计算的边节点有效翼缘宽度较为合适.综上可以看出，现有的有效翼缘宽度计算公式离散性大，精度不高，实际工程应用困难，故有效翼缘宽度的实际和计算模型取值还需要进行系统的研究.

表4 现浇板有效翼缘宽度取值Tab.4 The value of effective slab width of the cast in-situ slabs

3.4 拉压杆模型

从表4可以得出，现浇板钢筋参与工作程度与结构侧向变形大小有很大关系，按照式 （1）计算的极限状态下的有效翼缘宽度较2%层间侧移角下的略大，故本文偏于安全考虑，有效翼缘宽度计算模型取为在极限状态下.结合试验现象和分析，提出一种新的现浇板受力工作模型——拉压杆模型.该模型是将受压混凝土简化成压杆，受拉钢筋简化成拉杆.本文的拉压杆模型参考了文献［1，10，12-13］，形式如图11所示.在该模型中，假定直交梁和主梁的纵筋屈服，混凝土压力传入塑性铰位置A处；并假定板宽x的范围内板纵筋屈服，如图11所示，图中fy为主梁纵筋屈服强度；As为主梁纵筋面积；fy-tr为直交梁纵筋屈服强度；As-tr为直交梁纵筋面积；lp为塑性铰长度；sb为现浇板纵筋间距；fyb为现浇板钢筋屈服应力；Asb为现浇板钢筋面积.

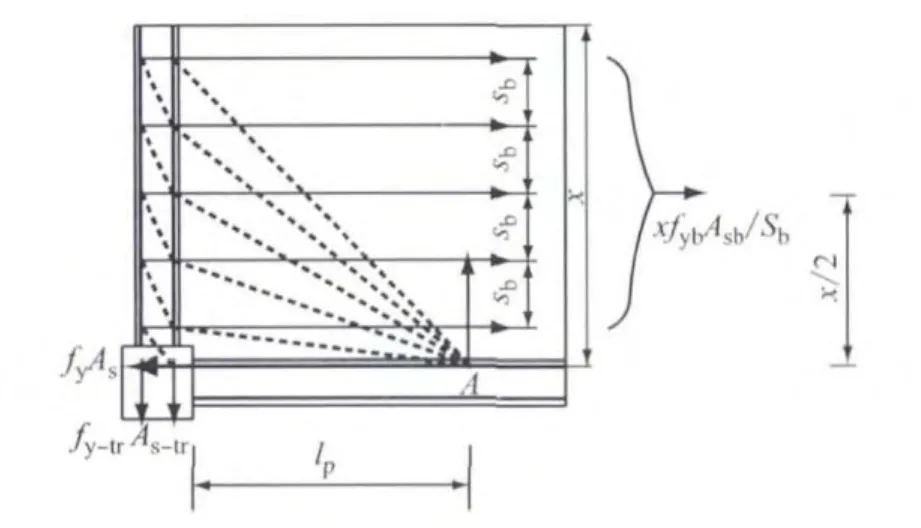
图11 有效翼缘宽度计算简图Fig.11 The calculation diagram of effective slab width

依据图11，钢筋拉力对A点取矩，得

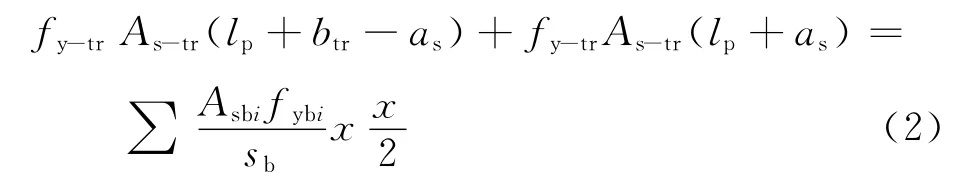
式中：btr为直交梁宽度；as为钢筋至构件边缘的距离；Asbi为第i层现浇板钢筋面积；fybi为第i层现浇板钢筋屈服应力.

对式（2）进行求解，得到x的取值为

式（3）未能考虑板的长宽比对x的影响.试验结果表明，纵向框架主梁的跨度不同，现浇板有效翼缘宽度不同，根据文献［2-5］中的数据，计入跨度影响后的调整式为

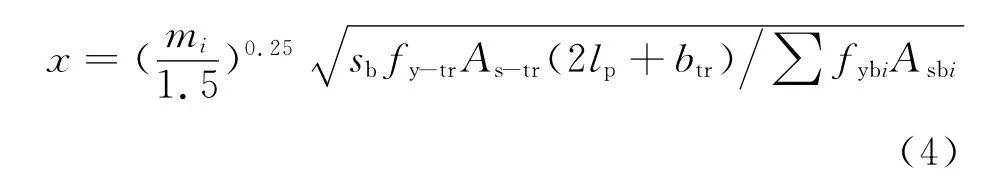
式中：mi为第i跨现浇板的长宽比.

则有效翼缘宽度表达式为

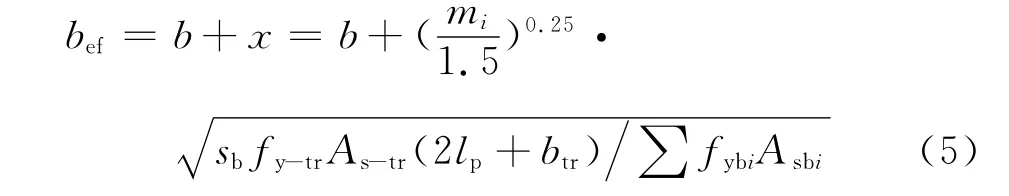
式（5）考虑的主要影响因素有：现浇板长宽比、直交梁宽度、直交梁纵筋面积和屈服强度、现浇板钢筋面积和间距等。将试验数据代入式（5），计算得出的板有效翼缘宽度与实际宽度对比如表5所示.从表5中可以看出，使用拉压杆模型计算所得到的结果与试验结果符合良好，平均误差为9.73%，表明使用拉压杆模型计算有效翼缘宽度是可行的.较以往的计算方法而言，式 （5）计算方便，考虑了多种因素的影响，可以应用于工程实际.

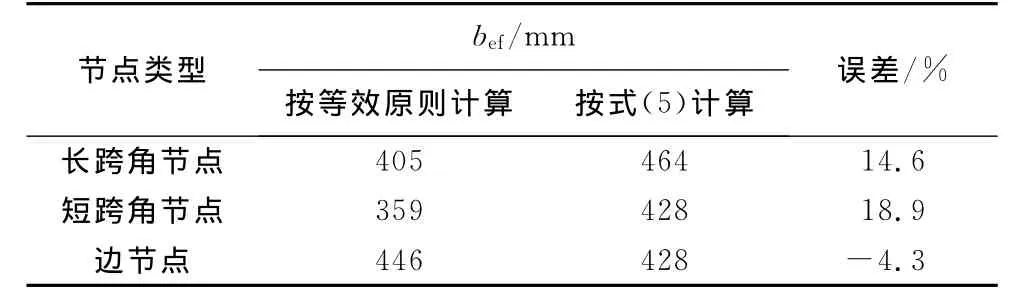
表5 有效翼缘宽度bef的计算结果比较Tab.5 The comparison between the calculated results of befand the test results

4 结论

本文完成了空间框架的低周反复试验，主要对现浇板对空间框架抗震性能的影响以及有效翼缘宽度理论进行了研究.主要结论如下：

（1）现浇板对框架的破坏机制有一定的影响，KJ-1为“强柱弱梁”破坏机制，而KJ-2转为“强梁弱柱”破坏机制；由于现浇板的存在，KJ-2直交梁发生扭转，扭转裂缝集中在约1倍梁高范围.

（2）现浇板的存在改善了模型的整体性能与承载力，KJ-2峰值荷载较KJ-1有明显提高；KJ-2的滞回曲线与KJ-1滞回曲线相似，但滞回环包络面积增大；现浇板的存在降低了结构的变形能力.

（3）现浇板纵筋应变随侧向位移的增大而增大，且角节点处较边节点处板筋应变大；现浇板的存在增大了梁端承受弯矩的能力，该现象对“强柱弱梁”的形成不利.

（4）本文提出的拉压杆模型可较好地反映现浇板参与受力的实际情况，计算方便，可以更有效应用于工程实际.

［1］ Franco M A，Mitchell D，Patrick P.Role of spandrel beam on response of slab-beam-column connections［J］.Journal of Structural Engineering，1995，121（3）：408.

［2］ Zerbe H E，Durrani A J.Seismic response of connections in two-bay reinforced concrete frame subassemblies with a floor slab［J］.ACI Structural Journal，1990，87（4）：406.

［3］ Qi X，Pantazopoulou S J.Response of RC frame under lateral loads［J］.Journal of Structural Engineering，1990，117（4）：1167.

［4］ Ammerman O V， French C W.R／C beam-column-slab subassenblages subjected to lateral loads ［J］.Journal of Structural Engineering，1989，115（6）：1289.

［5］ French C W，Boroojerdi A.Contribution of R／C floor slabs in resisting lateral loads［J］.Journal of Structural Engineering，1989，115（1）：1.

［6］ 蒋永生，陈忠范，周绪平，等.整浇梁板的框架节点抗震研究［J］.建筑结构学报，1994，15（6）：11.JIANG Yongsheng，CHEN Zhongfan，ZHOU Xuping，et al.Aseismic research on RC frame joint of monolithically casted slab［J］.Journal of Building Structures，1994，15（6）：11.

［7］ 郑士举，蒋利学，张伟平，等.现浇混凝土框架梁端截面有效翼缘宽度的试验研究与分析［J］.结构工程师，2009，25（2）：134.ZHENG Shiju，JIANG Lixue，ZHANG Weiping，et al.Experimental research and analysis of effective flange width of beam end section in cast-in-situ concrete frames［J］.Structural Engineers，2009，25（2）：134.

［8］ Durrani A J，Wight J K.Earthquake resistance of reinforced concrete interior connections including a floor slab［J］.ACI Structure Journal，1987，84（5）：400.

［9］ Ehsani M R，Wight J K.Effect of transverse beams and slab on behavior of reinforced concrete beam-to-column connections［J］.ACI Journal Proceedings，1985，82（2）：188.

［10］ Pantazopoulou S J，Moehle J P.Truss model for 3-D behavior of R C exterior connections［J］.Journal of Structural Engineering，1990，116（2）：298.

［11］ Paulay T，Park R.Joints in reinforced concrete frames designed for earthquake resistance ［R］.Christchurch：University of Canterbury Christchurch，1984.

［12］ Pantazopoulou S J， Moehle J P，Shahrooz B M.Simple analytical model for T-beams in flexure［J］.Journal of Structural Engineering，1988，114（7）：1507.

［13］ Mezzina M，Palmisano F，Raffaele D.Design simply supported R C bridge decks subjected to in-plane actions：strut-and-tie model approach［J］.Journal of Earthquake Engineering，2012，16（4）：496.