超深基坑工程渗流耦合理论研究进展

王春波，丁文其，陈志国，朱 令

（1.同济大学 土木工程学院，上海200092；2.同济大学 岩土及地下工程教育部重点实验室，上海200092；3.江苏铭城建筑设计院有限公司，江苏 盐城224000）

基坑工程实际上是由围护结构、地基土、地下水及地下结构工程桩等组成的一个复杂系统，通常认为开挖深度H≥6m或者有支护结构的基坑为深基坑，而开挖深度H≥15m的基坑则为超深基坑［1］.随着我国基础设施建设的快速发展，我国的基坑工程发展迅速，其主要标志是基坑开挖规模越来越大、开挖深度越来越深，如上海基坑最大开挖深度已达41m.超深基坑工程涉及到的渗流主要是指上部潜水疏干降水，承压水减压降水和围护结构渗漏产生的渗流等，基坑工程的渗流不仅会引起土体结构、土体强度发生变化，还会对围护结构上的水土压力、基坑坑底隆起量、基坑周边地表及建筑物的沉降变形产生影响，严重的还会造成突涌、流砂等工程事故.在超深基坑工程设计及施工中不仅要对上部潜水降水引起的坑底隆起量、围护结构侧向变形以及周边建筑物的沉降变形进行分析，还要对承压水降水引起的地表沉降以及对周边建筑物的影响进行渗流耦合分析，但承压水的降水要坚持按需降水的原则.由此可见，开展超深基坑工程流固耦合方面的研究无论是理论研究方面还是指导工程实践方面都具有重要的意义.

本文分别从渗流耦合模型、渗流理论、渗流耦合中渗透系数的动态变化以及基坑工程降水对土体强度的影响四方面总结基坑工程渗流耦合理论研究现状，并进行相应的分析和讨论，针对超深基坑工程的复杂性和特殊性，对超深基坑工程的水土耦合研究方向阐述一点认识，以期为此方面的研究提供参考.

1 渗流场、应力场耦合模型研究

岩土工程中存在着多种作用，如水力学、力学、热学等作用，在很多情况下这些作用同时存在而且相互影响，渗流场与应力场之间的相互作用称为渗流耦合作用，其渗流耦合示意图如图1所示.

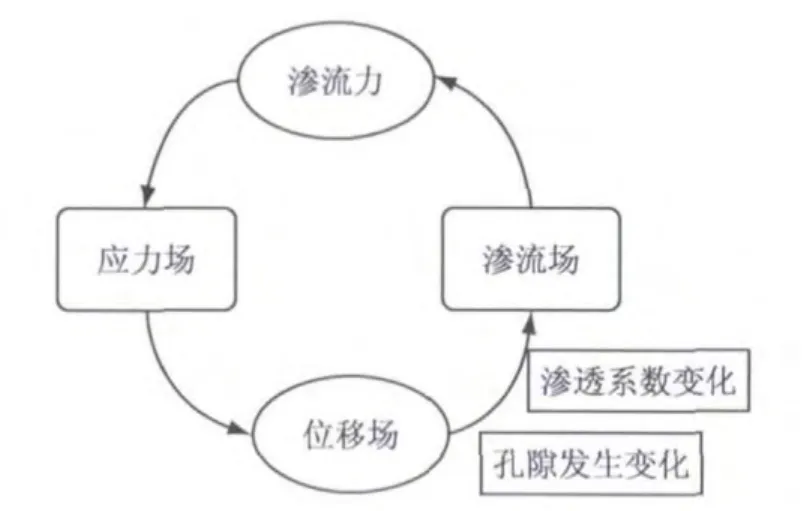
图1 渗流场、应力场耦合机理示意图Fig.1 Schematic diagram of coupling mechanism between seepage field and stress field

Terzaghi［2］首先研究了饱和多孔介质中流体的流动，并建立了一维固结模型，然而，Terzaghi一维固结理论的流固耦合机理在力学上并不严格；于是Biot［3］进一步研究了三向变形材料与孔隙压力的相互作用，利用线弹性本构关系和Darcy定律，建立了比较完善的三维固结理论；Zienkiewicz和Shiomi［4］在Biot三维固结理论的基础上提出了广义的Biot公式，该公式可同时考虑几何和材料的非线性特性，但事实上岩土体材料各向异性明显，基于此，Savage和Bradock［5］将Biot三维固结理论应用到横观各向同性孔隙介质中.

在经典渗流耦合理论的基础上，我国岩土工作者基于具体的工程实际，对传统的渗流耦合模型进行了修正，并且取得了较大的成果.陈小平等［6］对软土蠕变-固结特性、计算模型、模型的数值求解方法和工程应用等进行了系统的研究，建立了实用的非线性粘弹性固结模型；周志芳等［7］基于不同水文地质层水流运动特征差异，提出了双层结构数学模型；骆祖江等［8］以Biot三维固结理论为基础引入邓肯-张非线性弹性模型和渗透率动态模型，建立了浅层地下水开采与地面沉降的三维全耦合模型；廖红建等［9］基于饱和-非饱和土体渗流理论将土体渗透系数与基质吸力分别引入到基坑降水的应力应变分析中，采用土体弹塑性本构模型，对深基坑开挖中饱和-非饱和土体渗流进行了分析研究.杨林德等［10］将饱和土体视为均质连续的各向异性弹塑性多孔介质，根据虚位移原理推导出饱和土体各向异性渗流直接耦合的有限元计算公式.陈波等［11］在推导多孔介质三场耦合数学模型控制方程上系统地推导了6节点三角形单元的固液两相介质的温度场、变形场、渗流场三场耦合问题的分析方法.

综上研究的耦合模型中有线弹性模型、非线性弹性模型、黏弹性模型、弹塑性模型等，然而基坑工程尤其是超深基坑工程，土体开挖卸荷量大，应力路径复杂，基坑土体实际上是处于一个应力水平不断变化的环境中，渗流耦合模型不仅要体现基坑工程应力路径的复杂性，土体的非线性特性，还要能反映渗流场对应力场的影响变化，所以通过修改原有模型得到与工程实际更加接近的渗流耦合模型是实现真耦合的基础.

2 渗流理论研究

自Darcy建立了Darcy线性渗流定律以来，渗流理论及其应用研究得到了迅速的发展，其表达式如式（1）所示.裘布衣以Darcy定律为基础，研究了单向和平面径向地下水流的稳定运动，Forchheimer等又研究了更为复杂的地下水渗流，从而奠定了地下水稳定渗流理论的基础［12～15］.

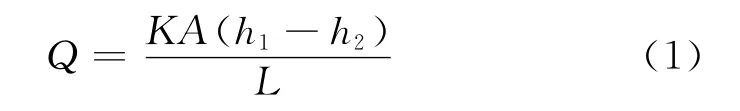
式中：Q为渗流量；K为砂样渗透系数，也称水力传导系数；A为试验土样截面积；h1，h2分别为通过砂样前后的水头；L为砂样沿水流方向的长度.

然而，工程实际中真正的稳定流很少，大多数为非稳定流，于是Boussinesq提出了地下水非稳定流的偏微分方程；Meinzer研究了地下水运动的不稳定性以及承压含水层的贮水性质，Theis在此基础上又提出了地下水向承压水井渗流的非稳定流公式，并将热传导方程式的求解技术应用到研究地下水运动规律领域，开创了现代地下水运动的新纪元［16］.

Jacob参照热传导理论建立了地下水渗流运动的基本微分方程.

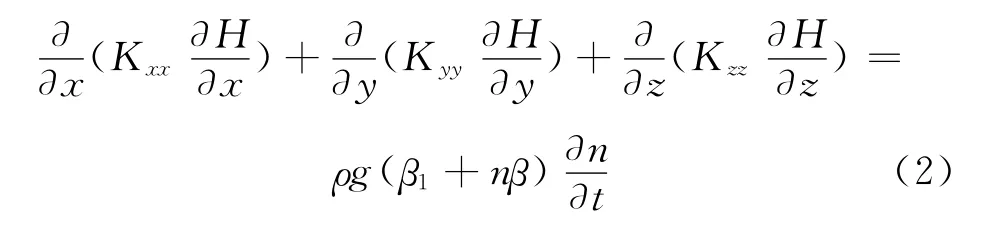
式中：Kii为i（i=x，y，z）方向的渗透系数；H为水头；ρ为水的密度；g为重力加速度；β1为岩土骨架的弹性压缩系数；β为地下水的弹性压缩系数；n为介质的孔隙率.

Hantush等进行了不同条件下地下水非稳定渗流运动的理论研究，并各自推导出各种条件下地下水非稳定渗流运动的解析公式，Richards［18］将Darcy的线性渗流理论推广应用到非饱和渗流中后，人们开始了非饱和渗流的研究.Neuman［17］最早应用有限元法求解饱和与非饱和渗流问题；Fredlund等［19～24］假定气相是连续的，应用Fick定律和Darcy定律提出了求解非饱和土固结过程的孔隙气压力，用Galerkin加权余量原理推导了二维稳定渗流的有限元形式；Freeze等［25］认为对大多数实际问题来讲，考虑液相流动的非饱和渗流的单相近似技术的计算结果与考虑气、液两相流动的非饱和渗流的计算结果之间的误差可以忽略；Forsyth［26］通过计算地下水非饱和单相流动与两相流动模型，得出采用两相流的分析方法与单相流的分析方法其计算结果是有差别的.

我国学者在饱和-非饱和渗流理论方面也进行了大量的研究，并且取得了许多重要的成果.汪自力等［27］利用数值积分时高斯点处压力选取计算参数来进行刚度矩阵计算，解决了单元内部存在的非饱和渗透系数不同的问题.吴梦喜等［28］以有限差分方式表示饱和度对孔隙水压力的偏导数，从而消除了数值弥散现象.朱京义等［29］用Galerkin法建立了非饱和土水两相不相容、不可压缩渗流的有限元方程.王飞等［30］基于一阶Taylor有限元法，实现了三维稳定渗流场随机有限元分析.刘洋等［31］在分析渗流连续介质力学模型的基础上，采用描述多孔介质中固相颗粒和液相流体耦合的细观力学模型，通过求解平均Navier-Stoke方程，对二维渗流问题进行了模拟验证.

目前对渗流的研究大多以Darcy定律为基础，实际上Darcy定律有一定适用范围.图2中J为水力梯度，q为渗流速度，根据Reynolds数判断［32］，Re不超过10时，地下水运动才符合Darcy定律，也可以从多孔介质中的水流状态判断Darcy定律的适用范围，当渗流流速由低到高时，可把多孔介质中的地下水运动状态分为3种情况，如图3所示.

图2 渗流速度与水力梯度的实验关系（据Bear J）Fig.2 The experimental relationship of the seepage velocity and hydraulic gradient（By Bear J）

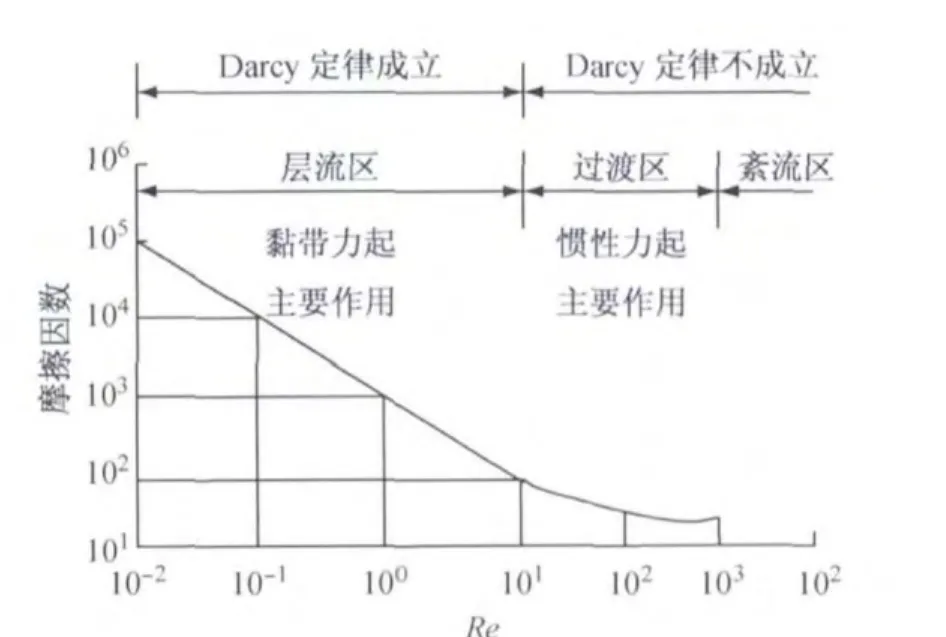
图3 多孔介质中流动分类示意图（据Bear J）Fig.3 Classification schematic of flow in porous media（By Bear J）

（1）当地下水低速度运动时，即Re为0.01～10之间的某个值时，为黏滞力占优势的层流运动.

（2）随着流速的增大，即当Re为10～100之间时，为由黏滞力占优势的层流运动转变为惯性力占优势的层流运动再转化为紊流运动的过渡带.

（3）高Re时为紊流运动，显然，Darcy定律适用范围为地下水低流速，以黏滞力占优势的层流运动范围，对于超深基坑工程，基坑开挖深度深，地下水流速大，其渗流有可能偏离Dracy定律，尤其是降水井井壁附近处的渗流更不满足Dracy定律，如仍按Dracy定律进行渗流耦合分析工作，会使设计计算结果偏小，从而增大发生工程事故的风险.但就目前来说还没有公认的适用于Re＞1～10情况下的非线性运动方程，常用的一种形式［33］如式（3）所示.

式中：J为水力梯度；a，b为试验参数；1.6≤m≤2.0，当a=0，m=2.0时，v=kJ1/2即为 Cheny公式.

由于受到环境的限制或者止水的要求，超深基坑工程的渗流与其他工程的渗流既有区别又有共性，如图4所示为不同类型基坑工程［32］（第1类基坑，基坑围护结构深入隔水层（即含水层底板）中，井点降水以疏干基坑内的地下水为目的；第2类基坑，基坑围护结构深入隔水层（即含水层顶板）中，井点降水以降低基坑下部承压含水层的水头，防止基坑底板隆起或突水产生流砂为目的；第3类基坑，基坑围护结构深入承压含水层中，井点降水的前期以降低基坑下部承压含水层水头为目的，后期以疏干承压含水层为目的），不同插入深度的围护结构其渗流场的分布不同.由图4可知，支挡结构的存在使得基坑工程支护结构附近处的渗流主要以竖向渗流为主，远离支护结构处和承压含水层内的渗流则主要为水平向渗流.

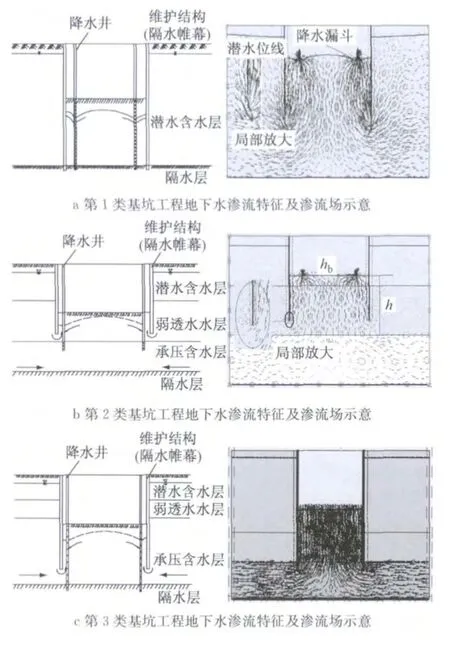
图4 不同类基坑工程降水渗流矢量图Fig.4 Seepage vector diagram of different types of foundation pits

在超深基坑较高水力梯度作用下，渗流偏离了层流条件，随着雷诺数的增加，流体的流动明显偏离了Darcy定律适用条件，流速和水力梯度不再成直线关系.因此，探讨有围护结构的超深基坑工程渗流规律或者对Darcy定律进行修正，是开展深基坑水土耦合理论研究的关键.

3 土体渗透性研究

由Darcy渗流定律可知，土体渗透系数k可用渗透率k0来表示，即

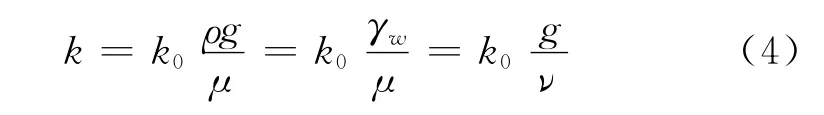
式中：k0为渗透率；μ为水的绝对粘度；ν为运动黏滞系数.

由式（4）可知，土体的渗透系数不仅与渗透率有关（渗透率的大小与土体孔隙度、饱和度等因素有关），还与流体的物理性质有关（流体黏滞度、黏滞系数）.饱和土体孔隙中充满水，渗透系数k只是孔隙率n的函数，若把k视为常量，则属于线性固结问题；k视为变量则属于非线性固结问题.大量实验研究表明，土体等多孔介质处于饱和状态时，渗透率k0或渗透系数k可以表示为孔隙率n或孔隙比e的函数，其具体关系式可归纳为如下几种情况：

（1）砂性土的渗透率［34］

式中：n0，n分别为土体初始孔隙率和变化后孔隙率；k′，k分别为与n0，n相对应的渗透系数.

式（14）和式（12）体现了应变场（应力场）对渗流场的影响，在渗流耦合中若将渗透系数设定为常数，则属于假耦合分析或称为“半耦合分析”，因为此时的渗流耦合分析只能反应渗流场对应力场的影响，却不能体现应力场对渗流场的影响.

对于非饱和土，Richards将饱和土Darcy定律延伸至非饱和土，但非饱和土渗透系数kw是孔隙率n和饱和度S的函数即体积含水量θ的函数，由于体积含水量、饱和度与基质吸力之间的关系可用土-水特征曲线来体现，所以渗透系数也是基质吸力的函数.土-水特征曲线及渗透性函数通常都由试验测定，计算中可以根据实测的土-水特征曲线和渗透性函数确定介质的渗透系数.

Gardner认为渗透系数kw与体积含水率θw之间满足幂函数关系

式中：a，b为试验常数.

随后 Campbell［37］对式（15）进行了修正

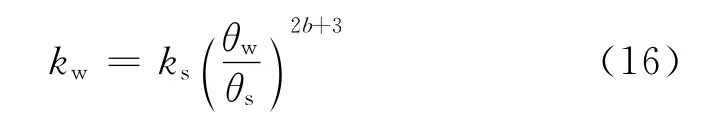
式中：ks为饱和渗透系数；θs为饱和体积含水率.

Malcolm［38］则认为渗透系数与体积含水率满足指数型函数关系，即

Averjanor［39］在考虑土体中气相值的基础上，提出渗透系数与土体饱和度之间的关系为幂函数关系，即

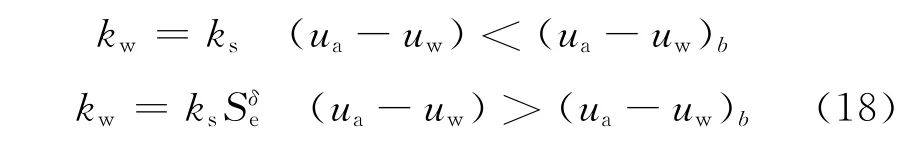
式中：（ua-uw）为基质吸力；（ua-uw）b为进气值；ua为孔隙气压力；uw为孔隙水压力；Se为土体有效饱和度；δ为经验常数，在δ的选取上，许多学者提出了不同的观点，Averjanov建议采用3.5，Yuster建议采用2，Brook和Corey认为δ应该按下式计算：δ=，λ为孔隙尺寸分布指标，

Brook-Corey提出渗透系数与基质吸力之间的关系为幂函数关系，其表达式如下：

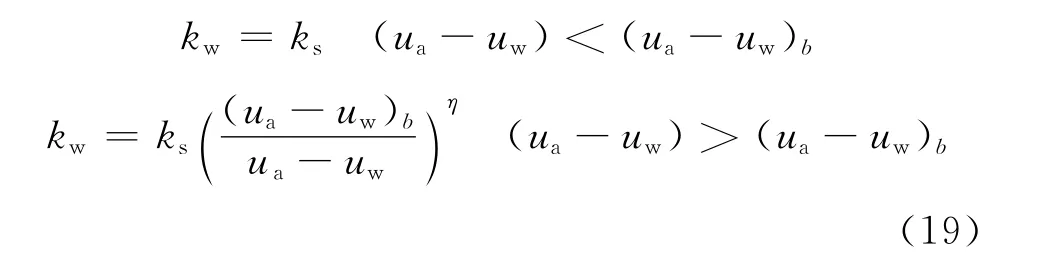
式中：η为与孔隙尺寸有关的参数.

综上研究可以发现，土体渗透系数是应力场、渗流场相互耦合的“桥梁”，若将其视为常数，则不能体现应力场对渗流场的影响，也就不能实现两场的相互耦合分析，而且无论是饱和土还是非饱和土，土体水平向和竖向渗透系数相差明显.因此，第一，只有明确土体水平向和竖向渗透系数与孔隙率、体积含水量之间的关系，才能使计算结果与实际更加接近.第二，超深基坑工程由于降水深度的增加，渗流路径所经历的土层变化较大，在经历饱和土、非饱和土甚至隔水层相互混合的土层时，土体渗透性变化不一，这就需要探求混合土层渗透系数的变化模式；第三，工程中隔水层和透水层没有明确的界限，完全的不透水层也是不存在的，超深基坑中在较高的水力梯度作用下隔水层会转化为透水层，使得土层渗透性发生根本变化.因此探讨非饱和-饱和-隔水层混合土层的渗透系数表达式是研究超深基坑渗流耦合的重要环节.

4 工程降水对土体强度的影响

对超深基坑工程来说，影响土体强度的因素很多，其中最重要的是排水条件和应力历史.超深基坑工程排水固结后土体有效应力增加，土体黏聚力、内摩擦角发生变化，试验研究表明，降水后土体黏聚力有较大程度的提高而内摩擦角变化不大.不同土体强度增长方式以及变化大小不同，目前，有关基坑降水对土体抗剪强度的影响国内外研究较少，吴林高［32］通过大量的试验得出降水前后土体的摩擦角几乎不变，而黏聚力由于前期固结压力的增大而提高，降水后的土体，在以后的受荷条件下，有效应力的增长总是在整个应力增长过程中占据主要地位，这与降水前的土体应力增长情况明显不同，降水后在相同应力水平下，土体呈现较小的变形量.

李琳［40］以上海第三层灰色黏土和第四层灰色淤泥质黏土为试验对象，研究了不同应力水平时不同降水深度对土体强度增长的影响，如表1所示.但没有给出降水对土体强度参数影响的定量关系式，因而对计算分析作用不大.

表1 上海淤泥质黏土降水后抗剪强度的相对增长Tab.1 Relative increase in shear strength of Shanghai silty clay after dewatering

对于超深基坑工程，在大开挖、高水头作用下，土体实际上是受到较大的加卸荷反复作用，土体的强度必然会受到影响，探讨降水对土体强度影响的方法主要有两种，一是通过现场降水试验，直接选取降水后的土样测其强度，从而建立水位降深与土体强度之间的定量关系式；二是从土力学机理出发进行理论分析，然后通过室内试验进行验证分析.由此可建立降水、开挖作用下土体强度参数的变化规律，尤其是对于不同的土体建立降水深度与土体强度参数变化的定量关系，对于分析基坑工程坑底隆起、被动区土压力以及渗流耦和作用都具有重要的意义，也能够更准确地反映渗流场对应力场的影响.

5 结语

基坑工程中地下水的渗流由于受多种因素的影响，渗流研究较为复杂，相比之下，超深基坑工程具有开挖深度深、开挖规模大、坑内外水力梯度大、基坑围护结构复杂等特点，这就使得渗流耦合问题的研究更加困难，通过上述总结分析，对于超深基坑工程的渗流耦合问题，可以从以下几方面进行研究：

（1）渗流耦合模型方面：超深基坑工程降水引起的渗流持续时间长，土体参数变化显著，在渗流耦合分析中，选取的土体本构模型应该既能体现超深基坑工程复杂的应力路径、土体非线性特性，又能反映渗流场对应力场的影响变化，是超深基坑工程渗流耦合分析的基础.

（2）渗流理论方面：Darcy定律实质上是低阶的Navier-Stoke方程，仅当孔隙流是薄层流、惯性力可以忽略的情况下才有效，超深基坑水力梯度较大，在较大的水力梯度作用下，将会产生非薄层流，较大的孔隙流体速率，渗流会偏离Darcy定律，如何对Darcy定律进行修正是进行渗流耦合分析的关键.

（3）土体渗透性方面：随着基坑开挖深度的增加，基坑降水引起的渗流路径加长，流经性质各异的多重土层，包括饱和土、非饱和土及不透水层等，在渗流耦合分析时，土体渗透系数的变化模式可能不符合某一单一的变化模式，如幂函数型、指数型，探求与实际工程地质、水文地质更加接近的土体各向异性渗透系数与土体变形的关系式是实现应力场、渗流场相互耦合的关键.

（4）土体强度方面：大的降水量，对超深基坑工程土体将产生二次固结作用，在二次固结压力作用下，土体参数将发生变化.相关试验结果表明，降水前后土体内摩擦角几乎不变，黏聚力由于前期固结压力的增加而提高，降水后土体强度显著提高.建立降水量与土体强度参数之间的定量关系式是超深基坑渗流耦合分析的又一个重要研究方向.

［1］ 林鸣，徐伟，杨玉泉，等.深基坑工程信息化施工技术［M］.北京：中国建筑工业出版社，2006.LIN Ming，XU Wei，YANG Yuquan，et al.Information construction technology of deep foundation engineering［M］.Beijing：China Architecture &Building Press，2006.

［2］ Terzaghi K.Theoretical soil mechanics［M］.New York：Wiley and Sons Inc，1943.

［3］ Boit M A.General theory of three dimensional consolidation［J］.Journal of Applied Physics，1941（12）：155.

［4］ Zierkiewicz O C，Shiomi T.Dynamic behaviour of saturated porous media：the generalized Biot formulation and its numerical solution［J］.International Journal for Numerical and Analytical in Geomechanics，1984（8）：71.

［5］ Savage W Z， Bradock W A.A model for hydrostatic consolidation of Pierre shale［J］.International Journal for Rock Mechanics and Mining Sciences，1991，28（5）：345.

［6］ 陈小平，白世伟.软土蠕变-固结特性及计算模型研究［J］.岩石力学与工程学报，2003，22（5）：728.CHEN Xiaoping，BAI Shiwei.Research on creep-consolidation characteristic and calculation model of soft soil［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（5）：728.

［7］ 周志芳，朱宏高，陈静，等.深基坑降水与沉降的非线性耦合计算［J］.岩土力学，2004，25（12）：1984.ZHOU Zhifang，ZHU Honggao，CHEN Jing，et al.Nonlinear coupling calculation between dewatering and settlement of deep foundation pits［J］.Rock and Soil Mechanics，2004，25（12）：1984.

［8］ 骆祖江，曾峰，李颖.地下水开采与地面沉降控制三维全耦合模型研究［J］.吉林大学学报：地球科学版，2009，39（6）：1080.LUO Zujing，ZENG Feng，LI Ying.Study on three-dimension full coupling model of groundwater exploitation and landsubsidence control［J］.Journal of Jilin University：Earth Science Edition，2009，39（6）：1080.

［9］ 廖红建，姬建.深基坑开挖中饱和-非饱和土体渗流-沉降耦合分析［J］.应用力学学报，2008，25（4）：637.LIAO Hongjian，JI Jian.Coupled analysis of seepage-settlement for saturated-unsaturated soil in deep foundation pit excavation［J］.Chinese Journal of Applied Mechanics，2008，25（4）：637.

［10］ 杨林德，杨志锡.各向异性饱和土体的渗流耦合分析和数值模拟［J］.岩石力学与工程学报，2002，21（10）：1447.YANG Linde，YANG Zhixi.Coupling analyses and numerical simulation on seepage flow in anisotropic saturated soils［J］.Chinese Journal of Rock Mechanics and Engineering，2002，21（10）：1447.

［11］ 陈波，李宁，禚瑞花.多孔介质的变形场-渗流场-温度场耦合有限元分析［J］.岩石力学与工程学报，2001，20（4）：467.CHEN Bo，LI Ning，ZHUO Ruihua.FEM analysis on fully coupled thermo-hydro-mechanic behavior of porous media［J］.Chinese Journal Rock Mechanics and Engineering，2001，20（4）：467.

［12］ 郭东屏，宋焱勋，钱会，等.地下水动力学［M］.西安：陕西科学技术出版社，1994.GUO Dongping，SONG Yanxun，QIN Hui，et al.Groundwater dynamics［M］.Xi’an：Shaanxi Science and Technology Press，1994.

［13］ 贝尔J.多孔介质流体力学［M］.北京：中国建筑工业出版社，1996.Bear J.Fluid mechanics in porous media［M］.Beijing：China Architecture and Building Press，1996.

［14］ 顾慰慈.流体计算原理及应用［M］.北京：中国建筑工业出版社，2000.GU Weici.Principle and application of computational fluid［M］.Beijing：China Architecture and Building Press，2000.

［15］ 吴子牛.计算流体力学基本原理［M］.北京：科学出版社，2001.WU Ziniu.The basic principles of computational fluid dynamics［M］.Beijing：Science Press，2001.

［16］ 孔祥言.高等渗流力学［M］.合肥：中国科技大学出版社，1999.KONG Xiangyan.Advanced fluid mechanics［M］.Hefei：Press of University of Science and Technology of China，1999.

［17］ Neuman P S.Saturated-unsaturated seepage by finite elements［J］.Journal of the Hydraulics Division，ASCE，1973，99（12）：2233.

［18］ Richards L A.Capillary conduction of liquids through porous medium［J］.Physics，1931，1（5）：318.

［19］ Fredlund D G， Xing A E.Equation for the soil-water characteristic curve［J］.Canadian Geotechnical Journal，1994，31（4）：521.

［20］ Fredlund D G，Xing A，Huang S.Predicting the permeability function for unsaturated soils using the soil-water characteristic curve［J］.Canadian Geotechnical Journal，1994，31（4）：533.

［21］ Fredlund D G，Xing A，Fredlund M O，et al.The relationship of the unsaturated soil shear strength to the soil-water characteristic curve［J］.Canadian Geotechnical Journal，1996，33（3）：440.

［22］ Fredlund D G，Hansan J U.One-dimensional consolidation theory：unsaturated soils［J］.Canadian Geotechnical Journal，1979，16（3）：521.

［23］ Fredlund D G，Rahard H.Soil mechanics for unsaturated soils［M］.New York：John Wiley and Sons Inc，1993.

［24］ Fredlund D G，Morgenstem N R，Widger R A.The shear strength of unsaturated soils［J］.Canadian Geotechnical Journal，1978，15（3）：313.

［25］ Freeze R A，Cherry J A.Groundvoator：Englewood cliffs［J］.Mternectionell fornal of Rock Meehanics and mining Sciences，1980，17（6）：A111.

［26］ Forsth P A.Comparison of the single-phase and two-phase numerical model formulation for saturated-unsaturated groundwater flow ［J］.Computer Methods in Applied Mechanics and Engineering，1988，69（7）：243.

［27］ 汪自力，张俊霞，李莉.饱和-非饱和渗流模型在多层自由面渗流分析中的应用［J］.人民黄河，1997（1）：34.WANG Zili，ZHANG Junxia，LI Li.Application of saturatedunsaturated flow model in analysis of multi-layer free surface flow［J］.Yellow River，1997，（1）：34.

［28］ 吴梦喜，高莲士.饱和-非饱和土体非稳定渗流数值分析 ［J］.水力学报，1999，（12）：38.WU Mengxi，GAO Lianshi.Saturated-unsaturated unsteady seepage numerical analysis ［J］.Journal of Hydraulic Engineering，1999（12）：38.

［29］ 朱京义，张彦.非饱和土水气两相不相容，不可压缩渗流有限元分析［J］.武汉大学学报：工学版，2002，35（4）：44.ZHU Jingyi，ZHANG Yan.Finite element modeling of twophase immiscible and incompressible seepage in unsaturated soil［J］.Engineering Journal of Wuhan University，2002，35（4）：44.

［30］ 王飞，王媛，倪小东.渗流场随机性的随机有限元分析［J］.岩土力学，2009，30（11）：3539.WANG Fei，WANG Yuan，NI Xiaodong.Analysis of random characteristics of seepage field by stochastic finite element method［J］.Rock and Soil Mechanics，2009，30（11）：3539.

［31］ 刘洋，李飞，柴晓庆，等.渗流的PFC-CFD耦合细观数值模拟［J］.水文地质工程地质，2008（2）：66.LIU Yang，LI Fei，CHAI Xiaoqing，et al.A PFC-CFD coupled model in meso-scale for seepage［J］.Hydrogeology and Engineering Geology，2008（2）：66.

［32］ 吴林高.工程降水设计施工与基坑渗流理论［M］.北京：人民交通出版社，2003.WU Lingao.Design and execution of dewatering &theory of seepage in deep excavation ［M ］.Beijing： China Communications Press，2003.

［33］ 薛禹群，谢春红.地下水数值模拟 ［M］.北京：科学出版社，2007.XUE Yuqun，XIE Chunhong.Numerical simulation for groundwater［M］.Beijing：Science Press，2007.

［34］ Noorishad J.A finite element method for coupled stress and flow analysis in fractured rock mass［J］.International Journal of Rock Mechanics and Mining Sciences，1982，19（4）：185.

［35］ 吴梦喜.土体非饱和渗流与变形耦合分析方法及在心墙坝中的应用［D］.北京：清华大学土木水利学院，2000.WU Mengxi.Unsaturated soil seepage and deformation coupled analysis method and application in dam of the core wall［D］.Beijing：College of Cvil Engineering of Tsinghua University，2000.

［36］ 罗元华，孙雄.不同应力状态下地层渗透系数的变化及其对流体运移影响的数值模拟研究［J］.地球学报：中国地质科学学院院报，1998，19（2）：144.LUO Yuanhua，SUN Xiong.The numerical simulation of changes in permeability under different stress state and fluid movement［J］.Journal of China Gelogical Science，1998，19（2）：144.

［37］ Campbell G S.A simple method for determining unsaturated conductivity from moisture retention data［J］.Soil Science，1974，117（6）：311.

［38］ Malcolm R D.Numerical calculation of saturated-unsaturated infiltration in a cracked soil［J］.Water Resources Research，1985，21（5）：709.

［39］ Averjanov S F.About permeability of subsurface soils in case of incomplete saturated porous media［J］.Water Resources Research，1987，23（4）：542.

［40］ 李琳.工程降水对深基坑形状及周围环境影响的研究［D］.上海：同济大学土木工程学院，2007.LI Lin.Research on influence of dewatering on deep foundation shape and environment［D］.Shanghai：College of Civil Engineering of Tongji University，2007.