Generalized Rayleigh Wave Dispersion Analysis in a Pre-stressed Elastic Stratified Half-space with Imperfectly Bonded Interfaces

M.NeginS.D.Akbarov and M.E.Erguven

1　Introduction

The theory of elastic surface waves in layered half-spaces,though it is an old topic in classical sense,it has found highly important scientific and engineering applications through the last couple of decades.Fields of applications are vast but some notable areas might be acoustic,smart materials,metrology,Earth sciences,subsurface explorations,non-destructive testing and damage detection.Indeed,variety of mechanical,material and structural properties,presence of damages and/or cracks,different external loading,etc.make the study of these wave processes still an active and interesting field of research these days.

There are two types the most important investigations in this regard the first of which relates to study of the effect of imperfect bonding between the covering layer and half-space on a surface wave propagation and its characteristics.But the other one is the study of influence of initial stresses which exist in the constituents of the stratified half-space on this wave.

The investigations of the first type problems are motivated by very high sensitivity of the wave propagation characteristics to interface defects such as weak-bonding between the constituents which can be caused by interface damages or chemical actions and etc.The results of these investigations can be successfully applied for determination of various defects between the covering layer and half-space.

But the investigations of the second type problems are motivated by the non-destructive determination of mostly the residual(or initial)stresses in the elements of constructions.Currently the results of these investigations are successfully employed for determination of the mentioned residual stresses.At the same time,the foregoing investigations are also propounded the fundamental questions of the dynamics of the non-homogeneous deformable solid bodies.

It is evident from the foregoing discussions that the investigations of the generalized Rayleigh wave dispersion in a pre-stressed elastic stratified half-plane with imperfectly bonded interfaces,which is the topic of the present paper,lies at the junction of the above-noted two type problems.

Note that propagation of the elastic waves in pre-stressed bodies is studied by utilizing of the Three-dimensional Linearized Theory of Elastic Waves in Initially Stressed Bodies(TLTEWISB).The relations and equations of the TLTEWISB are obtained from the exact relations and equations of the non-linear theory of elastodynamics by linearization with respect to small dynamical perturbations.The general questions of the TLTEWISB have been elaborated in many investigations such as in works by Biot(1965),Truestell(1961),Eringen and Suhubi(1975),Guz(2004)and others.It should be noted that there are some versions of the TLTEWISB which were detailed in the monograph by Guz(2004).These versions of the TLTEWISB are distinguished from each other with respect to the magnitude of the initial strains.The version of the TLTEWISB developed for high-elastic materials,according to which the initial strains in the bodies are determined within the scope of the non-linear theory of elasticity without any restrictions on the magnitude of the initial strains,is called the large(or finite)initial deformation version.The version of the TLTEWISB,according to which,an initial stress-strain state in bodies is determined within the scope of the geometrical nonlinear theory of elasticity and changes to the elementary areas and volumes as a result of the initial deformation are not taken into account,is called the first version of the small initial deformation theory of the TLTEWISB.The second version of the small initial deformation theory of the TLTEWISB is the version,according to which,an initial stress-strain state in bodies is determined within the scope of the classical linear theory of elasticity.

The review of the investigations carried out before the year 2007 on the wave propagation in pre-stressed bodies has been made in the papers by Guz(2002),Guz(2005)and Akbarov(2007).The detail consideration of the results of these investigations was made in the monographs by Biot(1965),Eringen and Suhubi(1975),Guz(2004).The review of the more resent related investigations can be found in papers by Akbarov(2012),Akbarov and Ipek(2012),Akbarov;Agasiyev and Zamanov(2011)and etc.However,in considerable part of these works the interface between layers was assumed to be bonded perfectly,which it is not the real case in many applications.

Two classical boundary conditions,that are,perfect bonded interfaces and full slipping ones idealize real physical contact between two layers.In perfect contact condition also known as welded interfaces all the stress and displacement components are continuous across the interface,whereas,in the case of full slipping conditions also known as non-welded interfaces there is a discontinuity in the shear component of the displacement[Rokhlin and Wang(1991)].An actual interface conditions between two layers is much more complicated in mathematical modeling viewpoint and different investigators spent significant efforts to describe the real physical conditions by different mechanical models.To summarize some,Martin(1992)has reviewed imperfect interface models and formulated the problem mathematically.Pecorari(2001)has investigated the scattering problem of a Rayleigh wave by surface-breaking cracks with partial contact interfaces.Leungvichcharoen and Wijeyewickrema(2003)has discussed the effect of an imperfect interface on harmonic extensional wave propagation in a pre-stressed,symmetric layered composite by employing shear spring type resistance model to simulate the imperfect interface.Zhou;Lu and Chen(2012)also have tried to simulate the imperfect interface conditions by using linear spring model to study bulk wave propagation in laminated piezomagnetic and piezoelectric plates with initial stresses.Kumara and Singh(2009)have considered the propagation of plane waves at an imperfectly bonded interface of two orthotropic generalized thermoelastic rotating half-spaces with different elastic and thermal properties.Liu;Wang and Wang(2010)have analyzed SH surface waves in a piezoelectric elastic layer and an elastic half-space structure with imperfect bonding.Similar model was used by Huang and Li(2010)to study the propagation of shear waves along a weak interface of two dissimilar magnetoelectric or magnetoelectroelastic materials.Reflection and transmission problem of plane waves between piezoelectric and piezomagnetic media with imperfectly bonded interfaces has also been considered by Pang and Liu(2011).Akbarov and Ipek(2010,2012)have studied the influence of the imperfectness of the interface conditions on the dispersion of the axisymmetric longitudinal waves in the pre-strained compound cylinder under the shear spring type model of the contact condition between layers.Kepceler(2010)has also carried out investigations of a similar type for the initially stressed bi-material compounded circular cylinder.

To the best of the authors’knowledge,up to now there has not been made any investigation related to the study of the influence of imperfectness of the contact conditions on the dispersion characteristics of the generalized Rayleigh wave not only in initially stressed stratified half-space,but also in the stratified half-spaces which has not any initial stresses.Akbarov and Ozisik(2003)have studied the influence of the third order elastic constants on the velocity of the generalized Rayleigh wave propagation in a pre-stressed stratified half-plane,but they also considered only the perfect contact conditions in their analysis.So in the present work,within the framework of the second version of the small initial deformation theory of the TLTEWISB we attempt to study the effects of the imperfect interface conditions on the generalized Rayleigh wave propagation in a pre-stressed stratified half-plane.Piecewise homogeneous body model were applied and elasticity relations for materials of the constituents were described through the Murnaghan potential.In the classical sense(i.e.in the cases where the initial stresses in the constituents are absent),the investigations carried out in the present paper can be considered as a development of the paper by Tolstoy and Usdin(1953)(in which the generalized Rayleigh waves were studied for the perfectly bounded stratified half-plane)for the concrete selected pair of materials under imperfect contact between the layer and half-plane.At the same time,the investigations carried out in the present paper can be considered as a development of the paper by Akbarov and Ozisik(2003)also for the case where the contact between the constituents of the stratified half-plane is imperfect.Consequently,the goal of the investigations is a study of the role of imperfectness of the contact conditions on the dispersion characteristics of the pre-stressed bi-material non-linear elastic systems.

2　Formulation of the problem

Figure 1:The geometry of the considered stratified half-plane.

The geometry of the problem is shown in Fig.1.It is assumed that the half plane covered by the layer with thicknessh.In the natural state we determine the positions of the points by the Lagrangian coordinates which coincide with the Cartesian system of coordinatesOx1x2x3.The layer and the half-plane occupy the regions{-∞＜x1＜+∞,0≤x2≤h,-∞＜x3＜+∞}and{-∞＜x1＜+∞,-∞≤x2≤0,-∞＜x3＜+∞},respectively.Note that the following notation will be used through the formulations:the values related to the layer and half-plane are denoted by upper indices(1)and(2)respectively and the values related to the initial(or residual stresses)are denoted by upper indices(m),0 wherem=1,2.We consider the case where initial stresses in the layer and half-plane are determined as follows:

All investigations in the present paper are made in the framework of the second version of the small initial deformation theory of the TLTEWISB in the plane strain state in theOx1x2plane.

According to Guz(2004),the equations of motion for the considered case are written as:

In(2)the conventional notation is used.We assume that the following boundary conditions on the free face plane of the covering layer satisfy:

Now we consider the formulation of the imperfect contact conditions on the interface plane between the covering layer and half-plane.It should be noted that,in general,the imperfectness of the contact conditions is identified by discontinuities of the displacements and forces across the mentioned interface.A review of the mathematical modeling of the various types of incomplete contact conditions for elastodynamics problems has been detailed in a paper by Martin(1992).It follows from this paper that for most models the discontinuity of the displacement u+and force f+vectors on one side of the interface are assumed to be linearly related to the displacement u-and force f-vectors on the other side of the interface.This statement,as in the paper by Rokhlin and Wang(1991),can be presented as follows:

where C,D,G and F are three-dimensional(3×3)matrices and the square brackets indicate a jump in the corresponding quantity across the interface.Consequently,if the interface is atx2=0,then[u]=u|x2=0+-u|x2=0-,[f]=f|x2=0+-f|x2=0-.It follows from(4)that we can write incomplete contact conditions for various particular cases by selection of the matrices C,D,G and F.One such selection was made in the paper by Jones and Whitter(1967),according to which,it was assumed that C=D=G=0.In this case the following can be obtained from(4):

where F is a constant diagonal matrix.The model(5)simplifies significantly the solution procedure of the corresponding problems and is adequate in many real cases.Therefore,this model(i.e.the model(5))is called a shear-spring type resistance model and has been used in many investigations carried out within the framework of classical elastodynamics by Jones and Whitter(1967),Berger;Martin and Mc-Caffery(2000),and within the framework of the TLTEWISB by Kepceler(2010)and by Akbarov and Ipek(2010,2012).According to this statement,we also use the model(5)for the mathematical formulation of the imperfectness of the contact conditions and these conditions are written as follows:

whereFis the non-dimensional shear spring parameter and 0≤F≤∞.Note that the case whereF=0 means that the displacement component across the interface is continuous and therefore the half-space and covering layer are perfectly bonded together or to say that they are in welded contact condition.At the other extreme,F=∞implies that the half-space and covering layer are completely unbounded together and the full slipping condition is satisfied.Thus,any other finite positive values ofFexpresses different imperfect interface conditions in the problem.

Moreover,we assume that the following decay conditions are satisfied:

As stated above,we assume that the constitutive relations of the materials of the constituents are given by the Murnaghan potential which is given as follows Guz(2004):

According to Guz(2004),linearized constitutive relations for the layer and half plane materials are obtained in the following form:

3　Solution procedure and obtaining the dispersion relation

Each displacements component of the considered system are represent as follows:

We can solve the system(14)using linear operator method as follows:

or in matrix form as:

where D is the differentiation operator:D=d/d(kx2).This homogenous system(17)has non-trivial solution only when the determinant of operational matrix be zero,that is:

We determine the solution to the Eq.(20)as follows:

This dispersion equation after some mathematical manipulations can be expressed formally as follows:

The explicit expressions of theαijin the dispersion equation(23)are presented in Appendix A by formulae A1.

This completes the solution method of the problem under consideration.

4　Numerical results and discussion

We will assume that,

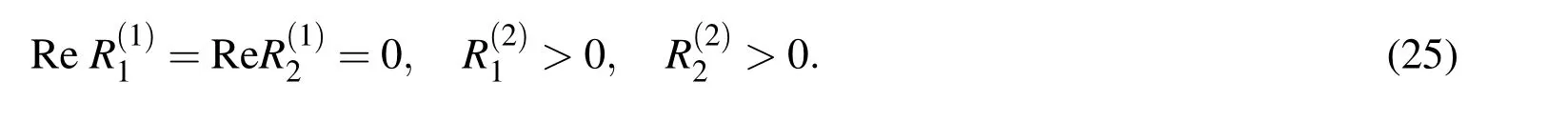
In this case,the solution(21)corresponds to such a wave propagation in the layered half-plane that the layer undergoes an oscillatory motion in theOx2direction propagating in theOx1direction with velocityc.The disturbances in the layer decay exponentially with depth in the half-plane and therefore the wave can be considered as a generalized Rayleigh wave confined to the pre-stressed covered layer[Tolstoy and Usdin(1953)].

We also,consider similar results obtained for some pairs of the real materials.Values of the mechanical constants of these materials are given in Tab.1(i.e.the values of the mechanical constants which enter the expression(8)of the Murnaghan potential).We select four pairs from these materials.For theI,II,IIIandIVpairs,the material of the covering layer we take asbronze,brass59-1,brass62 andacrylic plasticrespectively,but for all the pairs the material of the half-plane we take assteel.The graphs related to the foregoing pairs are given in Figs.3(for theIpair),4(for the pairsIIandIII)and 5(for the pairIV).Note that the results given in these figures and obtained for the case whereF=0 coincide with corresponding ones obtained in the paper by Akbarov and Ozisik(2003).

Table 1:The values of elastic constants of the selected materials[Guz(2004)].

Figure 2:Dispersion curves for Poisson material[Tolstoy and Usdin(1953)]:First and second branches of the first(a)and the second(b)modes.

Figure 3:Dispersion curves for the I pair of materials.

Thus the dispersion curves obtained for the pairsIIandIIIcoincide because,according to the data given in Tab.1,the constantsρ,λandµare the same forbrass59-1 andbrass62(Fig 4).Moreover note that,for clarity of the illustration the first and second modes of the graphs obtained for theIVpair are given separately in Figs.5a and 5b respectively.

Figure 4:Dispersion curves for the II and III pair of materials.

Figure 5:Dispersion curves for the IV pair of materials:The first and the second branches of the first(a)and the second(b)modes.

According to the well-known physical considerations,for the wave propagation velocity related to the first branch of the first mode of each pair of materials the following high wavenumber limit relation:

must satisfy,wherec(R1)is a velocity of the Rayleigh wave in the covering layer material,cSis a velocity of the Stonoley wave for the corresponding pair of materials.It is known that the Stoneley waves exist for a few pairs of materials only and do not exist for the pairs of materials selected in the present investigation.This conclusion follows from nature of the problem under consideration.Consequently,the high wavenumber limit value of the wave propagation velocity related to the first branch of the first mode of each pair of materials isc(R1).This conclusion is illustrated in Fig.6 for theIpair of materials.

Figure 6:Asymptotic behavior of dispersion curves for the I pair materials as kh→∞.

It is known that(see,Achenbach;Keshava and Hermann(1967),Akbarov and Ilhan(2008,2009),Akbarov and Salmanova(2009)and others listed therein)velocities related to the case(29)is taken as a critical velocity for a moving load acting on the free face plane of the covering layer and under this velocity of the moving load a resonance type behavior of the system takes place.Moreover,atkh=(kh)∗for which the relation(29)satisfies the group velocity becomes equal to the corresponding phase velocity and namely the velocity of the moving load which is equal to the group velocity is also called a critical velocity(see,Dieterman and Metrikine(1997)).

Now we analyze the numerical results related to the influence of the initial stresses in the constituents on the wave propagation velocity.For estimation of the magnitude of the initial stresses we introduce the parameters:

Here we will present the results only for cases:

Moreover,we introduce the notation:

for estimation of the influence of the initial stresses in the constituents,i.e.the influence of the parametersψ(1)andψ(2)on the wave propagation velocity.

Fig.8 shows that as a result of the initial stretching stress in the covering layer the wave propagation velocity related to theIIIpair of materials decreases.This conclusion was also noted in the paper by Akbarov and Ozisik(2003).In this case the imperfectness of the contact conditions,in general,causes to increase the wave propagation velocity related to the first branches of the first and the second modes.However,the imperfectness of the contact conditions before(after)a certain value of thekhcauses to decrease(increase)the wave propagation velocity related to the second branches of the first and the second modes.At the same time,it should be noted that the influence of the parameterFon the graphs betweenηandkhwhich are shown in Fig.8,has a complicate character.For instance,in the cases where 0＜kh＜3.0 the imperfectness of the contact conditions can cause to change the character of the influence of the initial stress in the covering layer on the wave propagation velocity related to the first branch of the first mode(Fig.8a).Moreover,the influence of the parameterFon the valuesηrelated to the first branch of the second mode(Fig.8b)is non-monotonic.

Now we analyze the effect of the imperfectness of the contact conditions on the influence of the initial compressional stress in the half-plane on the wave propagation velocity to theII(orIII)andIVpairs of materials in Case 2.The graphs of the dependencies betweenηandkhrelated to theII(orIII)andIVpairs of materials and constructed for various values of the parametersFandψ(2)are given in Figs.9 and 10,respectively.Note that the graphs constructed in the case whereF=0 coincide with corresponding ones obtained in the paper by

Akbarov and Ozisik(2003).It follows from the graphs given in Figs.9 and 10 that as a result of the initial compression of the half-plane the wave propagation velocity related to theII(orIII)andIVpairs of materials in Case 2 increase monotonically with the absolute values of the parameterψ(2).In this case before(after)a certain value of thekh,the influence of the parameterFcauses to increase(decrease)the wave propagation velocity related to the first branch of the first mode for theIIpair of materials.At the same time,as a result of the influence of the parameterFthe wave propagation velocities related to the second branch of the first mode,the first and second branches of the second mode of theIIpair of materials decrease.The magnitude of this decreasing depends significantly on the values of the dimensionless wavenumberkh.

Analyses of the graphs given in Figs.10a,10b and 10c show that the wave propagation velocity related to the first and second branches of the first mode and to the first branch of the second mode of theIVpair of materials decrease with the parameterF.However,the character of the influence of the parameterFon the wave propagation velocity related to the second branch of the second mode has a complicate character.This complication is also caused by decreasing of the cut off values of thekhwith the parameterF.The similar situation also takes place for the first branch of the second mode.Consequently,the influence of the imperfectness of the contact conditions on the wave propagation velocities related to the first and second branch of the second mode has not only quantitative,but also qualitative character.Moreover,the graphs given in Figs.10b and 10d show that the results obtained for the first and second branch of the second mode for various values of the parameterFcannot be limited with the corresponding ones obtained in the cases whereF=0(complete contact)andF=∞(full slipping).Note that this conclusion rises again the significance of the investigations carried out in the present paper.

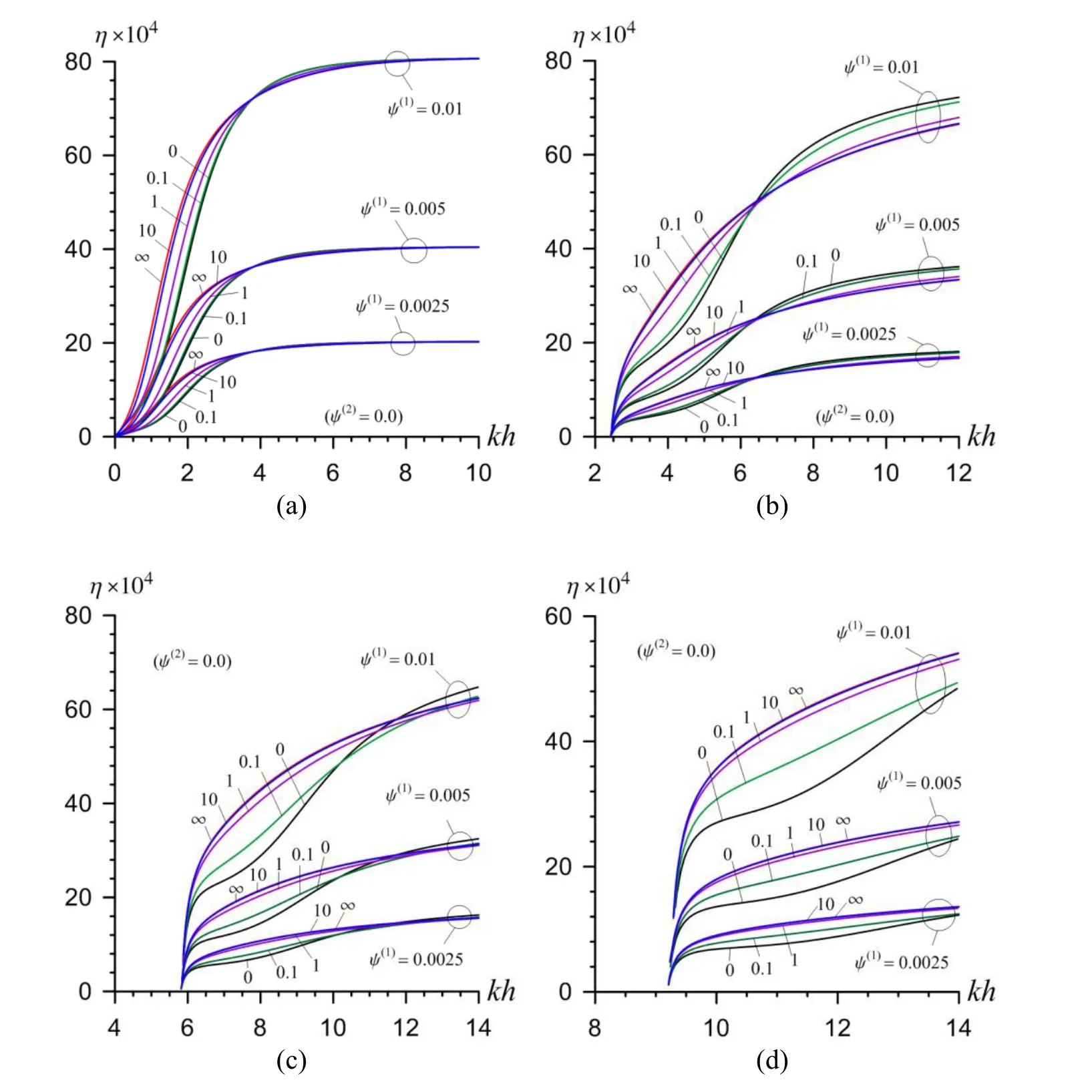
Figure 7:The influence of the imperfect bonding conditions and initial stresses to the dispersion of the generalized Rayleigh wave for the I pair of materials in Case 1:First(a)and second(c)branches of the first mode;First(b)and second(d)branches of the second mode.

Now we consider the results obtained in Case 3 for theIIpair of materials.These results are given in Fig.11 in the case whereψ(2)=-0.01 for various values of the parameterψ(1)(＞0).Note that the corresponding results obtained in the case whereψ(2)=0.0 are given in Fig.7.Consequently,it can be conclude from the comparison of the results given in Fig.11 with the corresponding ones given in Fig.7,that how the initial compression of the half-plane acts on the influence of the parameterFon the wave propagation velocities under initial stretching of the covering layer.First,this comparison shows that the initial compression of the halfplane causes to considerable increase the wave propagation velocity with respect to the wave propagation velocity obtained in the case where the initial compressionin the half-plane is absent.Moreover,this comparison shows that the influence of the parameterFon the wave propagation velocity in the latter case is more complicated than the influence of that on the wave propagation velocity obtained in the case whereψ(2)=0.At the same time,the analyses of the results given in Fig.11 shows that the graphs obtained for various values of the parameterFcannot be limited with corresponding ones obtained in the cases whereF=0andF=∞.

Figure 8:The influence of the imperfect bonding conditions and initial stresses to the dispersion of the generalized Rayleigh wave for the III pair of materials in Case 1:First(a)and second(c)branches of the first mode;First(b)and second(d)branches of the second mode.

Figure 9:The influence of the imperfect bonding conditions and initial stresses to the dispersion of the generalized Rayleigh wave for the II and III pair materials in Case 2:First(a)and second(c)branches of the first mode;First(b)and second(d)branches of the second mode.

Figure 10:The influence of the imperfect bonding conditions and initial stresses to the dispersion of the generalized Rayleigh wave for the IV pair of materials in Case 2:First(a)and second(c)branches of the first mode;First(b)and second(d)branches of the second mode.

Finally,we consider the graphs given in Fig.12 which show the dependence between theηandkhfor theIIIpair of materials in Case 4,i.e.in the case where the covering layer and half-plane are initially stretched simultaneously andψ(1)=ψ(2).Note that these graphs can be taken as generalization of the graphs given in Fig.8 for the case where the initial stretching exists not only in the covering layer,but also in the half-plane.Consequently,through the comparison of the graphs given in Fig.12 with the corresponding ones given in Fig.8 we can conclude on the action of the initial stretching of the half-plane under the influence of the initial stretching of the covering layer on the wave propagation velocity.It follows from this comparison that as a result of the initial stretching of the half plane the influence of the initial stretching of the covering layer on the wave propagation velocity related to theIIIpair of materials increase significantly and in this case the initial stretching of the covering layer causes to decrease of the wave propagation velocity.The analyses of the graphs given in Fig.12 show that the character of the influence of the parameterFon the behavior of these graphs is similar with the character of this influence on the graphs given in Fig.8.

Figure 11:The influence of the imperfect bonding conditions and initial stresses to the dispersion of the generalized Rayleigh wave for the II pair of materials in Case 3:First(a)and second(c)branches of the first mode;First(b)and second(d)branches of the second mode.

This completes the analyses of the numerical results related to the four pairs ofmaterials shown in Tab.1.Note that these results are theoretical ones.The experimental studies on the generalized Rayleigh waves for theIVpair of materials was made in a paper by Lu;Zhang and Wang(2006).These studies was carried out within the complete contact condition between the Plexiglass(Lucite)covering layer and Steel half-plane and the dispersive characteristics of Rayleigh waves are investigated experimentally.Under these studies the thickness of the covering layer is takenh=5mm(Fig.1)and the experimental results were compared with the theoretical results obtained for the first branches of the first and second modes of the dispersion curves,i.e.the experimental results are compared with the theoretical results given in Fig.5a.However,in the paper by Lu;Zhang and Wang(2006)the mentioned dispersion curves are given as graphs of dependencies between the phase velocitycand frequencyω.For clarity,in Fig.13 the dispersion curves given in Fig.5a are reconstructed as a dependencies between the phase velocitycand frequencyω.Note that,namely,the curves obtained in the case whereF=0 and given in Fig.13 were used in the paper by Lu;Zhang and Wang(2006)for verification of the experimental results and this verification illustrate a very good agreement between the theoretical and corresponding experimental results.Consequently,the experimental method used in the paper by Lu;Zhang and Wang(2006)can also be employed for verification of the theoretical results obtained for the cases whereF＞0,i.e.for verification of the imperfectness degree of the contact between covering layer and substrate.Note that the experimental methods based on the measurement of the Rayleigh waves for determination of the bonded defects in fiber-layered composites were developed in papers by Zurn and Mantell(2001)and Castaings;Hosten and Francois(2004)and others listed therein.Also,in the papers by Zurn and Mantell(2001)and Castaings;Hosten and Francois(2004)it was established that the mentioned bonded defects causes to decrease the generalized Rayleigh wave propagation velocity.Consequently,the theoretical results obtained in the present paper and related to the influence of the imperfectness of the contact conditions on the generalized Rayleigh wave propagation velocity is validated with the experimental results obtained in the papers by Zurn and Mantell(2001)and Castaings;Hosten and Francois(2004)in the qualitative sense.

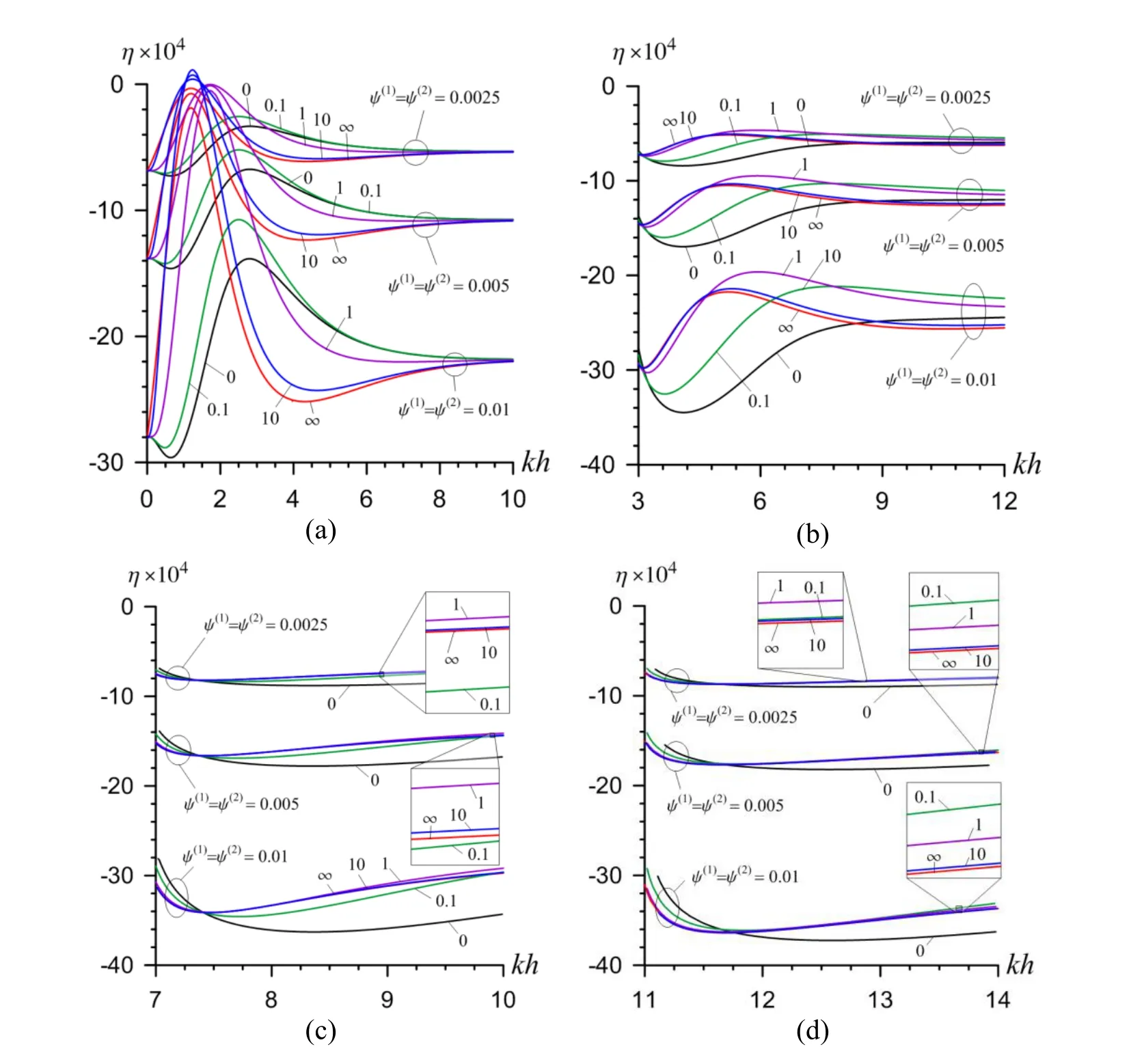
Figure 12:The influence of the imperfect bonding conditions and initial stresses to the dispersion of the generalized Rayleigh wave for the III pair of materials in Case 4:First(a)and second(c)branches of the first mode;First(b)and second(d)branches of the second mode.

Figure 13:Dispersion curves for steel half-space covered by Lucite.

Figure 14:Dispersion curves for AISI 316L stainless steel coated with vacuum plasma sprayed NiCoCrAIY.

It is known that the experimental measurement of the generalized Rayleigh wave propagation is successfully used in the non-destructive determination of the structural parameters and residual stresses in the elements of constructions.It should be noted that under these determinations alongside with experimental data the theoretical results similar with the results presented in the present paper are also used.For example,in a paper by Lakestani;Coste and Denis(1995)generalized Rayleigh waves of various frequencies were generated using a broadband pulse and their velocities were measured as a function of the frequency and compared to the theoret-ical dispersion curve of the specimen.Experiments were carried out on AISI 316L specimens coated with vacuum plasma sprayed NiCoCrAlY of various thickness(190-330µm).Fig.14 shows the dispersion curves,i.e.the dependence between the generalized Rayleigh wave propagation velocitycand the ratiohλ,wherehis a thickness of the coating andλis a wave length,obtained for the mentioned pair of materials under various values of the shear-spring type parameterF.Note that the dispersion curve constructed underF=0 and shown in Fig.14 is used in the paper by Lakestani;Coste and Denis(1995)as the theoretical results,according to which,using the experimental data the thickness of the coating is determined.Consequently,the dispersion curves obtained in the cases whereF＞0 and shownin Fig.14 can also successfully be used for determination of the imperfectness between the coating and substrate material.Moreover,the results given in Fig.15 which illustrate the influence of the initial stresses in the constituents on the wave propagation velocity of the first branch of the first mode,i.e.on the parameterη(32)in Case 1(Fig.15a),Case 2(Fig.15b),Case 3(Fig.15c)and Case 4(Fig.15d)which are determined by the expression(31),can also be used as theoretical ones for determination of the quantities of the considered type initial stresses in the coating and substrate material used under the experimental investigations carried out in the paper by Lakestani;Coste and Denis(1995).

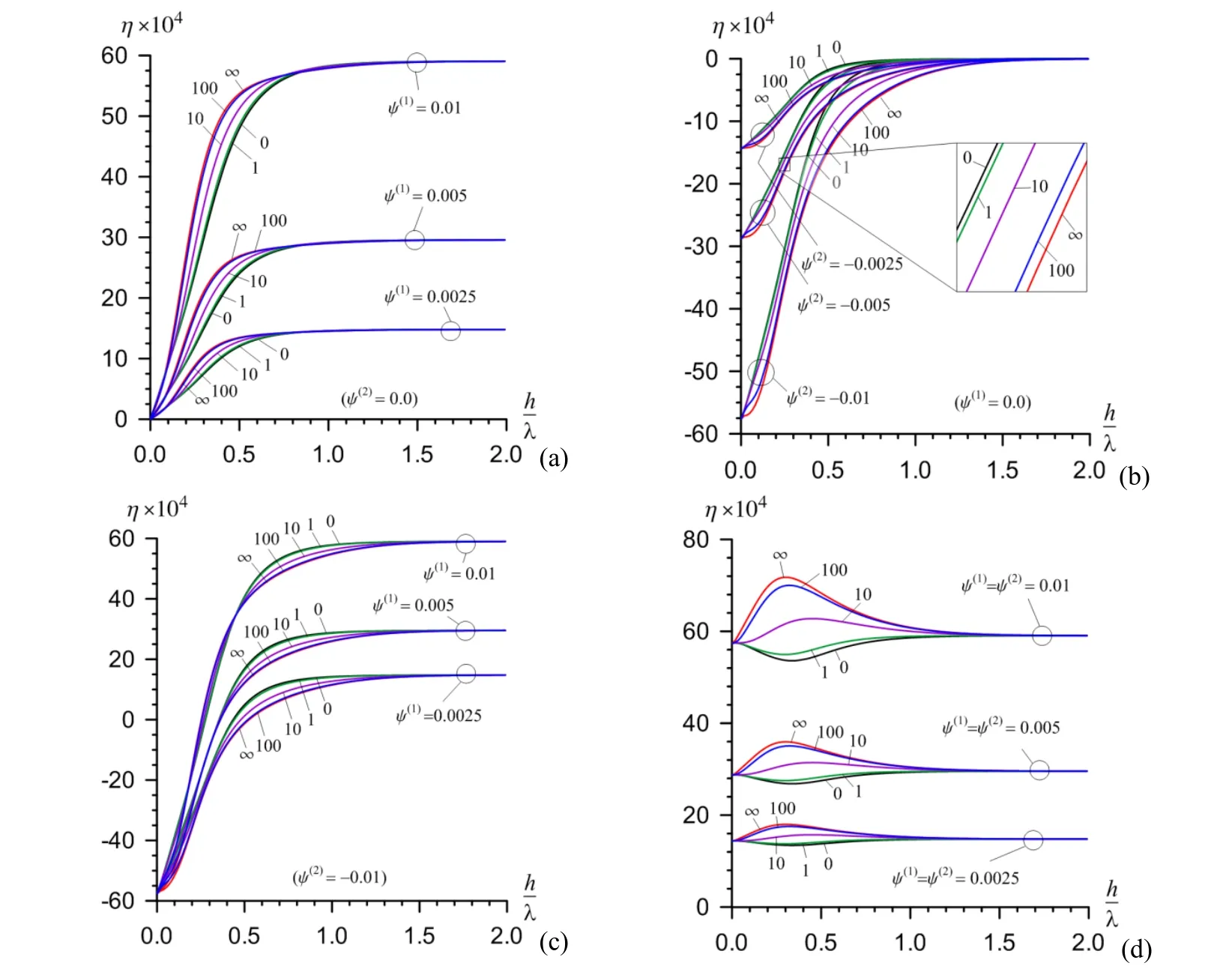
Figure 15:The influence of the imperfect bonding conditions and initial stresses to the dispersion of the generalized Rayleigh wave for AISI 316L steel coated with(VPS)NiCoCrAIY for the first branch of the first mode:(a)Case 1;(b)Case 2;(c)Case 3 and(d)Case 4.

The other application field of the generalized Rayleigh wave measurement methods is the geophysical and geotechnical engineering.This method in these engineering fields is employed for determination of the soil stiffness pro file.This pro file is constructed with an inversion process starting from the experimentally determined dispersion behavior of the Rayleigh waves.After determination of the mentioned stiffness pro file,the corresponding theoretical dispersion curves are also calculated for validation of the experimentally determined dispersion curves.Consequently,the dispersion curves constructed within the scope of the assumptions used in the present paper can also be used in the geophysical and geotechnical engineering under determination of the soil stiffness pro file.As an example,we consider the case which was considered in a paper by Foti(2002),according to which the soil is modeled as covering layer+half-plane.The thickness of the covering layer ish=10m,the densities of the covering layer and half-plane materials are equal to each other and is 1800kg/m3,shear and bulk waves velocities in the covering layer(half-plane)material are 300m/s(900m/s)and 500m/s.Fig.16 shows the graphs of dependencies between the phase velocity and frequency and these graphs relate to the first branches of the first and the second modes of the dispersion curves constructed for the above mentioned case.Note that,namely the graphs constructed in the case whereF=0 and shown in Fig.16 were used in the paper by Foti(2002)for validation of the experimentally constructed dispersion curves.Consequently the other results show in Fig.16 and obtained in the case whereF＞0 can also be used in the corresponding cases related to the geophysical and geotechnical engineering.Moreover,the results given in Fig.17,which shows the influence of the initial stresses in the soil constituents under consideration in Case 1(Fig.17a),Case 2(Fig.17b),Case 3(Fig.17c)and Case 4(Fig.17d),allows to determine the magnitude of the initial stresses in the soil layers using the experimentally constructed dispersion curves by employing the method described by Foti(2002).Note that the graphs constructed in Fig.17 relate to the first branch of the first mode.

Figure 16:Dispersion curves related to surface waves in the soil which is modeled as a covering layer+half-plane[Foti(2002)].

Figure 17:The influence of the imperfect bonding conditions and initial stresses to the surface wave dispersion in the soil which is modeled as a covering layer+half-plane[Foti(2002)].The first branch of the first mode:(a)Case 1;(b)Case 2;(c)Case 3 and(d)Case 4.

5　Conclusion

Thus,in the present paper within the framework of the piecewise homogeneous body model with the use of the second version of the small initial deformation theory of the three-dimensional linearized theory of elastic waves in initially stressed bodies the influence of the shear-spring type imperfect contact conditions on the dispersion relation of the generalized Rayleigh waves in the system consisting of the initially stressed covering layer and initially stressed half plane has been investigated.The elasticity relations of the materials of the constituents are described by the Murnaghan potential.The magnitude of the mentioned imperfectness of the contact conditions on the wave propagation velocity has been estimated through the shear-spring type parameterF(6),where 0≤F≤∞and the caseF=0(F=∞)corresponds to the complete(full slipping)contact between the constituents.Consequently,the influence of the imperfectness of the contact conditions on the generalized Rayleigh wave propagation velocity has been studied through the influence of the parameterFon this velocity.

The numerical results are obtained and discussed for the pair of the Poisson materials by Tolstoy and Usdin(1953),and four pairs of materials composed from the materials the values of the mechanic constants of which are given in Tab.1.From these discussions the following main conclusions are derived:

·The imperfectness of the contact conditions cause to decrease of the wave propagation velocity of the generalized Rayleigh waves.

·The dispersion curve constructed for each value of the parameterFis limited with corresponding ones obtained atF=0(upper limit)andF=∞(lower limit).

·The low wavenumber and high wavenumber limit values of the wave propagation velocity do not depend on the imperfectness of the contact conditions.However,the cut off values of the dimensionless wavenumberkhof the first and second branches of the second modes for the pair of materials used by Tolstoy and Usdin(1953)and for theIVpair of materials depend significantly on the parameterF.

·In the case where the complete contact conditions are satisfied between the constituents the wave propagation velocity decrease monotonically with the dimensionless wavenumberkh,however in the case where there exists the shear-spring type imperfect conditions between the constituents the dependence between the wave propagation velocity and the dimensionless wavenumberkhmay become non-monotonic for some pair of materials.Consequently,the imperfectness of the contact conditions acts on the dispersion curves and,in general,on the dynamics of the system under consideration not only quantitatively,but also qualitatively.

Note that the foregoing conclusions are made for the case where the initial stresses in the constituents are absent.In the paper the numerical results related to the action of the initial stresses in the constituents under the influence of the imperfectness parameterFon the wave propagation velocity are also presented and discussed for four pairs of materials(Tab.1).Throughout these discussions the magnitude of the initial stresses is estimated by the parametersψ(1)andψ(2)(30),and four cases indicated in(31)with respect to the signs of theψ(1)andψ(2)are considered,but the change in the values of the wave propagation velocity is estimated through the parameterη(32).We can make the following main conclusions related to the action of the parameterFon the influence of the initial stresses on the wave propagation velocity:

·The imperfectness of the contact conditions causes to increase the influence of the initial stress in the covering layer on the wave propagation velocity related to the first branch of the first mode and to the second branch of the second mode of theIpair of materials.However,the character of the effect of the imperfectness of the contact conditions,i.e.of the parameterFon the influence of the initial stress in the covering layer on the wave propagation velocity related to the second branch of the first mode and to the first branch of the second mode depends on the values of the dimensionless wavenumberkh.

·As a result of the initial compression of the half-plane the wave propagation velocity related to theII(orIII)andIVpairs of materials in Case 2 increase monotonically with the absolute values of the parameterψ(2).In this case before(after)a certain value of thekh,the influence of the parameterFcauses to increase(decrease)the wave propagation velocity related to the first branch of the first mode of theIIpair of materials.At the same time,as a result of the influence of the parameterFthe wave propagation velocities related to the second branch of the first mode,the first and second branches of the second mode of theIIpair of materials decrease.The magnitude of this decreasing depends significantly on the values of the dimensionless wavenumberkh.

·In general,the graphs of the dependence between the parametersηandkh,i.e.the influence of the initial stresses on the wave propagation velocity obtained for each value ofFcannot be limited with the corresponding ones obtained atF=0(complete contact)andF=∞(full slipping).This conclusion rises again the significance of the investigations carried out in the present paper.

·Numerical results obtained for theIVpair of materials under complete contact conditions are validated with the corresponding experimental ones which were detailed in the paper by Lu;Zhang and Wang(2006).

·The character of the influence of the imperfectness of the contact between the covering layer and half plane on the generalized Rayleigh wave propagation velocity in the qualitative sense is validated with the experimental ones given by Zurn and Mantell(2001)and Castaings;Hosten and Francois(2004).

·Dispersion curves for the pair of materials considered in the paper by Lakestani;Coste and Denis(1995)are also obtained and the possible application of the numerical results under determination of the structural parameters and residual stresses in the coated materials is proposed.

·The possible application of the numerical results which are similar to the obtained ones and relate to the determination of the soil structure and stiffness in the geophysical and geotechnical engineering is also discussed and corresponding numerical results are presented for the case considered in the paper by Foti(2002).

Many other details of the results obtained for the initially stressed cases are discussed in the text of the paper.

Appendix A:

The expressions of the componentsαij(i;j=1,2,3,4,5,6)in(23)are:

Achenbach,J.D.;Keshava,S.P.;Hermann,G.(1967):Moving load on a plate resting on an elastic half-space.Journal of Applied Mechanics,vol.34,no.4,pp.910-914.

Akbarov,S.D.;Ozisik,M.(2003):The influence of the third order elastic constants to the generalized Rayleigh wave dispersion in a pre-stressed stratified halfplane.International Journal of Engineering Sciences,vol.41,pp.2047-2061.

Akbarov,S.D.(2007):Recent investigations on the dynamical problems of the elastic body with initial(residual)stresses(review).International Applied Mechanics,vol.43,no.12,pp.3-27.

Akbarov,S.D.;Ilhan,N.(2008):Dynamics ofa system comprising an orthotropic layer and pre-stressed orthotropic half-plane under the action of a moving load.International Journal of Solids and Structures,vol.45,pp.4222-4235.

Akbarov,S.D.;Ilhan,N.(2009):Dynamic sofa system comprising an orthotropic layer and pre-stressed orthotropic half-plane under the action of an oscillating moving load.International Journal of Solids and Structures,vol.46,pp.3873-3881.

Akbarov,S.D.;Salmanova,K.A.(2009):On the dynamics of a finite pre-strained bi-layered slab resting on a rigid foundation under the action of an oscillating moving load.Journal of Sound and Vibration,vol.327,pp.454-472.

Akbarov,S.D.;Ipek,C.(2010):The influence of the imperfectness of the interface conditions on the dispersion of the axisymmetric longitudinal waves in the pre-strained compound cylinder.CMES:Computer Modeling in Engineering and Sciences,vol.70,no.2,pp.93-121.

Akbarov,S.D.;Agasiyev,E.R.;Zamanov,A.D.(2011):Wave propagation in a pre-strained compressible elastic sandwich plate.European Journal of Mechanics A/Solids,vol.30,pp.409-422.

Akbarov,S.D.(2012):The influence of third order elastic constants on axisymmetric wave propagation velocity in the two-layered pre-stressed hollow cylinder.CMC:Computers,Materials&Continua,vol.32,no.1,pp.29-60.

Akbarov,S.D.;Ipek,C.(2012):Dispersion of axisymmetric longitudinal waves in the pre-strained imperfectly bonded bi-layered hollow cylinder.CMC:Computers,Materials&Continua,vol.30,no.2,pp.99-144.

Berger,J.R.;Martin,P.A.;McCaffery,S.J.(2000):Time-harmonic torsional waves in a composite cylinder with an imperfect interface.Journal of the Acoustical Society of America,vol.107,no.3.pp.1161-1167.

Biot,M.A.(1965):Mechanics of incremental deformations:Theory of elasticity and viscoelasticity of initially stressed solids and fluids,including thermodynamic foundations and applications to finite strain.John Wiley&Sons.

Castaings,M.;Hosten,B.;Francois,D.(2004):The sensitivity of surface guided modes to the bond quality between a concrete block and a composite plate.Ultrasonics,vol.42,pp.1067-1071.

Dieterman,H.A.;Metrikine,A.(1997):Critical velocities of a harmonic load moving uniformly along an elastic layer.Journal of Applied Mechanics:ASME,vol.64,pp.596-600.

Eringen,A.C.;Suhubi,E.S.(1975):Elastodynamics,Volume I,Finite Motions,Academic Press.

Eringen,A.C.;Suhubi,E.S.(1975):Volume II,Linear Theory,Academic Press.

Foti,S.(2002):Numerical and experimental comparison between two-station and multistation methods for spectral analysis of surface waves.Rivista Italiana di Geotecnica,vol.1,pp.11-22.

Guz,A.N.(2002):Elastic waves in bodies with initial(residual)stresses.International Applied Mechanics,vol.38,no.1,pp.23-59.

Guz,A.N.(2004):ElasticwavesinBodieswithInitial(Residual)Stresses,“A.S.K”,Kiev,(in Russian).

Guz,A.N.(2005):On foundations of the ultrasonic non-destructive method of determination of stresses in near-the-surface layers of solid bodies.CMES:Computer Modeling in Engineering and Sciences,vol.8,no.3,pp.217-230.

Huang,Y.;Li,X.F.(2010):Shear waves guided by the imperfect interface of two magnetoelectric materials.Ultrasonics,vol.50,pp.750-757.

Jones,J.P.;Whitter,J.S.(1967):Waves at a flexibly bonded interface.Journal of Applied Mechanics,vol.34,pp.905-909.

Kepceler,T.(2010):Torsional wave dispersion relations in a pre-stressed bi-material compounded cylinder with an imperfect interface.Applied Mathematical Modeling,vol.34,pp.4058-4073.

Kumara R.;Singh,M.(2009):Effect of rotation and imperfection on reflection and transmission of plane waves in an isotropic generalized thermoelastic media.Journal of Sound and Vibration,vol.324,pp.773-797.

Lakestani,F.;Coste,J.F.;Denis,R.(1995):Application of ultrasonic Rayleigh waves to thickness measurement of metallic coatings.NDT&T International,vol.28,no.3,pp.171-178.

Leungvichcharoen,S.;Wijeyewickrema,Anil C.(2003):Dispersion effects of extensional waves in pre-stressed imperfectly bonded incompressible elastic layered composites.Wave Motion,vol.38,pp.311-325.

Liu,J.;Wang,Y.;Wang,B.(2010):Propagation of Shear Horizontal Surface Waves in a Layered Piezoelectric Half-Space With an Imperfect Interface.IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,vol.57,no.8,pp.1875-1879.

Lu,L.Y.;Zhang,B.X.;Wang,C.H.(2006):Experimental and inversion studies on Rayleigh wave considering higher modes.Chines Journal of Geophysics,vol.49,no.4,pp.974-985.

Martin,P.A.(1992):Boundary integral equations for the scattering of elastic waves by elastic inclusions with thin interface layers.Journal of Nondestructive Evaluation,vol.11,pp.167-174.

Pang,Y.;Liu,J.X.(2011):Reflection and transmission of plane waves at an imperfectly bonded interface between piezoelectric and piezomagnetic media.European Journal of Mechanics A/Solids,vol.30,pp.731-740.

Pecorari,C.(2001):Scattering of a Rayleigh wave by a surface-breaking crack with faces in partial contact.Wave Motion,vol.33,pp.259-270.

Rokhlin,S.I.;Wang,Y.J.(1991):Analysis of boundary conditions for elastic wave interaction with an interface between two solids.Journal of the Acoustical Society of America,vol.89,pp.503-515.

Tolstoy,I.;Usdin,E.(1953):Dispersive Properties of Stratified Elastic and Liquid Media:A Ray Theory.Geophysics,vol.18,pp.844-870.

Truestell,C.(1961):General and exact theory of waves in finite elastic strain.Archive for Rational Mechanics and Analyses,vol.8,no.1,pp.263-296.

Zhou,Y.Y.;Lü,C.F.;Chen,W.Q.(2012):Bulk wave propagation in layered piezomagnetic/piezoelectric plates with initial stresses or interface imperfections.Composite Structures,vol.94,pp.2736-2745.

Zurn,B.;Mantell,S.C.(2001):Nondestructive evaluation of laminated composites using Rayleigh waves.Journal of Composite Materials,vol.35,no.12,pp.1026-1044.