基于Hamilton 体系对燃料电池烧结变形的分析

罗淇任，张劲夫

（西北工业大学， 710072）

0 前言

由于固体氧化物燃料电池的阳极、电解质、阴极结构中各层的热膨胀系数不一样，在制造过程中，当温度从烧结温度降低至室温时，会造成热应力和翘曲。为了缓解这种现象，必需发展合适的材料和优化设计电池组以便使它们能够承受热机械的工作量而不产生裂纹。因此复合材料得到了广泛应用。

工程实践中将大量用到复合材料层合板结构，而起横向剪切变形的影响将越来越重要而不能被忽略。复合材料力学研究的一项重要课题就是复合材料热应力分析。文献[1]推导了各向异性热弹性体的基本方程，文献[2]等研究了耦合热弹性问题的一般解。

在弹性力学中Hamilton 体系有着非常重要的作用。文献[3]给出波动方程周期性问题的辛差分算法。文献[4]则导出了条形域平面弹性问题的Hamilton 体系及其本征解。文献[5，6]从三维弹性力学的基本方程出发，建立了Hamilton 正则方程的一般形式。

本文在层合板的热应力分析之中引入Hamilton 体系，在一阶层合板理论的基础上，建立了以一个空间方向为展开方向的Hamilton 正则方程。在辛几何数学框架下，采取共轭辛正交关系给出层合板热应力的辛精确解。

1 层合板热应力问题的基本方程和横向本征问题.

一阶层合板理论的平衡方程为.

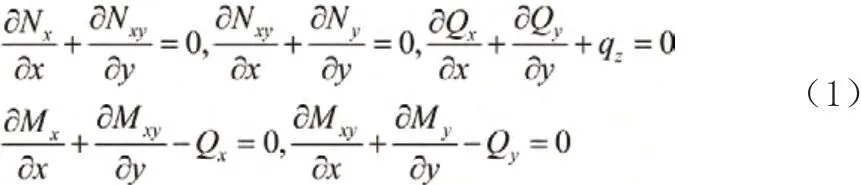
其中有

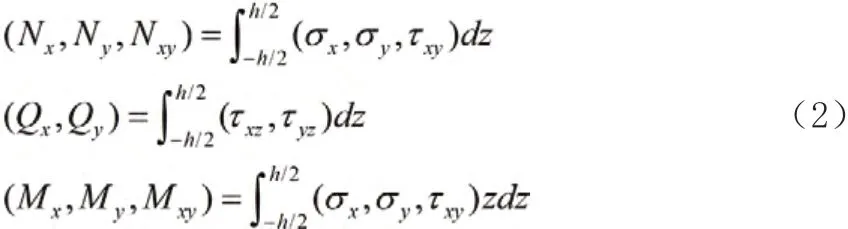
层合板的总厚度为H。在温度载荷作用下，层合板的本构方程为

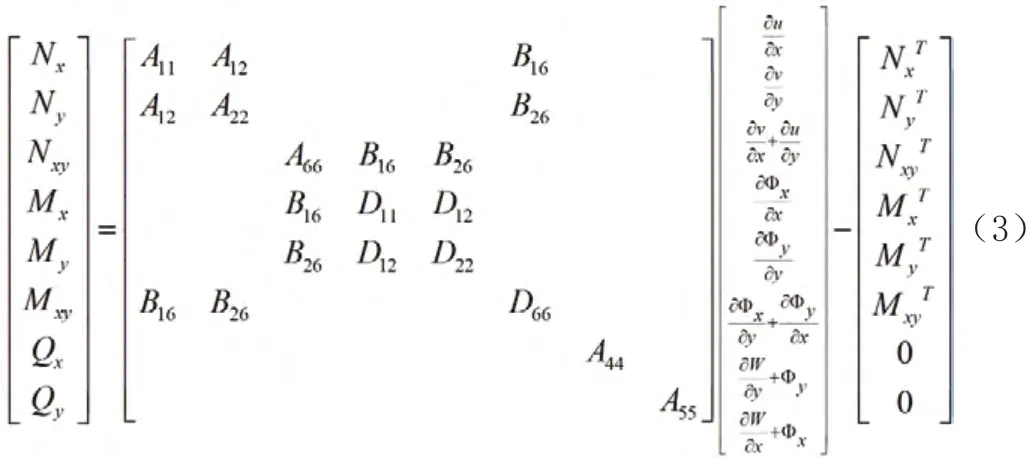
其中

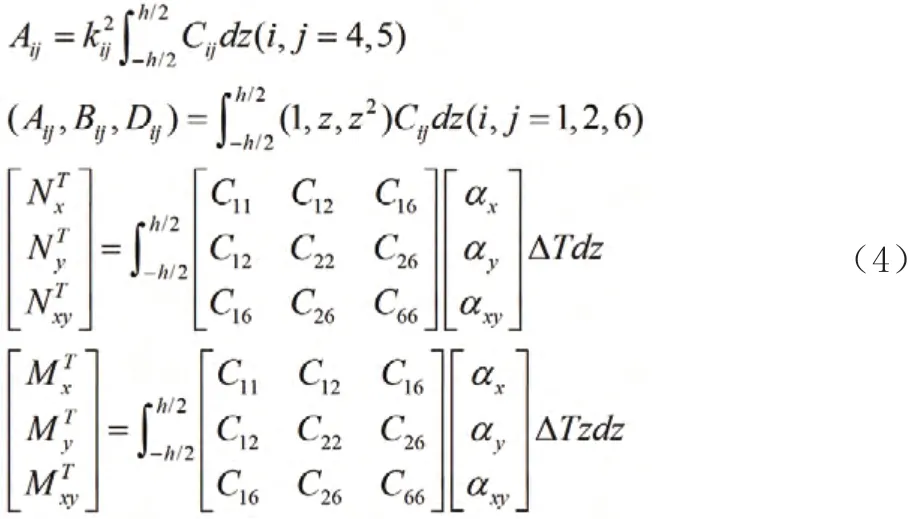
将坐标y 模拟时间以建立Hamilton 体系，选择状态变量为

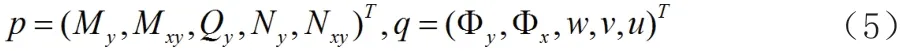
得到层合板热应力分析的Hamilton 正则方程

其中F，C，K 的表达式见附录。

H 为Hamilton 算子矩阵，再引入辛几何度量矩阵.

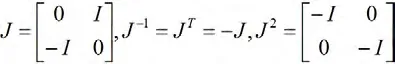
2 共轭辛正交解法

考虑x 轴对边简支的矩形层合板，它的边界条件为

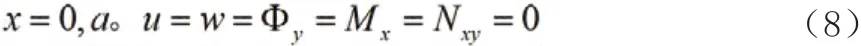
除此之外还要考虑交界面位移连续条件及力的平衡条件

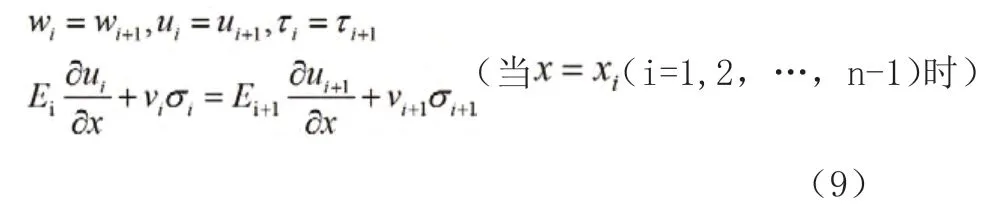
考虑正则方程的齐次解

采用分离变量法[4].，拉维型全状态变量假设为

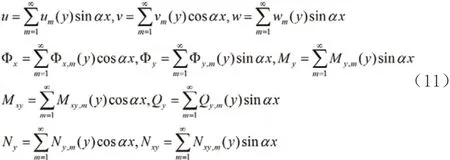
将（11）式代回（6）式，变为如下形式

设下标i，j 分别表示为（12）的两个本征解，则有

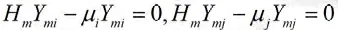
将上面两式联立得到

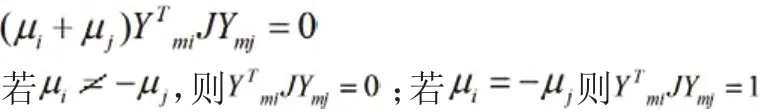
这说明对于全部的满足式（8），（9）的全状态向量是不会线性相关的，它们构成有限维空间的基底，所以任一状态向量展开为

将其代回（12）得到

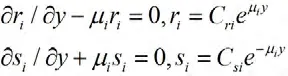
则有

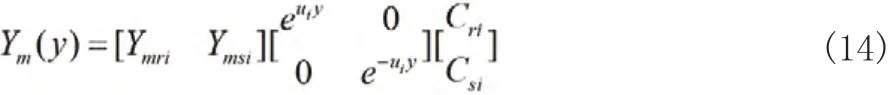
代回到（12）得到

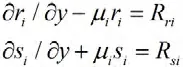
解得

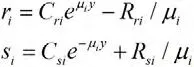
这样得到全状态变量的通解为

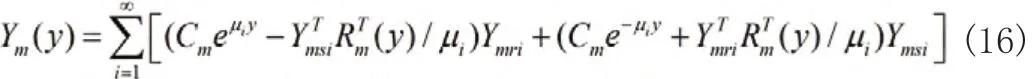
3 数值算例

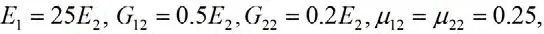
4 结束语

将Hamilton 体系导入到层合板热应力的分析中，所提供的解严格满足问题的微分方程，边界条件以及层间位移连续性条件和应力平衡条件。

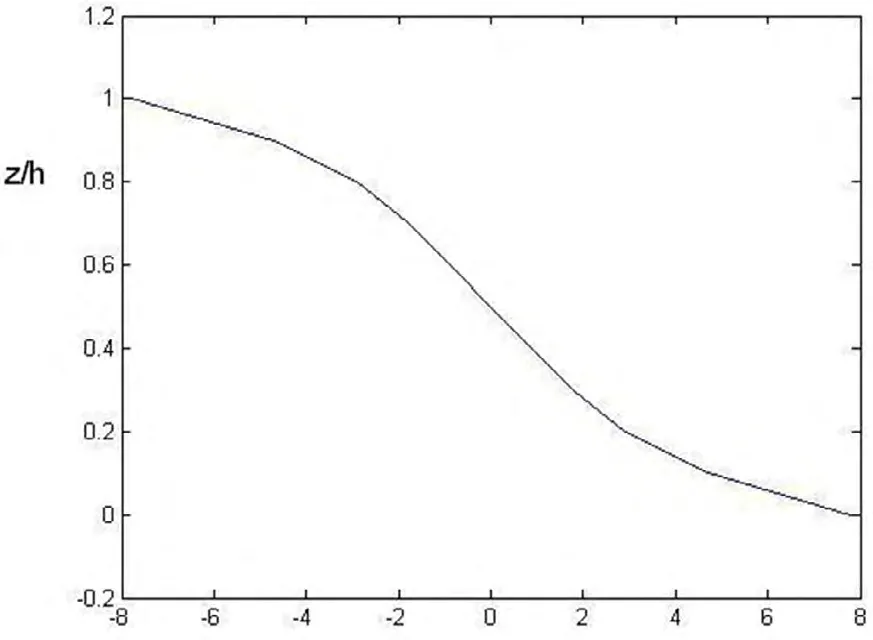
沿着厚度上的（0，b/2）的分布

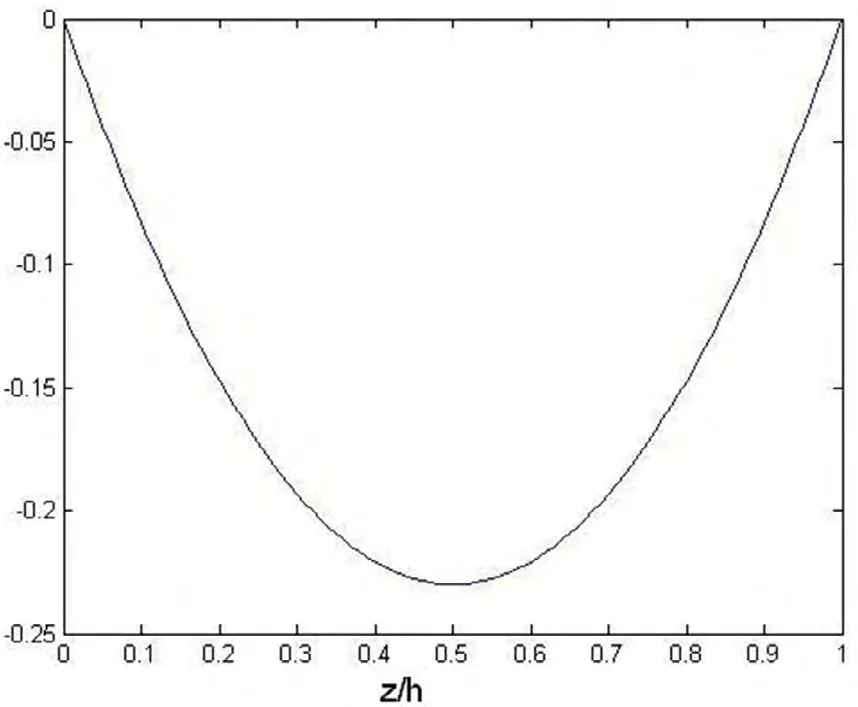
沿着厚度上的(a/2,b/2)的分布

[1] Ting T C T.Anisotropic elasticity theoy and applications[M].New York, Oxford University Press, 1996.506-507

[2] 丁皓江，国风林，侯鹏飞。耦合热弹性问题的一般解[J]，应用数学和力学，2000，21（6）：573-577

[3] 冯康，泰孟兆。Hamilton 动力体系的Hamilton 算法，自然科学进展一国家重点实验室通讯，1991，（2）：104-112

[4] 钟万勰。条形域平面弹性问题与哈密顿体系。大连理工大学学报，1991，31（4）：373-384

[5] 唐立民。弹性力学的混合方程和Hamilton 正则方程。计算结构力学及其应用。1991，8（4）：433-450

[6] 邹贵平，唐立民。各向异形弹性力学问题Hamilton 正则方程的一般形式，计算结果力学及其应用。1994，11（2）：140-146

[7] Tauchert T R.Thermally induced flexure, buckling and vibration of plates.Appl.Mech.Rev.1991,44(8):347-359

[8] 邹贵平。反对称铺设层合板动力问题的Hamilton 体系及辛几何解法。固体力学学报。1996，17（4）：312-319

附录

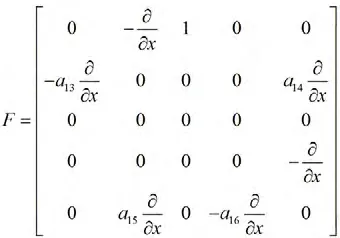
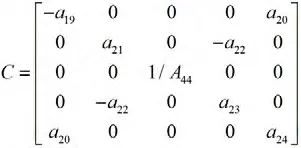
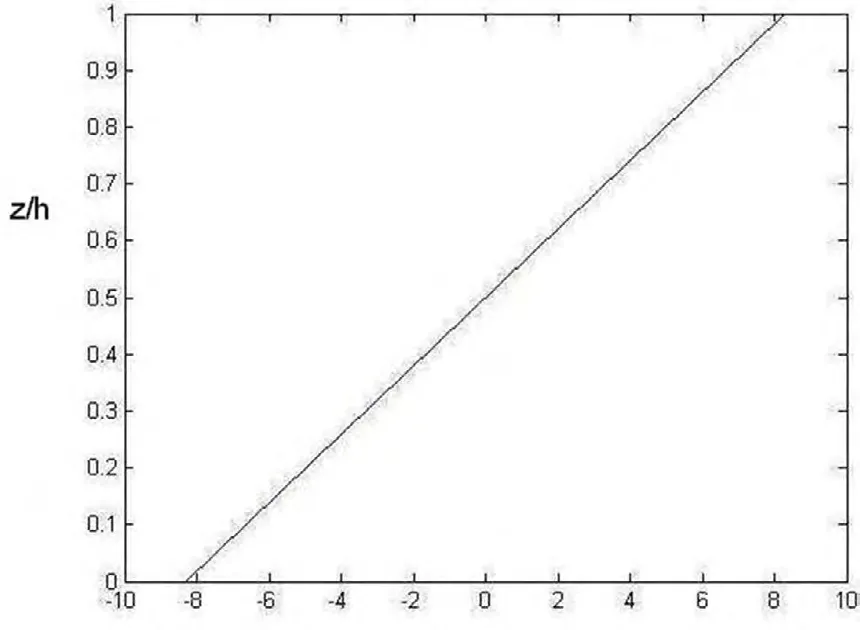
沿着厚度上的(0,0)的分布

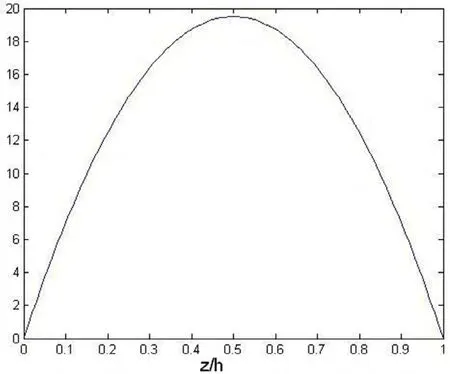
沿着厚度上的(0,b/2)的分布