基于量块的步距规测量及不确定度分析

钱丰，丁少文，孙玉玖，

(1.中航工业北京长城计量测试技术研究所，北京100095;2.中航工业陕西飞机工业集团有限公司机械动力分公司，陕西西安710089)

0 引言

步距规是通过一系列测量面构成的、高精度的、稳定的多值实物标准器。生产步距规时，按照一定的排列方式将多个标准平行块固定于基体上，由各标准平行块工作面提供一系列的同向和异向标准尺寸。由于步距规相对传统的长度标准器量块，拥有多值和便携的特点，因此已被越来越多地应用于数控机床、三坐标测量机的检验和校准［1］。

国内大区实验室一般采用坐标测量机配合双频激光干涉仪进行步距规的校准，英国、日本、澳大利亚等国家计量院也采用类似方法［2-3］，但此种方法需要使用高准确度仪器，测量成本较高。本文提出了一种使用电感测微仪在平板上与量块比较测量步距规的方法，该方法使用量块、电感测微仪、平板、表架等常见仪器设备，仪器通用性强，同时有效地控制了成本。

1 测量方法

测量用计量器具及配套设备见表1所示。

表1 测量用计量器具及配套设备

测量步距规的具体步骤如下:

1)选取尺寸与步距规上标称值一致的量块。100 mm 以下尺寸可以直接选取单一量块，100 mm 以上尺寸由一个100 mm 倍数尺寸的量块和一个100 mm 以下尺寸的量块拼合而成。将量块和步距规置于平板上恒定4 h，将电感测微仪置于分辨力0.01 μm 档。

2)将组合量块和步距规需要测量的平面对齐，将电感测微仪球形测头置于组合量块的工作面中心，将电感测微仪读数置0，见图1。

图1 电感测微仪对零示意图

3)平稳平移组合量块，使量块离开球形测头。平稳平移步距规，使球形测头置于步距规被测平面(上工作面)中心，读取电感测微仪读数A1，见图2。

图2 步距规测量示意图

4)计算组合量块的偏差B1，步距规被测平面的偏差值C1按公式(1)进行计算。有

5)其他各点偏差Cn依次按步骤1)～4)进行测量和计算。

2 测量不确定度分析

2.1 不确定度的来源

为保证测量结果真实可靠，组合量块一般不超过2块。假设量块与步距规均为钢制，膨胀系数为(11.5±1)×10-6℃-1;量块、步距规、电感测微仪、平板在实验室恒定24 h 以上，实验室温度为(20±0.3)℃。

测量中可能引入不确定度的来源有:①量块存在偏差值且研合量块存在间隙;②电感测微仪存在示值误差和示值变动性;③量块的膨胀系数存在一定的误差;④量块和步距规的温度差;⑤量块和步距规之间存在线膨胀系数差;⑥步距规的温度对20 °C 会有偏离;⑦步距规各个工作面对底面存在平行度误差;⑧量块的长度变动量造成测量点位置不一致;⑨步距规底面的平面度会造成步距规的倾斜;⑩平板的局部平面度会造成测量点位置不一致;⑪测量重复性和仪器分辨力。

2.2 标准不确定度评定

2.2.1 由标准器(量块)引入的测量不确定度

以校准步距规990 mm 点为例进行分析评估。假设标准器由900 mm 和90 mm 两块二等量块拼合而成。

二等量块偏差值［4］的测量不确定度U=0.05 μm +0.5×10-6L，假定其符合t 分布，k=2.62。则偏差值引入的不确定度分量为

u11=0.10 μm/2.62=0.038 μm

u12=0.50 μm/2.62=0.191 μm

组合量块中间存在研合层［4］，假定研合层厚度在20 nm 范围内变化，假定其符合均匀分布，，则拼合间隙引入的不确定度分量为

引入各不确定度分量的因素互相独立，则当使用二等量块作为标准器时，量块引入的测量不确定度u1为

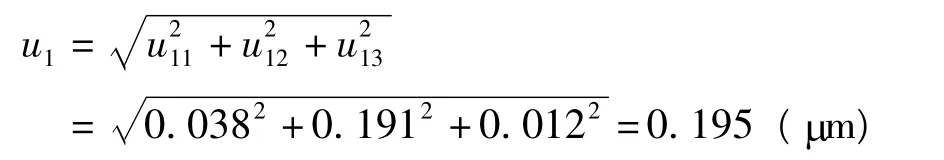
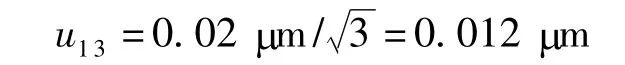
2.2.2 由电感测微仪引入的测量不确定度

0.01 μm 档电感测微仪的最大允许误差［5］为±0.08 μm，假定其符合均匀分布，，则电感测微仪的示值误差引入的不确定度分量为

电感测微仪的示值变动性［5］(9 次测量最大最小值的差值)为0.03 μm，用极差法计算重复性，s=0.03/2.9=0.01 μm。示值变动性的影响由测量量块和测量步距规的差构成，因此引入的不确定度分量为

引入各不确定度分量的因素互相独立，则电感测微仪引入的测量不确定度u2为

2.2.3 由量块膨胀系数引入的测量不确定度

量块和步距规在测量前已经放置在仪器上充分定温，温度差约为0，则该项测量不确定度可以忽略不计。

2.2.4 由量块和步距规温度差引入的测量不确定度

量块和步距规温度差为±0.04℃，假定其在该范围内符合均匀分布，，则由量块和步距规温度差引入的不确定度分量为

u3=L×11.5×10-6×0.04/1.732

=0.266×10-6L

=0.266×10-6×990 mm=0.263 μm

2.2.5 由量块和步距规膨胀系数差引入的测量不确定度

假设990 mm 的步距规和量块均为钢制，膨胀系数为α=(11.5±1)×10-6℃-1，则两者最大的差值可能为2×10-6℃-1，假定其符合三角分布，，则由膨胀系数引入的不确定度分量为

2.2.6 由步距规的温度偏差引入的测量不确定度

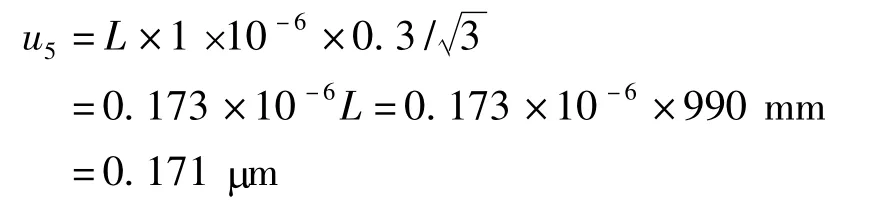
2.2.7 由步距规测量点的位置引入的测量不确定度

测量点可以控制在直径1 mm 的范围内，测量点对步距规被测块中心的最大偏离以0.5 mm 估计，工作尺寸变动量在4 mm×4 mm 范围内定义，步距规的工作尺寸变动量以最大值发生在一边方向上估计。0 级步距规［6］的工作尺寸变动量满足0.5 μm +1.3×10-6L，假定其在该范围符合均匀分布，，则引入的不确定度分量为

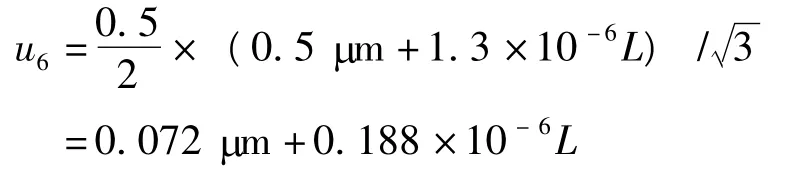
当L=990 mm 时，u6=0.228 μm。

2.2.8 由量块测量点的位置引入的测量不确定度

测量点可以控制在直径1mm 的范围内，测量点对量块中心的最大偏离以0.5 mm 估计，研合量块的长度变动量以最大值发生在短边并且方向一致的方向上估计，2 等量块长度变动量最大为0.1 μm +0.3×10-6L，假定其在该范围内均匀分布，，测量时取2 次平均值，则引入的不确定度分量为

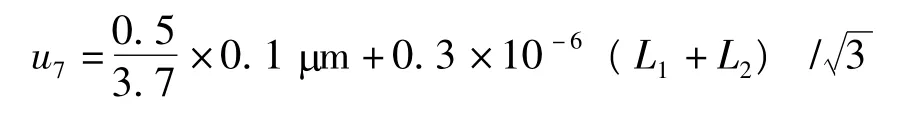
当L=990 mm 时，u7=0.039 μm。

2.2.9 步距规倾斜引入的测量不确定度

步距规底面的平面度等会造成步距规的倾斜，在平板不同位置对步距规同一位置进行测量试验，测量长度为1000 mm 时的变化量为0.2 μm，假定其在该范围内均匀分布，，则引入的不确定度分量为

当L=990 mm 时，u8=0.114 μm。

2.2.10 平板的局部平面度引入的测量不确定度

通过试验，获得平板平面度影响在0.15 μm，假定其在该范围内均匀分布，，且对步距规和量块同时影响，则引入的不确定度分量为

2.2.11 测量重复性或仪器分辨力引入的测量不确定度

对步距规在1000 mm 的测量点进行连续测量，记录读数分别为:0.18，0.22，0.33，0.26，0.22，0.33，0.31，0.18，0.24，0.29 μm。利用贝塞尔公式计算标准差为

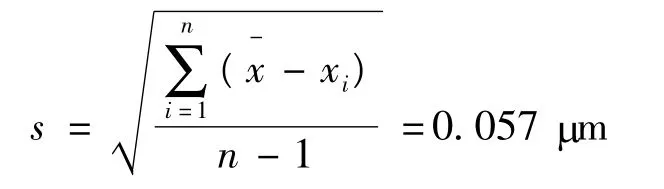
电感测微仪的分辨力为0.01 μm，远小于测量重复性的影响。实际测量时，读数由量块和步距规读数差构成，因此取测量重复性为测量重复性或仪器分辨力引入的标准不确定度分量，即

2.3 合成标准不确定度

由于引入以上各项标准不确定度分量的因素之间没有值得考虑的相关性［7］，则合成标准不确定度为

2.4 扩展不确定度

取包含因子k=2，则扩展不确定度

U=0.542 μm×2=1.1 μm

2.5 其他测量点测量不确定度

考虑到研和用的2 块量块中较小的一块尺寸为10 ～90 mm，因此，选取最小、最大、中间尺寸(即10，90，50 mm)进行分析，更有代表性。可以计算各个校准点的测量不确定度(k=2)，见表2。

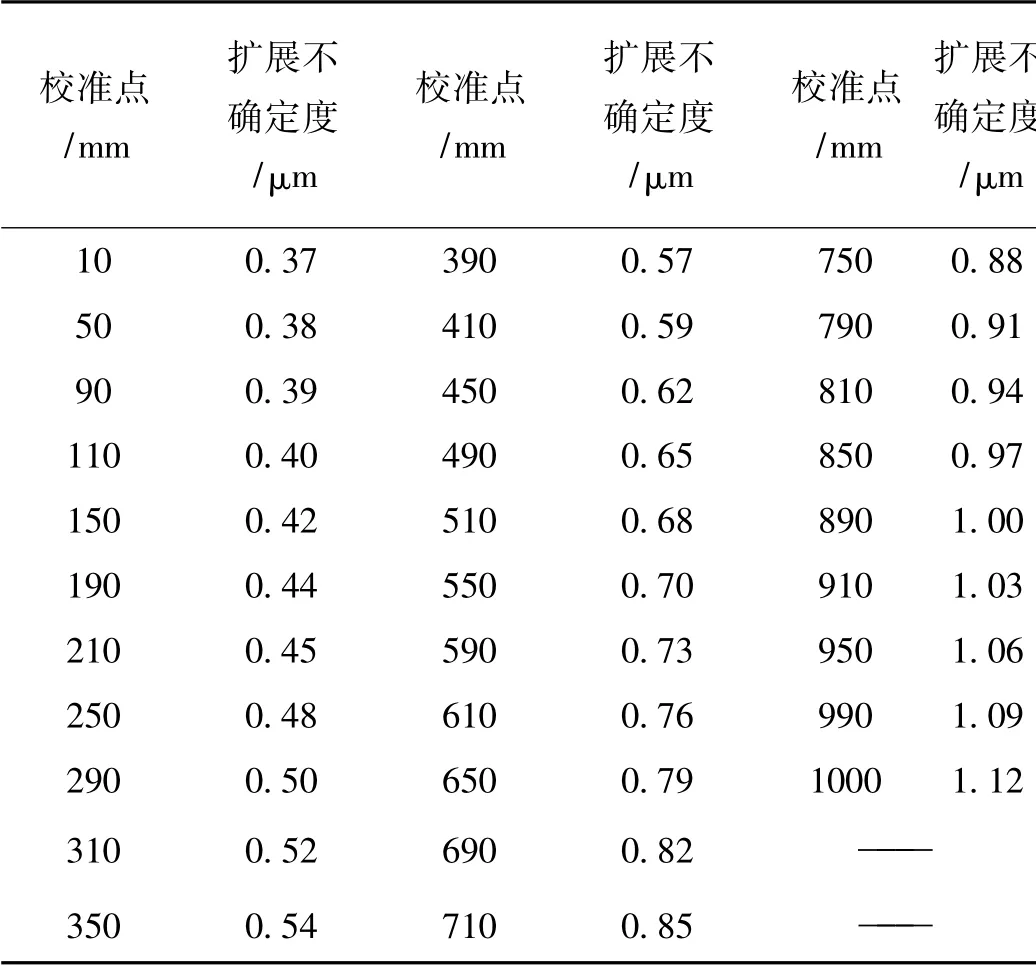
表2 各个校准点的测量不确定度(k=2)明细表

综上，当使用二等量块做测量标准，实验室温度控制在(20±0.3)℃时，测量步距规尺寸偏差的扩展测量不确定度近似可表示为

U=0.4 μm+0.8×10-6L(k=2)

同理，经分析计算，当使用三等量块做测量标准，实验室温度控制在(20±0.5)℃时，测量不确定度近似为

U=0.4 μm +1.2×10-6L(k=2)

3 与其他常见测量方法比较

常见的校准方法［8］有:激光干涉仪和坐标测量机结合的校准方法(方法1)，坐标测量机直接校准方法(方法2)，光学灵敏杠杆与激光干涉仪结合直接校准方法(方法3)。本方法使用电感测微仪和量块比较校准，与其它3 种方法的比较见表3。

由表3 可见，本方法在仪器成本不高的同时可以达到较小的测量不确定度。

4 总结

本文介绍了一种基于量块和电感测微仪的步距规校准方法。该方法的优点是可以利用现有条件(量块、电感测微仪、表架、平板)，使用较少的成本，达到较小的测量不确定度。缺点是该方法耗费时间;同时由于研合量块需要一定经验，因此对计量人员的操作水平有较高要求;且只能应用于底工作面为研磨面的步距规的测量，有一定局限性。因此，在没有专用测量仪器时，本方法可用于步距规的校准。

表3 测量步距规方法优缺点比较表

［1］国家质量监督检验检疫总局.JJF 1258-2010 步距规校准规范［S］.北京:中国计量出版社，2010.

［2］Sonko Osawa，Toshiyuki Takatsuji，Tomizo KUROSAWA.Step-Gauge calibration using an interferometric coordinate measuring machine and the uncertainty［C］//Proceedings of the XVII IMEKO World Congress.Dubrovnik，Croatia:IMEKO，2003 :1191-1194.

［3］Tae Bong Eom，JinWan Han.A precision length measuring system for a variety of linear artifacts［J］.Measurement Science and Technology，2001(12):698-701.

［4］国家质量监督检验检疫总局.JJG 146-2003 量块检定规程［S］.北京:中国计量出版社，2003.

［5］国家质量监督检验检疫总局.JJF 1331-2011 电感测微仪校准规范［S］.北京:中国质检出版社，2011.

［6］工业和信息化部.JB/T 10977-2010 步距规［S］.北京:机械工业出版社，2010.

［7］国家质量监督检验检疫总局.JJF 1059.1-2012 测量不确定度评定与表示［S］.北京:中国质检出版社，2013.

［8］晏浩.步距规的校准方法［J］.计量技术，2006(2):21-22.