基于MEMS陀螺的低成本捷联惯导系统设计
2014-04-13何海洋王章波
何海洋,王章波
(中国空空导弹研究院,河南洛阳471009)
0 引言
与传统的基于光纤或激光陀螺的捷联惯性导航系统相比,MEMS 陀螺具有很高的成本优势,随着技术的不断进步,MEMS 惯性器件的性能也在不断提升,当前MEMS 陀螺的性能已达到中等精度,能满足航空、航天、军事等领域的使用要求。
本文所设计的基于MEMS 陀螺和石英挠性加速度计的低成本捷联惯性导航系统(SINS),具有体积小、成本低、可靠性高、精度适中的特点,适用于低成本战术武器导航和制导系统。在战术武器中通常采用SINS/GPS 组合导航作为其导航手段,GPS 导航系统虽然能够提供精确的位置、速度信号,但在动态环境中其可靠性差,且易受到干扰而变得不可使用,过分依赖卫星导航系统存在隐患。捷联惯导系统具有动态性能好、短期精度高等优点[1],且不受外部干扰、完全自主的工作,所以精度适宜的低成本捷联惯导系统可为这类低成本战术武器提供可靠的导航与制导能力,具有重要的军事应用价值。
1 捷联惯导系统硬件设计
根据国内惯性器件研制现状,综合考虑成本与性能要求设计的低成本捷联惯导系统硬件主要包括三轴MEMS 陀螺组合;三轴石英挠性加速度计组合;温度传感器;信号采集处理电路和导航计算机。其结构框图如图1所示。SINS 的核心部件是惯性测量单元(IMU)。IMU 由陀螺仪和加速度计以及外围电路组成,陀螺仪测量弹体角运动,加速度计测量弹体线运动,其误差是导航系统误差的主要来源之一,其精度直接决定了导航精度[2]。
图1 中,三个正交配置的石英挠性加速度计和三个正交配置的MEMS 陀螺直接安装在弹体上,惯性传感器输出弹体相对于惯性空间的角速度和线加速度,通过专用接口电路数字转换后送到导航计算机中。利用标定后形成的误差补偿参数,对惯性器件的测量值进行误差补偿,使用补偿后的角测量信息,获得由弹体坐标系到导航坐标系的坐标变换矩阵;用计算出的姿态矩阵对加速度测量信号进行坐标变换,将它们变换到导航坐标系上,再经过积分,即可得到导弹相对于导航坐标系的速度和位置。惯性导航系统利用这些信息和其他信息形成制导及飞行控制信号。

图1 捷联惯导系统硬件框图
2 惯性传感器件
MEMS 陀螺仪是以微机械工艺为基础制作的惯性仪表,与传统惯性元件相比,具有体积小、质量轻、功耗小、成本低、易集成、抗过载能力强和可批量生产等特点,具有广泛的应用前景。
目前,国内MEMS 陀螺的研制已相对比较成熟,可生产补偿后全温漂移在100(°)/h 左右的陀螺,价格也较低。国内的MEMS 加速度计还在发展之中,实测精度较低,而石英挠性加速度计已广泛应用于航空、航天、航海及武器系统的导航制导与控制中,精度较高,价格适中,故采用小型化的中精度石英挠性加速度计。
3 陀螺仪、加速度计信号检测及处理电路
陀螺输出的信号滤掉高频干扰后,通过电阻转变为电流,进入积分器,积分器的输出进入A/D 模数变换器,A/D 变换器以固定的采样时间对积分器的输出电压进行采样,输出的数字信号进入DSP 数字信号处理器作插值的处理,再除以时间间隔,即可求出积分器输出的斜率,此斜率正比于陀螺输出的电压,DSP运算所得的陀螺角速率的符号和绝对值送给CPLD,即可得到脉冲串,单位时间内的脉冲串与陀螺转速成正比。脉冲串经过隔离、宽度调整以及整形后通过射极输出。
加速度计输出电流较小,采用I/F 变换电路将其输出转换为表征速度增量的脉冲信号。I/F 变换器采用了全电流有源积分式、浮动地单恒流源变换方式。电路由放大器、变换器和同步器三部分组成。放大器和变换器都是由三通道电路构成的,可同时处理三个通道上的加速度信号;同步电路用来处理来自三个通道的脉冲频率信号,以保证各通道信号的同步。
在小型捷联惯导系统中,为降低功耗和体积,一般不采用恒温温控装置,但需对惯性器件的零偏、标度因数非线性和安装误差建立温度补偿模型,利用温度传感器精确测量惯性器件的实际温度,温度的测量结果以二进制形式由飞控计算机读取,实时补偿惯性器件因温度产生的误差,以提高角速度和加速度通道的实际使用精度。
4 导航计算机
导航计算机需要在短时间内不断地进行惯导解算、误差补偿、信息融合等大量的计算,同时又要与外部系统通信、时序逻辑控制等工作,这要求计算机的处理器具有很高的运算速度。为此我们选用浮点DSP +FPGA 模式,考虑到捷联式惯性导航算法的复杂性和耗时性,且运算量很大,需建立“数学平台”以代替平台惯导的机械平台[3]。为满足系统实时性的要求,DSP 采用32 位浮点TMS320C2812,惯导解算部分不超过2 ms,可以满足速度要求,选用ACTEL 的A54SX08系列FPGA 完成采集、控制与通信等功能。
5 导航算法编排
MEMS 陀螺仪和石英挠性加速度计直接固联在弹体上,通过导航计算机依靠算法建立导航坐标系,即平台坐标系以数学平台的形式存在,省略了复杂的机械平台。
导航坐标系选发射时刻的当地地理坐标系,发射后导航坐标系与发射点的当地地理坐标系固连。
6 惯性器件误差补偿算法
由于陀螺和加速度计的零偏和标度因数都是温度的函数,通过对陀螺和加速度计的输出量进行静态误差及动态误差补偿,可以提高惯性元件的实际使用精度[4]。
MEMS 陀螺的模型方程如下

式中:ωgx,ωgy,ωgz为按补偿模型方程算出的陀螺仪的输出;Kgx(T),Kgy(T),Kgz(T)为陀螺的标度因数函数,主要与温度T 有关;Ngx,Ngy,Ngz为采样周期ts内陀螺输出脉冲数;Dgx(T),Dgy(T),Dgz(T)为陀螺的常值漂移函数,主要与温度T 有关;εgx,εgy,εgz为陀螺随机漂移;Egxy,Egxz,Egyx,Egyz,Egzx,Egzy为陀螺各轴的安装误差角。
石英挠性加速度计的模型方程如下

式中:Aax,Aay,Aaz为按补偿模型方程算出的加速度计的输出;Kax(T),Kay(T),Kaz(T)为加速度计标度因数函数,主要与温度T 有关;Nax,Nay,Naz为采样周期ts内加速度计输出脉冲数;Dax(T),Day(T),Daz(T)为加速度计的零位偏置函数,主要与温度T 有关;εax,εay,εaz为加速度计的随机误差;Eaxy,Eaxz,Eayx,Eayz,Eazx,Eazy为加速度计各轴的安装误差角。
使用带温箱的三轴转台在全温范围内通过六位置法对IMU 进行静态和速率标定,利用标定所得的各项误差系数,通过计算机对误差实施有效的补偿,可以有效提高IMU 的实际使用准确度。
7 姿态解算
姿态算法求解弹体坐标系到导航坐标系之间的坐标转换矩阵。姿态矩阵的解算精度直接影响制导精度。在此我们选择等效旋转矢量法的二子样算法。
7.1 等效旋转矢量的计算
假定在 [t,t+Δt ]的时间间隔内,陀螺输出角增量在 [t,t+Δt/2 ]和 [t+Δt/2,t+Δt ]时,分别为θ1和θ2,根据二子样算法,等效旋转矢量为
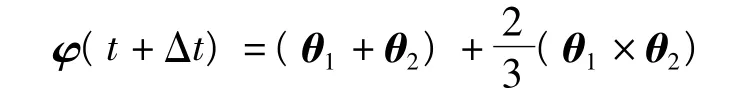
式中:φ=[φx,φy,φz]T表示惯导系统某一时刻的等效旋转矢量矩阵;φx,φy,φz表示x,y,z 陀螺输出的角增量。
7.2 姿态四元数的即时更新
利用等效旋转矢量计算姿态四元数,根据四元数的定义,四元数定时增量q(Δt)对应于在一定时间间隔内发生的转动。利用q(Δt)去修正基准四元数Q(t),被修正的四元数Q(t+Δt)由四元数的“乘积”给出
Q(t+Δt)=q(Δt)·Q(t)
式中:φ0=(φ·φ)1/2。把sin(φ0/2)和cos(φ0/2)展开成级数,考虑系统精度和计算量要求,取四阶即可。
7.3 四元数的规范化
为了保证通过四元数计算的姿态矩阵是正交矩阵,需要对姿态四元数进行规范化处理,以消除由于算法上的截断误差和计算机的舍入误差所造成的影响,对于四元数仅需归一化处理。
Q=Q0+Q1i+Q2j+Q3k

其中,i=0,1,2,3。
7.4 姿态矩阵更新及姿态角计算
导航坐标系用n 表示,其坐标原点位于地平系,X,Y,Z 轴对应指向北、天、东;弹体坐标系用b 表示,其坐标原点位于弹体质心,X,Y,Z 轴对应指向弹前、上、右。则姿态矩阵为

根据姿态矩阵和姿态角的对应关系,可得横滚角γ、偏航角ψ、俯仰角θ 分别为
γ=-atan2(T23,T22)
ψ=-atan2(T31,T11)
θ=-asin(T21)
8 速度位置的计算
导航坐标系中基本导航方程为

在计算周期Δt 内对上式两边积分,得
Vn(t+Δt)=Vn(t)+ΔVn(t)
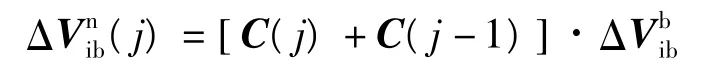

9 试验结果及分析
为了测定所设计的低成本捷联式惯性导航系统的性能,进行了大量的静态高低温试验。考虑到该系统与GPS 组合进行导航,仅对系统前60 s 测试数据进行分析。图2,3,4 是样机在常温下经过60 s 的静态测试所得的结果。由于是静态测试,给定的初始横滚角γ、俯仰角ψ、俯仰角θ 均为0°;给定的导航系三个轴向初始速度均匀为0 m/s,三个轴向初始位置均为0 m。

图2 SINS 静态姿态角变化曲线

图3 SINS 静态速度变化曲线
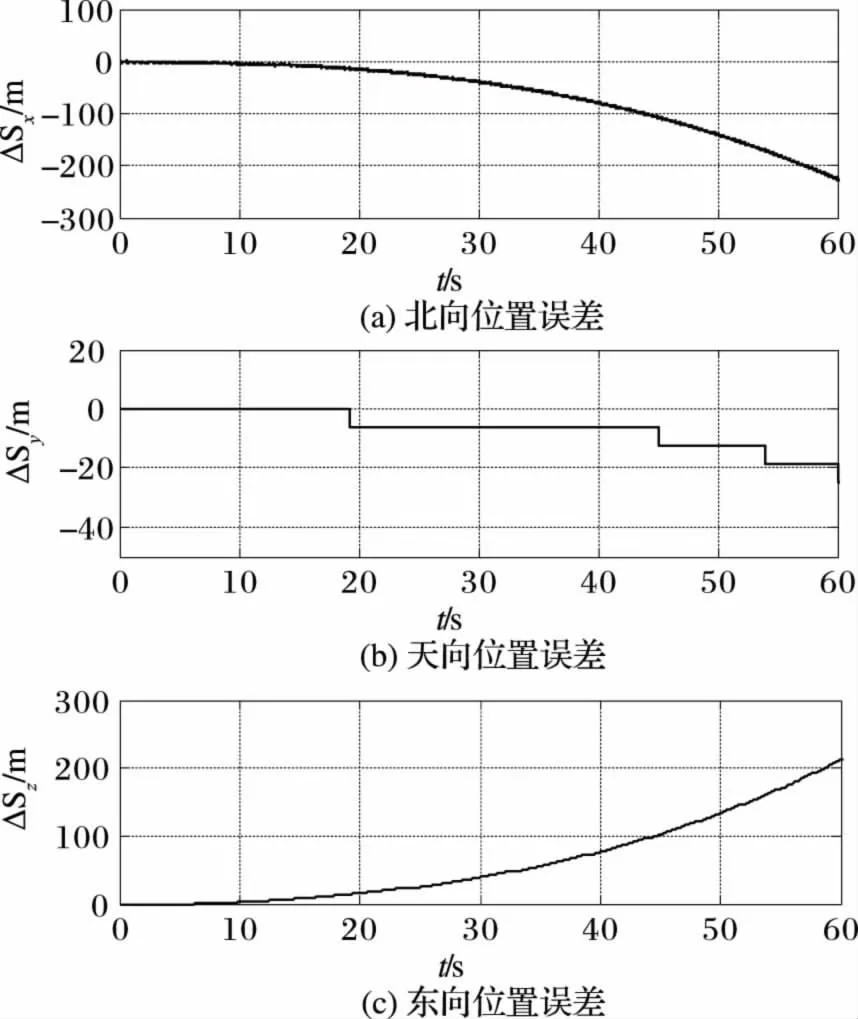
图4 SINS 静态位置变化曲线
通过试验结果可以看出,捷联惯导得到的导航参数随时间发散,这是惯性导航系统的固有特性。样机静态测试60 s,姿态误差为1.3°,速度误差为9 m/s,位置误差为220 m,在较短的时间内(<20 s),系统纯惯性导航结果良好,基本达到设计要求,可以满足SINS/GPS 组合导航系统需求。
10 结论
本文根据工程实际应用背景,设计了基于MEMS陀螺和石英挠性加速度计的低成本捷联惯性导航系统。通过IMU 测试标定、误差补偿,样机试验结果可知,此系统短时间(<20 s)准确度较高,稳定性好,能够满足GPS 短期失效条件下,组合导航系统导航定位的要求。
[1]付相松,高社生,张学渊.基于MEMS 技术车载组合导航研究[J].计算机测量与控制,2009,17(2):338-340.
[2]熊智,刘建业,林雪原,等.激光陀螺捷联惯导系统中惯性器件误差补偿技术[J].上海交通大学学报,2003,37(11):1287-1288.
[3]邓正隆.惯性技术[M].哈尔滨:哈尔滨工业大学出版社,2006.
[4]司宏源,庞秀芝,鲁浩.捷联惯性测量装置全温度标定方法[J].电光与控制,2007,(6):127-130.
