动静组合加载条件岩爆特性及倾向性指标

殷志强 ，李夕兵，董陇军，金解放，马海峰

(1. 安徽理工大学 深部煤矿采动响应与灾害防控安徽省重点实验室，安徽 淮南，232001；2. 中南大学 资源与安全工程学院，湖南 长沙，410083；3. 中国矿业大学(北京) 资源与安全工程学院，北京，100083)

深部岩体开挖工程受高地应力及开挖扰动共同作用，极易诱发岩爆等动力灾害。岩爆的发生对深部岩体开挖工程造成极大的影响，严重时造成生产中断、设备毁坏，并对生产人员的生命安全带来很大威胁[1-2]。岩爆的发生受开挖岩体本身力学性质、应力、岩体弹性能量储存及释放等众多因素共同影响决定[3]。因此从岩体本身力学性质出发，通过大量现场及实验室力学实验对深部开挖岩体能否发生岩爆进行预先判断，探讨岩爆发生机理，是预防岩爆灾害的基础，并已成为岩爆研究的重要途径[4]。针对实验设备及方法的不同，国内外研究学者开展广泛的岩爆特性研究[5]并提出相应的岩爆倾向性指标。Kidbinski[6]通过开展岩石加卸载实验，利用实验过程卸载释放的弹性应变能与耗损的弹性应变能之比，提出岩石的弹性变形能指数，认为其比值越大岩爆倾向性越高；Goodman[7]在刚性试验机上开展岩石的全应力-应变实验，根据所得全应力-应变曲线，定义峰值前应力-应变曲线下面积与峰值后应力-应变曲线下面积之比，提出岩石冲击能指标，认为峰值前岩石变形积累的能量较峰值后岩石破坏所需的能量越大，其岩爆倾向性越明显；Saito[8]针对Kan-Etsu 隧道导洞中岩爆段与非岩爆段的岩样开展全应力-应变实验，在峰后应力区实验分别得到非稳定破裂传播的Ⅱ型破坏曲线和稳定破裂传播的Ⅰ型破坏曲线，并指出曲线类型与岩样破坏形式之间具有重要的相关性；唐礼忠等[9]通过分析典型的大理岩加卸载及全应力-应变曲线，根据岩石在变形和破坏过程中的能量变化，提出用剩余能量指数表征岩石的能量储存与能量耗散的相对关系，并由此作为岩爆倾向性指标。目前较多针对静态或准静态条件下的本源型岩爆来表征岩爆特性及倾向性指标研究。当进入深部岩体开挖时，开挖岩体承受高地应力、开挖卸荷、强动力扰动耦合作用，此种情况下产生的岩爆，显然是岩体在动静组合载荷下发生的力学行为之一，表现为激励型岩爆。因此，对动静组合加载下岩爆特性研究更具有现实意义。

1 动静组合加载实验

1.1 试样制备

试样由同块完整性和均匀性相对较好的砂岩加工而成，试样为圆柱体，直径×高为50 mm×50 mm。试样两端面进行仔细打磨，其不平行度和不垂直度均小于0.02 mm[10]。试样静载物理力学性能见表1。

表1 砂岩静载物理力学性能Table 1 Physico-mechanical properties of sandstone under static loads

1.2 实验设备

为模拟深部开挖岩石所对应的地应力、开挖卸荷、动力扰动多场耦合受力特性，基于SHPB 试验系统进行改进[11-12]，改进后的三轴动静组合试验系统，如图1 所示。经改进可以加载与冲击载荷方向垂直的围压。在围压和轴向静压加载设备处设有液压阀门，压力加载之后，可通过手动控制阀门开闭大小，控制压力卸载速率。入射杆、透射杆及冲头最大直径均为50 mm，对试样进行等径冲击加载。

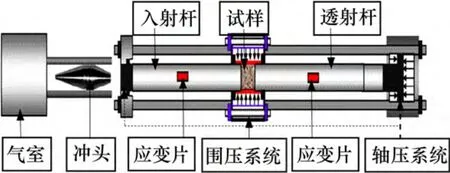
图1 基于SHPB 装置的三维动静组合加载系统示意图Fig.1 Sketch of triaxial SHPB coupled static and dynamic loads

1.3 实验方案

冲击试验中共进行常规动态压缩试验和动静组合加载试验2 种，动静组合加载试验中轴向静压共取5 个级别，分别为0，18，54，63 和72 MPa，约相当于静载抗压强度的0，20%，60%，70%和80%，结果如图2 所示。试样两端面涂抹适量黄油，确保试样两端面与入射杆和透射杆间接触良好。应力加载时预先由手动加载轴、围压。加载时以相同加载速度加载轴向静压和围压(40 MPa)，保持轴向静压不变，围压以1 MPa/s 的速率卸载至0 MPa(手动控制)，并移除围压装置。实验过程中严格保证冲头冲程相同，以保证在相同气压冲击下施加的冲击载荷的一致性。实验时以试样刚好呈现宏观破裂面造成整体破坏，为试样临界破坏[13]冲击能量；然后逐步增加冲击气压，每次提高0.1 MPa 气压，提高冲击能量，共进行5 组不同冲击能量试样。

图2 常规抗压试验应力-应变曲线Fig.2 Stress-strain curve in static compression test

2 动静组合加载实验结果分析

2.1 实验应力-应变曲线特性

图3 所示为试样在不同轴压水平不同冲击扰动能量下具有代表性的冲击试验应力-应变曲线。由图3可以看出：在较低静载(0，18 MPa)动静组合实验中所得应力-应变曲线普遍为I 型，随冲击能量的增加其变化趋势类似，均呈现峰值应力逐渐增大且峰后应变逐渐增加的变化趋势；当轴向静载较大时(63，72 MPa)，应力-应变曲线随冲击能量的增加，峰后应变有明显变化，即由临界破坏时峰后应变发生回弹现象的Ⅱ型曲线逐渐转变为无峰后应变回弹的Ⅰ型曲线。由此可见动静组合加载条件下砂岩试样冲击应力-应变曲线明显受轴向应力的影响，尤其在较小冲击能量的动力扰动引起试样临界破坏时，如图3(f)所示。

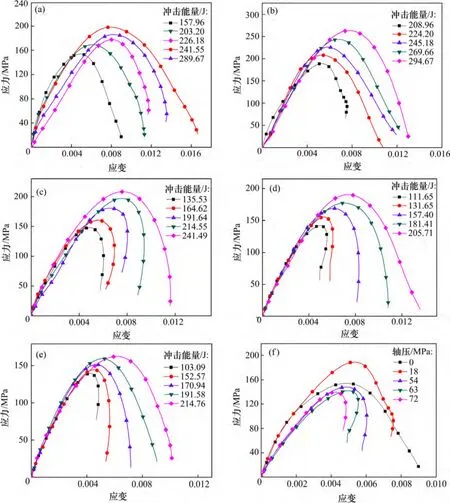
图3 冲击实验应力-应变曲线Fig.3 Stress-strain curves in dynamic tests

本文实验中所施加的最大轴向静载为试样单轴抗压强度的70%左右，一般认为在单轴抗压强度70%及以下的应力加载情况下，试样处于压密及典型的弹性变形阶段，试样内储存大量弹性应变能[14]，由此可见较高的轴向静载所带来的较大弹性应变储能，在较小冲击加载下，对试样的破坏变形，尤其是峰后变形阶段有明显的影响。

2.2 试样破坏特征及能耗规律

由图3 可以看出：当轴向静载为63 MPa 时，其应力-应变曲线具有典型的Ⅱ型曲线和Ⅰ型曲线。结合其应力-应变曲线，图4 所示为该轴向静载时不同入射能量下的试样破坏形态。

图4 不同入射能量下的试样破碎形态Fig.4 Failure modes of sample under different incident energy

从图4 并结合图3(d)中对应的应力-应变曲线可以看出，当入射能量较小时，其应力-应变曲线表现为较典型的Ⅱ型曲线，试样仅发生部分破坏，试样内部呈现“X”形压剪型破裂面，并近似形成以透射杆端部位为底的圆锥形破裂，主要破坏发生在试样表面部分岩块的破裂和剥落[15]，试样主体仍具有一定的承载能力；当如射能量逐渐增大时，其应力-应变曲线逐渐表现为较典型的Ⅰ型曲线，此时试样无大块保留，整体失稳，完全失去承载能力，形成大小不一的碎块和大量岩粉。

计算实验过程作用在试样上的入射能、反射能及透射能，得到不同动静组合加载条件下的单位体积能量消耗[16]，结果如图5 所示。

图5 动静组合加载下试样能耗密度Fig.5 Density of energy under coupled static and dynamic loads

图5 中试样单位体积能耗密与冲击能量的关系，得出单位体积能耗随冲击能量增大呈现增加的趋势；随轴向静载的增加，砂岩试样临界破坏能耗由正值逐渐转变为负值，轴向静压为0 MPa 和18 MPa 时，砂岩试样冲击破坏能耗密度均为正值；当轴向静压增大到54，63 和72 MPa 时，砂岩试样在较低冲击能量加载下破坏能耗密度为负值。

当轴向静压为0 MPa 时，试样无应力作用；轴向静压为18 MPa 时，由图2 可以看出：18 MPa 的轴压试样处于试样压密段状态，故这2 种轴压条件下试样均无弹性应力能量的存储和释放，其对应的应力-应变曲线为典型的Ⅰ型曲线，试样破坏过程均为体现出吸收冲击扰动能量。随轴向静压逐渐增大时，由于试样在冲击加载破坏前具有一定的弹性应变能量储存，在受冲击扰动造成试样破坏时将以一定形式释放出来，当冲击扰动较小时，试样破程度较小，试样破坏能耗整体体现为负值，同时应力-应变曲线相应呈现出典型的Ⅱ型曲线，随冲击能量的增大，岩石试样破碎程度增大，需要更多的能量消耗在破碎所需的表面能，需要消耗部分外部冲击扰动能量，故能耗逐渐转变为正值，同样 应力-应变曲线由典型的Ⅱ型曲线逐步转变为Ⅰ型曲线。

综合考虑文献[8]的结论：当试样破坏时得到Ⅱ型曲线，则认为此时发生岩爆现象；及从在许多发生过岩爆的现成工程中观察发现，发生岩爆的地段并没有完全丧失承载能力，仍保持一定的稳定状态的现象[17]；以及岩爆过程为能量释放过程的认识。因此，在轴向静压为63 MPa 时，较低入射能量(111.65 J)下试样的破坏为典型的实验室岩爆现象，在较高入射能量作用下，试样虽然破坏更为猛烈，但其破坏主要为外界动力导致，因此不是岩爆现象。

由此可见：动静组合加载实验所得Ⅱ型应力-应变曲线，能反映出试样受静应力和冲击扰动共同作用下岩爆发生的倾向性。

3 动静组合加载岩爆倾向性指标

3.1 动静组合加载岩爆倾向性指标

根据Goodman 和Saito 岩爆能量冲击性指标Wcf计算方法：

式中： φsa为岩石应力峰值强度前储存的能量； φsc为应力峰后消耗的能量。

由式(1)对本文试样不同加载条件下所得应力-应变曲线进行计算，可以求得试样的能量冲击性指标Wcf，所得指标与冲击加载入射能量的关系如图6 所示。由图6 可以看出：砂岩试样在常规动态冲击实验和较低静载的动静组合加载实验时，其Wcf指标值一般为1～2 之间，且规律性不明显。而在承受较高静载荷的动静组合实验中，当冲击能量小于180 J 时，其能量冲击性指标值较高，一般大于2，整体呈现出一定的规律性：随入射能量的增加，能量冲击性指标值呈现随之降低。但在轴向静载55 MPa 和65 MPa 时，部分能量冲击性指标值出现与此规律相反的现象。如轴向静压65 MPa 中能量最小的2 个数据结果及55 MPa 中间能量段的几个数据结果，与该现象的数据点相对应的应力-应变曲线，均为较典型的Ⅱ型曲线。可以看出单独以 φsa/φsc为岩爆倾向性指标，在Ⅱ型曲线时所得岩爆倾向性出现异常结果。

图6 能量冲击性指标Wcf 与入射能量的关系Fig.6 Relationships between incident and Wcf

结合Goodman 和Saito 研究成果，本文提出一种基于可以体现Ⅱ型曲线能量释放的特点，表征岩石在动静组合加载下岩爆倾向性的指标DS。定义为：

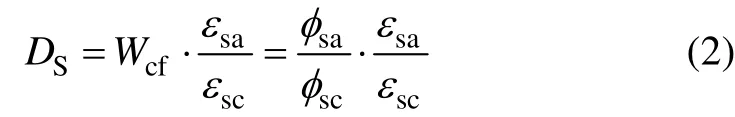
式中：εsa为应力峰值前应变；εsc应力峰值后总应变。各参量见图7。

图7 应力-应变曲线下DS 指标中各参量示意图Fig.7 Sketches of several parameters in index DS of stress-strain curves

采用 φsa/φsc与 εsa/εsc的乘积的形式，综合考虑弹性应变能量储存、释放及相应的应变因素，以期消除现有岩爆倾向性指标的不足，并可以同时对Ⅰ型和Ⅱ型应力-应变曲线进行岩爆倾向性进行判别。

当应力-应变曲线为Ⅰ型时，由图7(a)可以看出：峰值前变形量与峰值后应变量之比 εsa/εsc与应力-应变曲线峰值储存能与峰值后消耗能量之比 φsa/φsc，在其相对关系上可近似地认为是相同的，因此采用φsa/φsc与 εsa/εsc的乘积并不影响Ⅰ型应力-应变曲线岩爆倾向性判别。当应力-应变曲线为Ⅱ型时，应变出现随应力减小而减小的现象(图7(b))，即应变回弹现象，应力峰后能量包括从应力峰值达到应变峰值所消耗的能量 φscf和弹性释放能量 φscr，此时随应变回弹程度的增加，应力峰后岩石破坏释放能量随之增大，计算所得应力峰后消耗的能量 φsc也同时增加，这将造成 φsa/φsc相应减小，若仅以此来判断岩爆倾向性将得到相对偏低的判断；同时考虑到，峰后应变回弹程度与能量释放量呈相同的变化趋势，如图7(b)所示峰后应 变 由 εsc1减 小 到 εsc2，对 应 的 εsa/εsc2将 大 于εsa/εsc1，应力峰值前应变量与应力峰值后总应变量之比 εsa/εsc呈现出随试样破碎时弹性应变储能释放增加而随之增大的变化趋势，因此综合考虑 φsa/φsc与εsa/εsc的共同影响因素，基本可消除针对Ⅱ型应力-应变曲线时单独使用岩爆能量冲击性指标 φsa/φsc，所得岩爆倾向性偏低甚至相反的不足。

综上所述，该判别岩爆倾向性指标的方法，综合考虑了Ⅰ型应力-应变曲线岩石峰前弹性应变储能与峰值后破坏消耗能量的相对关系，同时充分体现出Ⅱ型应力-应变曲线岩石破坏过程弹性储能释放与弹性应变储能积聚的关系，可更为准确地描述岩体岩爆倾向性。

图8 动静组合岩爆倾向性指标DS 与入射能量的关系Fig.8 Relationships between incident and rockburst proneness index under coupled static and dynamic loads DS

针对图6 中以 φsa/φsc计算结果所出现的异常情况，经过增加 εsa/εsc(图7)修正后得到图8 中的动静组合加载岩爆倾向性指标DS结果。图8 中显示DS指标基本消除单独使用 φsa/φsc作为指标所带来的异常结果，并且使岩爆倾向性随加载条件变化而变化趋势更加明显，同时倾向性指标中最大值(44)与最小值(0.79)存在数量级的差别。在较高轴向静载(63，72 MPa)动静组合加载实验时，其岩爆倾向性在较低入射能量冲击作用下具有较高值，随入射能量增加有明显的减小趋势，其减小趋势随轴向静载的增加愈加明显。如轴向静压为72 MPa 时，即抗压强度80%左右，当入射能量从113 J 增大至177 J，其岩爆倾向性指标降低10余倍，从34.5降低至2.7；在轴向静载为63和54 MPa条件时也有相似的变化规律。较低轴向静载(0，18 MPa)动静组合加载实验结果，其岩爆倾向性指标与冲击入射能量变化趋势并不明显，其倾向性指标一直较低，均小于5。由此可见：动静组合加载，由于实验过程中轴向静压和冲击入射能量的不同，根据动静组合实验结果所得岩爆倾向性指标有非常明显的差异，这将有利于较准确的根据岩石实验结果划分岩爆倾向性。

3.2 动静组合加载岩爆倾向性指标建议值

综合考虑动静组合加载条件下砂岩试样岩爆倾向性指标DS与试样破碎能耗密度，结果如图9 所示。并以试样破碎能耗密度的正负值作为辅助评判是否发生岩爆现象，可以将DS=10 作为动静组合加载下岩爆倾向性评价的判据，其评价结果与能耗密度判据结果基本相同。

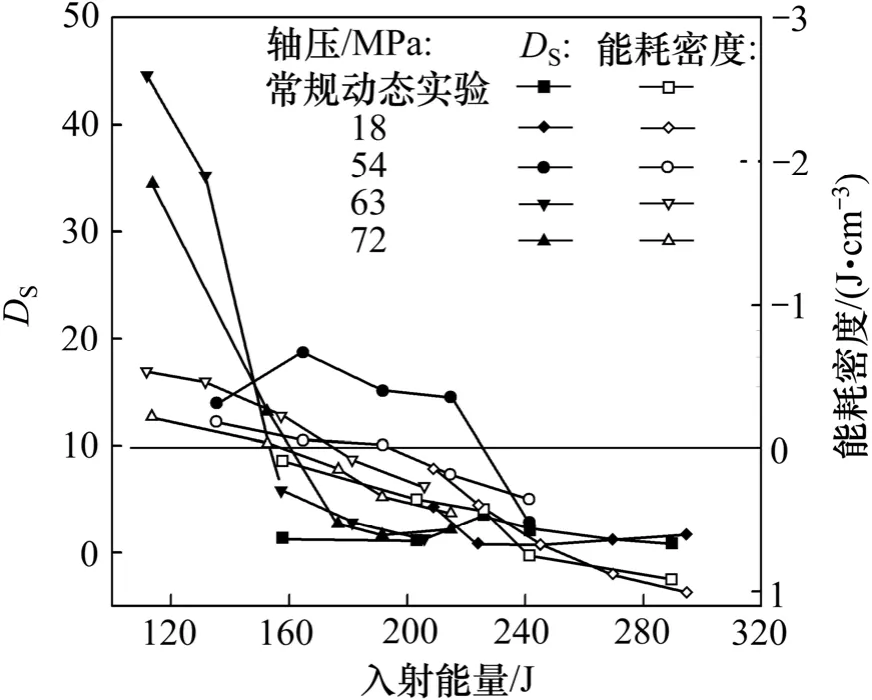
图9 动静组合加载岩爆倾向性指标DS 岩爆判据Fig.9 Criterion for rockburst of proneness index under coupled static and dynamic loads DS

由图9 可见：当轴向轴压63 MPa、冲击入射能量157.40 J 时，岩爆倾向性DS指标计算结果认为无岩爆倾向，但其能耗密度为负值；当轴向轴压54 MPa、冲击入射能量214.55 J 时，岩爆倾向性DS指标计算结果认为有岩爆倾向，但其能耗密度为正值；当轴向轴压54 MPa、冲击入射能量164.62 J 和191.64 J 以及轴向轴压72 MPa、冲击入射能量152.57 J 时，岩爆倾向性DS指标计算结果均认为有明显的岩爆倾向，同时其能耗密度值虽然均为负值但较小。基于以上此类问题，本文建议将DS提高至20，并以此作为判断是否发生明显或不明显岩爆的指标。

结合能量冲击性指标Wcf判据的岩爆判定标准以及本次实验结果，初步建议利用DS指标进行动静组合加载下岩爆倾向性评价的判据：

以此岩爆倾向性指标对动力学实验结果进行分析，可以认为在较低轴向静载的动静组合实验中砂岩不具有岩爆倾向；当轴向静载较高时，砂岩在较低冲击入射能量荷载作用下具有明显岩爆倾向，但随冲击入射荷载能量增加，砂岩试样逐渐转变为无岩爆倾向。

本建议只是根据本次砂岩动静组合实验结果提出，其岩爆倾向性等级划分界限比较粗糙，需进一步实验研究，如进行不同岩性的试验，利用更多的实验结果对其修正，使其岩爆倾向性判据更准确和可靠。

4 结论

1) 动静组合加载条件下，受轴向静载影响，不同冲击能量条件下试样应力-应变曲线峰后特征有明显变化，在较高的轴向静载作用下，随冲击能量的增大，试样动态应力-应变曲线由典型的Ⅰ型曲线逐渐转变为Ⅱ型曲线，同时试样破碎能耗特性由释放能量转变为吸收能量，体现出在较高轴向静载、较小冲击入射能条件是试样的破坏为典型的实验室岩爆现象。

2) 针对动静组合加载实验中的能量转移特点，基于Ⅱ型曲线释放能量原理，提出一种新的动静组合加载实验岩爆倾向性指标，根据新指标中物理量的意义，分析认为新指标能克服现有指标的片面性和差异性，更能反映岩体岩爆倾向性。针对动静组合加载实验结果分析，新指标在一定程度上确实能够较好反映砂岩在动静组合加载条件下的岩爆倾向，并给出岩爆倾向性指标的定量值。

3) 常规动态实验和较低轴向静载的动静组合实验中砂岩不具有岩爆倾向；当轴向静载较高时，砂岩在较低动荷载作用下具有明显岩爆倾向，但随动荷载能量增加，其岩爆倾向快速转变为非岩爆倾向。

4) 动静组合加载岩爆倾向性指标不仅与试样本身特性有关，而且与所承受的静载水平及动载能量密切相关。该指标反映了激励型岩爆的发生受静载和动载两种因素的综合作用的影响，这对激励型岩爆机理的深入研究具有一定参考价值。

[1] 李夕兵, 姚金蕊, 宫凤强. 硬岩金属矿山深部开采中的动力学问题[J]. 中国有色金属学报, 2011, 21(10): 2551-2563.LI Xibing, YAO Jinrui, GONG Fengqiang. Dynamic problems in deep exploitation of hard rock metal mines[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(10): 2551-2563.

[2] 何满潮, 谢和平, 彭苏萍, 等. 深部开采岩体力学研究[J].岩石力学与工程学报, 2005, 24(16): 2803-2813.KE Manchao, XIE Heping, PENG Suping, et al. Study on rock mechanics in deep mining engineering[J] .Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2803-2813.

[3] Singh S P. Technical note: Burst energy release index[J]. Rock Mechanics and Rock Engineering, 1988, 21(2): 149-155.

[4] 蔡美峰, 冀东, 郭奇峰. 基于地应力现场实测与开采扰动能量积聚理论的岩爆预测研究[J]. 岩石力学与工程学报, 2013,32(10): 1973-1980.CAI Meifeng, JI Dong, GUO Qifeng. Study of rockburst prediction based on in-situstress measurement and theory of energy accumulation caused by mining disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10):1973-1980.

[5] 刘立鹏, 汪小刚, 贾志欣. 锦屏二级水电站施工排水洞岩爆机理及特征分析[J]. 中南大学学报: 自然科学版, 2011,42(10): 3150-3156.LIU Lipeng, WANG Xiaogang, JIA Zhixin. Analysis of mechanism and characteristic of rockburst in drainage-hole of Jinping II hydropower station[J]. Journal of Central South University: Science and Technology, 2011, 42(10): 3150-3156.

[6] Kidybinski A. Bursting liability indices of coal[J].International Journal of Rock Mechanics and Mining Sciences,1981, 18(4): 295-304.

[7] 蔡朋, 邬爱清, 汪斌, 等. 一种基于Ⅱ型全过程曲线的岩爆倾向性指标[J]. 岩石力学与工程学报, 2010, 29(A01):3290-3294.CAI Peng, WU Aiqing, WANG bin, et al. A rockburst proneness index based on class Ⅱ whole process curve[J].Chinese Journal of Rock Mechanics and Engineering, 2010,29(A01): 3290-3294.

[8] Saito T. 关于深部隧道工作面岩爆的研究—日本Kan-Etsu隧道实例[C]// 国际岩石力学会议论文选集. 北京: 煤炭工业出版社, 1987: 192-200.Saito T. Study of rockburst of deep working plane: Eexample of Japanese Kan-Etsu tunnel[C]// Proceedings of the International Mechanics and Engineering Conference. Beijing:Coal Industry Press, 1987: 192-200.

[9] 唐礼忠, 潘长良, 王文星. 用于分析岩爆倾向性的剩余能量指数[J]. 中南工业大学学报, 2002, 33(1): 129-132.TANG Lizhong, PAN Changliang, WANG Wenxing. Surplus energy index for analyzing rock burst proneness[J]. Journal of Central South University of Technology, 2002, 33(1):129-132.

[10] 金解放, 李夕兵, 王观石, 等. 循环冲击载荷作用下砂岩破坏模式及其机理[J]. 中南大学学报: 自然科学版, 2012,43(4): 1453-1461.JIN Jiefang, LI Xibing, WANG Guanshi, et al. Failure modes and mechanisms of sandstone under cyclic impact loadings[J].Journal of Central South University: Science and Technology,2012, 43(4): 1453-1461.

[11] LI Xibing, ZHOU Zilong, Lok T S, et al. Innovative testing technique of rock subjected to coupled static and dynamic loads[J]. International Journal of Rock Mechanics and Mining Science, 2000, 37(4): 739-748.

[12] 李夕兵, 周子龙, 叶州元, 等. 岩石动静组合加载力学特性研究[J]. 岩石力学与工程学报, 2008, 27(7): 1387-1395.LI Xibing, ZHOU Zilong, YE Zhouyuan, et al. Study of rock mechanical characteristics under coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering,2008, 27(7): 1387-1395.

[13] 李夕兵, 宫凤强, ZHAO J, 等. 一维动静组合加载下岩石冲击破坏试验研究[J]. 岩石力学与工程学报, 2010, 29(2):251-260.LI Xibing, GONG Fengqiang, ZHAO J, et al. Test study of impact failure of rock subjected to one-dimensional coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 251-260.

[14] 宫凤强, 李夕兵, 刘希灵, 等. 一维动静组合加载下砂岩动力学特性的试验研究[J]. 岩石力学与工程学报, 2010, 29(10):2076-2085.GONG Fengqiang, LI Xibing, LIU Xiling, et al. Experimental study of dynamic characteristics of sandstone under one-dimensional coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10):2076-2085.

[15] YIN Zhiqiang, LI Xibing, JIN Jiefang, et al. Failure characteristics of high stress rock induced by impact disturbance under confining pressure unloading[J].Transactions of Nonferrous Metals Society of China, 2012,22(1): 175-184.

[16] 金解放, 李夕兵, 殷志强, 等. 轴压和围压对循环冲击下砂岩能量耗散的影响[J]. 岩土力学, 2013, 34(11): 3096-3102.JIN Jiefang, LI Xibing, YIN Zhiqiang, et al. Effects of axial compression and confining pressure on energy dissipation of sandstone under cyclic impact loads[J]. Rock and Soil Mechanics, 2013, 34(11): 3096-3102.

[17] 何满潮, 杨国兴, 苗金丽, 等. 岩爆实验碎屑分类及其研究方法[J]. 岩石力学与工程学报, 2009, 28(8): 1521-1529.HE Manchao, YANG Guoxing, MIAO Jinli, et al.Classification and research methods of rockburst experimental fragments[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1521-1529.