基于模糊预测性线性规划的矿山产能分配方案优化分析
2014-04-13陈忠强王李管熊书敏宋明军
陈忠强 ,王李管 ,熊书敏 ,宋明军
(1. 中南大学 资源与安全工程学院,湖南 长沙,410083;2. 中南大学 数字矿山研究中心,湖南 长沙,410083)
对新建矿山而言,其生产规模(即矿石年产量)由矿石储量与设计生产服务年限综合决定,在确定生产规模后,还需要确定矿山产能分配的方案。传统的矿山产能分配方案大多只是以各采区的矿石品位、矿石储量为基础,依靠矿山设计人员或采矿工作者的经验进行确定,缺乏科学系统分析的过程。实际上由于各采区的矿石品位的差异,其单位矿石价格与利润必然不同,而且由于各采区水文地质条件以及与坑口距离等矿石开采条件的差异,生产单位矿石对支护材料、能源以及人力的消费必然也不同。因此需要对矿山产能分配方案进行系统分析,才能达到资源能源与人力的最优配置与矿山企业利润的最大化。传统的对于此类资源优化配置问题大多采用线性规划模型进行求解计算加以确定,然而对于矿山产能分配方案的优化配置而言,一般的线性规划问题显然无法解决。首先,对于新建矿山而言,各采区生产单位矿石的资源、能源以及人力等的消耗并不是一个确定值,只能根据条件相似矿山而确定一个大概范围;其次在矿山的生产实践中,对于各类投资往往并不是完全确定的,在矿山建设过程中都存在追加或者减少资源、能源以及人力投入的可能性,这些投入都只是一个模糊的概念。而一般线性规划模型只能求解目标与约束都是确定值的问题,对于此类问题显然无法解决。针对此种情况,在一般线性规划问题中引入模糊数学[1]与灰色理论[2]的思想。对于各采区生产单位矿石产品所需要消耗的资源、能源以及人力等属于某一范围的值,采用灰数[3-5]表示。而对于资源、能源以及人力总投入等常常有追加或减少的情况,采用模糊约束,这样就建立了矿山产能优化分配的模糊预测性线性规划模型,对模型中属于某一范围的值利用多种灰色预测理论进行精度比较后[6-7]进行预测,使之白化变为定值,简化为模糊线性规划[8-10],对模糊线性规划通过构建隶属函数,并利用模糊最优判决条件转变为一般线性规划问题,进而进行求解得到矿山的最优产能分配方案。模糊预测性线性规划模型综合了模糊线性规划与灰色预测性线性规划[11-12]的特征,并且可以在一定条件下转化为模糊线性规划与灰色预测性线性规划,很适合解决目标与参数皆不明确时的产能优化分配问题。因此相对于传统的几类线性规划模型,在生产实践中有着更大适用空间与应用价值。
1 模型建立
1.1 模糊预测性线性规划理论
对于矿山产能分配问题,如果其目标与约束都明确,则其为确定性的一般线性规划问题,其标准形式为:

式中:C 为价格向量,A 为消耗矩阵,b 为约束向量,X 为决策向量。
当矿山的资源、能源与人力等约束条件及目标函数模糊,而且生产单位矿石的各种资源、能源及人力消耗以及所获得的利润都不确定,只能确定大概范围,即为有界灰元,此时线性规划模型变为:

上述模型由于兼有模糊数学与灰色理论的思想,被称为模糊预测性线性规划模型[13-17],该模型实际上是模糊线性规划与灰色预测性线性规划的综合,在有界灰元被白化的情况下可转化为模糊线性规划问题,在模糊关系明确的情况下可转化为灰色预测性线性规划问题。
对模糊预测性线性规划的一般求解思路为,将各灰元进行白化,变为模糊线性规划问题,然后按照模糊线性规划问题的解法进行求解。
1.2 系统建模
1.2.1 模糊预测性线性规划模型构建
设一矿山有n 个不同的采区,每个采区的产能分别为x1,x2,…,xn,则其矿山产能分配决策向量为:

由于各采区矿石地质品位及开采条件的差异,各采区生产的单位矿石其利润c1,c2,…,cn并不一样,而且单位矿石的利润每一年都随着价格,原材料、人力的变化而变化,即单位矿石的利润是灰色的,则利润向量C 可变为灰色利润向量C(⊗):

i 矿区生产单位矿石所消耗的j 种物质(材料、能源或人力等)aij也不是一个定值,随着技术革新与科技进步,生产单位矿石所消耗的材料必然会逐年发生变化,因此aij也是一个灰色的数,即aij(⊗),据此得到消耗矩阵A(⊗)为:

而外部环境为矿山生产所提供的资源、能源以及人力等投入,也并不是完全一成不变的,往往会随着投资方对形势的判断,决策者的意图以及外部环境的变化而有追加或减少投入的情况,即投入约束向量B为模糊向量,据此建立起矿山产能配置的模糊预测型线性规划模型如下:

1.2.2 灰元系数白化
对生产单位矿石的利润与消耗这些有界灰元,模糊预测性线性规划模型借鉴灰色预测型线性规划模型采用利润定位系数ρj以及消耗定位系数δij对灰元系数进行白化,白化处理方式如下:
利用利润定位系数ρi对i 采区生产单位矿石获得的利润进行白化:
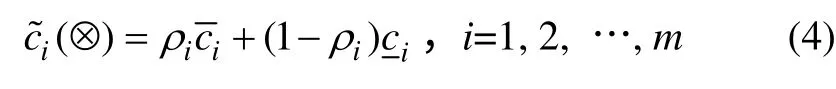
利用消耗定位系数δij对i 采区生产单位矿石所消耗的第j 种资源或能源进行白化:

利润定位系数及消耗定位系数的准确确定关系到未来矿山产能分配的合理性与可靠性。对此,采用多种预测模型进行精度比较后,选择最优预测模型来确定利润定位系数与消耗定位系数,常用的灰色预测模型有GM(1,1)模型、微分verhulst模型以及差分verhulst模型。
对3 种模型进行精度比较[18],选取精度最高的模型进行各定位系数的预测。
1.2.3 模糊线性规划模型求解
将各系数准确白化后,矿山陈能配置的模糊预测性线性规划模型就变为了模糊线性规划模型:

将模糊目标与模糊约束结合,得到如下形式:

即

确定模糊目标及模糊约束的隶属函数,由于隶属函数一般都要满足严格递减的要求,因此其确定原则一般如下:
当(A′ X )i≤ bi时, μi( x) = 1;
当bi<(A′ X )i≤bi+di时,0<μi( x) <1
当(A′ X)i> bi+di时, μi( x) =0
i=1, 2, …, m,[bi,bi+di]称为违反区间。
根据上述原则,且为计算方便考虑,因此隶属函数取为一条斜率为负的直线,为
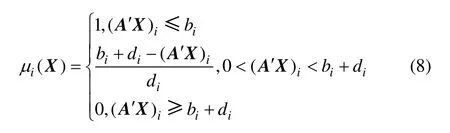
根据模糊数学基本理论,最优判决条件为
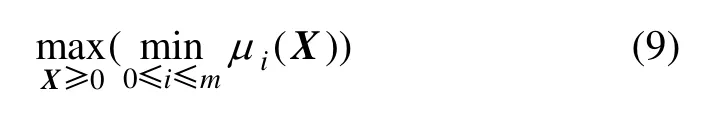
根据最优判决条件即可将模糊线性规划转变为一般的线性规划模型进行求解,为求解方便,令

得到以求最大隶属度λ 为目标函数的一般线性规划模型,模型形式如下:

对上述线性规划模型求解,即可得到模型的最优解,从而得到矿山产能分配的模糊预测性线性规划模型的最优解,利用最优解的结果即可对矿山产能进行优化配置。
矿山产能配置方案的模糊预测性线性规划模型的建模及求解过程见图1。

图1 矿山产能分配求解流程Fig.1 Solving process of mining production allocation
2 实例分析
2.1 矿山简况
湖北某2013 年拟建磷矿山矿区面积6.97 km2,设计生产规模为年产原矿90 万t,由于矿区存在一条南北走向的大型逆断层,上下垂直高差足有近百米,天然地将矿区分为东西两大采区,其中东采区设计利用的资源储量为730 万t,西采区设计利用的资源储量为1 480 万t,在对矿山产能方案进行分配时,初始设计为按照各采区的资源储量比例进行分配,即东采区设计开采规模为30 万t/a,西采区设计开采规模为60 万t/a。但是由于开采条件及东西采区矿石品位的差异,东采区单位矿石的利润要大于西采区,因此仅仅按照各采区资源储量的比例进行产能分配,显然不是最优方案,不能使得利润最大。但是如果利润最大化,就要使单位矿石利润较大的东采区的生产规模尽量大,但是由于水文工程及开采条件的限制,东采区生产单位矿石所需要的木材,人力以及电力需求都较大,但是这些恰恰是该新建矿山目前生产的紧缺资源或能源,因此需要综合考虑产品利润及外部环境的约束,来确定矿山最优的各采区产能分配方案。
该矿山由于是新建矿山,外部环境并不十分完善,而且由于周围磷矿山较多,因此技术工人相对不足,电力供给以及支护材料都很紧张,人力、电力以及部分支护用材料(主要是木材)成为矿山生产规模的主要制约因素,统计相似矿山的生产实际资并分析估计,得到东采区每生产1 t 矿石的消耗为:工时1.87~3.62个,电力12~30 kW·h,木材0.000 36~0.000 63 m3;西采区每生产1 t 矿石的消耗为:工时1.45~2.87 个,电力10~24 kW·h,木材0.000 26~0.000 47 m3。以当前的市场价格进行测算,东采区生产单位矿石的利润约为180 元/t,西采区生产单位矿石的利润约为130 元/t。而矿山目前已经确定招募的一线技术工人为850 人(折算为2 040 000 个工时),每年得到的外部电力供给约为1 800 万kW·h,每年当地采伐得到的木材约为510 m3。根据矿山计划,将继续招募工人,并在外部建设1 个小型的变电站,因此预计一线技术工人将有可能达到900 人左右,每年得到的外部电力供给有可能达到2 000 万kW·h,而木材也有可能达到550 m3。据此,得到该矿山产能分配优化的灰色预测型线性规划模型如下:

其中:东采区的矿石产量为x1,西采区的矿石产量为x2。灰参数 a11( ⊗) ∈[1.87,3.62], a12(⊗ ) ∈[1.47,2.87],a21( ⊗) ∈[12,30],a22( ⊗) ∈[10,24],a31( ⊗)∈[0.000 36,0.000 63], a32( ⊗) ∈[0.000 26,0.000 47]。
若想对矿山产能分配的模糊预测性线性规划模型进行求解,首先要利用各定位系数对灰参数进行白化,去掉其灰色属性,将其转变为一般的模糊线性规划问题。
2.2 多预测模型的定位系数白化
根据相关统计资料,采用式(7)进行反算得到类似东采区的矿山与类似西采区的矿山2004~2012 年的消耗定位系数见表1。
为得到与实际情况相符的产能分配结果,各消耗系数的准确预测白化是关键,以往的灰色预测型线性规划模型在对各类定位进行白化时,大多是以GM(1,1) 模型进行白化的,实际上对于各类定位系数而言,GM(1,1)模型并不一定是预测精度最高的模型,因此需要采用多种预测模型进行预测精度比较后,再选择精度最高的模型进行定位系数的预测白化。

东采区矿石生产消耗定位系数 西采区矿石系生数产消耗定位年份 工时消耗系数δ11电力消耗系数δ21木材消耗系数δ31工时消耗系数δ12电力消耗系数δ22木材消耗系数δ32 2004 0.89 0.88 0.90 0.71 0.87 0.84 2005 0.86 0.84 0.85 0.66 0.82 0.80 2006 0.81 0.79 0.81 0.61 0.78 0.76 2007 0.76 0.76 0.75 0.55 0.75 0.73 2008 0.72 0.72 0.70 0.51 0.72 0.70 2009 0.69 0.69 0.66 0.46 0.69 0.64 2010 0.67 0.65 0.61 0.43 0.67 0.59 2011 0.64 0.62 0.58 0.39 0.65 0.54 2012 0.62 0.61 0.55 0.36 0.64 0.50
以东采区单位矿石生产的工时消耗定位系数的预测白化为例,东采区矿石生产的工时消耗定位系数的原始序列为


得到GM(1,1)模型的时间响应序列为:

微分verhulst 模型的时间响应序列为:

差分verhulst 模型的时间响应序列为:

其中:k=0, 1, 2, …, n。

预测值实际值GM(1,1)模型微分VERHULST模型差分VERHULST模型0.89 0.89 0.89 0.89 0.86 0.85 0.85 0.85 0.81 0.81 0.81 0.81 0.76 0.77 0.77 0.77 0.72 0.73 0.73 0.73 0.69 0.70 0.70 0.70 0.67 0.67 0.67 0.67 0.64 0.64 0.64 0.64 0.62 0.61 0.62 0.62残差平方和 0.000 5 0.000 4 0.000 4相对精度/% 99.42 99.56 99.56小误差概率p/%100 100 100后验比值c 0.081 1 0.070 2 0.070 2
根据误差分析结果,微分verhulst 模型与差分verhulst 模型相对于GM(1,1)模型的预测精度要高,而微分verhulst 模型与差分verhulst 模型的精度是一样的,因此可任意采用两模型中的任意一种模型对2013年的东采区工时消耗系数进行预测,得到两模型的预测结果是一致的,均为0.59。
按照以上思路对各定位系数进行预测,得到最优的预测模型及相应的预测结果见表3。

东采区矿石生产消耗定位系数 西采区矿石生产消耗定位系数工时消耗系数δ11 电力消耗系数δ21 木材消耗系数δ31 工时消耗系数δ12 电力消耗系数δ22 木材消耗系数δ32最优模型 微分verhulst差分verhulst 微分verhulst 微分verhulst 微分verhulst 微差分分vv ee rr hh uu ll ss t t 差分verhulst预测结果 0.59 0.59 0.51 0.33 0.63 0.45
2.3 模糊线性规划模型求解
根据表3 的定位系数预测结果,确定该矿山的吨矿产能分配东采区生产1 t 矿石的消耗为:工时消耗a11=2.90 个,电力消耗a21=22.62 kW·h,木材消耗a31=0.000 50 m3;西采区生产1 t 矿石的消耗为工时消耗a11=1.92 个,电力消耗a21=18.82 kW·h,木材消耗a31=0.000 36 m3。根据单位矿石的消耗将该矿山的产能分配模糊预测型线性优化模型转化为模糊线性规划模型:

根据模糊线性规划相关定义,得到工时供给的违反区间为[2 040 000,2 160 000],电力供给的违反区间为[18 000 000,20 000 000],坑木供给的违反区间为[510,550]。
在不考虑追加投入的情况下,对模糊预测线性规划模型进行求解,即对线性规划模型

求解得到当x1=343 820 t,x2=543 180 t,得到最大利润S=132 500 000 元。
将最大可能的追加投入全部加入到约束条件后再进行求解,即线性模型变为

求解得到当 x1*=440 820 t, x*2=459 180 t,得到最大利润S*=139 040 000 元。
据此构建出目标函数以及模糊约束条件的隶属函数如下。
目标函数隶属函数为

工时约束隶属函数 μ1( X )为

电力约束隶属函数 μ2( X )为

木材约束隶属函数 μ3( X )为

根据最优判决条件,令

得到以求最大隶属度λ 为目标函数的一般线性规划模型,模型形式如下:

得到最优解λ=0.359 1,x1=423 580,x2=453 130,年最大利润为135 151 300 元。
2.4 产能结果分析
根据取得最大利润时λ=0.359 1,得到此时一线人工人数为882 人,电力年供应量为19 281 800 kW·h,木材年供应量为536 m3。即在上述条件下,可以得到矿山产能分配的最优结果,此时东采区年产矿石量为42.36 万t,西采区年产矿石量为45.31 万t,最大年利润为1.35 亿元,此时矿山年总产量为87.67 万t。
按照产能优化分配结果,东采区可以生产17 a,西采区可以生产32 a。
3 结论
1) 在一般线性规划模型的基础上,综合模糊数学与灰色系统理论思想,建立模糊预测型线性规划模型,利用模糊数学的思想对约束条件进行了模糊处理,灰色理论的思想对各类消耗进行了有界灰元处理。经实例检验,该模型对于矿山产能分配时有追加投入以及各种消耗系数多随时间在一定范围内变动的情况非常适用。模型求解思路清晰,求解结果准确,可在相似领域进行推广使用。
2) 在对模糊预测型线性规划模型的各类有界灰元进行白化时,对灰色系数的白化一定要准确,这关系到模型最终求解结果的可靠性。采用多种预测模型进行精度比较后再进行白化的方法得到的结果比单一预测模型直接白化预测的结果要更科学、准确。
3) 隶属函数的构建采用的是直线型隶属函数,在很多情况下,其隶属函数并不一定是直线型,因此在构造隶属函数时,除了考虑求解的简便性外,还应根据实际情况灵活选取隶属函数类型,这样才能保证求解过程更加科学,求解结果更加可靠。
[1] 高淑萍, 刘三阳. 一类模糊线性规划的求解方法及应用[J].系统工程与电子技术, 2005, 27(8): 1412-1415.GAO Shuping, LIU SANyang. Solution to fuzzy linear programming and its application[J]. Systems Engineering and Electronics, 2005, 27(8): 1412-1415.
[2] 邓聚龙. 灰色系统基本方法[M]. 2 版. 武汉: 华中科技大学出版社, 2005.DENG Julong. Basic method of grey system[M]. 2nd ed. Wuhan:Huazhong University of Science and Technology Publishing House, 2005.
[3] 王浙明, 史惠祥, 苏雨生, 等. 灰色关联模型用于工程方案优化[J]. 中国给水排水, 2002, 18(1): 81-87.WANG Zeming, SHI Huixiang, SU Yusheng, et al. Grey relational model used in engineering scheme optimization[J].China Water & Waste Water, 2002, 18(1): 81-87.
[4] 伍爱友, 肖红飞, 王从陆, 等. 煤与瓦斯突出控制因素加权灰色关联模型的建立与应用[J]. 煤炭学报, 2005, 30(1) : 58-61.WU Aiyou, XIAO Hongfei, WANG Conglu, et al. Establishment and application of weights and gray association model based on coal and gas outburst controlled factors assessment[J]. Journal of China Coal Society, 2005, 30(1): 58-61.
[5] GU Hui, SONG Bifeng. Study on effectiveness evaluation of weapon systems based on grey relational analysis and TOPSIS[J].Journal of Systems Engineering and Electronics, 2009, 20(1):106-111.
[6] XIE Naiming, LIU Sifeng. Research on evaluations of several grey relational models adapt to grey relational axioms[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 304-309.
[7] 郑海力, 陈建宏, 胡达涛. 矿山企业经济的多层次嵌套型灰色关联分析[J]. 湖南科技大学学报(自然科学版), 2009(4):85-90.ZHENG Haili, CHEN Jianhong, HU Datao. Multi-layer nested grey incidence analysis to economic of mining enterprise[J].Journal of Hunan University of Science & Technology (Natural Science Edition), 2009(4): 85-90.
[8] 谢小良, 符卓. 模糊机会约束规划下的物流配送路径优化[J].计算机工程与应用, 2009, 45(18): 215-218.XIE Xiaoliang, FU Zhuo. Optimization of logistics delivery routing problem by using fuzzy chance constrained programming[J]. Computer Engineering and Applications, 2009,45(18): 215-218.
[9] 张成, 杨万才. 模糊规划的对偶理论[J]. 辽宁师范大学学报(自然科学版), 2005, 28(1): 1-6.ZHANG Cheng, YANG Wancai. Duality theory of fuzzy programming[J]. Journal of Liaoning Normal University(Natural Science Edition), 2005, 28(1): 1-6.
[10] 张会娟, 张强. 基于模糊机会约束规划的最优产量决策[J].运筹与管理, 2009, 18(6): 89-96.ZHANG Huijuan, ZHANG Qiang. The optimun output quantity decision based on fuzzy chance constrained programming[J].perations Research And Management Science, 2009, 18(6):89-96.
[11] 林奇宁, 吴德雄, 杨智雄. 矿区煤炭开发的灰色规划探讨[J].山东科技大学学报(自然科学版), 2001, 30(1): 45-47.LIN Qining, WU Dexiong, YANG Zhixiong. A discussion on grey planning of coal exploitation in mining area[J]. Journal of Shandong University of Science and Technology (Natural Science), 2001, 30(1): 45-47.
[12] 张国新, 阳静, 包强. 基于灰色规划的军队装备科研项目鉴定评价[J]. 运筹与管理, 2006, 15(1): 116-120.ZHANG Guoxin, YANG Jing, BAO Qiang. Evaluation of appraisal of military equipment scientific research project based on grey program[J]. Operations Research and Management Science, 2006, 15(1): 116-120.
[13] 张云龙, 刘茂. 灰色GM(1,1)模型在火灾事故预测中的应用[J]. 南开大学学报(自然科学版), 2009, 42(1): 11-15.ZHANG Yunlong, LIU Mao. Application of grey prediction model GM(1,1) in fire accident[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis, 2009, 42(1): 11-15.
[14] 郭丽萍, 孙伟, 郑克仁, 等. 非等时距GM(1,1)直接模型及其在材料试验数据处理中的应用[J]. 东南大学学报(自然科学版), 2004, 34(6): 39-41.GUO Liping, SUN Wei, ZHENG Keren, et al. Non-equal interval GM(1,1) direct model and its application in processing of materials experimental data[J]. Journal of Southeast University (Natural Science Edition), 2004, 34(6): 39-41.
[15] 肖有才, 张秀成, 王宏艳. 灰色理论在预测深埋型矿井涌水量中的应用[J]. 辽宁工程技术大学学报, 2004, 23(2): 175-177.XIAO Youcai, ZHANG Xiucheng, WANG Hongyan.Application of grey theory model in prediction of pit water discharge in coal mine[J]. Journal of Liaoning Technical University, 2004, 23(2): 175-177.
[16] 李建刚, 白润才, 刘光伟, 等. 露天矿行车事故频次的灰色预测[J]. 辽宁工程技术大学学报, 2005, 24: 6-8.LI Jiangang, BAI Runcai, LIU Guangwei, et al. Grey forecast of travel accident frequency in open-pit mine[J]. Journal of Liaoning Technical University, 2005, 24: 6-8.
[17] 郭宏斌, 陈建宏, 杨珊, 等. 基于模糊预测性线性规划与改进灰色聚类分析的烟草企业最优生产方案选择方法[J]. 科技导报, 2012, 30(26): 48-55.GUO Hongbin, CHEN Jianhong, YANG Shan, et al. The selection method for tobacco company best production plan based on fuzzy predictability linear programming model and improved gray cluster analysis theory[J]. Science and Technology Review, 2012, 30(26): 48-55.
[18] 罗云, 吕海燕, 白福利. 事故分析预测与事故管理[M]. 北京:化学工业出版社, 2005.LUO Yun, LÜ Haiyan, BAI Fuli. Accidents and accident analysis and prediction[M]. Beijing: Chemical Industry Press, 2005.
