一类高阶非线性系统的鲁棒反推终端滑模控制
2014-04-13苏磊姚宏杜军冀捐灶
苏磊,姚宏,杜军,冀捐灶
(1. 空军工程大学航空航天工程学院,陕西 西安,710038;2. 空军工程大学理学院,陕西 西安,710051)
滑模控制(SMC)是现代控制理论中的重要方法,具有对系统匹配不确定性的完全鲁棒性,但是难以处理系统非匹配不确定性[1-3]。反推控制(BC)能够有效处理系统中的非匹配不确定性[4-5]。将BC 和SMC 相结合,设计反推滑模控制器,可以实现对同时含有匹配和非匹配不确定性系统的鲁棒控制[6-8]。在反推滑模控制方法中,存在有3 个主要问题:
1) 在逐步递推中,需要对虚拟控制函数反复求导,从而产生“微分爆炸”现象[9-10]。基于文献[10]提出的动态面控制 (DSC)方法,文献[11]在设计反推滑模控制器时,通过引入一系列低通滤波器(LPF),实现对虚拟控制律的滤波估计,较好的解决了这一问题。
2) 传统SMC 中,采用由符号函数构成的切换函数,控制信号在不同控制器之间频繁切换,造成控制输入的不连续性,即产生抖振现象[6,12]。采用饱和函数或者双曲正切函数,可有效降低控制抖振。如文献[13]在终端滑模(TSM)控制器中采用饱和函数,但是系统只能收敛到滑模面的一个边界层处,控制性能降低;文献[7]在SMC 中采用双曲正切函数,但是未同时考虑控制对象中参数摄动和外界扰动的影响。
3) 传统SMC 中,抖振意味着系统对不确定性的鲁棒性,两者密切相关,以降低系统鲁棒性为代价消除系统抖振是毫无意义的。
恢复和增强无抖振滑模鲁棒性的一种重要方法是采用不确定性估计策略[14-15]。非线性干扰观测器(NDO)[16-17]根据已知系统信息,通过对系统不确定性和外界干扰的实时观测进行反馈补偿,具有目标明确、物理含义清晰且系统结构和被控系统相互独立等特点。文献[18-19]分别在反推滑模和动态TSM 中采用NDO 对系统不确定性和外界干扰进行观测补偿,并用于飞行器控制,取得了较好的控制效果。针对一类同时具有建模误差和非匹配外界干扰的高阶非线性系统输出跟踪问题,本文作者设计了一种基于NDO 的鲁棒自适应反推TSM 控制方案。在控制方案中,针对由外界未知干扰引起的系统非匹配不确定性,设计NDO 进行观测补偿;借鉴DSC 方法简化反推过程控制器设计;引入边界层厚度设计系统建模误差自适应律,并采用双曲正切函数替换传统SMC 中的符号函数,提高控制信号平滑性;给出NDO 和受控系统的稳定性定理及证明,指出观测误差和跟踪误差一致终结有界,并通过仿真对比进行验证。本文提出的控制方案,在实现对指定轨迹精确跟踪的同时,能够有效消除控制信号抖振,且具有较好的鲁棒性。
1 问题描述
本文的研究对象为一类同时具有非匹配不确定性和建模误差的n 阶非线性不确定系统:
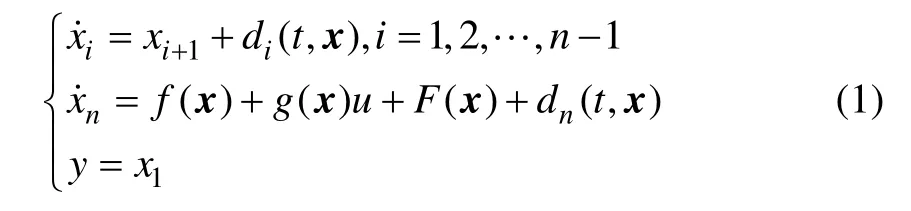
其中:x=[ x1, x2,… , xn]T∈Rn为系统状态;u ∈R1和y ∈R1分别为系统输入和输出;f = f( x )为已知光滑非线性状态函数;g = g( x )为控制增益函数,并有g-1存在,且f 和g 满足Lipschitz 条件;F =F( x)=Δf( x)+Δg ( x )u为系统建模误差函数,其中 Δf ( x )为状态建模误差函数, Δg ( x )为控制增益不确定函数;di=di( t, x ),i=1, 2, …, n 为由外界干扰引起的系统非匹配不确定性。令系统轨迹指令为 xd,对式(1)及 xd进行以下假设。
假设1:di, i=1, 2, …, n 上界未知,但满足Lipschitz连续有界和一阶导数有界,即
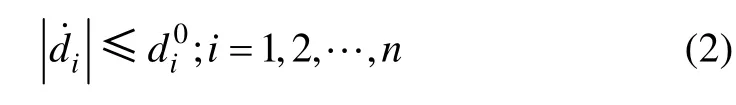
其中: di0∈R+已知。
假设2:F 连续可导,且有F˙ ≈0。
假设3: xd有界且满足一阶可导。
本文控制器设计的任务是针对如式(1)所示的一类高阶非匹配不确定非线性系统,在假设1~3 下,考虑F 和di, i=1, 2, …, n 影响,设计轨迹跟踪控制器,使得系统输出y 稳定跟踪指定的参考轨迹 xd,并在消除控制抖振的同时,增强系统的鲁棒性。
2 基于NDO的反推TSM控制器设计
本文设计的基于NDO 的反推TSM 控制方案如图1 所示。
控制器设计中,首先针对di, i=1, 2, …, n 设计NDO 进行观测补偿,确保系统对不确定性的鲁棒性;其次将BC 和TSM 相结合,并基于DSC 方法,在BC中引入LPF 解决“微分爆炸”问题;在BC 最后一步设计建模误差自适应律和终端滑模控制律,最终实现系统输出对指定轨迹的稳定跟踪。

图1 基于NDO 的反推TSM 控制方案Fig.1 NDO based backstepping TSM control method
2.1 NDO 设计及收敛性分析
第Ⅰ类NDO:当i=1, …, n-1 时,针对di设计NDO 进行观测补偿。
定理1:如果设计系统第i,i=1, …, n-1 阶的NDO状态方程为[16]


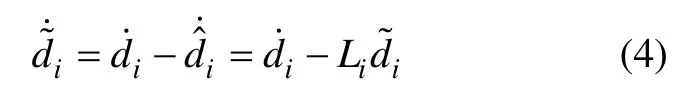
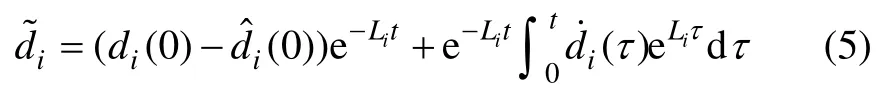




第Ⅱ类NDO:当i=n 时,针对dn设计NDO 进行观测补偿,此时dn和系统第n 阶中的不确定性F =F ( t, x )相互耦合。
定理2:如果设计系统第n 阶NDO 状态方程为

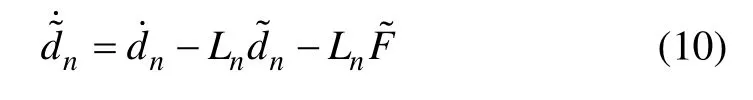

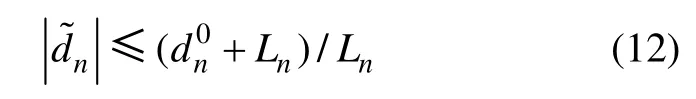

2.2 反推TSM 控制器设计及稳定性分析
控制器设计中,定义式(1)状态跟踪误差为

其中:αi-1为第i 步的虚拟控制函数。
反推TSM 控制器由BC 和TSM 相结合设计而成,共有n 步,前n-1 步采用BC 设计过渡控制函数;第n 步设计系统建模误差自适应律和TSM 控制器。具体设计过程详述如下。
步骤1:由式(1)和式(13),对z1求导可得
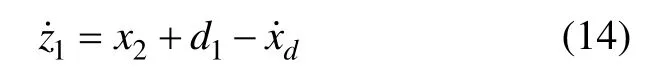
式(14)中,定义x2为
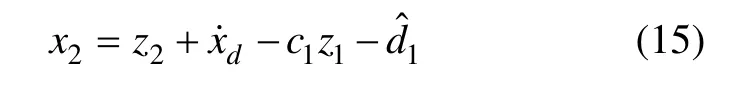
其中: c1∈R+为待定常数。由式(14)~(15)可得
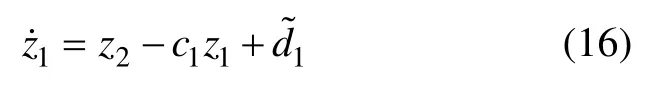
基于式(16),取步骤1 的过渡控制函数 β1如下:

步骤i(i=2, 3, …, n-2):由式(1)和式(13)有

式(18)中,定义xi+1为
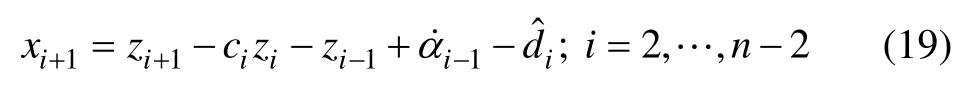
其中:ci∈R+, i=2, …,n -2为待定常数。由式(18)~(19)可得:

基于式(20),取步骤i 的过渡控制函数 βi为

步骤n-1:由式(1)和式(13)有

此时,不同于步骤i,i=2, 3, …, n-2,定义xn为

其中:cn-1∈R+为待定常数。由式(22)~(23)可得

基于式(24),取步骤n-1 的过渡控制函数βn-1为

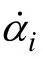

其中:τi∈(0,1)为LPF 时间常数。定义LPF 边界误差为 ωi= αi- βi,由式(26)可得

对 ωi求导,由式(27)可得

为便于系统控制器设计,在此给出引理1。
引理1:对于∀x,y ∈Rn,有如下不等式成立:


由引理1 和式(28)可得:
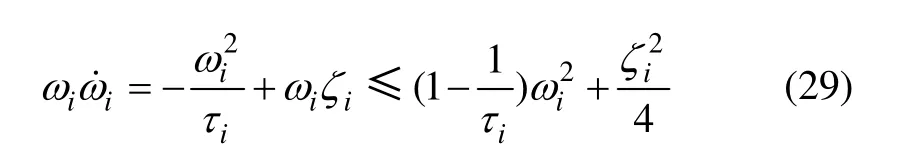
定义步骤i(i=1, …, n-1)的Lyapunov 函数为
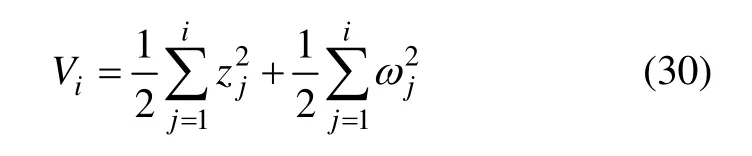
由式(16),(20),(24)和(30)可得,当i=1, …, n-2时,有

当i=n-1 时,有

ξ 为正常数,定义如下:

步骤n:由式(1)和式(13)有

设计如下的系统终端滑模面:

其中:μ 为待定参数;p 和q 为正奇数,满足1<p/q<2。
则对于本文设计的基于NDO 的反推TSM 轨迹跟踪控制方法,其稳定性如定理3 所述。
定理3:针对如式(1)所示的一类高阶不确定非线性系统输出跟踪问题,当系统不确定性和跟踪轨迹满足假设1~假设3 时,如果设计如式(3)和式(9)所示的NDO,设计系统建模误差自适应律为

设计系统终端滑模控制律为
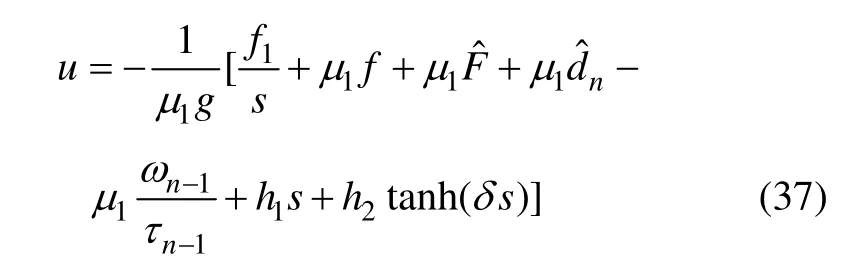


则系统是Lyapunov 稳定的,且输出跟踪误差一致终结有界。其中μ ,p,q,h1,h2,τi, ci,和Li(i=1, 2, …,n)是合适的设计参数。
证 明: 式(37) 中, tanh(δ s) =(eδs-e-δs)/(eδs+e-δs)为连续可导的双曲正切函数,用来替换传统滑模中不连续不可导的符号函数sgn( s ),当调节系数δ →∞有tanh(δ s) →sgn( s)。对式(35)中s 求导并代入 μ1得

定义步骤n 的Lyapunov 函数为
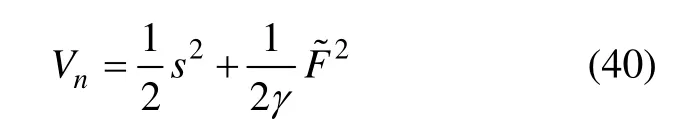
对式(40)求导可得

定义系统Lyapunov 函数为V = Vn+Vn-1,即
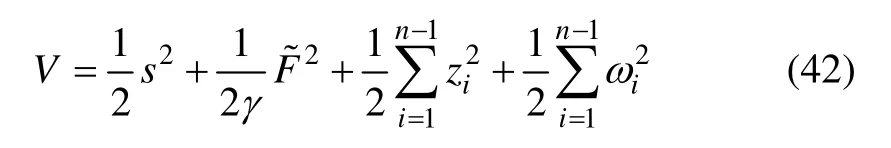
对V 求导,并由假设2 可得

把式(38)代入式(43)可得
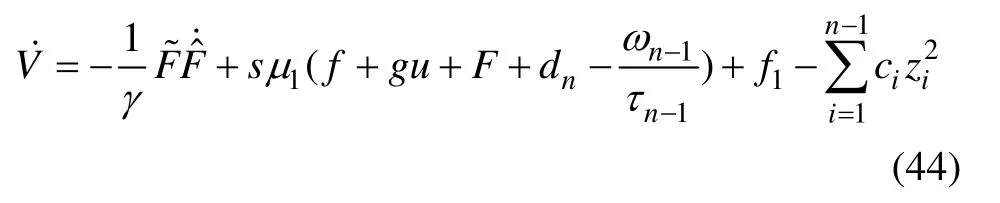
把式(36)~(37)代入式(44)可得



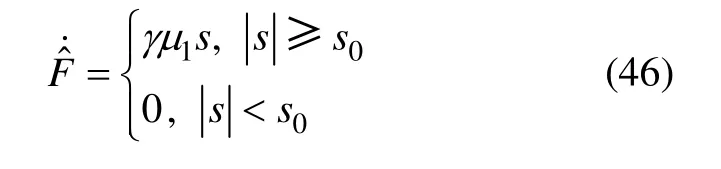
3 数值仿真及分析
考虑如式(47)所示三阶不确定非线性系统:

即由外界未知干扰引起的系统不确定性为 d1=1.5sint ,d2=x1sin( x3) -0.8t e-0.5t, d3=0.1cos(2t )+0.6x2x3sinx1。系统状态函数f=2x13+x1sin x2+3x1x2x3,控制增益g = 3 +0.5sinx1,系统建模误差F=0.02x22+0.01sinx2+0.01x2x3。
设系统跟踪轨迹xd=sin( t) +sin(0.5t ),初始状态x0=[0.1,0.2, -0.2]T。控制器参数取值如下:h1=2,h2=10, c1=5, c2=20, L1=15, L2=10, L3=50, μ=1.5, γ=0.01,s0=0.01, p=7, q=5, δ=2, τ1=0.15, τ2=0.05。
首先,采用本文设计的基于NDO 的反推TSM 控制器,称为控制器1;其次,设计无NDO 的传统终端滑模控制器,且采用饱和函数sat( s )替换符号函数,取饱和函数边界层厚度φ =0.05,称为控制器2。在相同控制参数和不确定性下,对式(47)进行轨迹跟踪仿真。控制器1 和控制器2 的跟踪轨迹、跟踪误差和控制输入分别设为y1,e1,u1和y2,e2,u2。仿真结果如图2~6 所示。
由图2 和图3 可知:在控制器1 和控制器2 作用下,系统(47)输出均能够实现对xd的稳定跟踪,y1和xd基本重合,y2和xd则有较大误差,即跟踪误差e1明显小于e2,同时,跟踪误差有限时间内收敛到零点的一个有限邻域内。
由图4 和图5 可知:对于2 个控制器的控制信号而言,u1平滑无抖振,而u2在开始出现剧烈抖振,经过约2.1 s 才进入无抖振状态,且控制信号幅值大于u1。

图2 2 种控制器的跟踪轨迹Fig.2 Tracking trajectories of two controllers
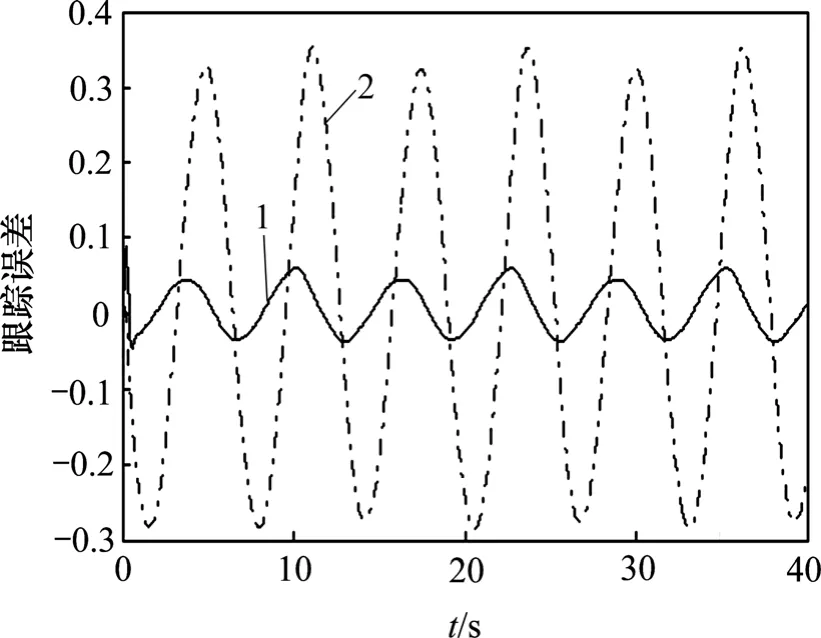
图3 2 种控制器的跟踪误差Fig.3 Tracking errors of two controllers

图4 控制器1 的控制输入和自适应律Fig.4 Control input and adaptive law of controller 1
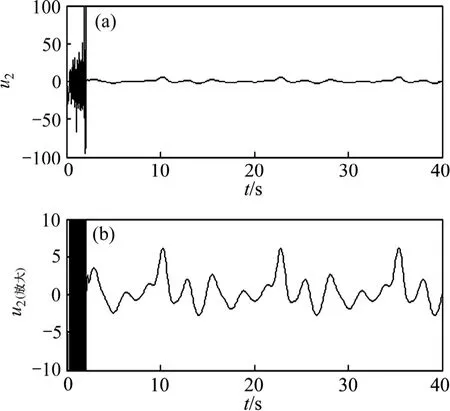
图5 控制器2 的控制输入Fig.5 Control input of controller 2
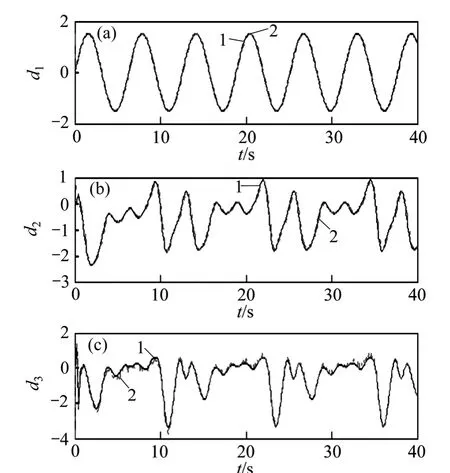
图6 系统不确定性和NDOs 观测值Fig.6 System uncertainties and observations of NDOs
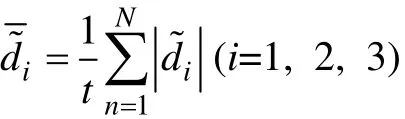
进一步,定义2 种控制器的跟踪误差e 和控制能耗E 如下:

则可得2 种控制器的性能比较如表1 所示。

控制器类型e E控制器1 0.029 114.294控制器2 0.223 431.403
由表1 可知:与控制器2 相比,本文设计的控制器1 具有跟踪误差小和控制能耗低的优点,同时也验证了饱和函数虽然能够降低抖振,却是以降低跟踪精度和提高控制能耗为代价的;不足之处在于:由于NDO 观测误差的存在和自适应律调整能力的有限,导致系统输出跟踪存在一定的误差,但是可以通过控制参数的调整,把输出跟踪误差限制在精度要求之内。
4 结论
1) 针对一类高阶非匹配不确定非线性系统,结合动态面控制思想,设计了一种基于NDO 的反推TSM控制方法。设计NDO 实现对由外界干扰引起的系统非匹配不确定性的精确观测和补偿,NDO 指数收敛且观测误差有界;引入自适应律边界层厚度设计鲁棒自适应律,实现对系统建模误差的估计;借鉴动态面控制方法解决“微分爆炸”问题,最终实现系统输出对指定轨迹的稳定跟踪,且跟踪误差一致终结有界。
2) 与无NDO 的传统终端滑模控制器相比,本文设计的控制方法跟踪精度高,控制能耗低,并在消除抖振的同时,确保了控制器的鲁棒性。
[1] Young K D, Utkin V I, Ozguner U. A control engineer's guide to sliding mode control[J]. IEEE Trans. on Control Systems, 1999,7(3): 328-342.
[2] ZHAO Dongya, LI Shaoyuan, Zhu Quanmin. Output feedback terminal sliding mode control for a class of second order nonlinear systems[J]. Asian Journal of Control, 2013, 15(1):237-247.
[3] 华森, 张天平, 朱秋琴, 等. 带有未知死区的机器人自适应滑模控制[J]. 中南大学学报(自然科学版), 2009, 40(增刊1):102-107.HUA Sen, ZHANG Tianping, ZHU Qiuqin, et al. Adaptive sliding mode control of robot manipulators with unknown dead-zone[J]. Journal of Central South University (Science and Technology), 2009, 40(Suppl1): 102-107.
[4] WU Zhaojing, XIE Xuejun, ZHANG Siying. Adaptive backstepping controller design using stochastic small-gain theorem[J]. Automatica, 2007, 43: 608-620.
[5] MA Ruicheng, ZHAO Jun. Backstepping design for global stabilization of switched nonlinear systems in lower triangular form under arbitrary switchings[J]. Automatica, 2010, 46:1819-1823.
[6] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407-418.LIU Jinkun, SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory &Applications. 2007, 24(3): 407-418.
[7] 李浩, 窦丽华, 苏中. 非匹配不确定系统的自适应反步非奇异快速终端滑模控制[J]. 控制与决策, 2012, 27(10): 1-5.LI Hao, DOU Lihua, SU Zhong. Adaptive backstepping non-singular fast terminal sliding mode control for mismatched uncertain systems[J]. Control and Decision, 2012, 27(10): 1-5.
[8] 廖煜雷, 万磊, 庄佳园. 欠驱动船路径跟踪的反演自适应动态滑模控制方法[J]. 中南大学学报(自然科学版), 2012, 43(7):2655-2661.LIAO Yulei, WAN Lei, ZHUANG Jiayuan. Backstepping adaptive dynamical sliding mode control method for path following of underactuated surface vessel[J]. Journal of Central South University (Science and Technology), 2012, 43(7):2655-2661.
[9] Farrell J A, Polycarpou M, Sharma M, et al. Command filtered backstepping[J]. IEEE Transactions on Automatic Control, 2009,54(6): 1391-1395.
[10] Swaroop S, Hedrick J K, Yip P P, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Trans on Automatic Control, 2000, 45(10): 1893-1899.
[11] 王坚浩, 胡剑波. 不确定非线性系统的自适应反推高阶终端滑模控制[J]. 控制与决策, 2012, 27(3): 413-418.WANG Jianhao, HU Jianbo. Adaptive backstepping high-order terminal sliding mode control for uncertain nonlinear systems[J].Control and Decision, 2012, 27(3): 413-418.
[12] 蒲明, 吴庆宪, 姜长生, 等. 非匹配不确定高阶非线性系统的滑模控制新方法[J]. 控制理论与应用, 2012, 29(6): 708-714.PU Ming, WU Qingxian, JIANG Changsheng, et al. New method of sliding-mode for higher order nonlinear system with mismatched uncertainties[J]. Control Theory & Applications,2012, 29(6): 708-714.
[13] Harl N, Balakrishnan S N. Reentry terminal guidance through sliding mode control[J]. Journal of Guidance, Control and Dynamics, 2010, 33(1): 186-199.
[14] Kim J, Oh S, Cho D, et al. Robust discrete-time variable structure control methods[J]. Journal of Dynamic Systems,Measurement, and Control, 2000, 122(12): 766-775.
[15] Chang J L. Robust discrete-time model reference sliding mode controller design with state and disturbances estimation[J]. IEEE Trans on Industrial Electronics, 2008, 55(11): 4065-4074.
[16] Chen W H. A nonlinear disturbance observer for robotic manipulators[J]. IEEE Trans on Industrial Electronics, 2000,47(4): 932-938.
[17] Cunha J P V S, Costa R R, Lizarralde F, et al. Peaking free variable structure control of uncertain linear systems based on a high gain observer[J]. Automatica, 2009, 45(5): 1156-1164.
[18] 宋超, 赵国荣, 盖俊峰. 基于非线性干扰观测器的高超声速飞行器反演滑模控制[J]. 系统工程与电子技术, 2012, 34(6):1231-1234.SONG Chao, ZHAO Guorong, GAI Junfeng. Sliding mode backstepping control for hypersonic aircraft based on nonlinear disturbance observer[J]. Systems Engineering and Electronics,2012, 34(6): 1231-1234.
[19] 蒲明, 吴庆宪, 姜长生, 等. 基于非线性干扰观测器的二阶动态Terminal 滑模在近空间飞行器控制中的应用[J]. 东南大学学报(自然科学版), 2009, 39(S1): 68-75.PU Ming, WU Qingxian, JIANG Changsheng, et al. Application of second-order dynamic terminal sliding mode control based on nonlinear disturbance observer to near space vehicle[J]. Journal of Southeast University (Natural Science Edition), 2009, 39(S1):68-75.
