基于AIS的元胞自动机模型的船舶交通流特征参数分析＊

冯宏祥 孔凡邨 肖英杰 杨小军

（上海海事大学商船学院 上海 201306）

2.2.2 速度 船舶速度是指某一水域内活动的或通过某一水域或通道的所有船舶的速度的分布范围和速度平均值.

0 引 言

船舶交通流研究是港口经济快速发展背景下提高船舶交通安全和效率的基础性问题之一.水上交通流研究起步较晚，其研究方法基本也是借鉴于陆上交通，但研究的广度和深度及取得的成果却远远不及道路交通工程学［1］.

作为海上交通工程学的重要基础之一，“船舶交通流密度－速度（流量）关系图”是基于“交通流速度和交通流密度之间的关系可简单地假定为线性关系”这一假设的，缺乏严密的理论依据和推导.随着我国水上交通的迅速发展，水上交通越来越繁忙，水上现象也越来越复杂，相对滞后的理论给一些复杂交通现象的解释带来了困难.

20世纪90年代以来，元胞自动机交通流模型（cellular automaton model，CA）一直受到交通学者的广泛关注，被认为是一种新的交通动力学模型.相对于其它模型，CA模型保留了交通系统的非线性特征，易于计算机程序实现，并能灵活地修改规则以考虑各种实际的交通状况，因此近年来被广泛地应用于物理学、交通工程学等领域［2－11］.基于CA 模型的以上优点，本文尝试利用该模型模拟航道船舶交通流，从机制上分析“船舶交通流密度－速度（流量）关系图”以及航道堵塞的形成和规律，开辟一条航道堵塞控制与研究的新路线.

1 模 型

根据文献［2］的模型，船舶ship（X，L，V）随机分布在长度为Lwaterway的一维离散元胞链上，具有位置X、长度L、速度V3类属性.通过AIS通讯，每艘船舶可以接收到周围其他船舶在t时刻的距离（位置）、速度、长度、CPA，以及船名等必要的避碰信息.基于这些信息，可以精确地判断t＋1时刻这些船舶的距离（位置）、速度、与本船的相对位置关系以及是否构成碰撞危险等信息，从而决定本船在t时刻的行动.

每个元胞最多只能同时被一艘船舶占据，Xi（t）∈｛0，1｝.每艘船舶占据相邻的 Li（t）个元胞，Li（t）∈｛1，…，Lmax｝.Vi（t）第i艘船舶在t时刻的速度，Vi（t）∈｛0，1，…，Vmax｝；di（t）为第i艘船舶与前方船舶间的距离

在开放性边界条件下，在每个离散的t→t＋1时间步，船舶状态按如下规则并行同步更新.

1）加速过程

2）减速过程

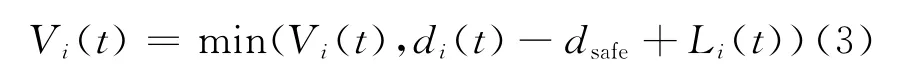
3）随机慢化

4）位置及速度更新

原船舶尺寸、位置及速度

新船舶尺寸、位置及速度

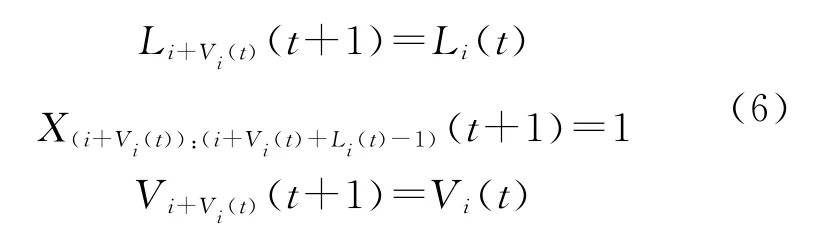
当Li（t）＝1，且不考虑船舶之间的安全距离和相对速度时（即没有AIS信息），本模型退化为经典的 NaSch（Nagel－Schreckenberg）模型.

2 模 拟

2.1 参数的确定

假设某单向航道长30nmile，航道中船舶尺度L∈［90，300］，m；速度V∈［10，16］，kn.航道内船舶不得追越或2船并排行驶.

2.1.1 元胞尺寸及参数的确定 根据文献［2］的讨论，本文取每个基本元胞的长度为30m.那么，航道长度为1 852个元胞；航道船舶尺度L∈［3，10］，速度V∈［10，16］.船舶更新步长取60s，运行周期为1d即1 440个步长.

2.1.2 船舶产生模型 根据船舶交通流实态观测，船舶的到达率服从爱尔朗分布，船头时距服从负指数分布，船长及船速服从正态分布.

2.1.3 船舶领域理论与安全距离 根据文献［2］的讨论，本文取每艘船舶与其他船舶的最小安全距离

式中：dsafe1，dsafe2和dsafe3分别为本船与前船、邻道前船、邻道后船之间的安全距离；Lownship为本船船长；Lforeship为前船船长.

2.2 交通流特征的基本参特征数

2.2.1 密度 船舶密度是指某一瞬间单位面积水域内的船舶数量.

2.2.2 速度 船舶速度是指某一水域内活动的或通过某一水域或通道的所有船舶的速度的分布范围和速度平均值.

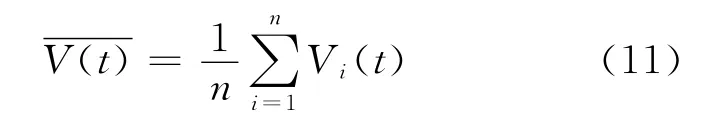
2.2.3 交通量 船舶交通量是指某一时间内通过水域中某一地点的所有船舶的数目（艘次）.

式（12）适用于所有的交通流理论，交通流研究的目的就是在上述交通流关系式的基本框架下，进一步挖掘和发现符合实际交通现象和交通规律的流量（速度）－密度关系.因此，往往只要给定了一个新的流量（速度）－密度关系式，就相当于建立了一个新的交通流模型.

2.3 模拟

根据上述模型及条件进行仿真实验以探求航道船舶流量与船舶密度、船舶速度之间的关系.实验中，航道初始状态为空闲，即没有船舶，船舶到达率为1艘／min，随机慢化概率为0.25.运行时航道长度设为2 052个元胞，然后去掉前20个以消除暂态的影响.假设运行300个步长时航道长度1 200个元胞处出现意外，船速减到0，意外持续500个步长后恢复正常.取30个样本以最大程度地消除随机因素的影响.

图1为基于AIS的CA船舶交通流模型的时空斑图；图2为基于AIS的CA船舶交通流模型的航道堵塞及恢复时空斑图.图1和图2中，横坐标为时间步长，方向从左向右，纵坐标为航道空间，方向从上到下.图1中，航道中的船舶随着时间的推移并行向下游更新船位，其空间轨迹呈现出流体特征；图2中的某船舶运行了300个步长后在1 200长度元胞处出现故障停车，导致航道堵塞，交通流聚集波迅速向上游传播，500个步长后该船舶恢复正常，堵塞的交通流开始消散.

图1 船舶交通流时空斑图（n＝1 852，航道初始状态有0艘船舶，船舶到达率为1，p＝0.25）

图2 船舶交通流航道堵塞－恢复时空斑图（n＝1 852，航道初始状态有0艘船舶，船舶到达率为1，p＝0.25，运行300个步长后1 200处发生事故，事故持续500个步长）

图3为基于AIS的CA船舶交通流密度－流量关系图30个样本的叠加图；图4为基于AIS的CA船舶交通流密度－速度关系图30个样本的叠加图.从图3和图4可以看出，每个模拟样本的密度－速度（流量）分布有明显的相同规律.

图3 船舶密度－流量关系图

图4 船舶密度－速度关系图

3 船舶流量（速度）－密度图的三相分析

3.1 船舶交通流的相态和相变

2.4 中根据模型仿真模拟得到的密度与速度（流量）的非线性关系和传统的至今仍被海上交通工程领域广泛沿用的“线性平衡速度－密度关系”有着明显的不同（见图3和图4）.下面取一个样本对密度－速度（流量）的关系进行分析.

从图5和图6可以看到，在整个交通流从自由流—集结—消散—自由流变化的过程中，船舶流存在自由流（F）、同步流（S）和拥挤流（J）3种相态，其转换应该存在从自由流与同步流（F↔S）和同步流与拥挤流（S↔J）相互转换的4个过程.

图5 流量－密度散点图

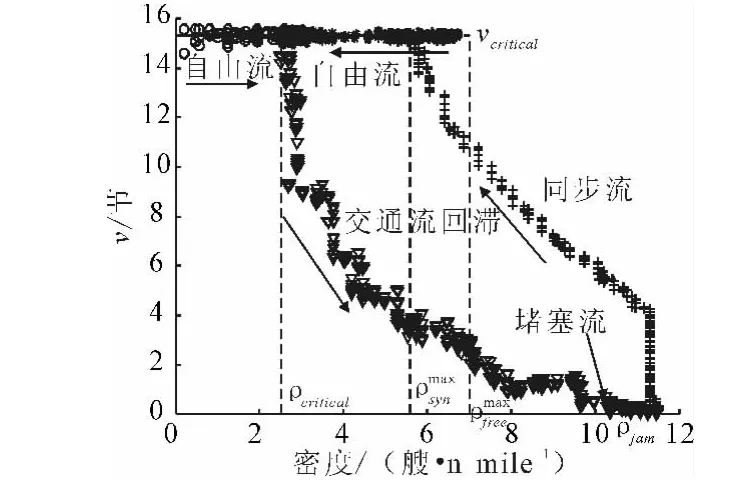
图6 速度－密度关系图

3.2 船舶交通流的三相分析

图5和图6中，当船舶密度小于2.5nmile时，船舶交通流处于自由状态，船舶流量随着密度的增大而线性增加，速度则呈带状分布，在15.3kn附近波动.

随着船舶密度的继续增大，交通流进入同步流状态，流量－密度图开始分化为2个部分，上面部分继续随密度线性增加，在密度约为3艘／海里时达到极大值，船舶流量也到达极大流量，下部分呈二维弥散分布；同时，速度开始随着密度的增大而迅速下降.

自由船舶流的临界速度，即图5中自由船舶流和拥挤船舶流分界线的斜率可由下式确定

随着船舶流的聚集，船舶密度进一步增大，船舶流速度继续下降.当密度达到最大（即导致堵塞的密度ρjam）时，速度降低到零附近，此时，船舶流处于走走停停的阻塞状态.当然，在实际的船舶交通流组织和管理实践中并不允许出现这种影响极其严重的极端状态，但是通过模拟分析，可以得到船舶进出航道调度的边界阈值.

船舶交通流的集结波波速可由下式确定

当导致航道阻塞的因素消失时，阻塞的船舶流开始启动.此时，虽然船舶流的速度较低，但由于船舶密度很大，因此船舶流量急剧增大，并迅速恢复到自由流状态.

船舶交通流的消散波波速可由下式确定

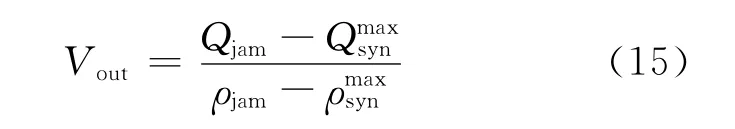
由于已启动的密度很高的船舶流前方畅通无阻，船舶间处于无约束的自由状态，当船舶流速度恢复至自由速度时，船舶迅速线性增大到最大值.之后，随着阻滞的船舶流逐渐退出，船舶流量随着船舶密度的回归而线性下降至正常状态.

从以上分析可以看到，船舶交通流的消散不是其集结的简单逆过程，船舶自由流向拥挤流相变时的密度往往高于相反方向相变时的密度，即存在着就现交通流回滞现象（hysteresis）.

4 结束语

本文通过基于AIS的元胞自动机船舶交通流模型模拟了航道中船舶流微观的行为，统计得到了船舶密度－速度（流量）的关系图，研究发现：（1）微观模拟的船舶密度－速度（流量）的关系图与海上交通工程学中应用的“线性平衡速度－密度关系图”存在着明显的差异；（2）应用微观模拟的船舶密度－速度（流量）的关系图可以将船舶交通流分为自由流、同步流和拥挤流三种相态，相态的转换存在从自由流与同步流（F↔S）和同步流与拥挤流（S↔J）相互转换的四个过程；（3）应用微观模拟的船舶密度－速度（流量）的关系图可以求取航道船舶交通流的最大自由速度、堵塞密度、最大流量密度、聚集波波速、消散波波速等.

目前，海上交通工程的理论还不完善，理论和实际的结合也不够紧密.由于CA模型易于计算机程序实现，其规则可根据实际交通状况进行修改，在船舶交通流研究中有较好的应用前景.

［1］吴兆麟，朱 军.海上交通工程［M］.大连：大连海事大学出版社，2004.

［2］冯宏祥，肖英杰，孔凡邨，等.基于船舶自动识别系统的元胞自动机局部缩减航道通过能力模型［J］.上海海事大学学报，2013，34（3）：22－26，31.

［3］邓建华.基于元胞自动机的自行车流蛇行、穿插模型［J］.武汉理工大学学报：交通科学与工程版，2011，35（1）：198－200.

［4］ZHANG S T，CHEN Y C.Simulation for influence of train failure on railway traffic flow and research on train operation adjusting strategies using cellular automata［J］.Physica A：Statistical Mechanics and Its Applications，2011，390（21／22）：3710－3718.

［5］HAN Y S，KO S K.Analysis of a cellular automaton model for car traffic with a junction［J］.Theoretical Computer Science，2012，450：54－67.

［6］TIAN J，YUAN Z，TREIBER M，et al.Cellular automaton model within the fundamental－diagram approach reproducing some findings of the three－phase theory［J］.Physica A：Statistical Mechanics and Its Applications，2012，391（11）：3129－3139.

［7］VASIC J，RUSKIN H J.Cellular automata simulation of traffic including cars and bicycles［J］.Physica A：Statistical Mechanics and Its Applications，2012，391（8）：2720－2729.

［8］YELDANÖ，COLORNI A，LUE A，RODARO E.A stochastic continuous cellular automata traffic flow model with a multi－agent fuzzy system［J］.Procedia－Social and Behavioral Sciences，2012，54：1350－1359.

［9］LIU J X，FENG Z，WANG M Q.Simulation of waterway traffic flow at harbor based on the ship behavior and cellular automata ［C］.Proceedings－International Conference on Artificial Intelligence and Computational Intelligence，AICI 2010；Los Alamitos，CA：IEEE Computer Society，2010：543－546.

［10］QU X，MENG Q.Development and applications of a simulation model for vessels in the Singapore Straits［J］.Expert Systems with Applications，2012，39（9）：8430－8438.

［11］李新刚.基于元胞自动机模型的交通系统微观建模与特性研究［D］.北京：北京交通大学，2008.