高速铁路钢轨力学模型的应用与合理性分析
2014-04-11崔瀚钰上海铁路局科研所
崔瀚钰 上海铁路局科研所
高速铁路钢轨力学模型的应用与合理性分析
崔瀚钰 上海铁路局科研所
在利用有限元软件对钢轨进行力学分析时,对钢轨模型的建立提出了两种不同的描述方式,建立了采用梁单元模拟钢轨和实体单元模拟钢轨的两种有限元力学模型。计算结果表明,对不同问题进行求解时需要采用合理的钢轨模型描述方式。在误差允许的条件下,解决轨道结构大系统问题时,采用传统的梁单元模拟钢轨,可以减少计算量,方便运算;在对钢轨自身内部的受力情况进行分析时,采用实体单元模拟钢轨,可以较好地反应其内部应力的变化。需要注意的是,边界条件及外部作用对实体单元模拟钢轨这一方式的影响较大。
钢轨;梁单元;实体单元;有限元
近年来,随着我国高速铁路的不断发展,列车的速度及运量都在不断地提高,列车车轮与钢轨之间的作用越来越强烈,轨道结构的破坏问题随之显得越来越突出,对铁路轨道的质量也就提出了更高的要求。因此在进行轨道结构的设计、养护及维修时,充分了解轨道结构各部件的应力和变形,对轨道进行力学分析是必不可少的。而由于轨道结构的不平顺、轨道部件的相互匹配、轨道结构动力响应等诸多问题的影响最终都能体现在与车轮直接接触的钢轨上,因此,本文主要针对钢轨的力学分析问题进行阐述。
1 研究背景
钢轨是铁路轨道结构最重要的组成部件,它的实际受力状况十分复杂。它直接与车轮接触,承受上部传来的巨大的轮载作用而产生弯曲、扭转应力,又会受到轮轨接触应力、温度应力等作用力的影响,进而产生弯曲、扭转、剪切等变形。经典的轨道力学分析方法在对轨道结构进行分析时,通常基于连续弹性基础梁理论和连续弹性点支承理论,将钢轨描述为无限长梁,通过扣件与下部轨枕连接,轨枕、扣件对钢轨的支承描述为连续弹性支承或点支承。但上述方法在求解钢轨应力时,不能合理反应出钢轨的局部受力问题,存在着很大的缺陷,计算结果精确度较低,已经越来越难以满足高速铁路对轨道结构更高精度的要求。
随着计算机技术的不断进步,有限元及数值分析方法的不断改进,工程中复杂问题的计算变得更为简单。利用有限元分析软件,我们可以建立与实际更为相近的轨道结构模型,得到更为合理、精确地分析数据。
2 钢轨建模
目前在分析轨道结构力学问题时,大部分采用的依旧是原先的简化方法,即基于欧拉梁理论和Timoshenko梁结构理论,采用二维或三维线性梁单元来模拟钢轨单元,采用弹簧单元来模拟扣件。而事实上,钢轨支承于轨枕之上,其支承距离正常在0.55m~0.66m之间,轨枕支承以及扣件并非单点作用于钢轨,因此,将钢轨视为线性长梁以及将扣件、轨枕作用看成点支承弹簧是否合理、精确,值得进一步商榷。
而利用有限元分析软件,我们可以建立更为贴合实际状态的钢轨实体有限元力学模型。其中,钢轨用实体(工字型)单元直接模拟,钢轨下部直接支承于扣件弹性垫板上,将扣件、轨枕系统对钢轨的作用考虑为线性均布弹簧模式。
3 计算结果对比及精确性分析
计算参数:
(1)钢轨:采用60kg/m钢轨,其弹性模量为2.1×105MPa,泊松比为0.3,线膨胀系数11.8×10-6/℃,密度7830kg/m3。
(2)扣件:取扣件弹性垫板的静刚度为22.5kN/mm,扣件间距0.65m。
为方便计算,不失一般性地,本文只针对钢轨在单点作用下正截面拉压应力的受力进行分析。同时为了消除边界效应的影响,结合以往经验,取13跨钢轨长度为计算长度。单个轮载作用力结合17t轴重,考虑3倍的动载值为22.5kN,作用点为钢轨长度中间位置(即跨中)。梁单元钢轨模型中,扣件视为单支弹簧;实体单元钢轨模型中,扣件系统视为均布弹簧,其刚度平均分配,下部结构对弹簧端的影响视为全约束。并假设钢轨长度中间位置为坐标0点,分析对比跨中0.65m长钢轨受力情况。
3.1 钢轨截面拉压应力对比
如图1~4所示,对比了梁单元模拟钢轨和实体单元模拟钢轨两种分析建模方式下,钢轨在0mm(钢轨中部位置)、62.5mm、250mm、325mm(扣件中部位置)四处的截面应力。图中,横轴表示应力值(单位MPa),纵轴表示钢轨高度位置(轨底为0,单位mm)。
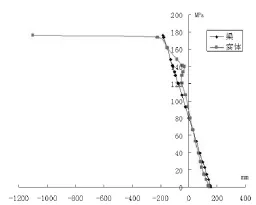
图1 0mm处截面应力分布对比
首先,我们分析跨中0mm处和扣件支承325mm两个位置,即钢轨外力作用点位置和钢轨下部结构对其作用位置的力学状态。
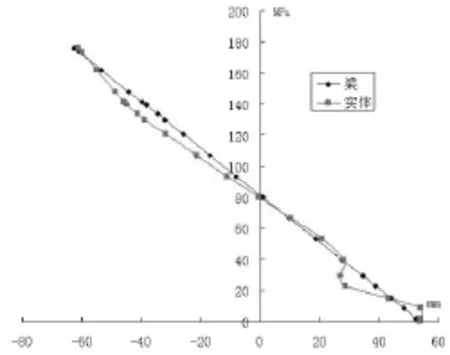
图2 325mm处截面应力分布对比
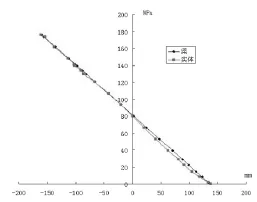
图3 62.5mm处截面应力分布对比
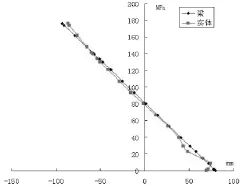
图4 250mm处截面应力分布对比
我们不难看出,在这两处,两种方法计算得到的截面应力分布及大小差别相对是较大的。可见,外界因素对钢轨内部应力分布的偏差会带来较大的影响,这与建模时外部作用力位置及弹簧约束的表示方式是有很大关系。此外,图1中利用实体单元模拟钢轨时,压应力出现了一个很大的值,这是由于单点作用力产生了应力的集中引起的,而采用梁单元模拟钢轨时就很好地避免了这个问题。在两个外力作用点中间,我们选取了62.5mm、250mm两个位置来分析。
在这两个位置处,我们发现两种建模方法分析得到的截面应力,其应力分布及其大小均比较接近,差别不大,说明两种建模方法都是可以的。
此外,实体单元建模由于节点之间存在微小的相对位移,应力变化是非线性的,而梁单元建模得到的结果则基本是线性的。
综上所述,在建立整个轨道结构大系统时,若不单纯分析钢轨结构,采用梁单元模拟钢轨是可行的,并且相较于实体单元模拟钢轨的建模方式,可以减少很多不必要的计算,并将误差控制在了允许范围之内。但是,在单纯分析钢轨内部的受力时,由于边界条件以及作用点位置等对其内部应力变化及分布影响较大,采用梁单元模拟钢轨的方法,其效果就相对较差了。这时我们就应当选择使用实体单元模拟钢轨建立的有限元分析模型。
3.2 钢轨拉压应力随纵向变化对比
考虑最大拉压应力的两种情况,即钢轨头部最大压应力及钢轨底部最大拉应力,仿真结果如图5~6所示。图中横轴表示应力点位置(单位mm),纵轴表示应力值(单位MPa)。
由计算结果可以看出,从整体上看,两种建模方式分析得到的应力在纵向上的变化趋势近似相同。在图5中,利用实体单元模拟钢轨时,在中部轨头位置存在着单点作用力,其应力集中也体现的比较明显,影响了附近点的压应力值,与采用梁单元模拟钢轨的方式得出的应力值数据存在着较大的偏差,但其两边位置的数值吻合得还是较好的。在图6中,对钢轨底部的拉应力进行分析时,在扣件位置处应力值会出现偏大得趋势,使得从整体上看,实体单元模拟钢轨的建模方式得到的拉应力值相对偏大。这是由于采用了均布弹簧,因为刚度分配的原因,下部弹簧对轨底的作用只体现在一定范围内,会导致整体约束力是要低于梁单元模拟方式采用的单个弹簧对节点的约束力的,从而使得钢轨变形较大,应力增大。
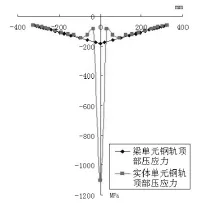
图5 梁单元与实体单元钢轨头部最大压应力对比
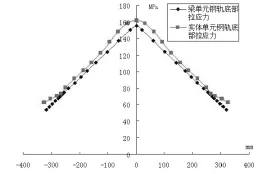
图6 梁单元与实体单元钢轨底部最大拉应力对比
4 结论
通过梁单元及实体单元建立钢轨的有限元模型对钢轨结构进行分析计算,对比计算结果,我们可以得出以下结论:
(1)在计算一般的轨道结构大系统时,利用梁单元模拟钢轨结构,将钢轨描述成梁是可行的。从整体上看,两种建模方式分析得出的钢轨的应力分布规律大致相同,只是在一些细节部位存在明显差异,在精度要求不高,允许一定误差的情况下,采用梁单元模拟钢轨,具有计算量小、计算方便的优势;
(2)在对钢轨单独分析其局部应力时,用实体单元进行建模则更为准确。实体单元可以较好地反应出钢轨诸多细部应力分布,对边界条件的作用反应较为敏感,而梁单元只能反映整个钢轨截面的变化情况,截面任意位置处的应力还需通过公式计算转化;
(3)弹簧的支承方式,如单点支承、均布支承,对钢轨的应力分布及大小有影响,需要根据具体情况采用合理的建模方式。
[1]金学松,温泽峰,王开云.钢轨磨耗型波磨计算模型与数值方法[J].交通运输工程学报,Vol5 No2,2005.06.
[2]杨罡,刘明光,李娜,屈志坚.钢轨电位分布模型及仿真[J].北京交通大学学报,2010.02.
[3]张渊,魏伟.基于有限元梁轨枕的轮轨高频振动模型[J].机械工程学报,2008.03.
[4]史颖刚.智能轨道检测仪的数学建模及其误差分析[D].大连理工大学,2006.
[5]李海锋,陈文,陈雯.高速铁路钢轨型面变化的跟踪观测及仿真分析[J].城市轨道交通研究. 2012.02.
[6]金学松,温泽峰,张卫华.轮对运动状态对轮轨滚动接触应力的影响[J].工程力学,2004.01.
[7]卜继玲,李芾,付茂海,黄运华.重载列车车辆轮轨作用研究[J].中国铁道科学,2005.05.
[8]黄志辉,柏友运.高速货车车轮摩擦力对钢轨承载区域影响的有限元分析[J].现代制造工程, 2009.05.
责任编辑:王华 徐伟人
来稿日期:2014-01-26
