车床主轴回转精度数字式单向测量法

张 丹 黄惟公 王 瑞 曾颖峰 西庆坤

(①四川工程职业技术学院，四川 德阳 618000；②西华大学机械工程与自动化学院，四川 成都 610039；③东方汽轮机有限公司风电事业部，四川 德阳618000)

车床主轴是决定工件或刀具位置并传递主要切削运动的重要部件，其精度直接影响着工件加工表面的形状精度和粗糙度。通过测量车床主轴回转误差运动，可以预测车床在理想加工条件下能达到的最小形状误差和粗糙度，分析判断加工误差产生的原因，诊断主轴出现的故障等[1-2]。因此主轴回转误差作为衡量车床性能的重要技术指标，如何开发具有实时性、针对性、高精度的车床主轴回转精度检测系统一直是车床研究的重要内容。

针对车床主轴回转精度的测量，早期的测量方法是采用简单易行的打表法，该方法会引入锥孔的偏心误差，不能反映工转状态下的回转误差，不适用于高速、高精密测量。而对于车床主轴回转误差的动态测量方法，文献[3]采用两路传感器分别检测车床主轴回转运动的径向误差和工件圆度，并用两路脉冲传感器检测主轴转角，产生采样控制信号，该方法使用了基圆发生器，其测试结果难以在各机床间进行比较。文献[4]提出了基于IRM和小波变换的圆度误差检测技术，可有效分离车床主轴回转误差与圆度误差，该方法数据处理过程繁杂。文献[5]利用双向法直接、同时采集电主轴外圆轮廓数据，应用数理统计的方法分离主轴的形状误差和回转误差，该方法使用了多路传感器，增加了测量成本，而且易受到结构和空间的限制，传感器的安装较困难。文献[6]提出了主轴回转精度的CCD测量系统，该系统容易在计算光斑重心时产生误差，对光源和电源有较高要求，环境因素对测量结果影响较大。

综合以上测量方法，本文考虑到车床主轴误差运动在轴向方向上的分量对加工表面的影响较小，可忽略不计，故只使用一个传感器布置在径向方向即可，此外可利用算法获得基圆，因此提出了一种输出处理简便、易于实现的数字式单向测量法对车床主轴回转精度进行动态测量的系统。

1 检测信号分析

车床主轴的理想回转轴线在空间中的位置是固定不变的，但由于轴颈、轴承的几何形状精度、轴绕曲、支承孔的误差及振动等因素，均会造成回转轴线在每一瞬时都是变化的，因此以回转轴各瞬时轴心线的平均位置作为理想轴线。由于回转轴线是看不见的，测量时通常选用高圆度的圆球作为基准面来体现回转轴线。如果基准球的轴心和回转轴线的轴心是一致的，那么通过基准球测量得到的误差就是回转轴的误差，然而回转轴线的不可见，不能保证基准球安装不存在偏心现象。车床主轴的回转误差运动是一个复杂的周期信号，其在径向上的分量直接影响工件表面的质量，因此仅在径向上布置位移传感器对径向跳动进行测量，此外基准球的表面形状也不能完全忽略，基于以上原因建立图1所示的检测车床主轴径向回转误差运动的方法。根据图1所示的几何图形可作出如下假定：O0为理想回转中心，Om为基准球的几何中心，Or为瞬时回转中心，e为基准球的安装偏心量，θ为瞬时误差运动的转角，r(θ)为某一瞬时的径向误差运动，Rm为基准球半径，s(θ)为基准球形状误差。

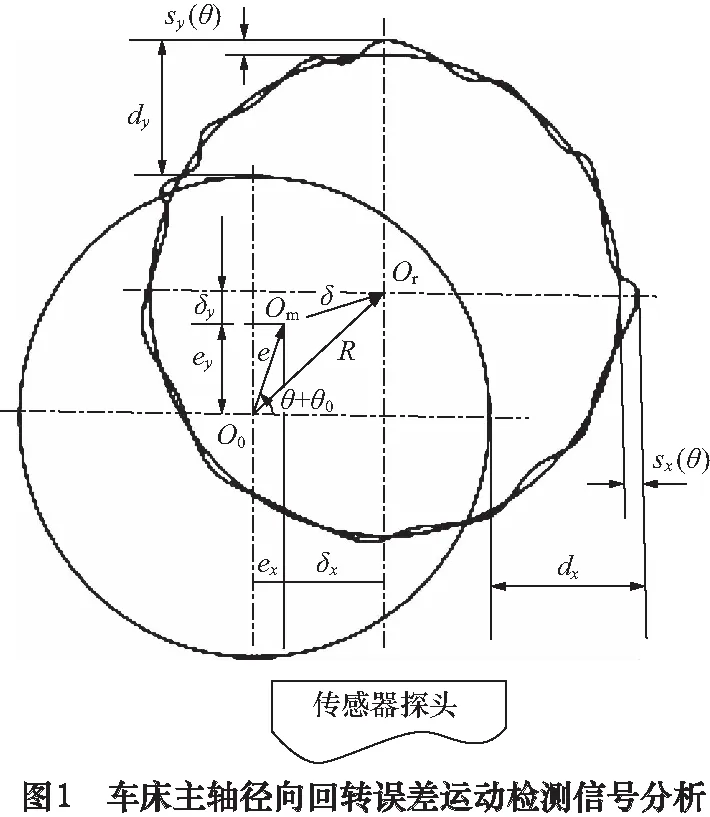
若基准球半径Rm远大于安装偏心误差e和径向回转误差r(θ)，根据几何图形的假定条件，建立传感器输出信号的数学模型：

dy=esinθ+ry(θ)+sy(θ)

(1)

式中：dy为传感器测量到的位移信号；ry(θ)为某一瞬时的径向误差运动在y方向的投影；sy(θ)为基准球的形状误差在y方向的投影。

从式(1)可看出，传感器所获得的数据由3个部分组成，即基准球安装偏心误差、主轴径向跳动误差、基准球形状误差。但评定车床主轴回转误差仅需要径向跳动误差，必须通过误差分离的手段将基准球的安装偏心误差和基准球的形状误差除去。由于该测量系统采用形状误差远小于回转误差运动的高圆度的圆球作为测量基准球，那么基准球的形状误差可忽略掉。

dy=esinθ+ry(θ)

(2)

从忽略了标准球的形状误差的式(2)可知，基准球安装偏心始终存在，则将基准球的安装偏心误差和主轴径向误差分离就成为检测径向误差运动的关键所在。基准球安装偏心误差esinθ是个正弦信号，可通过数字信号处理方法将该正弦信号滤除掉，这就实现了基准球安装偏心误差和主轴径向误差的分离，进而获得评定车床主轴回转误差的数据ry(θ)。

2 数字式单向测量法

2.1 测试原理

车床主轴瞬时中心Or的运动由于基准球安装偏心、表面形状误差的客观存在无法直接测得。基准球安装偏心的大小和方位即使针对的是相同的运行条件和同一根轴，也会出现dy不一样的情况。因此，必须要统一制订基准球的精度和偏心e的方位和大小，用于评价和比较回转轴运动状态的优劣，但这在实际中几乎是不可能实现的。国内外学者的研究表明，传感器测得的基准球安装偏心e所产生的信号是一次谐波分量，其频率正好与主轴的转速一致。数字式单向测量法的工作原理是：基准球跳动信号经位移传感器、信号调理模块、信号采集模块进入计算机，计算机用数字信号处理技术分离出位移信号中的偏心量e，得到接近真实的瞬时回转中心的运动信号，再将其叠加在一个人为确定的半价大小可调整的基圆上去形成圆图像，圆图像的数值评定结果就是主轴的回转精度。图2是数字式单向测量法原理图。

图2所示的数字式单向测量法与传统的测量方法相比有明显的优点：①该系统省去了基圆发生器，解决了基圆发生器在生产制造过程中给检测机床主轴回转精度带来的不便。②传统的测量法使用多孔圆码盘来确定车床的转速。本系统将多孔圆码盘取消掉，这是因为车床主轴在转一圈的过程中，可认定其转速变化是不大的，对数据采集模块采集到的数据通过快速傅里叶变换(FFT)后得到偏心误差e的频率fe，进而获得车床主轴的转速n。③传统的测量法使用光电传感器的输出信号控制A/D转换器的采样间隔和每转采样起始时刻，以便获取车床主轴在转一圈的过程中数据采集模块采集到的点数Nd。本系统将光电传感器取消掉， 利用式(3)计算出Nd。

(3)

式中：fs为数据采集模块的采样频率。

2.2 圆图像的产生

在数字式单向测量法中，用圆图像记录误差信号时，用算法产生基圆。若数据采集模块在车床主轴每转中采集到Nd个数据X(i)，i=0,1,2,…,Nd，只需加一个常量R(基圆半径)，再按照每个采样点所对应的角度，将它们分别分解成两个垂直方向的分量X(i)、Y(i)，即可完成被测信号与基圆的叠加，具体的算法如图3所示。由于算法产生的基圆所用的半径R不受测试设备的限制，所以很容易采用统一的基圆半径来评价测量结果。

2.3 圆图像的处理

圆图像是在一段时间内连续记录若干转误差而获得的。对车床主轴而言，圆图像既反映了主轴回转精度，又近似反映了工件表面轮廓形状，所以具有很好的直观性。总误差运动圆图像反映了误差运动的总体情况，而平均误差运动圆图像则反映了某种倾向性的误差运动规律。对圆图像的数值评定，通常采用包容法，即用两个正好包容误差运动圆图像的同心圆的半径差作为误差运动大小的评定值。目前国际上通用的4种评定圆度误差的方法为：最小二乘圆法(LSC)、最大内切圆法(MIC)、最小外接圆法(MCC)、最小区域法(MKS)。利用计算机软件编制相应的圆度评定程序，就能对采样数据作4种圆度评定，其评定结果就是主轴回转精度。主轴回转精度的评定实际上是主轴回转运动轨迹的圆度评定。

3 测量信号仿真

研究表明，车床主轴回转误差数字式单向测量法实际测量所得的数据为随机信号与某种基波的叠加[7]，因此可用式(4)来仿真回转误差。

X(t)=Asinωt+radm(t)

(4)

式中：radm(t)为随机数。

车床主轴回转误差数字式单向测量法的仿真结果如图4所示。图4a为回转误差时域图，对该原始数据采用FFT变换后得到幅频谱，如图4b所示；根据幅频谱可找到一个幅值最高的频率，该频率就是安装偏心量e所对应的频率；采用低通滤波的方法得到安装偏心所产生的一次谐波，如图4c所示；采用高通滤波的方法将与主轴转速同频率的偏心量消除，得到主轴回转运动误差时域信号，如图4d所示；同时，根据式(3)可求得原始数据的周期T，再以T截取图4d的一个整周期信号，利用图3所示的算法得到圆图象。

本文在相同的仿真条件下，针对同一组数据，根据4种评定圆度误差的算法分别编制了程序，图5所示为评定圆度误差的4种方法，并将相应的圆度误差值记录在表1中。

表1 基于LSC、MIC、MCC、MKS的圆度误差值

从表1可看出，4种圆度误差评定方法中，利用LSC、MIC、MCC对同一测量数据进行评定，其圆度误差值大小无规律，但是，对于每组测量数据，最小区域法得到的误差值都是最小的，这与理论分析是一致的。因此在后续的实验测量中，本文仅用最小区域法对圆度误差进行评定。

4 实验测量

4.1 测试系统的组成

在C616车床上利用数字式单向测量法进行主轴回转误差动态测量，具体的测试系统如图6所示。本系统由NI公司的数据采集卡PCI-6024E及其接线端子CB-68LP、电涡流式位移传感器(OD9000)及特制支架、通用PC机等部分组成。电涡流式位移传感器的探头通过随主轴旋转着的基准球拾取跳动信号(包括基准球安装偏心量和回转误差)，采集到的跳动信号经过调理电路放大、滤波后送给数据采集卡进行A/D转换和数据传输处理，最后送入到计算机进行数据处理和圆度评定。

4.2 测试结果处理与分析

测试条件：车床型号C616；主轴转速360 r/min；室温20±0.5 ℃；基准球尺寸φ10.18 mm；电涡流传感器的探头距基准球最近的位置为0.7 mm。

测试软件：LabWindows。

用本文方法对车床主轴回转误差进行测量，取fs=1 024 Hz，圆度误差用最小区域法评定，图7为主轴回转误差数据处理过程。从图7a、图7b可看出，原始采样信号中包含着主轴安装偏心信号和高频干扰信号；利用数字滤波器滤波得到主轴回转误差信号如图7e所示；将分离了偏心量的时域信号进行FFT变换后得到幅频谱，从图7f看出，与主轴回转信号同频率的偏心量已经基本消除。

根据误差理论分析，用单个样本来评定误差较大，增加所取的样本数可提高测量精度。根据本实验的具体情况，取10个样本数(本文指回转圈数)作为分析对象。当车床主轴转速为360 r/min、530 r/min、750 r/min时，采用本文方法测量10圈主轴回转精度的圆度误差值并求其均值，然后在相同的实验条件下，利用重庆迪佳科技有限公司的便携式DJ-HZ-1型机床回转精度测量分析仪进行验证，得到两种测量方法下

的主轴回转精度，如表2所示。

表2 C616车床主轴回转精度实测结果对比

注：*为均值。

从表2可看出，本文提出的数字式单向测量法的测量结果与DJ-HZ-1型机床回转精度测量分析仪的测量结果基本吻合，主轴回转精度随着转速的提高有增大趋势，这与实际情况相符合。因此可以说本文提出的测量方法能方便、准确、可靠地测量主轴回转误差。

5 结语

车床主轴回转误差数字式单向测量法，采用单个传感器进行测量，避免了多个传感器在测量时由于性能不一致造成的计算误差，此外通过数字滤波法实现了基准球安装偏心量与主轴径向回转误差的有效分离，从而提高了系统的测量精度。实验结果表明，该方法的测量结果与DJ-HZ-1型机床回转精度测量分析仪的测量结果基本吻合，说明此方法有效。但是，本文测量得到的主轴回转误差测量结果是在车床空载运行下得到的，没有考虑切削力对主轴回转误差的影响，这是本测量方法在今后需进一步研究的地方。

[1]洪迈生.回转误差运动的测量[J].宇航计测技术,1985(3):15-23,40.

[2]黄惟公,董仲林.机床主轴回转精度数字测量法及其仿真[J].四川工业学院学报,1999,18(3):1-4.

[3]王春海,陈明,石望远.车床加工中圆度误差在线检测技术[J] .航空精密制造技术,2004,40(4):41-42,46.

[4]张玉梅,左春柽,李春芳.基于IRM和小波变换的圆度误差在线检测技术[J].农业机械学报,2009,40(7):212-216.

[5]伍良生,王永宾,周大帅.基于LabVIEW的电主轴径向回转误差测量技术[J].制造技术与机床,2009(9): 13-17.

[6]王卫东,翟超,陈柯.机床主轴回转精度的CCD测量系统[J].计量学报,2006,27(1):18-21.

[7]黄惟公,曾盛绰.机械工程测试技术与信号分析[M].重庆:重庆大学出版社,2002.