船用多功能数控机床关键运动副结构稳定性分析
2014-04-09孙椰望张甲英徐滨士
孙椰望, 张甲英, 赵 刚, 徐滨士
(1. 北京理工大学机械与车辆学院, 北京 100081; 2. 装甲兵工程学院装备再制造技术国防科技重点实验室, 北京 100072; 3. 装甲兵工程学院装备再制造工程系,北京 100072)
随着国内舰船装备的快速发展,保障舰船长期正常的运行关系到舰船行业的重要经济与战略利益[1]。鉴于舰船工作环境的局限性,为了实现舰船装备损坏零部件的快速保障要求,设计制造船用多功能数控机床成为增强舰船装备快速保障能力的重要任务。针对舰船装备的易损小型零件及其再制造零件的快速加工技术要求,笔者团队以机床的可靠性和环境适用性为宗旨,设计制造了集车、铣、车铣、铣车等加工工艺于一体的船用多功能数控机床。
然而,船用机床与通用机床最大的区别在于舰船海洋工作环境下的波浪载荷摇荡特点[2-3]。船用机床除了能够实现所需多种零件的快速加工外,还需要具备海洋工作环境下的动态稳定性。特别是船用功能数控机床的关键运动副处于单自由度运动状态,并且其特有的部件装配结构造成导轨滑块所承受的负载较为突出,其结构稳定性分析成为机床整体性能评价的关键环节。
1 船用机床的波浪振动环境分析
船用机床固定于舰船上,舰船的摇荡运动直接影响到机床的结构稳定性。舰船运行过程的研究表明:横摇运动直接关系到舰船的倾覆和航行安全性[4-5]。同时,舰船在海洋中行驶的加速度、横摇幅值和横摇周期直接影响到船员的工作能力,特别是人的内耳腔对线加速度和角加速度很敏感,稍大加速度容易刺激这些身体系统,从而造成人员晕船。通常情况下,当舰船摇荡加速度大于0.1g,横摇周期小于10 s,横摇角大于4°时,人的运动能力将会迅速下降[6-7]。因此,船用机床在舰船运行中正常工作应该基于船员的生理适应环境。
图1所示机床运行环境存在3个主要坐标系:空间固定坐标系O-ζηξ以静止海平面为基准坐标,主要描述波浪的运动状况和舰船遭遇波浪的状态;运动坐标系o-xyz以舰船为基准坐标系,始终与舰船结构方向一致,并伴随舰船的摇荡而变化,描述舰船受到波浪扰动的运动状态;机床结构固定坐标系G-XYZ以机床和舰船的结构重心为基准原点,X、Y、Z始终保持横向水平、竖直向上和纵向水平方向,通过与运动坐标系o-xyz的比较确定机床的摇荡运动,当舰船在静止水面行驶时,o-xyz与G-XYZ具备同向性。
图1所示船用多功能数控机床具备铣削、车削、铣车和车铣功能。机床工作过程中具有铣削立柱的Z2向移动、车削托板的Z1向移动以及铣削刀具和车削刀具的进给运动。在这些运动中,Z1和Z2的导轨滑块分别承受立柱重力和托板重力的负载,在受到舰船摇荡力作用时,其动态稳定性受到的影响较大。
舰船波浪载荷的动态稳定性研究[4,8]表明,舰船行驶过程中具备6个自由度的摇荡运动特点:横摇、纵摇、首摇、横荡、纵荡和垂荡。其中,受到舰船操作和海况的影响,横摇运动成为舰船设备在波浪载荷工作环境下的主要摇荡形式[9-10]。同时,机床固定于舰船上,为了避免横摇运动对机床运行过程的较大影响,需要结合船用机床的结构特点,避免机床主要运动与横摇运动的叠加。因此,机床在舰船上布置时,舰船的横摇运动方向应该与机床GZ方向成垂直状态。

图1 船用多功能数控机床结构方案示意图
2 船用机床关键运动副横摇力分析
根据图1机床的结构特点可知:当机床横摇时,由于铣削立柱的重量以及Z2滑块导轨运动副负载较大,因此Z2滑块导轨运动副成为影响机床动态性能的主要部件。因船用机床固定于舰船上,所以其横摇运动参数与所在舰船的横摇参数一致,表1为船用多功能数控机床所在舰船的主要参数。

表1 船用多功能数控机床所在舰船主要参数
根据表1参数和CCS(China Classification Society)钢制海船设计标准[11-13],得到机床所在舰船的横摇参数如下。
1) 横摇最大周期
(1)
式中:B为舰船宽度(m);φ为横摇角(rad)。
2) 最大横摇角
φmax=κ(62.5-1.25Tφ)/(B+75)=0.43(rad),
(2)
式中:κ为减摇系数,取1.0。
3) 最大横摇角加速度
βφmax=φmax(6.28/Tφ)2= 0.075 (rad/s2)。
(3)
4) 机床所在位置最大横摇线加速度
aφmax=βφmaxH=0.075×3.9=0.29 (m/s2),
(4)
式中:H为横摇转动半径(m)。
根据机床的横摇简谐运动可知:机床滑块导轨竖直方向主要受到立柱重力及其等效支反力作用;Z2滑块导轨运动副合外力为横摇切向的简谐横摇力,其最大受力位置为机床横摇初始位置和最大横摇位置,且横摇切向力为
F=ma=mHβ,
(5)
式中:m为机床立柱质量(mg);a为横摇线加速度(m/s2);β为横摇角加速度(rad/s2)。
根据计算得到的舰船横摇运动参数,船用机床布置位置高度为横摇转动半径H=3.9 m,机床立柱质量为m=700 kg,立柱重心高度h=431 mm,可知导轨滑块运动副受到的最大横摇力为
Fmax=maφmax=700×0.29=203(N)。
(6)
3 关键滑块导轨运动副受力分析
3.1 滑块导轨运动副性能设计
根据HG45CA滑块导轨运行标准,机床在具有振动的环境中,其运动加速度应该不大于0.5g[14]。机床设计的滑块导轨运行速度与时间关系如图2所示,其中,最大快速移动速度为vmax=0.2 m/s,设计加速至最大速度所用时间为t1=0.1 s,加速度a1=2 m/s2;最快减速至0 m/s所用时间为0.15 s,加速度a3=1.3 m/s2。

图2 滑块导轨运行速度与时间关系
机床立柱、导轨和滑块的相互布局位置如图3所示,其中,4个滑块布置位置尺寸l0=l1=320 mm,导轨长度l=1 500 mm,导轨行程为ls=1 450 mm,h=431 mm。

图3 机床立柱、导轨和滑块的相互布局位置
3.2 滑块导轨运动副运行负载分析
根据图2、3进行滑块导轨运动副的运行过程负载计算。
3.2.1 每个滑块的垂向负载
1) 加速度为a2运行时,4个滑块的垂向负荷主要为立柱的重量,即
p12=p22=p32=p42=mg/4=1 678.25(N),
(7)
式中:p12、p22、p32、p42分别为图3(a)中1、2、3、4滑块在加速度为a2时的垂向负荷(N)。
2) 加速度为a1向左加速运行时,滑块垂向负荷为
pa11=pa41=p12-ma1h/(2l0)=755(N),
(8)
pa21=pa31=p22+ma1h/(2l0)=2 601.61(N),
(9)
式中:pa11、pa21、pa31、pa41分别为图3(a)中1、2、3、4滑块在加速度为a1时的垂向负荷(N)。
3) 加速度为a3向左减速运行时,滑块垂向负荷为
pa13=pa43=p12+ma3h/(2l0)=2 239.01(N),
(10)
pa23=pa33=p22-ma3h/(2l0)=1 117.49(N),
(11)
式中:pa13、pa23、pa33、pa43分别为图3(a)中1、2、3、4滑块在加速度为a3时的垂向负荷(N)。
4) 向右运动时,滑块垂向负荷为
pa11=pa41=p12+ma1h/(2l0)=2 601.6(N),
(12)
pa21=pa31=p22-ma1h/(2l0)=754.89(N),
(13)
pa13=pa43=p12-ma3h/(2l0)=1 117.49(N),
(14)
pa23=pa33=p22+ma3h/(2l0)=2 239.01(N)。
(15)
根据计算数据可知:滑块导轨运动副向左运动时,滑块垂向最大负载为加速度运行时的右侧2和3滑块负荷,即
pa21=pa31=p22+ma1h/(2l0)=2 601.61(N);
(16)
滑块导轨运动副向右运动时,滑块垂向最大负荷为加速度运动时的左侧1和4滑块负荷,即
pa11=pa41=p12+ma1h/(2l0)=2 601.61(N)。
(17)
3.2.2 每个滑块的横摇运动侧向负载
1) 横摇力侧向负载
根据滑块导轨副的加速和减速运行载荷计算分析可知:当机床处于横摇状态时,单个滑块承受的最大侧向载荷为
pmax=Fmaxh/(2l1)=259(N)。
(18)
2) 铣削力侧向负载
根据铣削加工工程分析,该类型机床常用的最大铣削切向力为FXmax=100 N,于是根据图4所示可以计算得到机床Z2滑块导轨副的最大侧向铣削力负载为
pFXmax=596FXmax/(2l1)=93.125(N)。
(19)

图4 船用机床最大铣削工件位置图
4 滑块导轨运动副结构强度分析
4.1 滑块导轨运动副适居性横摇环境下静态校核
机床滑块导轨运动副静态安全系数为
fs=Co/pmax=87 700/2 601.61=33.7,
(20)
式中:pmax为单个滑块导轨运动副的最大负荷(N);C0为单个滑块导轨运动副的基本额定静载荷(N)。
滑块导轨运动副的横摇运动的最大力矩为
Mmax=Fmaxh=87.5(N·m)。
(21)
单侧滑块滑块导轨运动副承载的最大横摇力矩为
MXmax=Mmax/2=43.8(N·m)。
(22)
单侧滑块导轨运动副承载的最大铣削力矩为
MFXmax=0.596FXmax/2=29.8(N·m)。
(23)
滑块导轨运动副的侧向力矩安全系数为
fM=MC/(MXmax+MFXmax)=
1 919/73.6=26,
(24)
式中:MC为单个滑块导轨运动副的许用横摇静力矩(N·m)。
计算安全系数远大于3.0~5.0的最低标准范围,所以船用多功能数控机床关键滑块导轨副能够满足工作环境下正常运行。
滑块导轨运行额定寿命为
Llmax= 50(C/(fwpmax))3=
50×[55 000/(2×2 601.61)]3=
59 053(km),
(25)
式中:C为单个滑块导轨运动副的基本额定动载荷(N);fw为受到冲击力和振动作用的负荷系数。
单个滑块导轨运动副的最大运行额定寿命为
Lhmax= 8.3Llmax/(lsn)=
8.3×59 053/(1.45×2)=
169 013.76(h),
(26)
式中:n为滑块每分钟往复次数。
计算结果表明:在最大的负荷下工作时,机床运行169 013.76 h必须进行导轨大修。
4.2 滑块导轨副横摇谐响应动态性能校核
为了进一步分析舰船设计横摇最大环境下机床关键滑块导轨副的动态性能,本文采用模态叠加法对船用滑块导轨系统进行波浪变频横摇力的谐响应动态性能分析。分析过程的边界条件按照工况情况进行导轨底面固定约束和横摇力矩设置,如图5所示。图5所示导轨滑块FEM模型为考虑导轨滑块运动副结合面特点的弹簧接触模型[15],弹簧刚度和阻尼比的参数按照试验模态得到数据进行设置。

图5 考虑结合面特点的滑块导轨谐响应分析模型
根据舰船振动特性研究成果[8-9,16]设置船用机床Z2向导轨滑块副FEM模型的变频横摇力矩载荷,如表2所示。分析结果如图6、7所示。
图6为滑块导轨的谐响应应力、位移和相位谱分析关系图。结果显示导轨滑块系统的相位响应在横摇力矩频率范围内没有出现变化,结合应力、位移与激发频率关系图的无峰值现象可知:横摇频率0.05~0.2 Hz内,滑块导轨运动副不存在共振现象。同时,由图6(a)可知:当横摇频率为0.065 Hz,即舰船横摇周期为13.3 s时,滑块导轨振动系统的谐响应应力最大。由于谐响应的力谱分析只能通过选择整个系统的关键区域进行显示,因此,为了进一步分析横摇周期为15.4 s的滑块导轨振动系统整体应力与变形情况,需进行单频激励下的动态分析,其结果如图7所示。

表2 滑块导轨系统谐响应变频力矩
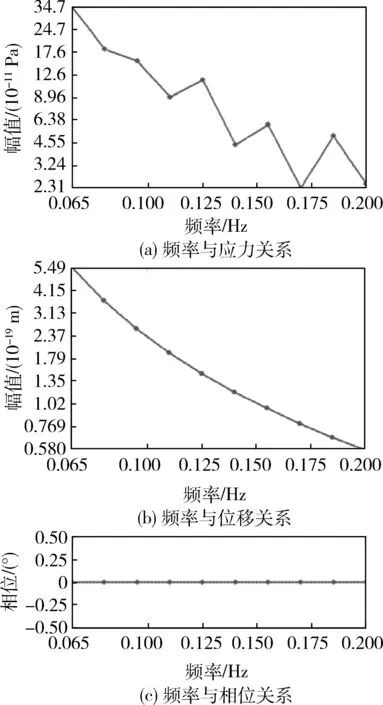
图6 谐响应谱分析
图7为滑块导轨系统在横摇频率为0.065 Hz时的谐响应应力和位移分析,结果表明:在受到最大横摇动载荷影响的情况下,船用多功能数控机床立柱Z2导轨的最大应力为1.5×10-8Pa,最大变形为4.4×10-8m,最薄弱区域主要集中在滑块导轨的结合面处,但是最大应力和位移都远小于船用多功能数控机床的结构屈服应力220 MPa和运行精度1.0×10-6m的界限[17]。

图7 滑块导轨系统谐响应应力和位移分析
5 结论
1) 为了降低横摇载荷对船用多功能数控机床正常运行过程的影响,本文根据舰船波浪载荷下的摇荡特点,提出了机床在舰船环境下工作时应该保持关键运动副Z2运动方向与波浪横摇力方向垂直的布局方案,并针对机床关键导轨运动副进行了结构极限受载情况下的静态及谐响应动态稳定性分析。静态校核分析表明:机床关键导轨运动副的运行过程安全系数为26,结构稳定性较好;并且机床在最大的负荷下工作时,可以运行的寿命周期为169 013.76 h,为机床性能评估提供了理论依据。关键导轨运动副的波浪载荷谐响应动态分析结果表明:滑块导轨运动副最大应力与位移远小于机床滑块导轨结构的额定数值,进一步说明横摇运动不会对机床滑块导轨结构强度造成明显的影响。
2) 本文滑块导轨结构稳定性分析是基于稳态波浪载荷下舰船设备的正常工况分析,采用的理论分析方法具备通用性,能够对舰船设备的结构设计和分析提供一定的借鉴。但是,舰船设备极端环境下的波浪瞬态冲击强度分析以及波浪载荷与机床切削载荷的耦合分析尚待进一步研究。
参考文献:
[1] 徐滨士.徐滨士院士教学、科研文选[M].北京:化学工业出版社,2010:354-360.
[2] Li Y, Lin M. Regular and Irregular Wave Impacts on Floating Body [J]. Ocean Engineering, 2012, 42:93-101.
[3] Daniele D. Slamming Clustering on Fast Ships: From Impact Dynamics to Global Response Analysis [J]. Ocean Engineering, 2013, 62:110-122.
[4] 李积德.船舶耐波性[M].哈尔滨:哈尔滨工程大学出版社,2007:34-65.
[5] 黄武刚.船舶在波浪中航行时稳定性研究及其危险性分析[D].大连:大连理工学院,2010.
[6] 盛振邦,刘应中. 船舶原理[M].上海:上海交通大学出版社,2004:73-92.
[7] 邵开文, 马运义.舰船技术与设计概论[M].北京:国防工业出版社,2005:43-51.
[8] 戴仰山,沈进威,宋竞正.船舶波浪载荷[M]. 北京:国防工业出版社,2007: 16-28.
[9] 胡开业.船舶在波浪中的大幅横摇运动及其运动稳定性研究[D].哈尔滨:哈尔滨工程大学,2010.
[10] Junker J J. Stochastic Procedures for Extreme Wave Load Predictions-wave Bending Moment in Ships [J]. Marine Structures, 2009, 22:194-198.
[11] 中国船级社.钢质海船入级与建造规范[M]. 北京:人民交通出版社,2004:55-72.
[12] 中国船级社. 国内航行海船建造规范[M].北京:人民交通出版社, 2006:98-122.
[13] 中国船级社. 钢质海船入级与建造规范[M]. 北京:人民交通出版社, 2009:75-86.
[14] HIWIN集团天津龙创日盛机电实业有限公司.线性滑轨技术手册[Z]. 天津:HIWIN集团天津龙创日盛机电实业有限公司,2012.
[15] 刘称意. 考虑导轨结合面影响的数控机床动态特性分析及结构优化[D].沈阳:东北大学, 2010.
[16] Schellin T, Ostergaard C, Guedes S C. Uncertainty Assessment of Low Frequency Wave Induced Load Effects for Containerships [J]. Marine Structures, 1996, 9:313-332.
[17] 诸乃雄.机床动态设计原理与应用[M].上海:同济大学出版社,1987:63-78.
