非定常运动下的激波／边界层干扰分离特性研究

赵云飞，刘 伟，刘 绪，邓小刚

（国防科技大学 航天科学与工程学院，湖南 长沙 410073）

0 引 言

在超声速和高超声速飞行中，激波与边界层相互作用、相互影响的现象十分常见。这种干扰不仅产生气动加热，而且对机体的控制和发动机进气状态也有影响。因此，在高速飞行器开发、设计时，要保持飞行器飞行的高效率、高可靠性就必须深入了解飞行器流场的结构和特性。

最早注意到激波／边界层干扰现象是在20世纪30年代末，Ferri［1］在超声速风洞试验中，发现在机翼后缘附近激波与边界层干扰后产生了边界层分离现象。随后，包括美国、苏联（俄罗斯）、英国、德国等一些最早发展航空航天的国家相继开展了对这种干扰现象的研究。几十年来，人们通过大量的地面风洞试验、飞行试验、理论分析及计算研究，对激波与边界层干扰现象的复杂性及其对飞行稳定性及控制的影响已 经 有 了 非 常 深 刻 的 认 识 和 理 解［2－9］，Dolling［4］、Knight［5－6］以及 Zheltovodov［7］等的综述文献对这些研究工作做了较全面的总结。

要指出的是，目前国内外研究主要是集中在飞行器姿态不变假定下的激波／边界层干扰特性研究（包括由定姿态下非定常分离、脉动引起的非定常激波／边界层干扰）。然而，高速飞行器对于飞行条件的变化是非常敏感的，存在诸如机动动作引起的、大攻角舵效耦合引起的时延非线性、非定常动态特性问题。另外，诸多随机干扰因素对飞行器的飞行状态有着非常大的影响，对典型的高超声速飞行器布局而言，长周期模态是欠阻尼的（或不稳定的），短周期模态是不稳定的。这都使得飞行器处于非定常运动状态中。目前对于飞行器非定常运动状态下的非定常激波／非定常边界层干扰问题研究，由于受地面实验技术等因素的限制，缺乏深入了解，这对于确定干扰流场在多大范围内影响空气动力及气动加热环境，确定干扰域内的气动力载荷及气动热载荷，为工程设计提供最严重的临界设计条件还存在不足。因此，在上述研究工作基础上，进一步开展飞行器非定常运动状态下的非定常激波／边界层干扰特性研究是有重要意义的。

本文以二维压缩拐角这一经典的激波／边界层干扰问题为研究对象，采用五阶精度加权紧致非线性格式（WCNS）和非定常“双时间步”格式数值求解非定常雷诺平均N－S方程模拟压缩拐角在等速抬头、等速低头和周期性俯仰振动等不同运动方式下的非定常激波／边界层干扰现象，分析非定常激波／边界层干扰引起的分离流区非定常变化特性，并考察角速度、振幅和频率等参数的影响。

1 数值方法

1.1 流动控制方程和离散方法

流动控制方程为一般曲线坐标系下的非定常雷诺平均N－S方程：

式中Q ＝J－1（ρ，ρu，ρv，ρw，ρe）T是守恒变量，F、G、H和Fv、Gv、Hv分别是无粘通量和粘性通量。湍流模型采用一方程SA模型。

控制方程时间方向采用隐式非定常“双时间步”格式求解，时间导数的离散精度为二阶。空间项采用五阶精度加权紧致非线性格式WCNS［10］离散。该格式采用六阶单元中心型差分格式离散无粘导数项，以ξ方向为例：

1.2 压缩拐角运动方程

压缩拐角的运动方式包括等速抬头、等速低头和周期性俯仰振动，通过让模型绕定轴做单自由度旋转的方式实现。等速抬头和等速低头的运动方程为：

式中θ是俯仰角，θm是角振幅，k是无量纲减缩频率。在本文的坐标系定义中，压缩拐角低头时俯仰角θ为正号，抬头时俯仰角θ为负号，俯仰运动的轴心设在拐角点处。

压缩拐角运动过程中，网格与物体刚性固联，网格运动满足几何守恒律（∂J－1／∂t≡0）。初场采用定常问题的收敛解。壁面速度满足粘性无滑移条件V＝Vwall，内点速度Vi和虚拟边界速度Vg满足切向无滑移、法向无穿透的条件Vg＝2Vwall－Vi。

2 压缩拐角定姿态风洞实验模拟

通过模拟Settles等［11－14］的压缩拐角定姿态风洞实验，对所采用的五阶WCNS格式进行验证。表1是实验条件，包括8°、16°、20°三个压缩拐角，来流马赫数2.85左右，来流边界层为湍流态。实验结果表明：8°压缩拐角未发生流动分离，16°压缩拐角产生了微弱分离，20°压缩拐角形成了较大范围的流动分离。表中δ、δ＊和θ是在压缩拐角上游50.8mm位置处（即表1中的xupstream位置，该处边界层尚未进入分离区）测量的边界层厚度、位移厚度和动量厚度。数值计算时，为了保证来流边界层的状态与实验一致，本文采用文献［15－16］的做法，通过调整上游平板长度使边界层发展到xupstream位置处时动量厚度θ与表1给出的实验值一致。表2是按照这种方法确定的平板长度，同时给出了各边界层厚度与实验［13］和文献［16］采用SA模型计算结果的对比，整体上符合较好。

表1 压缩拐角实验条件和来流边界层参数［13］Table1 Freestream and inflow boundary layer data for compression ramp cases［13］

表2 来流边界层参数的对比Table2 Inflow matching results

图1是压缩拐角计算网格，以20°情况为例，坐标原点位于拐角点处，如前所述拐角前面很长一段平板用来发展来流边界层。网格数量为256×131（流向×法向），物面网格距离为1×10－6m，可保证无量纲壁面距离y＋＜1。

图1 20°压缩拐角计算网格Fig.1 Grid of 20°compression corner

图2是压缩拐角分离区阴影图与实验［11］的比较。8°压缩拐角情况下，激波紧贴物面，流动没有分离；16°压缩拐角存在微弱分离；20°压缩拐角形成了较大范围的流动分离，有明显的分离激波出现。计算结果与实验在激波的形状、位置和流动分离现象等方面与实验基本吻合。

图3是压缩拐角表面压力（以来流压力无量纲）与实验结果［13］的定量对比。8°和16°压缩拐角情况下计算结果与实验符合的较好；20°压缩拐角情况下，分离区内数值计算的压力比实验值偏高（根据Knight［6］的综述文献，这是RANS湍流模型在模拟强干扰、大分离激波／边界层干扰问题时普遍存在的问题），而在后面恢复段与实验一致。以上对比验证情况说明本文采用五阶WCNS格式模拟的压缩拐角激波／边界层干扰结果整体上是合理的。

图2 压缩拐角分离区阴影图的比较（上：实验结果［11］，下：本文计算结果）Fig.2 Comparison of shadowgraghs of compression corner with experiment（up：experiment［11］；down：present）

图3 压缩拐角表面压力分布与实验结果的对比Fig.3 Surface pressure distribution of the 8°，16°and 20°compression corner

3 动姿态压缩拐角计算结果

3.1 计算网格

本节以20°压缩拐角为模型研究其在等速抬头、等速低头和周期性俯仰振动等运动方式下的非定常激波／边界层干扰问题，自由来流条件与表1相同，来流马赫数2.85。与图1定姿态情况的计算网格相比，姿态运动情况下对压缩拐角计算网格做了以下调整（如图4）：

（1）为了更好模拟压缩拐角俯仰运动时平板前缘的非定常绕流情况，采用10°楔面补充了平板下方的计算区域，并在楔前缘采用采用很小的球头钝化（球头直径与平板长度的比值约为1／10000，测试情况表明这种钝化处理不影响计算结果的准确性）。

（2）由于压缩拐角运动时分离区大小会产生非定常变化，因此在分离区附近流向方向上进行了更宽范围的加密。网格总数为流向503×法向151。

3.2 等速抬头、等速低头运动

让20°压缩拐角按照方程（3）做等速抬头和等速低头运动，无量纲角速度取ω＝±0.001745，正号代表低头即逆时针旋转，负号代表抬头即顺时针旋转，旋转的轴心位于拐角处。初始时刻模型的俯仰角为零，以定常收敛解作为零时刻的初场。

图4 姿态运动情况下的压缩拐角计算网格Fig.4 Grid of compression corner for a movement condition

图5和图6分别是压缩拐角等速抬头和等速低头运动时的流场情况，从上到下包括5个不同的角位置，抬头：θ＝（0°，－4°，－8°，－12°，－16°），低头：θ＝（0°，4°，8°，12°，16°）。可以看出压缩拐角俯仰运动时，分离点、再附点和分离激波等都处于非定常运动中，且分离区的大小变化具有明显规律：等速抬头运动时分离区减小，等速低头运动时分离区增大。

模型运动引起分离区大小变化的原因可从两方面考虑：一是模型运动时姿态角发生了变化（引起了流动条件的变化），二是壁面运动速度等非定常效应的影响。为此将压缩拐角分别固定在θ＝±（0°，4°，8°，12°，16°）这些位置上不动，在同样的来流条件下做定常计算，进行对比分析。本文分离区大小的定义方法如图7，其中Δs代表分离点到拐角的距离，Δr代表再附点到拐角的距离（分离点和再附点根据表面摩阻系数Cf＝0确定），以Δs与Δr的和作为分离区的大小Δ，即Δ＝Δs＋Δr。分离区大小Δ随俯仰角θ的变化曲线如图8和图9。

图5 压缩拐角等速抬头过程中5个不同角位置上的流场情况，θ＝（0°，－4°，－8°，－12°，－16°）Fig.5 Flow of compression corner at five pitching angles during the pitching up course，θ＝（0°，－4°，－8°，－12°，－16°）

图6 压缩拐角等速低头过程中5个不同角位置上的流场情况，θ＝（0°，4°，8°，12°，16°）Fig.6 Flow of compression corner at five pitching angles during the pitching down course，θ＝（0°，4°，8°，12°，16°）

图7 压缩拐角分离区大小的定义方式Fig.7 The definition of separation size

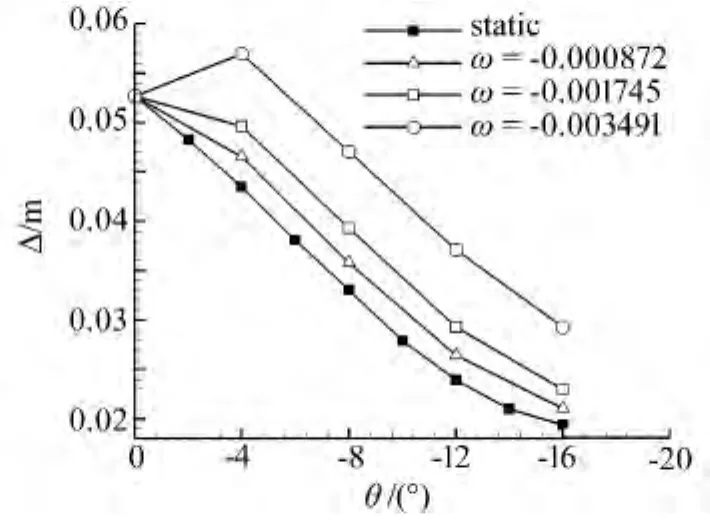
图8 静止不动与抬头运动的压缩拐角分离区大小对比Fig.8 Comparison of separation size between static and pitching up compression corner

图9 静止不动与低头运动的压缩拐角分离区大小对比Fig.9 Comparison of separation size between static and pitching down compression corner

对于等速抬头运动的情况，如图8，static是将压缩拐角固定在各角位置上不动时的定常计算结果，这时不存在壁面运动效应的影响，分离区大小的变化完全是由于姿态角的不同造成的，俯仰角（绝对值）越大分离区越小，这与图5压缩拐角运动时分离区大小随俯仰角的变化趋势相同，说明压缩拐角运动时姿态角的变化是影响分离区大小变化的主要因素之一。从图8中也可以看出，与静止不动的情况相比，压缩拐角等 速 抬 头 运 动 时 （ω ＝ －0.000872、－0.001745、－0.003491）分离区减小的相对更慢，说明非定常迟滞作用的影响减缓了分离区的变化。随着角速度减小曲线向静止不动时的曲线收敛。

对图9等速低头的情况进行类似的分析后得到的结论是：压缩拐角低头运动时俯仰角的增大使分离区增大；受非定常迟滞作用的影响，低头运动时分离区的增大速度也比静止不动时慢。

下面考察不同姿态角对分离区大小的影响。注意到在图5（a）和图6（a）的流场整体马赫数云图中，压缩拐角抬头或低头运动时来流在楔的上表面发生了膨胀或压缩，这样对于拐角区的流动来说其来流边界层的马赫数相应发生了变化。因此考虑上述姿态角不同引起压缩拐角分离区大小变化也可能是由于姿态角变化后引起来流马赫数的变化而造成的。为此，在其他来流条件不变的情况下，将模型的俯仰角固定在θ＝0°，只改变来流马赫数，单方面考察来流马赫数对压缩拐角分离区大小的影响。表3是5个来流马赫数条件，分别按照压缩拐角在俯仰角为8°、4°、0°、－4°和－8°时的波后马赫数取值，以便参考。图10是分离区大小随马赫数的变化关系，当马赫数增大时压缩拐角的分离区减小。因此可以将压缩拐角运动时引起来流马赫数变化对分离区大小的影响机制归纳为：

抬头角度增大→来流在楔的上表面发生膨胀→马赫数增大→分离区减小；

低头角度增大→来流在楔的上表面发生压缩→马赫数减小→分离区增大。

表3 来流马赫数的取值情况Table3 Value of freestream Mach number

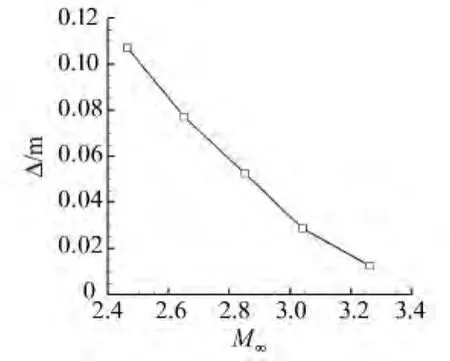
图10 压缩拐角分离区大小随马赫数的变化曲线Fig.10 Variation of separation size with Mach number

3.3 周期性俯仰振动

令压缩拐角按照方程（4）做周期性俯仰振动，振幅取θm＝4°，无量纲减缩频率k＝0.0314，对应的振动周期为T＝200。

图11是前3.5个振动周期内俯仰角、分离点Δs和再附点Δr随时间的非定常变化过程。压缩拐角做周期性俯仰振动时，分离点和再附点与俯仰角同样形成了周期性变化，而且频率相同。由于非定常迟滞作用的影响，分离点和再附点的相位比俯仰角落后约3π／10。图12是一个振动周期内8个不同相位角上（φ＝0，π／4，π／2，3π／4，π，5π／4，3π／2，7π／4）分离区的非定常流动情况。整体上模型下俯的过程中分离区变大，模型上仰的过程中分离区变小，这与前面等速抬头和等速低头运动得到的结论相符。

图11 压缩拐角周期性俯仰振动过程中俯仰角、分离点和再附点随时间的变化过程Fig.11 Variation of pitching angle，separation point and reattachment point during the forced oscillation

图13是分离区大小Δ随俯仰角θ的变化曲线，可以看出周期性振动情况下曲线具有明显的迟滞环特征。与图中模型固定在各角位置上不动时的定常计算结果（static）相比，周期性俯仰振动时（periodical oscillation）分离区的大小尽管整体趋势上仍然是模型下俯（down）的过程中分离区增大、上仰（up）的过程中分离区减小，但Δ的最大值和最小值并不是刚好出现在最大俯仰角（θ＝4°）和最小俯仰角（θ＝－4°）位置上，而是滞后了一些。根据图11，这个相位差大约是3π／10。

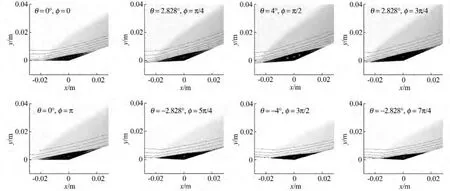
图12 压缩拐角一个俯仰振动周期内8个不同相位角上的分离区流动情况Fig.12 Flow of separation region in 8phases during aperiod of pitching oscillation

图13 周期性振动情况下分离区大小随俯仰角的变化曲线Fig.13 Variation of separation size with pitching angle

考察周期性俯仰振动的振幅θm对分离区大小和相位的影响，令方程（4）中减缩频率k＝0.0314不变，角振幅分别取θm＝2°、4°、8°和12°。图14是不同角振幅下分离区大小Δ随俯仰角θ的变化曲线。可以看出振幅的改变对曲线相位基本没有影响，但是对分离区的大小变化影响很大。振幅增大时，Δ的最大值变得更大，同时最小值也变得更小，也就是说分离区整体的变化范围变得更宽。

另外考察振动频率k的影响，令运动方程（4）中角振幅θm＝4°不变，无量纲减缩频率分别取k＝0.0157、0.0314、0.0628和0.1256。图15是不同频率下分离区大小Δ随俯仰角θ的变化曲线。不同频率下分离区大小的最大值和最小值差异不大，但不同频率的曲线间的相位差异十分明显。在低频率下（k＝0.0157），模型的运动速度较小，非定常迟滞效应相对较弱，与模型静止不动时（static）的情况类似，最大和最小分离区分别出现在最大和最小俯仰角上；当振动频率增大一些后（k＝0.0314），模型的运动速度加快，迟滞效应增强，流场的变化开始落后于模型的运动，所以最大分离区和最小分离区没有出现在最大俯仰角和最小俯仰角上，而是滞后了一些；当振动频率进一步增大后（k＝0.0628、0.1256），迟滞效应增强，曲线间的相位差越来越大，最大、最小分离区的角位置甚至与模型不动时完全颠倒。可见振动频率的改变对分离区大小的相位变化影响很大。

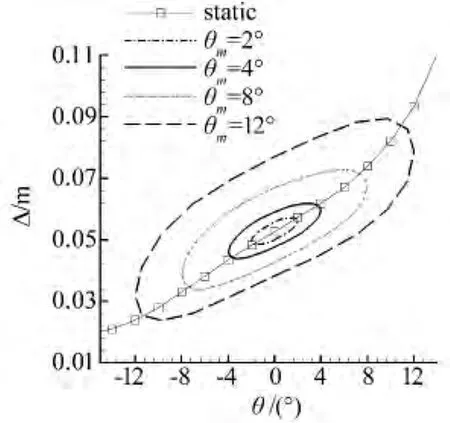
图14 振幅θm对分离区大小的影响Fig.14 Effect of amplitude on separation zone

图15 振动频率k对分离区大小的影响Fig.15 Effect of frequency on separation zone

4 结 论

本文采用五阶精度WCNS格式和非定常“双时间步”格式数值求解非定常雷诺平均N－S方程研究了二维压缩拐角模型在姿态运动情况下的非定常激波／边界层干扰问题，主要结论如下：

（1）压缩拐角等速抬头运动时分离区减小，等速低头运动时分离区增大；周期性俯仰振动时分离点和再附点的位置以及分离区的大小形成与模型同频率的周期性变化。

（2）通过与相同来流条件下定姿态计算结果进行对比分析表明，压缩拐角运动时模型姿态角的变化（引起了流动条件的变化）是导致分离区大小变化的主要因素，而模型运动的非定常迟滞作用会使这种变化减慢。

（3）模型姿态角的改变引起来流马赫数发生变化，从而对分离区大小产生了较大影响，其规律是：压缩拐角抬头（低头）→气流发生膨胀（压缩）→来流马赫数增大（减小）→分离区减小（增大）。

（4）周期性俯仰振动的振幅增大后，分离区大小的变化范围明显扩大，对相位影响不大；振动频率的改变对分离区大小的变化范围影响不大，但对分离区大小变化的相位的影响十分明显。

［1］FERRI A.Experimental results with airfoils tested in the high speed tunnel at Guidonia［R］.NACA TM－946，1940.

［2］LI S X.The complex flow dominated by shock wave and boundary layer［M］.Beijing：Science Press，2007.（in Chinese）李素循.激波与边界层主导的复杂流动［M］.北京：科学出版社，2007.

［3］ZHANG H J，MA H Y，TONG B G.Turbulence modeling validation in hypersonic complex flows［J］.ACTA Aerodynamica Sinica，2001，19（2）：210－216.（in Chinese）张红杰，马晖扬，童秉纲.高超声速复杂流动中湍流模式应用的评估［J］.空气动力学学报，2001，19（2）：210－216.

［4］DOLLING D S.Fifty years of shock－wave／boundary－layer interaction research：What next？［J］.AIAA Journal，2001，39（8）：1517－1531.

［5］KNIGHT D，JOSE L，DIMITRIS D，et al.Assessment of CFD capability for prediction of hypersonic shock interactions［J］.Progress in Aerospace Sciences，2012，48－49：8－26.

［6］KNIGHT D，HONG Y，ARGYRIS G P，et al.Advances in CFD prediction of shockwave turbulent boundary layer interactions［J］.Progress in Aerospace Sciences，2003，39（2－3）：121－184.

［7］ZHELTOVODOV A.Some advances in research of shock wave turbulent boundary layer interactions［R］.AIAA 2006－496.

［8］JACK R E.Numerical simulations of shock／boundary layer interactions using time dependent modeling techniques：a survey of recent results［J］.Progress in Aerospace Sciences，2008，44（6）：447－465.

［9］WU Y，YI S H，CHEN Z，et al.Experimental investigations on structures of supersonic laminar／turbulent flow over a compression ramp［J］.Acta Phys.Sin.，2013，62（18）：1－12.（in Chinese）武宇，易仕和，陈植，等.超声速层流／湍流压缩拐角流动结构的实验研究［J］.物理学报，2013，62（18）：1－12.

［10］DENG X G，ZHANG H X.Developing high－order weighted compact nonlinear schemes［J］.Journal of Computational Physics，2000，165：22－44.

［11］SETTLES G S，FITZPATRICK T J，BOGDONOFF S M.Detailed study of attached and separated compression corner flowfields in high reynolds number supersonic flow［J］.AIAA Journal，1979，17（6）：579－585.

［12］SETTLES G S，DODSON L J.Hypersonic shock／boundarylayer interaction database［R］.NASA CR－177577，1991.

［13］SETTLES G S，DODSON L J.Hypersonic shock／boundarylayer interaction database：new and corrected data［R］.NASA CR－177638，1994.

［14］SMITS A J，MUCK K C.Experimental study of three shock wave／turbulent boundary layer interactions［J］.Journal of Fluid Mechanics，1987，130：291－314.

［15］ZHAO R，YAN C.Evaluation of engineering turbulence models for complex supersonic flows［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（2）：202－205.（in Chinese）赵瑞，阎超.超声速复杂流动中湍流模型的评估［J］.北京航空航天大学学报，2011，37（2）：202－205.

［16］OLIVER A B，LILLARD R P，BLAISDELL G A，et al.Validation of high－speed turbulent boundary layer and shock－boundary layer interaction computations with the overflow code［R］.AIAA Paper 2006－894.