基于小波变换与均值滤波的渐进成形力信号处理研究*

罗小燕 陈宗玉 朱成尧

(江西理工大学机电工程学院，江西 赣州 341000)

板材渐进成形工艺具有不需要模具、成形周期短、制造成本低等特点，因此它在板材塑性成形领域具有广泛应用前景［1］。成形力信号的获取及分析是研究渐进成形规律的重要内容，它与工艺参数及成形质量的关系密不可分。由于成形力检测是一个动态过程，信号在数据采集、转换、传输的过程中极易受到周围环境的干扰，使得采集的信号包含真实信号与噪声两部分，不利于渐进成形规律的分析。传统的去噪方法对于含混合噪声的非平稳信号去噪效果不太理想。

目前小波阈值去噪主要是针对高斯白噪声进行研究的，而成形力信号中还混合着如脉冲噪声、机械噪声等其他噪声，因此仅仅利用小波阈值去噪方法对这些混合噪声的滤除效果不佳［2-3］。针对这种情况，本文提出一种将防脉冲干扰平均滤波与小波阈值去噪相结合的处理混合噪声的新方法。

1 小波阈值去噪原理

假设数据长度为N 的成形力真实信号被污染，其信号模型可表示为:

式中:Xn为含噪数据，fn为成形力信号;σ 为en方差，en为噪声。

小波阈值去噪原理是用信号与噪声在小波变换各尺度下不同的特性，将含噪信号进行多层小波分解，保留分解出来的低频系数，对高频系数采用阈值将其进行阈值化处理，低于阈值的系数将变成零，高于阈值的系数将保留或进行缩小处理。最后将得到的小波系数进行重构，这样就使信噪分离，得到去噪后的信号。

2 基于小波变换与均值滤波相结合的去噪方法

小波变换具有很好的时频局部分析能力以及多分辨率特性，而且对白噪声具有很好的去噪效果。防脉冲干扰平均滤波算法，也称去极值平均滤波算法，是结合算术平均与中值算法形成的，该算法对随机干扰以及脉冲干扰等滤除效果较好，并且可以适当减小噪声误差，便于信噪分离。因此将这两种方法相结合用来处理成形力信号不仅可以很好地去除混合噪声，而且可以深入分析信号成分及特征。成形力信号结合法去噪的步骤及实现方法如下:

(1)将成形力原始信号进行去极值平均滤波处理

去极值平均滤波处理是对连续N 次的采样数据f(xi)进行大小排队，去除队列中的最大值和最小值，然后对剩下的数据求平均作为本次采样的输出值。这样通过平均滤波后的噪声信号方差小，更有利于后续小波去噪。取N=5 时，则有

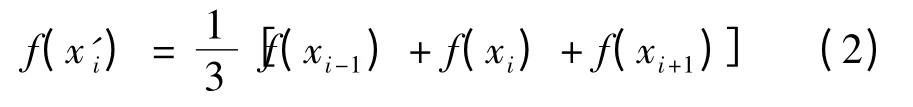
以白噪声n(t)为例，其服从N(0，σ2)分布，并且E［n(u)n(v)］=σ2δ(u -v)，式中，

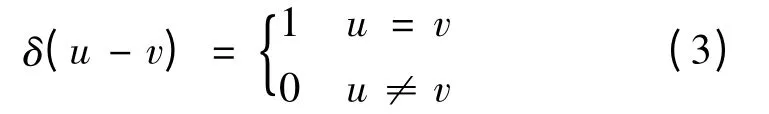
因此，方差

由此可见，白噪声的方差减小了些，有利于后续的小波去噪。

(2)将预处理的信号进行小波分解

选择合适的小波函数以及小波分解尺度，然后对成形力信号进行小波分解。

(3)对小波各尺度分解的系数进行阈值量化处理

选择阈值规则后，根据规则进行小波阈值处理，并通过软阈值去噪。

(4)成形力信号细节重构

对处理后的小波系数进行重构，得到成形力信号细节信号特征。

为了比较去噪效果，除了观测去噪后的信号图，本文还综合信噪比(SNR)、均方根误差(RMSE)，以及平滑度(r)指标进行去噪评价。

SNR、RMSE、r 的定义分别如下［4］:

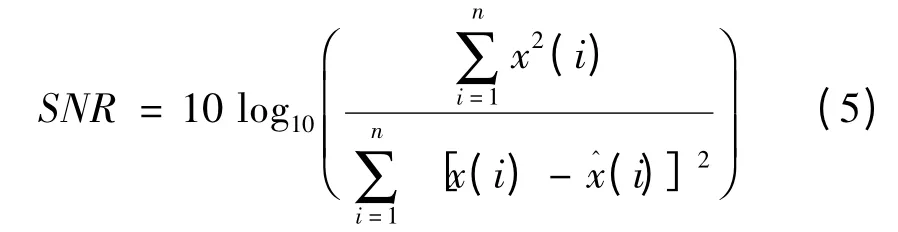
3 去噪方法中几个关键参数的选取

3.1 小波函数及分解尺度的选取

(1)小波函数的选取

根据成形力信号特点要求选用的小波函数应具有以下特性:

①可进行离散小波变换。考虑到成形时间较长，成形力的采集数据量大，在小波变换时具有较快的分析速度。

②具有消失矩。保证准确获取成形力信号中的奇异点特征。

③具有对称性。关系到成形力信号重构后的信号失真问题。

根据以上给定要求，结合目前常用的小波函数可知，可选用的小波函数有Symlets 小波系、Daubechies小波系以及Coiflet 小波系。

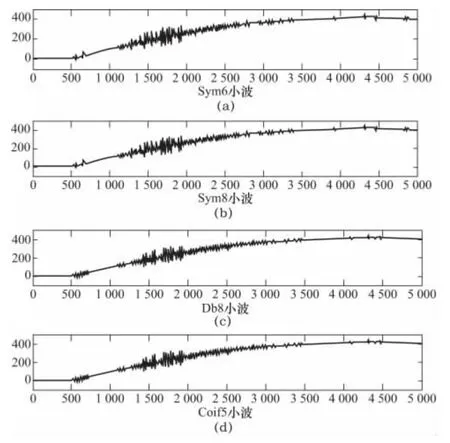
图1 不同小波去噪效果图

下面以成形力原始信号为研究对象，采集数据点数为5 000，小波函数分别取Sym6、Sym8、Db8、Coif5，选择Birge-Massart 算法获取阈值，进行5 尺度小波分解去噪。去噪效果图如图1 所示，去噪效果评价指标值如表1 所示。

表1 不同小波函数的去噪指标值

(2)小波分解尺度选取

小波分解尺度对小波去噪效果有着很大的影响，在小波分析中，分解尺度J 一般取3～5［5］。分解尺度越大，信号与噪声分离就越彻底，但计算量大，并且在重构信号时失真也大。分解尺度小，信号与噪声就不能完全分离，影响信号的分析与研究。因此必须选择一个合适的分解尺度进行信号去噪。

下面选用db8 小波函数，分解尺度分别取3～5 进行成形力信号去噪。去噪效果图如图2 所示。

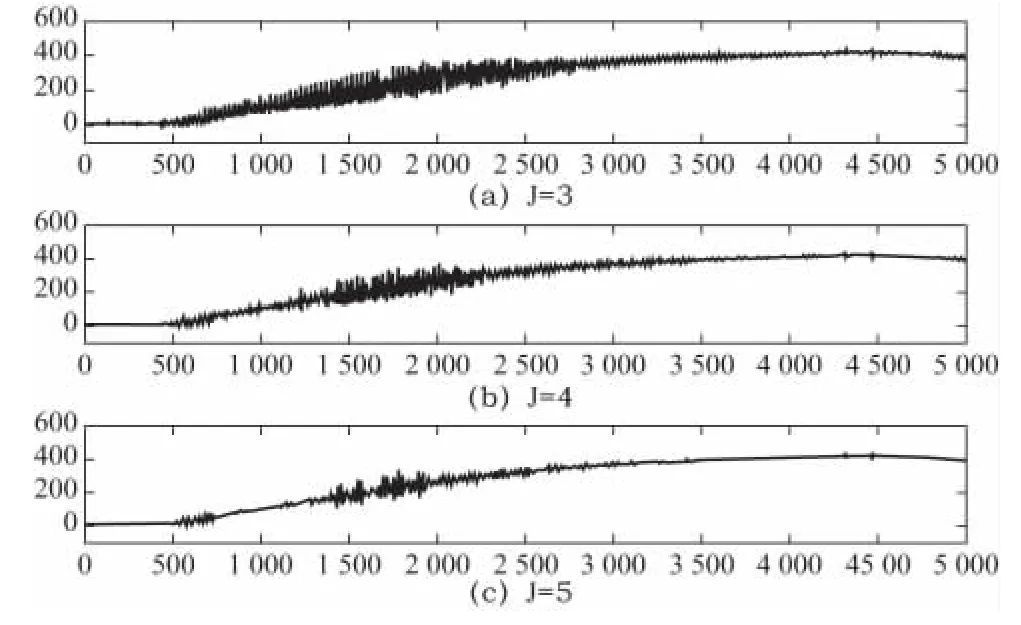
图2 不同分解尺度下的成形力信号去噪效果图

不同小波尺度的去噪指标值如表2 所示，表中给出了信号的信噪比、均方根误差以及平滑度值。

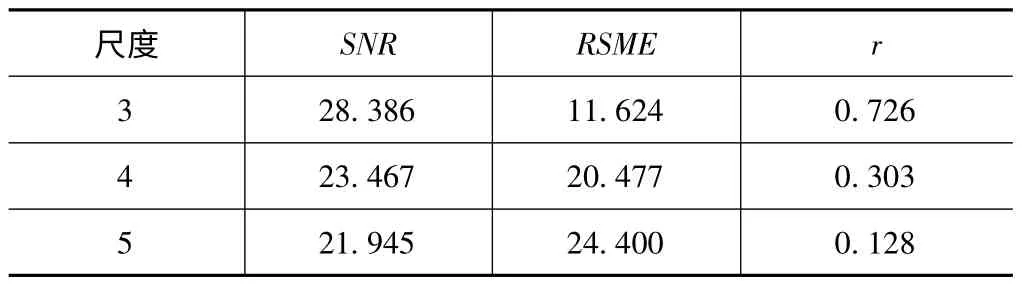
表2 不同小波分解尺度的去噪指标值

从图2 可以看出，不同的小波分解尺度对信号去噪效果有着明显影响。在尺度5 的去噪效果相对尺度

3、4 较好。

从表2 可以看出，尺度为3 和4 的信噪比相对尺度5 要大，均方根误差相对较小，但从图2 的去噪效果图看出，尺度为3 和4 时去噪效果并非理想的。因此单独看这两个评价指标是不可靠的，需结合起来分析。从表2中可以看出，尺度5 的平滑值更小，去噪曲线更光滑些，而且仍然保留了信号的细节。因此尺度5 去噪效果更佳。

3.2 阈值及阈值函数的选取

(1)阈值选取

目前小波阈值去噪常用的阈值选择主要有以下4种［6］:①选择rigrsure 阈值规则;②采取固定值的sqtwolog 阈值去噪;③选择heursure 阈值去噪;④通过极大极小准则选择阈值。

不同的阈值对去噪的效果是不一样的。下面以成形力信号为研究对象，采样数据个数为5 000，其他参数不变，分别采用以上4 种阈值进行自动去噪，其去噪效果对比图如图3 所示(截取一段曲线分析)。相应的去噪评价指标如表3 所示。

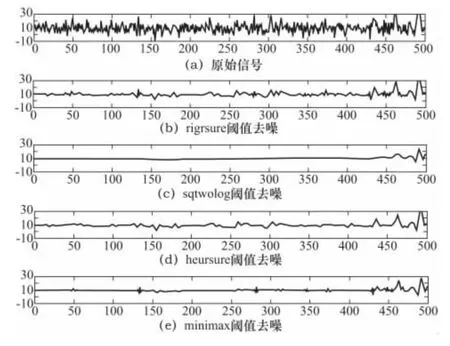
图3 4 种阈值去噪效果对比图

结合图3 与表3 可知，rigrsure 和heursure 两种阈值去噪的信噪比另两种高，均方根误差较小，说明这两种阈值规则下的去噪效果较好。从图3、表3 中还可以得知基heursure 阈值的去噪信号曲线较光滑，但是也对信号的一些细节造成损失，而rigrsure 阈值的去噪情况较理想，基本保留了信号的细节特征。因此本文最终确定选用rigrsure 阈值进行去噪。

表3 4 种阈值去噪评价指标值

(2)阈值函数选取

小波分解得到小波系数后，对其进行阈值量化。目前对阈值处理应用比较广泛的方法有两种，分别为硬阈值函数和软阈值函数。

①硬阈值函数

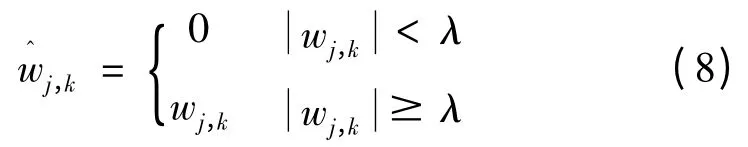
②软阈值函数

从阈值函数的数学表达式可以看出，硬阀值函数实质上简单地对小波系数进行处理，即小于阈值的小波系数置于零，大于等于阈值的保持不变。而软阈值处理的不同之处在于大于等于阈值的小波系数返回值是它们之间的差值。软阈值去噪效果明显。由于硬阀值函数在阈值处不连续，在信号重构时会出现一些震荡。因此，它不如软阈值去噪信号光滑，硬阈值去噪相对较粗糙些。本文成形力信号处理选用软阈值函数。

4 实验结果与分析

为了验证新的去噪算法的有效性，下面以成形力原始信号为例，选用db8 小波函数进行去噪，分别与默认阈值去噪、去极值平均滤波进行比较分析，去噪效果如图4 所示。

图4 不同方法去噪效果

从图4 中不难看出，去极值平均滤波对原始信号变化不大，去噪效果不是很好，而小波阈值去噪可以去除大部分噪声，但是仍然有些噪声未得到很好地抑制，利用去极值平均滤波和小波变换相结合的去噪效果要优于前两种，这也说明这种结合去噪方法的可行。同时表4 给出了小波变换与结合法去噪的去噪指标值。

表4 不同方法去噪的评价指标值

从表4 中也可以看出，基于均值滤波与小波变换相结合的去噪信噪比比单纯用小波变换的要略大些，并且均方根误差略小些。因此，将这种方法应用在成形力信号处理效果要好些。

5 结语

本文针对含混合噪声的信号去噪问题，提出了基于小波变换与均值滤波相结合的新去噪方法。并以渐进成形力信号为研究对象，讨论并确定了小波阈值去噪的几个重要参数。通过实验对比，表明基于小波变换与均值滤波相结合的新去噪方法比小波阈值去噪效果更佳。同时也说明，小波变换与其它传统的滤波方法相结合，能取得较好的去噪效果。

［1］周六如.板料数控渐进成形中变形力的研究［J］.精密成形工程，2010(1):10 -14.

［2］马琳伟，莫健华.基于有限元仿真的金属板材单点渐进成形分析［J］.塑性工程学报，2007(6):96 -100.

［3］Amino H，Lu Y，Maki T.etal.Dieless NC forming prototype of automotive service parts［C］.Proceeding of 2nd International conference on Rapid Prototyping and Manufacturing，2002:179 -185.

［4］文鸿雁.基于小波理论的变形分析模型研究［D］.武汉:武汉大学，2004.

［5］王芳.小波分析在信号去噪中的应用研究［D］.成都:西华大学，2009.

［6］王秉仁，杨艳霞.小波阈值降噪技术在振动信号处理中的应用［J］.噪声与振动控制，2008，12(6):9 -12.

［7］陶珂，朱建军.小波去噪质量评价方法的对比研究［J］.大地测量与地球动力学，2012，32(2):128 -133.

［8］谢文涓，蔡改贫，姜志宏.小波变换技术在圆度误差检测中的应用［J］.工具技术，2009，43(6):102 -104.