活用教材，搭建思维的桥梁

朱艳

根据新课标的理念，教师与学生共同参与的课堂，应该是一个学生主动建构的过程，也是基于数学教材、教师、学生三方互动吸收的过程。在这个过程中，教师的身份就是紧扣教学主线，为学生的思维搭桥，连接教材和学生的“学习”，构建灵活的课堂探究模式。那么如何为学生成功搭建思维桥梁呢？

一、抓住教材线索，重建教学模式，激发学习动力

由于学生年龄小，缺乏数学经验，认知和接受数学知识的能力存在着个体差异，教师要在教学中从学生心理出发，针对学习材料的组织和使用，对教材进行重新建构，激发学生对数学学习的动力。

“平行四边形的面积”的教学是在活动探究的基础上，先进行动手操作而后验证，让学生感受转化思想，最终实现问题的分析和解决。教材给出的是以学生猜想花坛面积和数方格的办法，让学生开展探究过程的。我在使用的过程中发现，大多数学生将不太容易将数方格法和面积之间建立直观概念，为此我进行了如下设计。

让学生将准备好的教具（四根6cm和2根4cm的木条）拿出来制作一个平行四边形，并同学之间进行比较，看看各自做的平行四边形有何异同。而后我也展示了自己做的几个平行四边形，如图1。

师：我这里的平行四边形也是用4根6cm和2根4cm的木条围成的。看看有什么异同？它们的面积相等吗？

学生根据已有的知识和经验，立刻展开了猜想：

生1：相等。因为用的小棒是一样多的。

生2：不相等。因为形状是不一样的。

生3：我觉得相等也有可能，但不相等也有可能。

与教材的设计相比，显然这种问题的引入方式对学生更具有诱惑力，也能够为学生的进一步探究做足准备，提供保障。

二、遵循教材规律，优化探究过程，发展学生思维

小学生的认知思维遵循一个从直观感知——建立表象——抽象概括的发展过程，具有从直观到抽象的渐进发展规律。因此，小学数学活动必须要从学生的认知水平和认知经验入手，建立合理的探究过程。

“平行四边形的面积”的教学重点和难点，是让学生在面积公式的推导过程中，发展数学思维。教材编排的探究过程是以动手操作为基础，让学生将平行四边形转变为一个长方形，通过剪、切、割、补的方法，进而推导出两种图形的关系得出面积公式。如何让学生对动手操作这个环节不但知其然，而且知其所以然呢？

我先让学生对平行四边形的面积进行猜想，学生提出有两种可能： 1.平行四边形的面积=底×高； 2.底边×邻边；然后让学生将之前准备的学具（长方形和平行四边形的纸片），将这两者重叠起来进行比对。

师：思考两个面积哪个大哪个小？

生1：感觉长方形要大一些。

师：凭感觉是不准确的。需要动手操作验证。想想看，怎么操作？

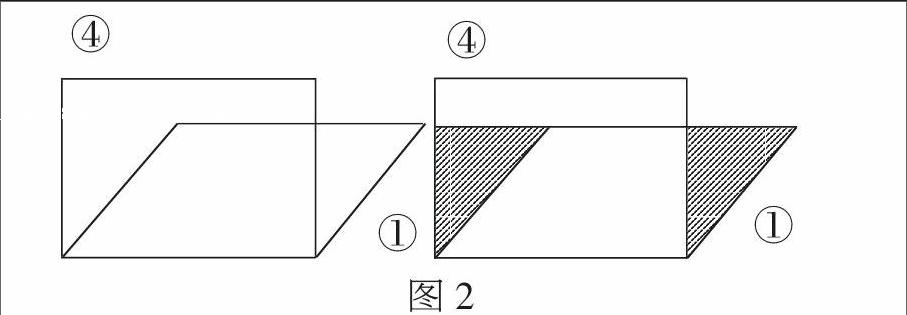
将长方形和平行四边形的重合过程进行动态演示（如图2）。

由此学生看到，可以将平行四边形右边多出的部分，剪下拼接到左边，这样就形成了一个长6cm、宽4cm的长方形。

师：拼成长方形后有什么变化？为什么小了呢？

通过对教材的准确把握和重新解读，学生在层层探究中进一步丰富了数学表象，建立了平行四边形的面积计算方法，在此基础上引导学生类推，抽象出计算公式就水到渠成了。

三、挖掘教材内涵，渗透思想方法，提高数学素养

数学的灵魂，是开启世界的思想方法。在教学中，教师不但要挖掘教材内涵，向学生提供知识，更要创设积极的探索情境，使学生的思维投入到积极的探究过程。

“平行四边形的面积”学习中观察、猜测和验证的过程，其中运用到的转化就是一个重要的基本数学思想方法。根据教材安排，学生在进行转化推导时是从数方格的方式引入。而针对长方形和平行四边形的大小问题，显然让学生进行独立转化是有难度的。为此我进行了如下设计。

我选取了图2的①④图形，让学生思考：如何进行剪拼才能进行比较？然后让学生根据重叠演示，观察并思考长方形和平行四边形之间的变化。

学生在转化思想的推动下，获得了分析问题和解决问题能力的培养，强化了转化思维的内因，能够运用数学思想方法来解决问题。

总之，教材是学生学习的依据，是教师组织教学的武器。唯有用活教材，读透教材，才能用数学知识给学生打开一个思维的空间，使其建构宏伟的数学思想大厦，从而发展数学能力，提高数学素养，这其中最重要的，要归功于教师在教材和学生之间搭建的这座思维的桥。

（责编 金 铃）endprint