经验:除了提取,还需要存储
2014-04-04陈雨华
陈雨华

教学过程:
一、创设情境,感受“比”的意义
1. 直接揭示课题
师:今天,我们来学习“生活中的比”。先给同学们介绍一位21世纪最杰出的帅哥,有图为证。(先出示老师自己一张标准尺寸的照片,学生大笑,然后逐张出示按照不同比例变化后的照片)
师:观察这些照片,你有什么发现?(生答略)
2. 研究照片长与宽之间的关系
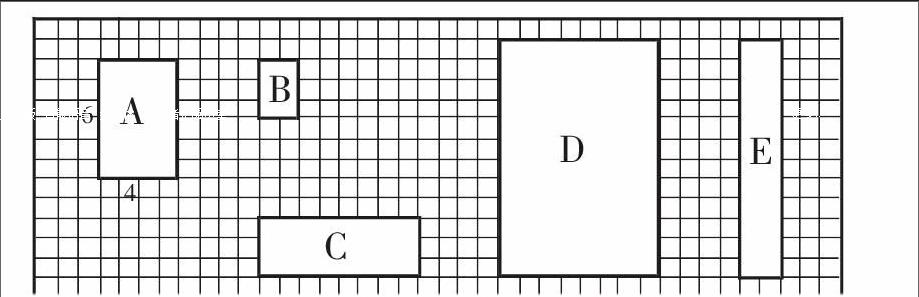
师:为了便于研究,我们把这些照片都放到方格纸中。(点击课件,隐去照片,出示长方形长与宽的数据,如下图)
师:请同学们仔细观察一下,这些长方形的长和宽之间有什么关系?把你的发现在小组内交流讨论。
生1:长方形A的长和宽分别是B的2倍,面积是B的4倍。
师:对。也就是说,从A到B,长和宽分别——(缩小2倍)那你再观察一下长方形A和D,它们之间是怎样的关系?
生2:长方形A的长和宽分别是D的二分之一。
师:下面我们再看一下,对于长方形A,它的长和宽之间有什么关系呢?
生3:长是宽的1.5倍。
师:你是怎么得出这个结论的?其他几个长方形的长和宽的关系,谁能说一下?
生4:长方形A、B、D的长都是宽的1.5倍,而长方形C、E不是。
3.讲解“比”
师:学到现在,有的同学可能会问“老师,你让我们学比,比在哪呢”,你们能从黑板上找到“比”吗?
生(少数):长方形A的长与宽的比是3︰2。
师:你能凭借自己的经验说说对这个3︰2的认识吗?(学生讨论,师相应板书“两个数相除,又叫这两个数的比”,然后引导学生自学课本P50的内容)
师:通过自学,你学到了哪些知识?什么是比?比的各部分名称是什么?同桌说一说。
师:根据比的意义,任何两个数相除都可以写成比的形式。
师板书:6÷4= 6 ︰ 4 =1.5
| | | |
前 比 后 比
项 号 项 值
……
[思考:将课本中“淘气”的图片改成老师自己的照片,这一学习素材的呈现使学生感到亲切、自然,既拉近了师生间的距离,又使课堂气氛变得轻松、活跃。通过师生、生生之间的相互交流,让学生深刻感受到同一照片长与宽之间的比、不同照片长与长之间的比,使“比”这一概念在学生头脑中留下深深的烙印,体验到数学学习的乐趣,获得了大量的数学活动经验。]
二、深化对“比”的认识
1.在数学日记中找“比”
出示小明的数学日记:10月1日,我们一家驱车2小时来到了80千米外的农家乐。中午用餐时,爸爸要了3瓶啤酒花了15元,我点了两盒花生牛奶花了20元。我发现这种花生牛奶的口感非常好,其实它是用花生浆和甜牛奶配成的,其中花生浆占10%。
师:你们能从中找到比吗?比一比,看谁找到的比多。(有些学生无从下手,师提示只有找到除法关系就可以改写成比了)
生5:我找到80比2。
师:你说的80是指什么,2又是指什么呢?比值是什么?(生答略)
师(小结):路程和时间的比值实际上就是速度。
生6:15比3。
师:能说明一下你说的比吗?
生6:我说的是啤酒的总价与啤酒瓶数的比,它的比值实际上就是啤酒的单价。
生7:我找到一个比是2比3,是花生牛奶盒数与啤酒瓶数的比。
生8:我找到一个比是10比100。因为花生浆占花生牛奶的10%,所以这个10%是用花生浆除以花生牛奶得到的。
师:你真了不起,看到了隐藏中的比。其实,花生浆占花生牛奶的10%就是指花生浆与花生牛奶的比是10比100。以前学百分数时,教材上有这么一句话(大屏幕出示):像95% 、 100 % 、 65.8 % ……这样表示一个数是另一个数的百分之几的数叫做百分数。百分数也叫百分率或百分比。对于“百分数也叫百分率”同学们都已经理解了,但是对于百分数为什么叫百分比,许多同学当时都不理解,现在你们明白了吗?(生答略)
师:对了,百分数实际上就是一个数与另一个数的比。其实,10%中还隐藏着许多的比,你们能找出来吗?
生9:甜牛奶与花生牛奶的比是90比100。
生10:花生浆与甜牛奶的比是10比90。
……
[思考:通过小明的数学日记,给学生提供大量的生活学习素材,让学生在头脑中对这些素材进行“再加工”,提取出各种各样有关比的信息。这里面,既有同类量之间的比,如啤酒瓶数与花生牛奶盒数之间的比,又有不同类量之间的比,如路程与时间的比、总价与数量的比等。通过这样的教学,使学生对“比”有了更全面、更深刻的理解。特别是通过对“其中花生浆占10%”这个信息的深入剖析,既沟通了新旧知识之间的联系,帮助学生更轻松地理解“比”的本质内涵,又使学生对百分数的理解上升到了一个新的高度。]
2.寻找身边的“比”
师:今天我们学习比,那我们眼睛看上去就到处都是比,你们能说说吗?
生11:我找到一个比是26︰25,因为我们班有26名男生和25名女生。
生12:我发现一个比是1︰51。
师:你们能猜出他说的比是谁与谁的比吗?
生(齐答):是老师与同学的比。
生13:我找到一个比是2︰3,因为我的文具盒里有两枝铅笔和三支中性笔。
……
3.介绍身体上的“比”
师(大屏幕同时出示):其实,我们的身上也有许多比。如两手平伸的长度和自己身高的比约是1︰1,人的心脏与拳头的比约是1︰1,成年男子的肩宽与头长的比约是2︰1,一个人的血液与体重的比大约是1︰13,婴儿的头长与身高的比是1︰4……(师边介绍,学生边比划,并让学生说说各个比的具体含义,最后定格在婴儿的头长与身高的比例图上)endprint
师:谁能说说这个1︰4的具体意义?
生14:如果把婴儿的头长看成1份的话,那么婴儿的整个身高就有这样的4份。
师(请一位学生上台):你们观察一下,这位同学的头长与身高的比是1︰4吗?
师:再请同学们仔细观察一下,老师的头长与身高的比大约是多少?
师(小结):同样是头长与身高的比,婴儿的大约是1︰4,儿童的大约是1︰6,成人的大约是1︰7。另外,有些成人的头长与身高的比是1︰9,这种人很适合做一种工作,你们能猜出来吗?(大屏幕出示模特的图片)
……
[思考:学生从自己的身边找到了大量的比,感受到了比在生活中的广泛应用,积累了研究问题的一般方法,即可以从广度与深度两个方面去研究问题。最后着重理解“头长与身高的比”,使学生认识到人的不同阶段头长与身高的比是在不断变化的,而处在同一阶段的不同的人的头长与身高的比大体上是一致的,但也有特例,使学生初步感受到事物是普遍联系的,同时又是处在不断发展变化之中的。]
三、拓展对“比”的认识
1.联系比较
师:同学们,今天我们认识了比,实际上比就是表示两个数相除的关系,因此比和除法可以说是孪生兄弟。那么,比和除法之间到底有什么样的关系呢?(生答略)
师:除此之外,你还会想到比和谁有着密切的联系呢?
相机板书:
2.展开讨论
师:想一想,你认为比的后项有什么特殊要求吗?
生:比的后项不能为0。
师(质疑):体育比赛中的2︰0是怎么回事呢?
师(小结):体育比赛中的比分,其实跟我们课前提到的比多比少、比大比小一样,都是差比关系,而我们今天学习的“生活中的比”是特指两个量之间的倍比关系。
四、全课总结(略)
……
思考:
1.经验除了提取,还需要存储
提到“比”,学生肯定不陌生,但学生经验中的“比”更多的是指向于比多比少、比大比小的“差比”,或者说在他们头脑中“差比”与“倍比”是不加以明确区分的。当然,从课堂中学生多次提到“比例”一词的情况,说明学生对“比”还是有一定经验积累的。所以,教学中我们应尽量去调取关于“倍比”的经验,克服经验系统中“差比”带来的负面影响。课堂中我通过多媒体隐去照片,将其变成一个个长方形并置于格子图中,让学生直接来研究这些长方形长与宽的关系。这个环节花费了不少的教学时间,但我认为在这个环节的时间使用上还是很值得的,因为在这个环节中不仅引出了今天的学习内容“比”,更重要的是为学生对“比”的认识奠定了鲜活的生活基础,同时为后续“比的应用”“图形的缩放”“比例尺”“正比例和反比例”等知识的学习积累了宝贵的经验。
2.提供综合性材料,拓宽学生探索的空间
教材上一共提供了三个情境来引出“比”,在磨课过程中我发现单独出示每个情境总有点突兀,而且情境之间缺少联系,导致学生获得的信息是单一的、有限的。于是我思考将教材的后两个情境糅合在一起,但后来又想“比”在生活中的应用是极其广泛的,教材既然强调从生活中去寻找“比”,我为什么不可以创设一个更为宽广的生活情境,让学生从中去探寻更多的“比”呢?最后我采用了数学日记,将众多的信息一并呈现,让学生自己去加工处理,发现各种类型的比。另外,同类量之间的比和不同类量之间的比的综合出现,虽然课堂中我没有刻意去加以区分,但相信通过这样的教学,学生对比有更全面、更深刻的理解,同时减少了教学环节,使课堂结构显得更为严谨。更为重要的是,在这一过程中,学生获得了大量的对于“比”的体验,积累了选择信息、分析信息、处理信息的经验。
(责编 杜 华)endprint
