关于复正规矩阵的2个不等式

沈 浮，夏必腊，周堂春

(解放军陆军军官学院数学教研室，安徽 合肥230031)

0 引言

矩阵不等式是矩阵理论中的一个很重要内容。随着矩阵理论的迅速发展及其在自然科学、工程技术和社会经济等领域的广泛运用，关于矩阵不等式的新结果层出不穷。文献［1］中的定理3.9指出:当A是Hermite矩阵时，则有λmin(A)E≤A≤λmax(A)E。文献［2］中定理6.2.2又指出:当A和B为2个非负定的Hermite矩阵时，则有0≤trAB≤λmax(A)trB≤rtA·trB。这2个结果都是针对Hermite矩阵的，本文对复正规矩阵进行了研究，得出了更进一步的结论。

本文中，用Re(z)表示复数z的实部，用λmin(A)和λmax(A)分别表示Hermite矩阵A的最小特征值和最大特征值，用λRmin(A)和λRmax(A)分别表示复矩阵A实部最小的特征值和实部最大的特征值，用tr(A)记矩阵A的迹，向量x的共轭转置用xH，E表示n阶单位矩阵。

1 基本概念及相关引理

定义1:设A∈Cn×n，若对任意非零列向量x∈Cn×1，都有

则称A为复正定矩阵(或复非负定矩阵)，记作A＞0(或A≥0)。

显然，当A为Hermite正定(非负定)矩阵时，它也是复正定(非负定)矩阵。

定义2:设A、B∈Cn×n，如果A－B是复正定矩阵(或复非负定矩阵)，则称复矩阵A大于复矩阵B(或称复矩阵A大于或等于复矩阵B)，记作A＞B(或A≥B)。

本文要用到复正定(非负定)矩阵以下几个重要结果，把它们作为引理1。

引理1［1］:(1)设A=(aij)n×n∈Cn×n，且A是复正定矩阵(或复非负定矩阵)，则Re(aii)＞0 (或Re(aii)≥0)(i=1，2，…，n)。

(2)A是复正定(非负定)矩阵的充要条件是:A+AH为Hermite正定(非负定)矩阵。

(3)复对角矩阵A=diag(λ1，λ2，…，λn)是复正定(非负定)矩阵的充要条件是:Re(λi)＞0 (Re(λi)≥0)，i=1，2，…，n。

(4)设A、B∈Cn×n，若A＞B，P为n×m的列满秩矩阵，则PHAP＞PHBP;当P不是列满秩时，由A≥B只能推出PHAP≥PHBP。

定义3:如果方阵A∈Cn×n满足AAH=AHA，则称A为正规矩阵。

引理2［3］:A∈Cn×n，则A酉相似于对角矩阵的充分必要条件是:A为正规矩阵。

引理3［4］:设A∈Cn×n是正规矩阵，则A为复正定(非负定)当且仅当A的特征值实部皆为正(非负)。

引理4［5］:设A、B∈Cn×n都是正规矩阵，则A、B可同时酉对角化的充要条件是AB=BA。

2 主要结果

下面的定理1、定理2及其推论就是本文的主要结果。

定理1:设A∈Cn×n是正规矩阵，则λRmin(A) E≤A≤λRmax(A)E。

证明:A是正规矩阵，由引理2知，存在酉矩阵U，使A=Udiag(λ1，λ2，…，λn)UH，这里λ1，λ2，…，λn必是A的n个特征值。于是由引理1的(3)、(4)知

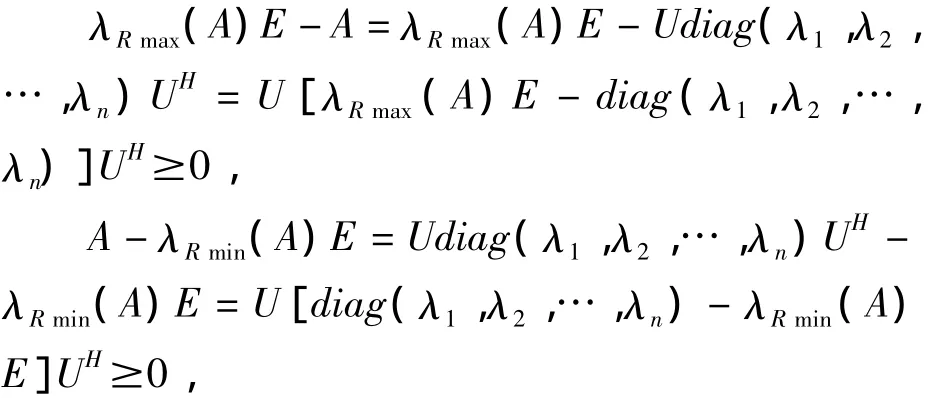
即λRmin(A)E≤A≤λRmax(A)E。

由于复正定(非负定)的正规矩阵特征值实部全为正(非负)，所以由定理1便得如下推论。

推论:设A∈Cn×n是复正定(非负定)的正规矩阵，则

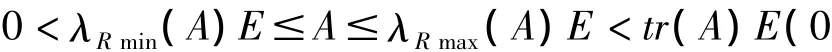
定理2:设A、B∈Cn×n是复正规矩阵，AB= BA，A、B的特征值分别为λ1，λ2，…，λn和μ1，μ2，…，μn，则当Re(λRmin(A)μj)≤Re(λjμj)≤Re (λRmax(A)μj)(j=1，2，…，n)时，Re(λRmin(A) trB)≤Re(trAB)≤Re(λRmax(A)trB)。

证明:因A、B可交换的正规矩阵，由引理4知:A、B可以同时酉对角化，即存在酉矩阵U，使得A=Udiag(λ1，λ2，…，λn)UH，B=Udiag(μ1，μ2，…，μn)UH。于是有

即λRmax(A)B－AB酉相似于对角矩阵。由于Re (λjμj)≤Re(λRmax(A)μj)(j=1，2，…，n)，故对角矩阵的对角元的实部全非负，从而λRmax(A)B≥AB。类似可证:当Re(λRmin(A)μj)≤Re(λjμj)(j =1，2，…，n)时，λRmin(A)B≤AB。于是得

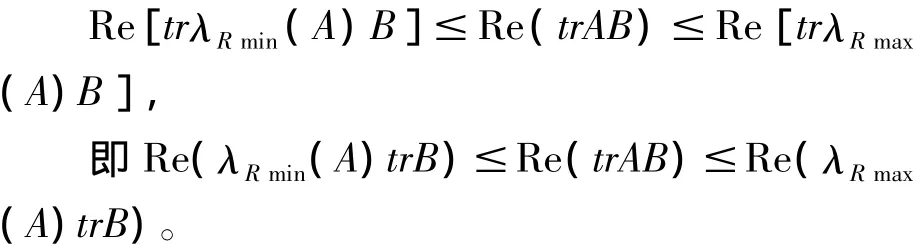
推论1:当A∈Cn×n是复正规矩阵，B∈Cn×n为非负定的Hermite矩阵时，AB=BA，Re(λRmin(A)) ·trB≤Re(trAB)≤Re(λRmax(A))·trB。

证明:设A、B的特征值分别为λ1，λ2，…，λn和μ1，μ2，…，μn，因B是非负定的Hermite矩阵，所以其特征值μi(i=1，2，…，n)非负，于是在定理2证明中出现的(λRmax(A)－λi)μi(i=1，2，…，n)实部全非负，从而λRmax(A)B≥AB，类似地可以证明:λRmin(A)B≤AB。故

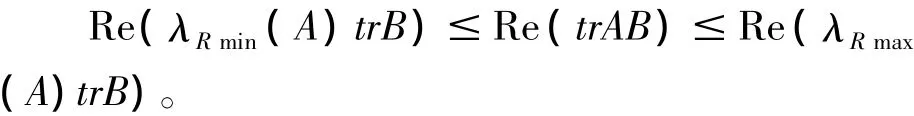
注意到trB≥0，便得Re(λRmin(A))·trB≤Re(λRmax(A))·trB。

推论2:设A∈Cn×n是非负定的正规矩阵，B∈Cn×n为非负定的Hermite矩阵，AB=BA，则0≤Re (λRmin(A))·trB≤Re(trAB)≤Re(λRmax(A))· trB。

证明:由推论1知，Re(λRmin(A))·trB≤Re (trAB)≤Re(λRmax(A))·trB显然成立。再由trB≥0及Re(λRmin(A))≥0，便可得出推论2。

推论3:设A∈Cn×n是非负定的Hermite矩阵，B∈Cn×n为非负定的正规矩阵，AB=BA，则 λmin(A)·Re(trB)≤Re(trAB)≤λmax(A)·Re(trB)。

证明:在定理2中，如果设

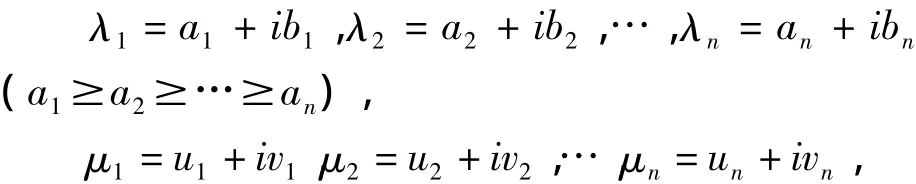
则定理2的条件Re(λRmin(A)μj)≤Re(λjμj)≤Re(λRmax(A)μj)(j=1，2，…，n)就变成

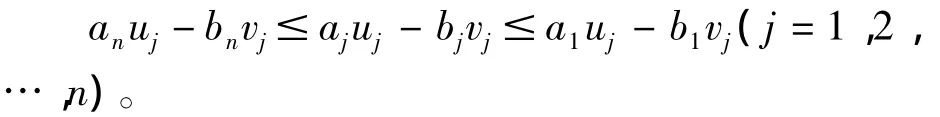
在本推论中，依条件及引理3知:所有的aj≥0，bj=0，uj≥0，(j=1，2，…，n)，所以条件

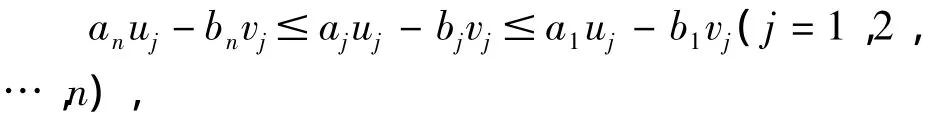
相当于

此不等式显然成立。于是由定理2得:

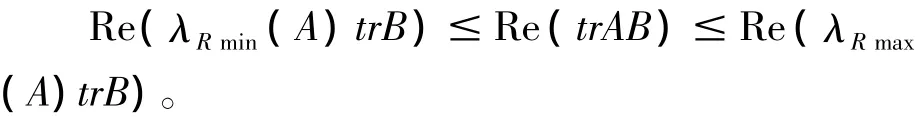
注意到A是非负定的Hermite矩阵，即λRmin(A)=λmin(A)，λRmax(A)=λmax(A)，便得

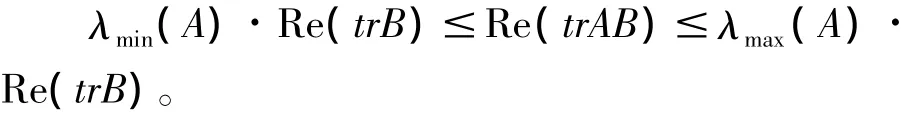
［1］ 方宝镕，周继东，李医民.矩阵论［M］.北京:清华大学出版社，2004:110－116.

［2］ 王松桂，吴密霞，贾忠贞.矩阵论不等式(第二版)［M］.北京:科学出版社，2006:129－131.

［3］ 程云鹏，张凯院，徐 仲.矩阵论(第3版)［M］.西安:西北工业大学出版社，2006:100－106.

［4］ 袁晖坪.关于复矩阵乘积的正定性［J］.数学的实践与认识，2006，36(11):202－206.

［5］ 史荣昌，魏 丰.矩阵分析(第3版)［M］.北京:北京理工大学出版社，2010:115－125.

［6］ 詹兴致.矩阵论［M］.北京:高等教育出版社，2008: 39－45.

［7］ 金 能.关于复正定矩阵乘积迹的估计［J］.工科数学，2002，18(4):106－108.