主成分分析在GPS噪声剔除中的应用分析

刘慕溪

(广东省核工业地质局测绘院，广东 广州510800)

0 引言

随着卫星、导航定位技术的发展，空间定位测量技术(尤其是GPS测量)在测绘中应用越来越广泛;GNSS系统，如美国的GPS、俄罗斯的GLONASS和北斗卫星导航系统，都能为用户提供海量的数据信息［1］。全球已建成上百个全球连续运行参考站和数千个区域站，不但可以观测到地表位移，进行形变分析以及板块运动研究，而且还能观测到震后形变等微小地壳形变，为地壳研究提供基本的原始资料。但测量不可避免的存在误差，GPS测量中的误差主要体现在与卫星有关的误差，与接收机有关的误差，与信号传播有关的误差，如何剔除GPS观测值中的误差，降低噪声对观测成果的影响成为一个重要问题。对流层湿延迟、电离层延迟、天线相位中心误差和卫星轨道误差等都是噪声的潜在来源，随着算法和模型的改进，该类噪声能得到很好的消除或减弱。此外GPS观测值中包含着时空相关的噪声，以及非构造信号等共性误差，对观测结果带来不确定性［2］。本文讨论了基于主成分分析的噪声剔除方法，结果表明主成分分析法可以较好地消除GPS解中的共性误差，提高GPS测量定位的精度。

1 主成分分析

1.1 主成分分析概述

主成分分析又叫经验正交函数分析，是现代数据分析的一个有效工具，广泛应用于经济、金融、测绘等领域，是一种非参数数据处理方法，计算简单、效率高［3］。主成分分析法在测量控制网的灵敏度分析、粗差检验等得到了较好应用。通过寻找观测数据的方差－协方差阵的前k个主分量，在保持数据信息损失最小的前提下，经过线性转换将原始自变量中相关的维数消除，转换到低维向量空间，低维中各主分量是相互正交的，从混杂的数据中提取出相关的信息。由于前几个主分量综合了原始数据的最大信息量，因此不会对数据分析结果带来太大的影响，同时避免了法方程病态问题的出现，得到参数的精确估值，提高了解的准确性和可靠性，同时可以揭示数据中隐含的一些规律及结构特征［4］。

1.2 主成分分析原理

观测P个变量x1，x2，…，xp，n个样本的数据资料数据矩阵为:

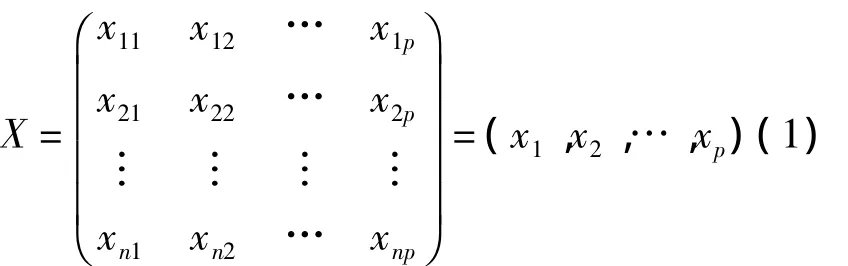
主成分分析就是将p个观测变量综合成为p个新的变量(综合变量)，即

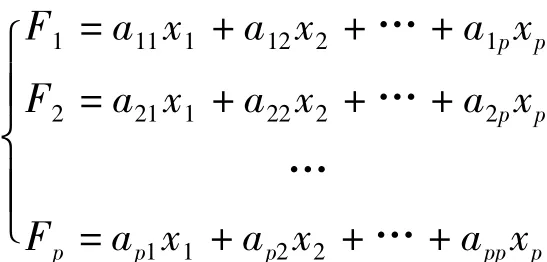
简写为:

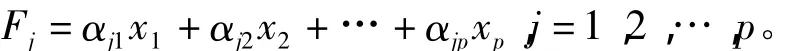
要求模型满足以下条件。

(1)各主分量不相关，即Fi，Fj互不相关(i≠j，i，j=1，2，…，p)。

(2)F1的方差大于F2的方差大于F3的方差，依次类推。

于是，称F1为第1主成分，F2为第2主成分，依此类推，有第p个主成分。主成分又叫主分量。这里aij称为主成分系数。通过前k个分量能够反应随机变量X的主要特征，该数据处理方法称之为主成分分析。

主成分分析法一般分3个步骤进行求解: (1)首先对分析数据组成数据矩阵X(m，n)，m为数据类型，n为数据样本个数;(2)数据中心化，即将各个观测数据减去均值得到新的数据矩阵; (3)计算新矩阵的方差、协方差，获取特征向量，实现在重构误差最小的条件下对数据维数的有效简化。

1.3 GPS噪声剔除中应用

以GPS台站网的坐标时间序列为原始数据，每个台站的坐标分量残差时间序列排列起来形成一个(m＞n)的矩阵X，m表示观测历元数，n表示观测类型，数据矩阵如下:

做如下定义:

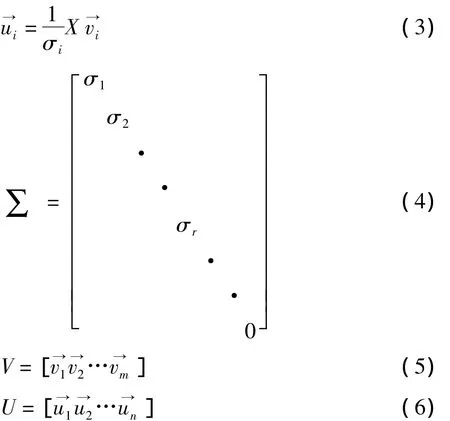
即V构成X的正交基底，矩阵X按照KLE展开可得

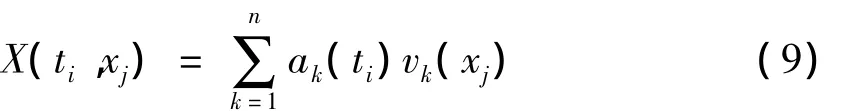
ak(ti)可由下式求出:

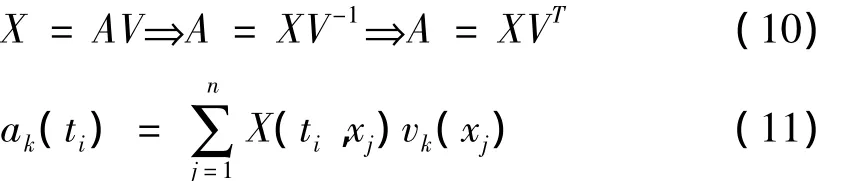
式中，ak(t)是第k个主成分，vk(x)是对应主成分的响应特征矩阵，分别代表时间特征和空间响应［5］。

2 实例分析

本文对连续运行的IGS基准站2001－2007的观测数据进行分析。首先对GPS观测数据进行预处理，GPS数据预处理是指及时对外业观测数据进行检验，探测数据中的粗差，剔除那些质量较差的数据，以提高观测数据的质量。在数据预处理的过程中，使用TEQC软件，对GPS数据进行质量分析［6］。数据预处理后按照如下步骤进行数据处理［7］。

(1)采用GAMIT软件，通过无基准方法解算出各GPS站点的三维坐标及其方差－协方差阵，以每天24 h的GPS观测数据为基本单位形成单天解。无基准算法可以有效地避免基准误差的干扰，便于将内部独立的坐标基准转换到外部统一的参考框架。

(2)将获取的单天解进行平差，获得单天解坐标序列。对坐标序列去均值和趋势项处理后(此处减去均值是为后续应用主成分分析法进行噪声分析做准备)，得到GPS基准站单天解连续坐标时间序列，限于篇幅以CAND站为例，图1为CAND站垂向分量坐标序列。

(3)将上一步生成的残余坐标时间序列进行主成分分析，把时间序列分解成时间域的主分量和空间域的特征分量，按其贡献率排列，见表1。

表1 主成分分析后得到的前3个主分量的贡献值

由表1可知在3个坐标方向主成分分析后前3个分量的累计贡献率达到90%，综合了绝大部分的原始信息，故采用前3个分量作为主分量，对GPS单天解形成的连续坐标时间序列进行处理，得到站点单天解的残余序列(图2)。

图1 CAND垂向分量坐标序列

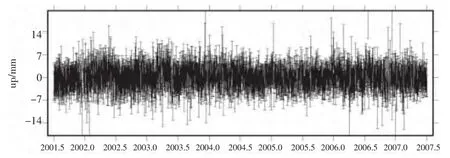
图2 经过主成分分析剔除噪声后的坐标序列

通过主成分分析法处理后，GPS单天解的坐标序列可看出，GPS坐标序列的波动趋于平稳，波动振幅有所减小，对非构造信号、时空相关的误差源引起的站点位移进行了剔除。对数据进行分析可知，滤波之前垂向分量的均方根误差为1.751 8，滤波之后为1.556 0，即通过主成分分析滤波方法分离出的误差约减少了站点11%的不确定度，提高了站点坐标的精度、信噪比。此外，滤波前坐标序列呈现出明显的周期性变化，滤波后坐标序列的周期性明显减弱，表明坐标序列中存在的误差呈现出季节性变化趋势，有待于进一步分析。

3 结论

本文基于主成分分析的噪声剔除方法，针对GPS信号中存在的非构造信号误差，时空相关误差等，能有效的剔除或减弱上述误差的影响，可提高GPS测量、定位的精度与可靠性，对GPS的应用具有一定的的参考价值。

［1］ 夏金伟，赵东保.TEQC数据质量分析［J］.地理空间信息，2012，(4):60－65.

［2］ 田云锋，沈正康.GPS坐标时间序列中非构造噪声的剔除方法研究进展［J］.地震学报，2009，(1):68－81，117.

［3］ Shlens J.A Tutorial on Principal Component Analysis，Center for Neural Science［J］.New York University New York City，NY 10003－6603 and Systems Neuro blogy Laboratory，Salk Insitute for Biological Studies La Jolla，CA 92037，April 22，2009.

［4］ 冯光财，陈正阳.基于主成分回归的GPS高程曲面拟合［J］.测绘科学，2007，32(1):51－52.

［5］ 殷海涛，甘卫军，熊永良，等.PCA空间滤波在高频GPS定位中的应用研究［J］.武汉大学学报(信息科学版)，2011，(7):825－829.

［6］ 贺小星，周世健.某城区D级GPS静态控制网设计与实施［J］.江西科学，2012，30(3):295－298.

［7］ 王 敏，张祖胜，许明元，等.2000国家GPS大地控制网的数据处理和精度评估［J］.地球物理学报，2005，(4):817－823.