改进的ANFIS在房产评估中的应用

史东辉

Shi Donghui

安徽建筑工业学院电子与信息工程学院 安徽 合肥 230088

School of Electronics and Information Engineering，Anhui University of Architecture，Hefei 230088，China

1.引言

房产价格评估非常重要，尤其对于税务部门[1][2]，正确的评估能够客观反映房产的价值。但房产的价格由许多因素决定，对房产进行评估有一定复杂性。房屋评估一般从三个方面来进行，建筑特征、区位特征、近邻特征。房产的建筑属性值可以通过房产交易数据库获得，区位特征和近邻特征，特别是近邻特征很难从交易数据库中获取相应信息, 房产近邻的准确定义是非常困难的[2]。一般是先对房屋近邻特征变量进行实地考察,根据评估人员经验来确定，由于涉及近邻特征信息众多，人为因素多，工作量大等原因，难以应用近邻特征准确地对房屋评估。传统的计算机房产价格评估方法多采用多元回归分析等，准确性有待进一步提高[2]。近年来，许多研究者开始将非传统方法应用于房产评估，并获得了一些成果，最主要的非传统方法是基于神经网络的方法[3][4][5],自适应神经模糊推理系统[6][7]（Adaptive Neuro-Fuzzy Inference System，ANFIS）等。本文将进一步研究ANFIS在房产评估的应用，研究地理位置，时间与房产价格的关系，通过定义房产近邻，即房产的k近邻，计算k近邻的房产平均价格，改进自适应神经模糊推理系统。

2.自适应神经模糊应用于房产评估现状

Hasiloglu,Yilmaz等(2004)，应用自适应神经模糊推理系统预测不稳定传热，发现 ANFIS比多元回归方法具有更好的效果[8]。Byme(1995),Bagnoli,Smith和Halbert(1998)最早将ANFIS应用于房产评估，研究表明ANFIS模型可以自动产生模糊规则和隶属函数, 获得房产各种属性与价格之间的复杂非线性关系[9][10]。

Guan,Zurada(2008)使用ANFIS用于房产评估[1]，采用美国中部区域1982到1992年房产销售数据，共363条记录，19个输入变量，作为实验研究对象。实验将输入数据随机分成训练集（40%，共142条记录），验证集（30%，共107条记录），和测试集（30%，共106条记录），实验仿真运行50次获得统计平均值。在ANFIS模型中，选择减法聚类，快速建立不同类别，用于ANFIS 初始模型的建立；使用混合学习算法将最小二乘法和梯度下降法相结合的学习算法进行前向传递和反向传递。选择原始数据集19个变量中相关的14变量作为所有变量数据集，使用R2方法、主成分法对数据集降维处理，获得另外两组对照数据集。用R2方法降维后获得11个输入变量；用主成分方法降维后获得4个主成分输入变量。与传统方法相比，使用所有变量作为输入变量时，平均错误率比传统方法稍差，对输入变量降维后，获得较少的输入变量，平均错误率好于传统方法，说明 ANFIS方法能对房产价格进行评估有一定的效果，值得更近一步研究。尽管ANFIS 对房产价格有一定的作用，但由于实验数据量较小，不能充分反映数据特性，另外数据集中没有地理位置信息，研究范围有很大的局限性，另外没有合理定义某一房产近邻,并采用近邻均价对房产价值进行预测，没有充分应用历史数据对房产进行的有效预测。

在后面的研究中，通过加入地理位置，研究地理位置对模型预测准确性的影响，以及房龄对房产价格评估的影响，并以此为基础，提出基于k近邻自适应神经模糊网路推理方法，进一步改进ANFIS模型的预测准确性。

3 基于k近邻自适应神经模糊推理系统

3.1 自适应神经模糊推理系统

研究采用的自适应神经模糊推理系统基于Sugeno计算模型的模糊推理系统[11][12]，将神经网络的自学习功能和模糊推理系统的模糊语言表达能力结合起来，通过系统自身的训练和学习过程，不断自动调整变量隶属函数参数，获得模糊推理系统输入、输出关系的最佳组合。图1为用于房产评估的ANFIS结构：

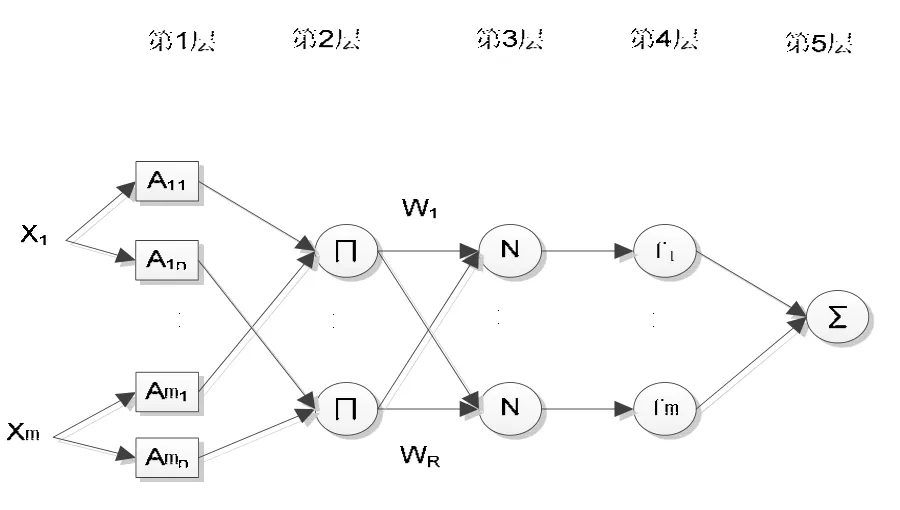
图1 房产评估ANFIS 结构图

第1层：将输入变量模糊化，输出为模糊集隶属度。Xi是输入，Aij是第 i个节点的隶属函数。这些参数是自适应的，函数的数值由0到1.随着参数的改变，随着函数数值改变，输入变量x的隶属程度改变。这一层，有m*n个节点，m输入变量的数量，n是隶属函数的数量。Oij为隶属度：

房产估价模型µij选择为高斯型隶属函数：

σ,c确定隶属函数图形。

第2层：实现条件部分的模糊集运算，计算每个规则的适用度：

Xi为输入变量。

第3层：将各条规则的适用度归一化。Wi是第i个规则适用度。通过规则适用度比所有规则适用度之和计算归一化规则适用度：

第4层：自适应层，每个节点都是线性函数，函数的系数通过最小二乘法和反向传播算法相结合的方法调节：

其中 fk是第k个模糊规则的输出。:

第5层：输出层，计算模糊推理系统的总输出，这一层得到前面层的输出之和：

前件参数和后件参数根据算法自动调节，获得输入输出的最佳组后。

3.2 K近邻

在房产评估中，通过某一房产周围房产的平均价格预测该房产的实际价格，不同的房产近邻的定义具有不同平均价格，但精确定义房产的近邻是非常困难的事，一般根据房产评估人员的经验，或根据行政区域划分来判定。研究表明使用单纯的区域划定获得的平均价格对房产价格的评估准确性的提高作用不大[2]。以下通过定义不同k近邻数据，解决房产近邻的准确定义问题。

定义1：已知多维数据为a1,……,aN，对应的域分别D1,……, DN，D为数据对象集，对每个数据对象t, t ∈D，t1属性值为t2属性值为,两数据对象距离定义为:

定义2：已知D为数据对象集，数据对象t, t的k近邻数据为t0,满足k-nearest(D,t0)，即t0,t1∈D, Distance(t,t0)<=Distance(t,t1); t1为k近邻以外数据对象。如k为1时，t0为最近邻数据。

定义3：计算最近邻时，多维数据a1,……,aN所有属性参与计算，同定义1, 称为全变量k近邻；选择部分属性参与计算，称为部分变量k近邻；

定义4：参与计算距离的数据对象t仅为数据对象中房产地理位置,对应属性x、y，t0∈D，其中t0, 满足k-nearest(D,t0),计算k近邻时仅考虑不同数据对象中地理位置的距离，称为房产的空间k近邻；

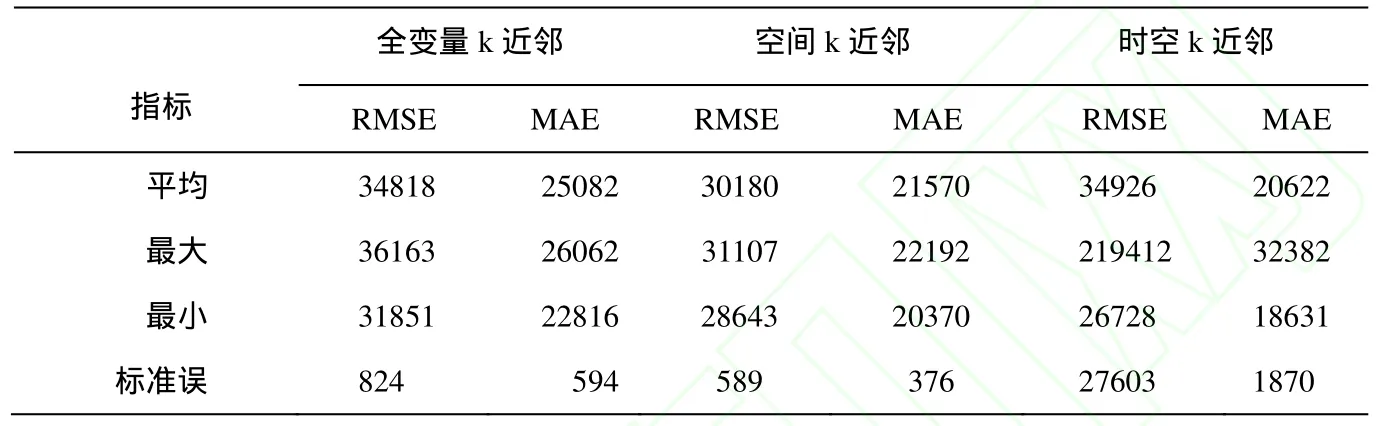
定义5：已知房龄a0，参与计算距离的数据对象t仅为数据对象中房产地理位置,对应属性x、y，t∈D1, 具有t的数据对象对应房龄a

3.3 kd-树最近邻搜索算法[13]

kd树是多维空间有效组织点集合而产生的一种空间分割数据结构。把多维空间分割成若干个不相交的子区域，空间中任何一个点属于某一子区域，建立kd树。

算法1

kd树搜素算法描述:

（1）首先通过二叉树搜索比较查询节点和分裂结点的分裂维的值。

（2）查找与待查点同一子空间的叶子结点。

（3）然后回溯搜索路径，并判断搜索路径上的结点的其他子结点空间是否可能有最近点，如果有，到此结点空间继续搜索。

（4）重复，直到搜索路径为空。

3.4 基于k近邻ANFIS算法

对房产的k近邻定义后，通过基于k近邻ANFIS算法，计算k近邻房产平均价格，将k近邻平均价格作为输入变量，产生ANFIS模型结构，求得最优的模糊推理的系统模型。以下算法2为基于k近邻ANFIS改进算法的描述。

算法2

基于k近邻ANFIS改进算法描述：

(1) 选择对房价影响较大相关属性用于计算距离；

(2) 查找数据集D中每个数据对象t的k近邻为t0，使得t0满足Distance(t,t0)<=Distance(t,t1)；根据k近邻的不同定义，可能是全变量k近邻，部分变量k近邻，空间k近邻，和时空k近邻；

(3) 查找k近邻对象t0所对应的房价y(t0)，并计算均价；

(5) 重复以上步骤，直到找到最优模型。

4.实验结果分析

4.1 实验数据描述与实验方法

实验使用Matlab Fuzzy Logic Toolbox，选取美国中部区域2003到2007年房产销售数据，共13892条记录，16个输入属性，其中包括两个地理位置属性x,y，一个房产价格属性作为输出属性。

考虑到通货膨胀，房产价格用以下公式调整：

148,548$为数据集中最后一年即2007年均价。

在ANFIS模型中，选择减法聚类，使用混合学习算法将最小二乘法和反向传播相结合的学习算法进行前向传递和反向传递。

房产评估误差结果的测量采用以下几种测量方法：

均方根误差（RMSE）是使用较多的一种方法，说明样本的离散程度，运算结果与预测结果具有同样单位，但其缺点是夸大了离群数据的作用，均方根误差计算公式：

平均绝对误差（MAE），结果与预测结果有同样单位，计算公式如下：

平均绝对百分比误差（MAPE），是绝对百分比误差的平均值，用于比较预测的准确性。平均绝对百分比误差计算公式：

以上公式中N为测试集数据对象个数。

4.2 将房产的经、纬度加入ANFIS模型

数据集没加入房产的地理位置信息数据集，简称所有变量（不含位置），共13892条记录，14个输入属性，一个房价输出变量；包含所有变量数据集，即加入房产地理位置信息，包括经度、维度，共16个输入变量，一个房价输出变量。将两个数据集分别用同样的方法将输入数据随机分成训练集（40%），验证集（30%，），和测试集（30%），实验仿真运行50次获得统计平均值。 计算得到RMSE,MAE及MAPE。在表1中，所有变量（不含位置）模型的平均MAPE为21.64%，所有变量（含位置）的平均MAPE为20.26%,有所改进。MAPE误差在小于等于的5%范围内，所有变量（含位置）的模型百分比为24.4%；大于所有变量（不含位置）的22.8%，说明模型准确性改善。从表2可以看出，所有变量（包含位置）的测试集的模型RMSE、MAE的数值分别为34423、24837，而所有变量（不包含位置）测试集模型的RMSE、MAE数值为36345，26610，有明显的改进，验证数据集有相同的结果。该实验表明，加入地理位置信息后，模型预测准确率提高，说明房产的价格与地理位置有较密切的关系，在房产价格评估中应充分考虑地理位置信息。

表1 所有变量（不含位置）和（含位置）测试集的MAPE

表2 所有变量（不含位置）和所有变量（含位置）模型测试集的RMSE和MAE

4.3 房龄对模型的影响

使用SAS软件计算房龄（房产的销售日期减房产的建立日期）的分布情况，发现房龄的分布是不均匀的，房龄的中值是33年，50 %房产房龄小于33年；90%的房产房龄小于67年；最大房龄为115年，只有10%的房产在67到115之间。因此将原始数据按房龄分成为房龄为0数据集；房龄为小于等于33数据集；房龄大于33并且小于67数据集；房龄大于67数据集。比较不同房龄模型的准确性。 表3中房龄小于0的数据集的对应模型平均MAPE为11.92，房龄小于等于33数据集的对应模型平均MAPE为11.74，房龄小于等于66，大于33数据集的对应模型平均MAPE为23.48，房龄>66数据集模型为35.5, 房龄小于0的数据集MAPE小于等于5%范围内，模型输出百分比为34.5%，房龄小于等于33数据集，平均MAPE也有较好效果为11.74%，远大于其他数据对应模型准确率。但由于房龄小于或等于0的数据集所包含的数据对象较少，表4中显示，RMSE,MAE分别为43495,26353大于其他数据集。表3中显示，房龄大于66数据集的平均MAPE数据为35.5%，在MAPE的5%范围,输出模型百分比只占12.8%，具有最小预测准确性，同时表4中模型输出RMSE和MAE误差值分别为43685,32476，同样说明房龄大于66时，有较大的预测误差。该实验表明房产的价格与房龄有密切关系，ANFIS模型对房龄较大的房产预测准确性下降。

表3 不同房龄模型测试集的MAPE

表4 不同房龄模型测试集的RMSE和MAE

4.4 将不同定义k 近邻房产加入ANFIS模型

由于房产与地理位置，时间等因素有较大关系，单纯通过将地理位置的经纬度加入模型不能完全表示地理位置对房产价格的影响。通过定义全变量k近邻，空间k近邻，时空k近邻，使用前述算法2，计算房产均价，将不同定义的k近邻均价加入ANFIS模型的输入变量。

表5，表6为k取值为10时，各种k近邻模型应用于测试集的误差对比结果。表5中全变量k近邻测试集MAPE为19.84%，大于所有变量（不含位置）的MAPE值21.64%，及所有变量（含位置）的测试集MAPE的值20.26%。表6中全变量k近邻测试集的RMSE值34428,MAE值24739，大于所有变量（不含位置）的RMSE的值36345,MAE的值26610。说明全变量k近邻房产均价对预测模型有一定改进。

通过测试集对模型进行测试，表5中可以看出全变量k近邻平均MAPE为19.84%,空间k近邻测试集上的平均MAPE为17.08%，时空k近邻为9.86%；MAPE的5%范围内，全变量k近邻模型输出百分比为22.4%,空间k近邻为28.4%，时空k近邻为42.4%。时空k近邻，空间k 近邻预测准确性有极大提高。表6中，由于时空k近邻选取记录较少，因此其预测误差RMSE值31770，,MAE值20788，稍大于空间k近邻,RMSE的值30114，MAE的值21330。

表7和表8为k取值为20时，各种k近邻模型应用于测试集的误差对比结果。表7中可以看出全变量k近邻平均MAPE为20.32%,空间k近邻测试集上的平均MAPE为17.24%，时空k近邻为9.56%，时空k近邻，空间k 近邻预测准确性有很大提高，表7与表5有相似的结果。表8中全变量k近邻测试集的RMSE及MAE值分别为34818,25082，空间k近邻分别为30180,21579，时空k近邻分别为34926,20622，均大于所有变量（不含位置）的RMSE的值36345,MAE的值26610，与表6有相似的结论，说明k近邻房产均价对预测模型有一定改进。表8中的全变量k近邻、空间k近邻、时空k近邻的RMSE,MAE值，除时空k近邻的MAE值为20622有所减少外，普遍有所增加。另外表8中时空k近邻的RMSE的最大值增大，标准误增大，说明k近邻的k值选取过大可能会引起误差增大，某些房产的近邻价格会影响房产的评估，降低房产预测的准确性。

表5 不同k近邻模型测试集的MAPE(k=10)

表6 不同k近邻模型测试集的RMSE和MAE(k=10)

表7 不同k近邻模型测试集的MAPE(k=20)

(10,15] 16.30 16.40 15.60(15,20] 11.20 10.90 7.30(20,25] 7.40 6.60 2.90>25 20.10 15.70 3.10

表8 不同k近邻模型测试集的RMSE和MAE(k=20)

5.结束语

本文首先将地理位置加入原始数据集，研究全变量（不含位置信息）与全变量（含位置信息）分别作为输入数据集，获取不同模型，对测试集上的预测误差值进行了对比分析。实验表明加入地理位置信息后，预测准确性有一定提高,说明地理位置与房价存在一定联系。又将原始数据集分成房龄小于等于0，小于等于33，大于33并且小于67，大于67等不同房龄数据集。实验表明使用不同房龄数据集建立ANFIS模型，房龄越小预测准确性越高，房龄较大的房产预测准确性较差，说明房龄与房价有密切关系。

结合日常房产评估经验，提出基于k近邻的ANFIS改进方法。定义不同意义的k近邻,描述了查找k近邻，计算k近邻均价算法，并应用于ANFIS模型，从而将地理位置信息，时间信息与历史房价相结合。实验表明，时空k近邻，空间k近邻方法的预测准确性有大幅提高,k取10时，时空k近邻平均MAPE为9.86%；在MAPE的5%范围内，时空k近邻为42.4%，说明使用k近邻改进自适应神经模糊推理系统的方法，能明显改进房价预测准确性，这一方法也可应用于其他大宗财产评估。k近邻的k值选取20与k值选取10时，有相似的结论，但k为20时，全变量k近邻、空间k近邻、时空k近邻的RMSE,MAE值，普遍稍有增加，说明k近邻的k值选取过大,可能会引起误差增大。

由于不同房产属性与价格的非线性关系，房产评估是一个较复杂的过程，自适应神经模糊推理系统对房产评估是非常有效手段，特别是通过应用k近邻方法进行改进，对输入数据集进行优化，能明显改进ANFIS的预测效果。该方法的提出，有效地提高了ANFIS自适应神经模糊推理系统的预测准确性。

随着计算机信息系统的广泛应用，存储技术的发展，电子商务的兴起，可以获得大量的历史数据，使用历史数据评估大宗财产的价值，越来越多地引起重视，我们将应用人工智能方法进一步改进神经模糊推理系统，并将它应用于其它大宗财产评估领域。

[1]Jian Guan, Jozef Zurada, Alan S.Levitan.An Adaptive Neuro-Fuzzy Inference System Based Approach to Real Estate Property Assessment.[J].The Journal of Real Estate Research, 2008,30(4):349-387.

[2]Jozef Zurada, Alan S.Levitan, Jian Guan.A Comparison of Appraisal Context.[J].The Journal of Real Estate Research, 2011,33(3):395-421.

[3]Mitchell, T.Machine Learning [M].New York :McGraw-Hill, 1997.

[4]Worzala, E, Lenk, M., and Silva, A.An exploration of neural networks and its application to real estate valuation.[J].The Journal of Real Estate Research, 1995,10(2):185-201.

[5]Nguyen, N., and A.Cripps.Predicting housing value:a comparison of multiple regression analysis and artificial neural networks.[J].The Journal of Real Estate Research,2011, 22(3):313-336.

[6]Ponnambalam, K., Karray, F., Mousavi, S.Optimization Approaches for Reservoir Systems Operation Suing Computational Intelligence tools.[J].SAMS, 2002,42(9):1347-1360.

[7]Stepnowski, A., Mosynski, M., Dung, T.V.Adaptive Neuro-Fuzzy and Fuzzy Decision Tree Classifiers As Applied Seafloor Characterization.[J].Acoustical Physics,2003,49(2):193-202.

[8]Hasiloglu, A., M.Yilmaz, O.Comakli, and I.Ekmekci.Adaptive Neuro-Fuzzy Modeling of Transient Heat Transfer in Circular Duct Air Flow.International Journal of Thermal Science, 2004, 43:1075-90.

[9]Byme, P.Fuzzy Analysis:A Vague Way of Dealing with Uncertainty in Real Estate Analysis.Journal of Property Valuation & Investment, 1995, 13(3):22-41.

[10]Bagnoli, C., B.Smith, and C.Halbert.The Theory of Fuzzy Logic and its Application to Real Estate Valuation.Journal of Real Estate Research, 1998, 16(2), 169-200.

[11]Sugeno, M.and Kang, G.T., Structure identification of fuzzy model.[J].Fuzzy Sets and Systems, 1988,28(1):15–33.

[12]Takagi, T.and Sugeno, M., Fuzzy identification of systems and its applications to modeling and control.[J].IEEE Transactions on Systems, Man, and Cybernetics 1985,15(1):116–132.

[13]Ian H.Witten & Eibe Frank.Data Mining Practical Machine Learning Tools And Techniques [M].San Francisco:Elsevier, 2005.