基于核正交半监督鉴别分析的人脸识别算法

王燕, 刘花丽, 苏文君

WANG Yan , LIU Huali, SU Wenjun

兰州理工大学 计算机与通信学院，甘肃 兰州 730050

College of Computer and Communication, Lanzhou University of Technology, Lanzhou 730050, China

1 引言

人脸识别因其在身份验证和识别场合具有巨大的应用价值，以及对模式识别理论的发展具有重要的学术意义而备受关注。在人脸识别中，如何有效地从高维数据中提取具有高可分性的低维特征是特征提取的关键。而众多度量可分性准则的算法中，主成分分析（PCA）[1]和线性判别分析（LDA）[2]是最具有代表性的算法。

近几年涌现出许多流形学习方法来发现人脸图像数据中的非线性流形结构，如等距映射（ISOmetric MAPping，ISOMAP）[3]、局部线性嵌入（Locally Linear Embedding，LLE）[4]、拉普拉斯特征映射(Laplacian Eigenmap，LE)[5]。但是，以上三种方法应用于人脸识别时不能有效的处理新来的样本点[6]。为了克服这一问题，学者们将线性映射的思想引入人脸识别，较为典型的算法包括局部保持投影(Locality Preserving Projection，LPP)[7]、边界 Fisher分析(Marginal Fisher Analysis，MFA)[8]和无监督判别投影(Unsupervised Discriminant Projection，UDP)[9]。这些算法旨在保留原始人脸图像数据中的局部邻域信息，从而试图发现隐藏在人脸图像数据中内在的低维非线性局部结构。然而当有类别标签的人脸样本数据不足时，有监督算法的泛化能力降低。需要说明的是，获取样本的类别信息十分耗时，而无标签的数据相对来说容易得到，半监督分类利用大量廉价的无标签样本信息来增加分类的精确度[10]。而这些算法都是线性的，不能更好地发掘样本中的高阶非线性因素。随着核函数在支持向量机(Support Vector Machine,SVM) 中的成功应用, 出现了如核邻域保持投影(KernelNPP,KNPP)[11]及核无监督判别分析(KernelUDP,KUDP)[12]等非线性子空间方法，更好地发掘人脸受光照、姿态和表情等影响的非线性因素。但对于分类问题不能提取出最具有鉴别性的特征。文献[13]提出核空间正交及不相关邻域保持鉴别嵌入算法，能够利用样本的类别信息，但是不能充分利用无标记样本信息。

为此，本文针对非线性和有标记样本不足问题，提出了一种基于核正交半监督鉴别分析的人脸识别算法。在核空间，其目标函数是在监督算法MFA的基础上，将UDP的局部和非局部散度矩阵引入，改进为半监督的算法，同时保证各向量正交。该算法不仅能有效地提取人脸图像的非线性结构信息，而且将监督算法浪费的无标签样本和无监督算法没有利用分类的标签信息充分利用，进一步提高了分类的鲁棒性。

2 半监督鉴别分析

2.1 边界Fisher判别分析

MFA的目标是将k1近邻的样本拉近的同时将k2近邻的样本推远。其好处是避免少数几个相距较远的样本主导，避免了 LDA满足高斯分布这一条件。假设{(x1, l1),(x2, l2),…,(xN,lN)}为人脸训练样本数据集，其中，xi∈RD表示一个D维向量，li∈L={1,2,…,c}是样本xi的类别标签，L为类别标签集。数据点xi通过投影矩阵WD×d可以得到低维映射yi∈Rd,d＜D ，即

MFA定义类内散布矩阵Sw来表示同类数据点的集中程度：

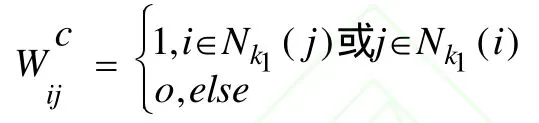
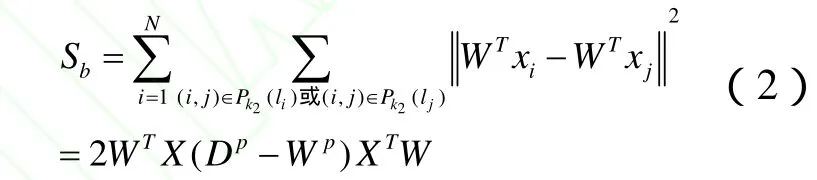
2.2 无监督判别分析

UDP是Yang等[9]人提出的一种流形学习的线性化算法。除了反映人脸样本间的内在数据关系外，还能够对人脸样本进行有效分类。UDP的目标就是最大化非局部散度与局部散度的比，得到有效的分类方向，从而使样本数据点在该方向上投影。为此，我们定义一个N×N的邻接矩阵H如下所示：

局部散度 JL(W)能够将高维空间中靠的近的样本点降到低维空间中仍然保持近邻关系，其定义如下：

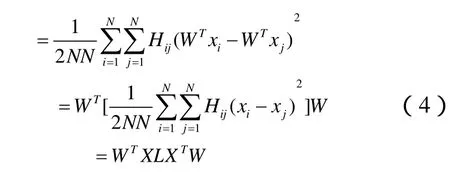
非局部散度 JN(W)不同于局部散度，是将高维空间中非近邻的样本点降维后保持疏远关系。其定义如下：

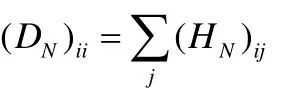
局部散度矩阵SL、非局部散度矩阵SN分别定义为：

基于UDP准则思想，最小化局部散度的同时最大化非局部散度。其目标函数定义如下：

2.3 半监督鉴别分析

将高维空间中同类近邻的人脸样本点在低维空间中仍然保持近邻关系，而异类近邻点在低维空间中保持疏远关系。同时，考虑到有标记的人脸样本不足问题，将MFA和UDP进行结合，其目标函数形如UDA[14](UDP—based Discriminant Analysis)表示如下：

其中：Sb和Sw通过有标签人脸训练样本计算而来，即 MFA算法中的类间散布矩阵和类内散布矩阵。JN和JL是通过全部数据集计算出来的，即UDP算法中的非局部散布矩阵和局部散布矩阵。α和β用来调节JN和JL的贡献度的常系数。

3 核正交半监督鉴别分析

假设存在一个非线性映射φ:RD→H,H表示高维内积空间。φ(xi)是xi在H中的值，对于空间H中φ(xi)与φ(xj)间的距离，定义为,其中,是核矩阵K的(i, j)个元素。表示H中的内积运算，称为核函数。常用的核函数主要包括：1）线性核函数：多项式核函数：K(x, y)=(1+xTy)d；3）高斯核函数：

3.1 算法推导

本文算法的目的是对H中数据点φ(X)=[φ(x1),φ(x2),…,φ(xN+M)]通过线性映射 Z=WTφ(x)进行降维，并将人脸图像映射为l维空间中的新样本数据点： Z=[z1, z2,…,zN+M]。核空间转换矩阵中的W={w1,w2,…,wn}的列向量wt(1 ≤t≤n)是 由φ(X)=[φ(x1),φ(x2),…,φ(xN+M)]张成，故存在一组系数B={b1, b2,… bN+M}，使得

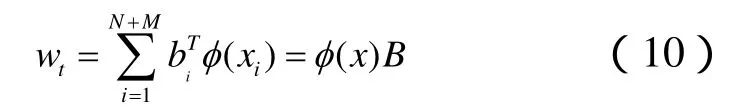
则可定义核空间类内散布矩阵如下：

其中 KN=φ(XN)Tφ(X)。

核空间类间散布矩阵为：

核空间局部散度矩阵如下所示：

其中 K=φ(X)Tφ(X)。

核空间非局部散度矩阵表示如下：

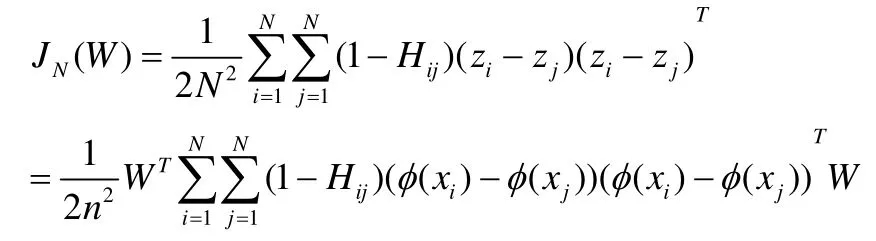
本文算法旨在寻求一组满足正交条件且最大化核空间目标函数的基向量。核正交半监督鉴别分析的目标函数表示如下：

利用拉格朗日乘数，以上受约束最小化问题可以转换成如下方程：

最终通过对以上方程求解可得：

bk为方程(18)的最小特征值对应的特征向量。其中，最后得到核空间的投影矩阵 B=[b1, b2,…,bl]，对于输入样本xi，其在核空间的半监督鉴别分析即为；其中 表示 的第 个元zmi素。

3.2 算法步骤

核正交半监督判别分析步骤如下:

Setp 1.选择合适的核函数，将人脸的训练集样本数据映射至高维特征空间。

Step2.构造近邻图。对任意 xi∈XN，选择人脸图像的同类点邻域，异类点邻域以及全局邻域。

Setp3.根据式（11）、（12）、（13）和（14），分别计算人脸训练集数据在H 中的Sw、Sb、JL和JN。

Step4.求解式（16）和（18），得到l个最大特征值对应的一组特征向量 B=[b1, b2,…,bl]。

Step5.对人脸的训练样本和测试样本进行非线性降维，采用最近邻分类器对特征分类，确定人脸测试样本集所属的类别。

4 人脸识别实验

在ORL和YALE人脸库上分别进行实验来验证本文算法的性能，并与PCA，LDA，LPP，MFA、UDP进行对比。实验中，参数α和β均设置为0.1，采用了高斯核函数k(x, y)=exp()，式中高斯核参数中的δ为经验值，取δ=5.5e+7。LPP、MFA、UDP以及本文算法中k近邻参数k取 3。实验用最近邻分类器来分类，识别率取 10次实验的最大平均值。所有人脸图像为灰度图像，本文使用的人脸图像经裁剪后大小均为32×32像素。

4.1 ORL人脸数据库的实验

ORL人脸库是由英国剑桥大学建立，包括 40个人，每个人10张112×92的在不同时间采集的正面人脸图像组成。其中包括不同视角、不同表情（高兴、微笑、生气、吃惊、闭眼、睁眼等）和不同面部细节（戴或不戴眼镜、有或无胡须、不同发型），人脸姿态有变化和旋转不超过 20°。图 1所示的是来自ORL人脸库的某一人的10张图像。

图1 ORL人脸库图像示例

对于 ORL人脸库的实验验证，随机地从每个人的图片中选择 L(L=3,4,…,7)张图片作为训练样本，余下的10-L张图片作为测试样本。其中，监督算法LDA和MFA在训练时所采用的全是具有标签信息的训练样本。而在本文算法训练时只需要使用到2个带有标签的人脸样本，余下的训练样本就是把标签信息去掉的样本。如下表1为六种算法分别在不同训练样本的情况下识别率的对比，而图2是这六种算法均采用4个训练样本降到不同维数的识别率的对比。

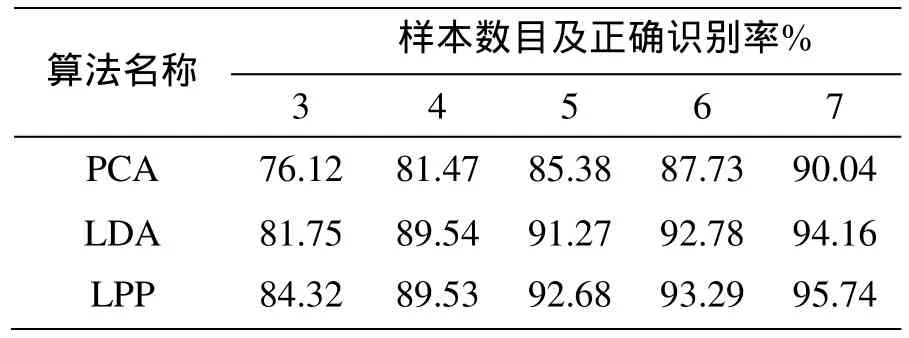
表1 ORL人脸库上的识别结果比较

MFA 85.68 90.80 93.38 95.63 96.72 UDP 84.92 90.23 93.24 94.58 96.53本文算法 91.59 95.47 97.86 98.16 98.78

图2 ORL人脸库的4Train的识别率

从表1和图2可以看出，本文算法在ORL人脸库上能够取得最高的识别率。在有标记训练样本为2张人脸，并利用其余无标记样本时，本文算法在维数为38时达到最高识别率95.47%，且在特征维数达到38以后, 基本稳定在一个特定范围。同时可看出，MFA和UDP算法的识别率高于LDA和PCA算法的识别率。

4.2 YALE人脸数据库的实验

YALE人脸库由15个人，每个人有11张共165张图像组成。这些图像在光照条件下变化比较大，而且面部表情（正常、惊讶、伤心、开心和眨眼等）和细节（戴或不戴眼镜、有或无胡须）也有比较明显的变化。YALE人脸库中的某一个人的11张图像如图3所示。

图3 YALE人脸库图像示例

在YALE人脸库实验中，也是随机地从每个人的图像中选取 L(L=3,4,…,7)张图片作为训练样本，而余下11-L张作测试样本。在YALE中对于带有标签信息和不带标签信息的人脸样本选取和 ORL相同。如下表2为六种算法在不同训练样本情况下识别率的对比，而图4是六种算法均采用4个训练样本降到不同维数的识别率的对比。

表2 YALE人脸库上的识别结果比较

PCA 49.32 53.74 56.03 58.60 60.53 LDA 58.47 69.80 73.62 78.31 79.65 LPP 68.35 76.76 77.24 80.33 83.85 MFA 68.15 77.37 81.12 83.68 86.03 UDP 68.23 77.14 79.58 82.39 85.80本文算法 71.53 81.52 83.17 85.45 89.86

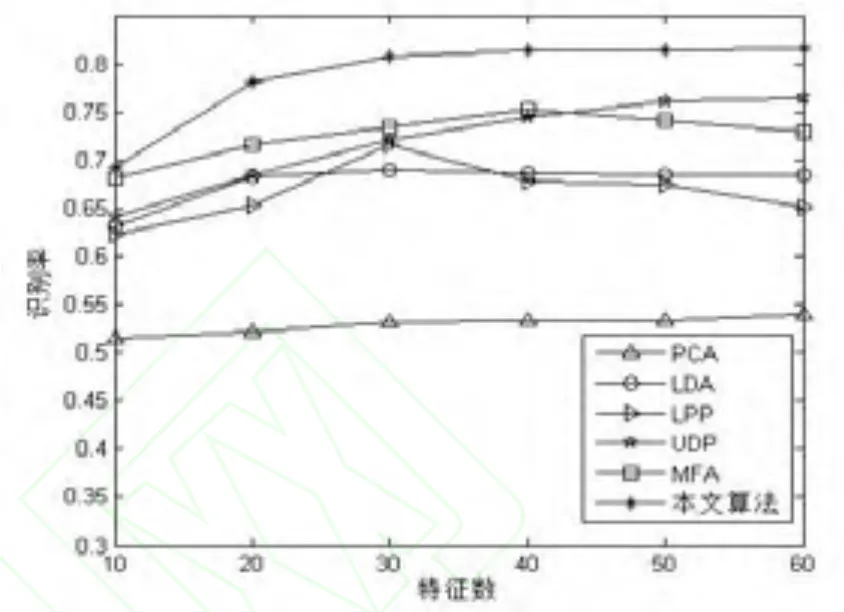
图4 YALE人脸库的4Train的识别率

从表2和图4可以看出，由于YALE库的图像受姿态、光照、表情变化的干扰较大，因此文中所列的所有方法的识别率相对较低。从实验结果可以看出，PCA和LDA保持全局线性结构进行维数约减，不能很精确地描述非线性流形，其识别率最低。本文算法在维数为54时达到最高识别率81.52%，高于LPP，MFA及UDP的识别率。LPP，MFA和UDP算法最高识别率分别为 76.76%，77.37%和77.14%，它们的特征维数分别为28，39和56时取得最大识别率。

4.3 实验分析

本文算法在MFA的基础上，将无监督UDP加入到目标函数中，并引入核技巧在保证特征空间各向量相互正交的条件下，可得到利于有效分类的投影矩阵。实验表明，本文算法对于姿态、表情、光照等变化体现出极强的鲁棒性，相比其它几种算法，识别效果是最优的。该算法在核空间中利用了样本空间的判别信息和局部几何结构，当仅有少量的标签样本时，可以利用大量的无标签样本帮助估计数据的流形结构，提高学习性能。作为识别来说，更多的特征将会引入不利于分类的信息，当维数达到一定的程度，识别率不再会因维数的增加而提高，甚至可能有所下降。而MFA仅仅利用有限的有标签样本，LPP、UDP利用无标签样本，同时这些算法实质上是线性的，所以识别率低于本文算法。PCA的识别率低于LDA，这是由于PCA是无监督的。LDA的识别率要比MFA低，MFA的识别率也比本文算法低，这说明核正交半监督鉴别分析能够取得比较理想的性能。

5 结束语

本文针对流形学习算法中非线性和有标签样本不足问题，提出了一种核正交半监督鉴别分析的人脸识别方法，使用高斯核函数，在核空间中提取人脸非线性特征，并保证各向量间相互正交，从而更有效的提取出人脸非线性局部结构。算法既能充分利用有标记样本的监督信息，又能挖掘出隐藏在无标记数据中的潜在信息，很好的保持了数据的局部和全局信息。然而，由于核函数的选择都是根据经验来选取的，至今还没有一个确定的理论依据和选择标准。因此，如何更有效地利用核空间发掘人脸图像中非线性高维数据的本质的、内在的结构将是今后的一个研究方向。

[1]Turk M,Pentl and A.Eigenface for recognition [J].Journal of Cognitive Neuroscience, 1991, 3(1):72-86.

[2]Belhumeur P,Hespanha J,Kriegmand D.Eigenfaces vs.Fisherfaces:Recognition using class specific linear projection[J].Pattern Analysis and Machine Intelligence,1997, 19(7) :711-720.

[3]Tenenbaum J B,Desilva V,Langford J C.A global geometric framework for nonlinear dimensionality reduction[J].Science, 2000, 290(5500):2319-2323.

[4]Roweiss L,Saul L.Nonlinear dimensionality reduction by locally linear embedding[J].Science, 2000,290(5500):2323-2326.

[5]Belkin M,Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation, 2003, 15(6):1373-1396.

[6]Bengio Y,Palement J,Vincent P,et al.Out-of-sample extensions for LLE, isomap, MDS, eigenmaps, and spectral clustering[J].Neural Computation, 2004, 16(10):2179-2219.

[7]He Xiaofei, Yan Shuicheng, Hu Yuxiao, et al.Face Recognition Using Laplacianfaces[J].IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(3):328-340.

[8]Yan Shuicheng, Xu Dong, Zhang Benyu, et al.Graph Embedding and Extensions:A General Framework for Dimensionality Reduction[J].IEEE Trans on Pattern Analysis and Machine Intelligence, 2007, 29(1):40-51.

[9]Yang Jian,Zhang D,Yang Jingyu,et al.Globally Maximizing, Locally Minimizing:Unsupervised Discriminant Projection with Applications to Face and Palm Biometrics[J].IEEE Trans on Pattern Analysis and Machine Intelligence, 2007, 29(4):650-664.

[10]魏莱,王守觉.基于流形距离的半监督判别分析[J].软件学报,2010, 21(10):2445-2453.

[11]庞彦伟,俞能海,沈道义,刘政凯.基于核邻域保持投影的人脸识别[J].电子学报,2006,34(8):1542-1544.

[12]王庆军,张汝波,潘海为.核正交UDP及其在人脸识别中的应用[J].计算机辅助设计与图形学学报，2010,22(10):1783-1787.

[13]刘冠群,王庆军,张汝波,潘海为.核空间正交及不相关邻域保持鉴别嵌入算法[J].哈尔滨工程大学学报，2011,32(7):938-942.

[14]Qiu H N, Lai J H, Huang J, et al.Semi-supervied discriminant analysis based on UDP regularization[C].Proc of the 19th International Conference on Pattern Recognition.Tampa:IEEE, 2008:1-4.