多传感器集中式增量卡尔曼滤波融合算法

2014-04-03马丽丽陈金广

计算机工程与应用 2014年11期

关键词：系统误差卡尔曼滤波增量

马丽丽，张曼，陈金广

MA Lili,ZHANG Man,CHEN Jinguang

西安工程大学计算机科学学院，西安 710048

School of Computer Science,Xi’an Polytechnic University,Xi’an 710048,China

1 引言

状态估计被广泛应用于航空、航天、航海、工业过程控制、目标跟踪等各个领域。不同的估计准则会产生不同的估计算法。其中最具代表性的是卡尔曼滤波算法，该算法采用递推形式，数据存储量小，适用范围广，具备其他滤波形式所不具备的优点。该滤波理论一经提出便得到了广泛应用。然而，在实际应用过程中，由于周围环境的影响、测量设备自身造成的误差、模型和参数选取不当等原因，会产生量测系统误差，而使用传统卡尔曼滤波算法难以消除该类系统误差。

近年来，傅惠民等人针对该问题，提出了一系列增量滤波算法。在文献[1]中，针对传统卡尔曼滤波算法无法消除量测系统误差的情况，提出了增量卡尔曼滤波算法，成功地消除了量测系统误差，提高了滤波精度。随后，为了将该思路扩展到非线性系统，文献[2]提出了扩展增量卡尔曼滤波算法，文献[3]提出了增量粒子滤波算法。然而，以上算法仅适用于单传感器滤波系统，而实际中的许多估计问题（例如军事指挥和工业控制等方面）都涉及多个传感器。多传感器数据融合算法通常分为集中式、分布式和混合式三类，已经有许多可供借鉴的成熟算法[4]。人们对于多传感器融合算法进行了很多研究[5-8]，其中在序贯滤波[9-14]和扩维滤波[15-16]方面的应用研究也取得了成果。

考虑到传统增量卡尔曼滤波算法不能解决多传感器情况的估计问题，本文将傅惠民等人提出的增量卡尔曼滤波算法分别与传统扩维融合算法和传统序贯融合算法相结合，提出增量卡尔曼滤波的扩维融合算法和增量卡尔曼滤波的序贯融合算法。该算法将单传感器增量卡尔曼滤波算法扩展到多传感器中，可以充分利用多个数据源的信息，能够增强滤波的可靠性和系统的生存能力，克服了传统增量卡尔曼滤波算法仅适用于单传感器的情况，同时采用增量的滤波算法还能消除传统扩维融合算法和传统序贯融合算法中量测系统误差造成的影响，提高滤波精度。

2 问题描述

在多个传感器的目标跟踪系统中，目标运动的状态方程一般表示为：

其中，xk∈ℝn表示目标在k时刻的状态向量，Φk∈ℝn×n表示系统状态转移矩阵，Γk∈ℝn×r表示系统噪声分布矩阵，wk∈ℝr表示系统噪声向量。假设wk服从高斯分布，其均值为0，方差为Qk。目标初始状态为 x0，且cov[wk，wj]=Qkδkj，cov[x0，wk]=0 。

假设有N个传感器对同一目标进行量测，则相应的量测方程可以表示为：

在式（2）的基础上，构造多传感器增量量测方程为：

3 扩维增量卡尔曼滤波

在扩维融合（也称并行滤波）算法中[4]，通常令：

那么在融合中心，对所有传感器量测的量测方程可以统一表示为：

对所有传感器的增量量测方程可以写为：

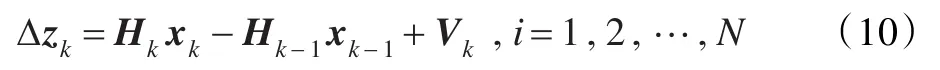
根据式（2）的假设条件，可得：

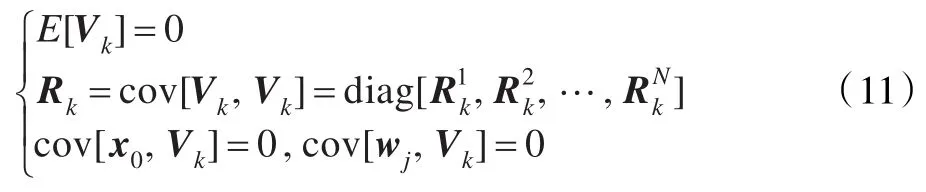
则式（1）和式（10）分别为扩维增量卡尔曼滤波的状态方程和增量量测方程。假设k-1时刻的状态估计值为相应的协方差为Pk-1|k-1，则k时刻的状态预测方程为：

相应的协方差矩阵为：

根据卡尔曼滤波方程，状态估计方程为：

相应的协方差矩阵为：

其中：

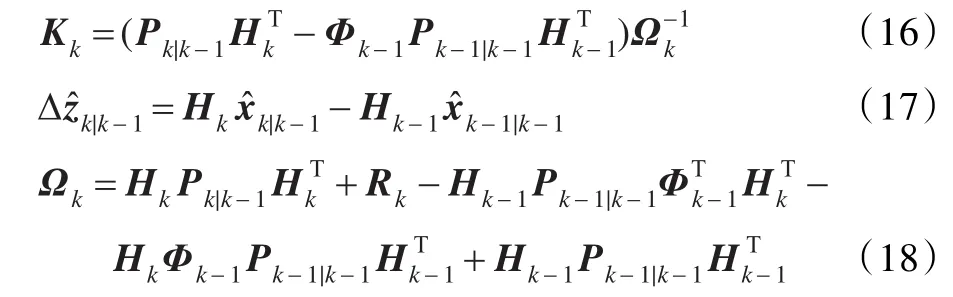
注意到在式（16）中包含矩阵求逆运算，由于该类运算的时间复杂度随着矩阵维数的增长而呈指数增长，因此，当融合的传感器数目过多时，时间复杂度会急剧增大。此外，多个传感器融合之后的误差性能与数据的冗余性和互补性密切相关。如文献[5]所述，若多传感器的量测数据之间为负相关时，则融合后的误差性能较好；若多传感器量测数据之间为正相关时，则融合后的误差性能退化。

4 序贯增量卡尔曼滤波

序贯滤波是指当各个传感器在同一时刻的量测噪声不相关时，可以依据量测噪声方差的大小，由小到大对传感器进行编号，在融合中心按照传感器的序号分别获取各传感器的量测值，依次对当前状态进行更新。

对于式（1）和式（3）所描述的多传感器增量滤波方程，融合中心按照传感器1→N的顺序对目标的运动状态估计值进行序贯更新。更新过程为：假设第i(1≤i≤N)个传感器在k-1时刻的状态估计值为相应的协方差为那么根据系统状态转移方程，由式（12）和式（13）可以获得k时刻的状态预测值及其协方差矩阵当处理中心接收到传感器1的量测值后，由式（3）可以计算传感器1的增量量测值，利用对状态预测值及其协方差进行更新，更新公式为：

假设利用第i个传感器量测值进行更新之后的状态估计值及其协方差分别为，则当处理中心接收到第i(1＜i≤N)个传感器的量测值后，状态更新方程为：

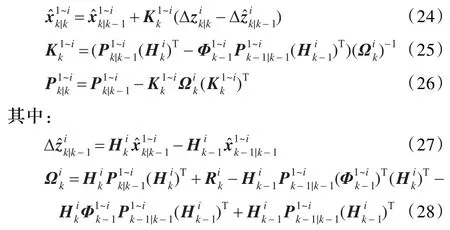
按照上述更新规则，依次对k时刻的N个量测值进行更新，则最终融合中心对系统状态的序贯滤波估计为，相应的协方差为。

5 实验模型及结果分析

本文用线性和非线性两个例子来验证多传感器增量卡尔曼滤波融合算法的有效性。

实验1假设一维线性离散系统为[1]：

其中，i表示传感器序号，实验中采用3个传感器。Wk和分别是k时刻的系统噪声和量测噪声，且均为独立的高斯白噪声。Wk的均值q=0，方差Q=0.1，的均值为0，方差R1=R2=R3=1，它们均为已知量。是量测系统误差，为未知量，方便起见，假设。需要指出的是，该例中的。

分别采用传统扩维卡尔曼滤波、扩维增量卡尔曼滤波、传统序贯卡尔曼滤波和序贯增量卡尔曼滤波四种算法进行融合。设初始状态 X0=10 ，相应的协方差为P0=0.1。图1是利用四种融合算法获得的状态估计结果。由图可见，传统扩维卡尔曼滤波和传统序贯卡尔曼滤波的结果相对于真实状态都有较大的偏移，未能消除量测系统误差。而扩维增量卡尔曼滤波和序贯增量卡尔曼滤波的结果基本与真实状态吻合得很好。图1表明，扩维增量卡尔曼滤波和序贯增量卡尔曼滤波能够有效消除量测系统误差，提高融合精度。图2是四种融合算法得到的状态估计结果的误差。由图可见，扩维增量卡尔曼滤波和序贯增量卡尔曼滤波的波动很小，误差表现较为平稳，基本在0附近。然而，传统扩维卡尔曼滤波和传统序贯卡尔曼滤波与真值的误差值一直很大。相比较而言，在多传感器情况下，扩维增量卡尔曼滤波和序贯增量卡尔曼滤波能够获得更高的状态估计精度，能够消除未知系统误差对其造成的影响。

图1 实验1中不同融合算法的状态估计

图2 实验1中不同融合算法的状态估计误差

为了说明几种融合方法的运算复杂度，表1列出了四种方法各运行100次的平均运行时间。由表1可知，时间复杂度由高到低依次为：序贯增量融合、标准序贯融合、扩维增量融合和标准扩维融合。考虑到滤波算法中有求逆运算，因此随着系统模型维数的增加，扩维融合和序贯融合算法之间的时间复杂度关系会发生变化。

为了研究算法误差对过程噪声的敏感性，设定噪声方差分别为0.1，0.2，0.5，1.0，1.1，1.2，采用 Monte Carlo方法重复执行100次，计算相应的均方根误差如表2所示。由表2可知，随着过程噪声方差的增大，四种方法求得的误差也随之增大。

表1 不同方法的运行时间

表2 不同过程噪声方差下的均方根误差

实验2假设一维非线性离散系统为[2]：

其中，i表示传感器序号，实验中采用3个传感器。Wk和分别是k时刻的系统噪声和量测噪声，且均为独立的高斯白噪声。Wk的均值q=0，方差Q=0.1，的均值为0，方差R1=R2=R3=1，它们均为已知量。是量测系统误差，为未知量，方便起见，假设。

由于该模型的系统状态方程是线性方程，因此只需将系统的非线性增量量测方程采用一阶泰勒级数展开的办法进行线性化，则其中的Hk和Hk-1分别为：

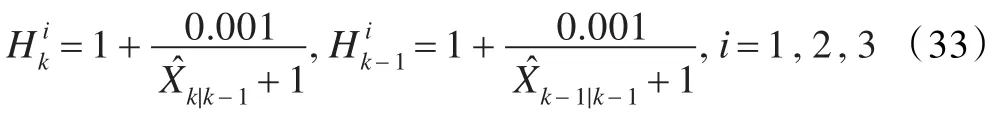
分别采用传统扩维EKF、扩维增量EKF、传统序贯EKF和序贯增量EKF四种算法进行融合。设初始状态X0=10 ，相应的协方差为P0=0.1。图3是利用四种融合算法获得的状态估计结果。由图可见，传统扩维EKF和传统序贯EKF的结果相对于真实状态都有一定量的偏移，未能消除系统误差，而扩维增量EKF和序贯增量EKF的滤波结果能够与状态真值较好的吻合，偏差很小，消除了系统误差。图4是四种融合算法得到的状态估计结果的误差。由图可见，扩维增量EKF和序贯增量EKF的滤波结果误差较小，基本在0附近波动。然而，传统扩维卡尔曼滤波和传统序贯卡尔曼滤波与真值的误差值一直很大。相比较而言，在多传感器情况下，扩维增量卡尔曼滤波和序贯增量卡尔曼滤波能够获得更高的状态估计精度，能够消除未知系统误差对其造成的影响。

为了考察几种融合算法的时间复杂度，表3列出了四种方法各运行100次的平均运行时间，由表3可知，时间复杂度由高到低依次为：序贯增量融合、标准序贯融合、扩维增量融合和标准扩维融合。这与实验1的结果相似。

图3 实验2中不同融合算法的状态估计

图4 实验2中不同融合算法的状态估计误差

表3 不同方法的运行时间

为了研究过程噪声方差对算法误差的敏感性，设定噪声方差分别为 0.1，0.2，0.5，1.0，1.1，1.2，采用 Monte Carlo方法重复执行100次，计算相应的均方根误差如表4所示。由表4可知，随着过程噪声方差的增大，四种方法求得的误差也随之增大。这与实验1的结果相似。

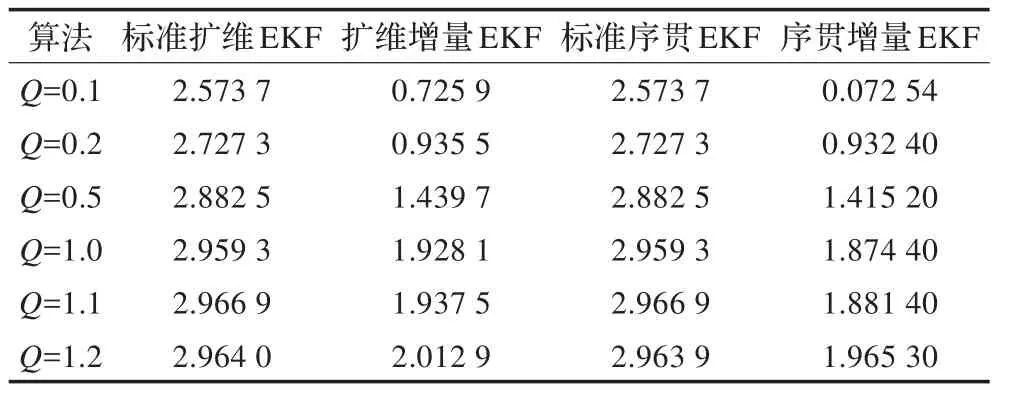
表4 不同过程噪声方差下的均方根误差

6 结论

本文将增量卡尔曼滤波分别与集中式融合算法中的并行滤波和序贯滤波相结合，提出多传感器增量卡尔曼滤波融合算法，即：扩维增量卡尔曼滤波和序贯增量卡尔曼滤波。该算法将单传感器的增量卡尔曼滤波扩展到具有多传感器的增量卡尔曼滤波，与单传感器比较，多传感器能够充分利用多个传感器的资源，有利于时间和空间上信息的互补。例如当某个传感器不能利用或某个目标不在该传感器的覆盖范围内时，则可由其他传感器提供信息，增强了系统的健壮性和可靠性。由于采用增量融合的方法，因此本文算法保留了单传感器增量卡尔曼滤波的优点，即能够成功消除系统误差，提高滤波精度。本文仅给出了一维情况下的例子，对于状态向量为多维的情况，还需要在今后的工作中结合实际应用做进一步的实验验证。

[1]傅惠民，吴云章，娄泰山.欠观测条件下的增量Kalman滤波方法[J].机械强度，2012，34（1）：43-47.

[2]傅惠民，娄泰山，吴云章.欠观测条件下的扩展增量Kalman滤波方法[J].航空动力学报，2012，27（4）：777-781.

[3]傅惠民，娄泰山，吴云章.增量粒子滤波方法[J].航空动力学报，2013，28（6）：1201-1207.

[4]韩崇昭，朱洪艳，段战胜.多源信息融合[M].2版.北京：清华大学出版社，2010.

[5]陈金广，马丽丽，陈亮.多传感器量测噪声对航迹融合性能影响分析[J].火力与指挥控制，2010，35（7）：123-125.

[6]朱安福，景占荣.多传感器信息融合的目标跟踪研究[J].计算机工程与应用，2009，45（25）：7-9.

[7]葛泉波，李文斌，孙若愚，等.基于EKF的集中式融合估计研究[J].自动化学报，2013，39（6）：816-825.

[8]王永安，何光进，刘毅.基于卡尔曼滤波的多传感器跟踪融合算法[J].船电技术，2013，33（2）：4-7.

[9]孟凡彬，郝燕玲，张崇猛，等.基于无迹粒子PHD滤波的序贯融合算法[J].系统工程与电子技术，2011，33（1）：30-34.

[10]章飞，孙睿.多传感器序贯势分布概率假设密度滤波[J].江苏科技大学学报：自然科学版，2012，26（6）：587-592.

[11]郭路，康鹏.序贯滤波在双站无源定位中的应用研究[J].现代防御技术，2008，36（4）：116-119.

[12]王鹏，宋鹏云，张继业.标量及对角阵加权的序贯估计融合算法[J].计算机工程与应用，2012，48（32）：101-104.