基于代数连通性的复杂网络割边模型研究

赵富强,张 烁,何 丽,邢恩军

1 引言

随着近 10年来许多社会网络媒体的迅猛发展，例如Twitter、Facebook和Google+等社交网站，社会网络拥有更庞大的数据量，节点个数达到百万甚至上亿的庞大数据[1]。庞大数据的处理也促使了复杂网络模型和方法的发展。复杂网络混合度上升，复杂网络社区的个数不易确定，社区不平衡性问题也显现出来。虽然一些社团发现算法通过一定的割边模型可有效识别复杂网络中的社区，但算法的复杂度依然很高，割边效率不高，例如，经典社区发现算法Girvan-Newman，该算法的主要缺点是每次迭代只能删除一条边，算法复杂度较高，GN算法的总时间复杂度为O(m2n)；对于稀疏网络，GN算法的复杂度为O(n3) ，其中n为节点数，m为边数。Radicchi等人从提高算法运行效率和如何选择 GN算法层次划分结果中的最优划分出发[2]，提出了一种自包含的GN算法变种[3]。Wilkinson、Huberman和 Tyler在通过采样部分结点来计算边的最短路径介数的方法，提高了算法的计算速度，但计算精度有所降低。Chen和Yuan指出，因为在计算边介数时考虑了所有可能的结点间最短路径，GN算法给出的社团划分往往是不均衡的，据此提出了一种只考虑结点间结点不相交的所有最短路径来计算边的介数的GN算法变种[4]。Fortunato等人则提出利用信息中心度（information centrality）的方法来判断社团之间的边，信息中心度高的结点往往对应于社团之间的边[5]。虽然该 GN算法变种在网络社团结构比较模糊的情况下有较好的划分准确性，但其时间复杂度非常高，为O(m3n)，即稀疏网络上为O(n4)。一些学者提出的社团分割模型，但时间复杂度都相对较高，Clauset et al.[6]时间复杂度为O(n log2n)，Duch & Arenas[7]时间复杂度为O(n2logn)，Eckmann & Moses[8]时间复杂度为O(m＜k2＞)，Capocci et al.[9]时间复杂度为O(n2)；Zhou & Lipowsky[10]时间复杂度为O(n3)。如何在保证分割结果准确的基础上，改进割边模型效率，有效降低复杂网络社区发现算法的时间复杂度，快速有效地将网络中的社区挖掘出来，基于代数连通性提出了贪婪谱优化割边模型（Greedy Algorithm Spectral Optimal Cut Edge Model, GACEM）和基于边中心性测度的割边模型（Edge Centrality Cut Model，ECCM）。

2 贪婪谱优化割边模型

图的拉普拉斯矩阵的第二小特征值2λ被定义为代数连通性，如果图是连通的则代数连通性大于零，该值为零时，图被二分；为了改善该方法一次只能把图二分，文献[11]提出了选择头两个特征向量，一次划分三个社区。代数连通性反应了网络中节点间连接的紧密程度，可以用于计算网络的健壮性和系统的可靠性。与传统的连通性测量函数不同，代数连通性函数依赖于网络中连通节点的数量。在随机网络中，代数连通性函数值与节点的个数和平均度负相关。

复杂网络代数连通性函数λ2(L(x))是单调凸函数，如果G1=(V，E1)和G2=(V，E2)中E1⊂E2，则λ2(L1)≤λ2(L2)。在一个复杂网络中如果边越少，则代数连通性越差。可以通过利用L的第二特征向量最小化RatioCut[12]近似求得λ2(L(x)),公式如下：

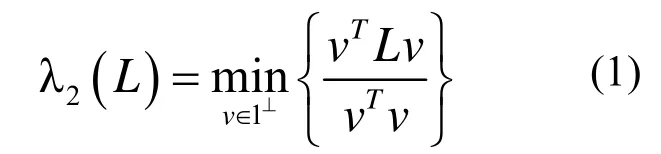
但其时间复杂度较高，可以通过Gossip算法[13]近似计算代数连通性函数，有效降低时间复杂度。由于第二特征值与复杂网络的结构有直接关系，如果网络相对稀疏则第二特征值较小，网络连通性较差，相反则第二特征值较大，网络连通性较好。模型将λ2定义为网络连通性函数2(())L xλ。将通过优化模型选择使网络连通性下降最快的边集。所以最优化问题定义如下：

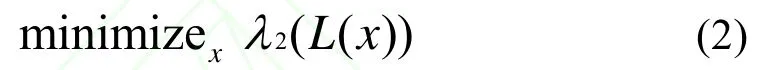
对于复杂网络社区发现问题，主要算法细节如下。给出网络的原始图G=(V,E)和一个常数k，我们将通过模型从E集合中选择k条对代数连通性影响最大的边，假设。公式2被定义为：

这个模型可以被构造为一个布尔函数。图G的每条边可以用一个布尔变量x∈{0,1}m表示。如果边，则相应的xl= 1，否则为0。使L为G对应的拉普拉斯矩阵。公式3被重新定义，变量为x向量：

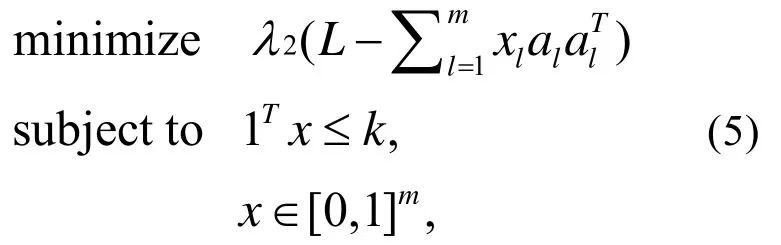
公式(5)给出了公式(4)的上确界，如果公式(5)的最优解是布尔向量，则其结果也是公式(4)的最优解；否则选择x向量中最大的k个值为模型最优解。

边的权重计算可有效用于社区分割中，社区内部的边连接相对密集，社区间的边连接相对稀疏[14]。当复杂网络被分割为两个非连通子图时，是模型本次迭代的结束标志，但复杂网络中节点的度符合幂律分布，大量节点的度小于k，所以删除该节点的边可将该节点剥离出来，形成两个极不对称的非连通子图，从而影响模型社区发现的结果。所以模型根据每条边符权重wl，0≤wl≤1，该权重使连接不同社区间的边权重较大，连接同社区内部节点的边权重较小。在模型优化过程中保持复杂网络的连通特性。权重定义如下所示：

其中l～(i,j)，fi与fj为费德勒向量第i和j分量。

两个社区之间节点的邻接节点往往均匀分布于两个不同社区内部，其对应费德勒向量的值相对较小，所以模型对边l取权重wl与该边连接的两个节点对应费德勒向量的值（fi和fj）成反比，当边l连接两个不同社区内的节点时，则该值权重较小，相反权重较大。考虑权重的优化模型为：

半正定规划（SDP）[15]可以解模型(7)求最优解，但其时间复杂度较高，采用贪婪策略来解决大规模的复杂网络分割问题。

模型首先根据 Newman给出的边介数（edge betweenness）计算每条连接边的中心性，然后根据边中心性值选出前mc个边作为候选删除边，其中k≪mc≪m 。利用模型(7)在mc中选择k条对网络代数连通性影响最大的边。在解模型(7)时，可以采取梯度下降法求得最优解，目标函数的梯度为，代数连通性函数λ2(L(xl))对 xl的偏导数为，其中l～(i, j)。

贪婪策略的启发性步骤如下：

(1) 计算复杂网络中边的介数；

(2) 根据中心性测度选出mc条边作为候选删除边，通过删边学习器模型删除k条边。

由于算法需要计算边的介数，只是在一次删除边的数量上有不同，算法的时间复杂度较高。

3 基于边中心性测度的割边模型

定义1 社会网络的边集中删除一个使该网络代数连通性下降最快的边称为中心边，边所具有的性质称为边中心性（Edge Centrality）。

定义2 社会网络中处于每个社区核心位置的节点称为中心节点。

基于边中心性测度的割边模型（ECCM）与传统的社会网络发现算法不同，模型采取谱分析方法对每条边定义边中心性测度，与传统的利用最短距离，随机游走和节点间的阻抗不同，速度更快，更适合处理大规模社区结构。删除谱中心性最高的节点，然后重新计算剩余节点的谱中心性。快速复杂网络割边模型算法描述如下：

(1) 计算G中每条边的谱中心性测度；

(2) 找到谱中心性最高的边l，删除那条边；更新复杂网络为Gnew。

本模型边的中心性测度是基于代数连通性函数给出的。代数连通性函数的梯度为，其中l～(i, j)，与第二节方法相同。

4 实证分析

(1)真实网络实验

在实验中，采用了真实网络中的football网络，115个节点、613条边。分别采用随机删除一条边、GN方法删除介数值最大的边、GACEM方法删除k条边和ECCM方法；实验结果如图3所示。football网络的初始λ2为1.459001，随机删除120条边，λ2仍然大于1；GN方法，删除60条介数值最大的边后λ2为 0，网络被成功分割，但割边时间较长；GACEM 方法删除 23次后λ2为 0，网络被成功分割，割边时间较GN短，ECCM方法时间更快，后三种方法的分割结果完全一致，即准确率得到验证；实验结果如图1所示。

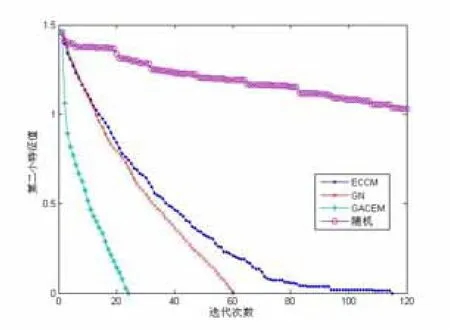
图1 真实网络割边模型比较

图2 模拟网络割边模型比较

(2)模拟网络实验

模拟网络的pout值为0.1，1000个节点，7572条边。网络的初始λ2为0.919444，随机删除80条边，λ2仍然大于0.8；GN方法，删除25条介数值最大的边后λ2为0，网络被成功分割，但割边时间较长；GACEM方法删除8次后λ2为0，网络被成功分割，割边时间较GN短，ECCM方法时间最快，分割结果一致；实验结果如图2所示。

(3)模型复杂度分析

传统的GN分割算法在每次迭代过程中删除一条边中心性最高的边，每次迭代算法的时间复杂度为O(n2m)，其中n为节点数量，m为边数量。与之相较，复杂网络被分割为两个非连通子图前，谱优化社区发现模型每次迭代通过割边学习模型删除k条边，基于Lanczos算法计算拉普拉斯矩阵第二小特征值对应的特征向量（费德勒向量），时间复杂度为O(m1×n)，其中m1为算法迭代的次数，通常要上百次，该算法空间复杂度较高，需要存储m1个n维的 Lanczos向量；然后基于费德勒向量为每条边计算其谱中心性测度，算法时间复杂度为O(m)；从中删除一条谱中心性最高的边时间复杂度为O(m)；使用代数连通性函数λ2(L(Gnew))计算更新后网络的代数连通函数，基于Gossip算法的时间复杂度为O(m2×log(n))，其中m2为算法迭代次数m2为常数。所以割边学习模型执行一次操作的时间复杂度为当复杂网络被分割为两个非连通子图时，算法在每个非连通子图中递归执行，如果并行地在每个子图中执行割边模型，算法执行效率更会显著提升。

5 结论

拉普拉斯矩阵的第二小特征值决定复杂网络的连通性，当该值为零时，网络被二分。传统的割边模型时间复杂度高，为了降低时间复杂度，基于代数连通性提出了贪婪谱优化割边模型和基于边中心性测度的割边模型，通过对真实网络和模拟网络的实验，割边模型使得时间复杂度降低同时，分割结果与GN一致。但模型是否适用于大规模复杂网络、如何把两个模型结合起来进一步降低时间复杂度，值得今后进一步深入研究。

[1]Charu, C., Aggarwal. Social Network Data Analytics[M].Springer Science + Business Media, LLC (2011).

[2]Girvan M, Newman M E J. Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences of the United States of America,2002,99(12):7821-7826.

[3]Radicchi F, Castellano C, Cecconi F, et al. Defining and identifying communities in networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(9):2658-2663.

[4]Chen J, Yuan B. Detecting functional modules in the yeast protein–protein interaction network[J]. Bioinformatics,2006, 22(18):2283-2290.

[5]Fortunato S, Latora V, Marchiori M. Method to find community structures based on information centrality[J].Phys. Rev. E, 2004, 70(5):056104.

[6]Clauset, M.E.J. Newman, C. Moore, Finding community structure in very large networks, Phys. Rev. E 70 (6),2004, 066111.

[7]J. Duch, A. Arenas, Community detection in complex networks using extremal optimization, Phys. Rev. E 72(2), 2005, 027104.

[8]J.-P. Eckmann, E. Moses, Curvature of co-links uncovers hidden thematic layers in the World Wide Web, Proc. Natl.Acad. Sci. USA 99 (2002) 5825-5829.

[9]Capocci, V.D.P. Servedio, G. Caldarelli, F. Colaiori, Detecting communities in large networks[J], Physica A 352,2005, 669-676.

[10]H. Zhou, R. Lipowsky, Network brownian motion: A new method to measure vertex-vertex proximity and to identify communities and subcommunities[J], Lect. Notes Comput. Sci. 3038, 2004, 1062-1069.

[11]Thomas Richardson, Peter J. Mucha, and Mason A. Porter.Spectral tripartitioning of networks[J]. Physical Review E,2009, 80(3):036111:89.

[12]Ren-Cang Li. Accuracy of Computed Eigenvectors via Optimizing a Rayleigh Quotient[J]. BIT Numerical Mathematics 2004,44(3) :585-593.

[13]S. Boyd, A. Ghosh, B. Prabhakar, and D. Shah, Gossip algorithms: Design, analysis and applications[J], Proceedings of IEEE Infocom ,2005, 3:1653-1664.

[14]Z. Xia, Z. Bu, Community detection based on a semantic network[J], Knowledge Based Systems, 2012, 26:30-39.

[15]Y. Kim and M. Mesbahi, On maximizing the second smallest eigenvalue of a state-dependent graph laplacian[J], IEEE Transactions on Automatic Control, 2006,51(1):116-120.