机器人群通信机制的定时同步技术研究
2014-04-03
(西南科技大学信息工程学院,四川 绵阳 621010)
0 引言
机器人作为一种替代人类在危险、恶劣环境下作业必不可少的工具,可以辅助完成人类无法完成的工作,如空间与深海作业、精密操作、管道内作业等。在日本核危机中,除了工人以外,奋战在一线的还有机器人。在这种紧急的状态下,主要是通过无线通信系统实现各机器人的定位、监控和指挥调度[1]。由于数据收、发端不在一起,要使它们能步调一致地协调工作,必须通过同步系统来保证。同步系统工作性能的好坏,很大程度上决定了机器人通信系统的质量,这对正在特殊环境中作业的机器人及时恢复控制台指令信息、完成作业任务是至关重要的[2-3]。较早使用的位同步技术是早迟门算法[4]。该算法是利用有定时误差时最佳采样点的相邻前后两个采样点的幅度差值不为0的特点来提取定时误差。但是采用早迟门算法时,每个符号至少需要有3个采样点,这对于高数据率的发射机来说很不理想。
鉴于以上缺点,Mueller与Muller在1976年提出了Mueller&Mulle算法[5]。该算法只需要1个采样点,通过估计每个输入符号的定时相位误差,输出与估计符号采样时刻相匹配的信号值。但该方法对载波的频偏比较敏感,需要在同步之前完成载波同步,这给定时误差提取的设计带来一定困难。Gardner提出了一种开环结构的定时误差提取算法——Gardner算法[6]。该算法不需要判决反馈,每个符号只需要两个采样点,避免了前两种方法的缺点。针对同步系统中存在的定时抖动问题,本文提出一种减小定时抖动的方法。通过仿真分析可以看出,该方法对定时抖动有很好的抑制作用。
1 同步技术总体方案
机器人作业的通信可以分为内部通信和外部通信。内部通信主要是各模块、各部件之间的数据交流,协调各个模块间的功能行为;而外部之间的通信较为复杂,主要是各个机器人之间或者是机器人与控制者之间等外部设施的资源共享和信息交互。为了能够对特殊环境中的突发状况作出快速反应,机器人与控制台接收端或其他机器人接收端必须正确恢复发送端的符号信息,这就要求信息的收发端做到定时同步。
自1993年Floyd M.Gardner提出了插值滤波器的速率转换模型以来,各类接收机的同步定时技术得到了空前的发展。
基于Gardner算法的定时同步模型,主要由插值滤波器、定时误差检测器、环路滤波器、数控振荡器(numerical controlled oscillator,NCO)组成[6-7],采用开环结构方式实现符号的定时同步。基于Gardner算法的定时同步模型结构如图1所示。

图1 基于Gardner算法的定时同步模型结构
1.1 插值滤波器
在Gardner定时恢复算法[6]中,插值滤波器的主要作用是通过输入信号x(mTs)、采样点mk和分数插值点uk来实时生成与本地时钟相位相同的信号。插值滤波器输入信号x(mTs)与输出信号y(kTi)的关系可表示为:
y(kTi)=y[(mk+uk)Ts]=
(1)
式中:I1、I2为决定插值滤波器的抽头系数;hI为插值滤波器的冲激响应;Ts为接收机的采样周期;k为一小整数。
设T为信号的符号周期,由于Ti与T是同步的,所以Ti=T/k。mk、uk由数控振荡器(NCO)提供,mk决定内插器的整数倍插值位置,uk控制小数倍插值位置,mk和uk共同决定插值点的位置。插值滤波器的实质是对信号经过低通滤波器后再重采样的过程。根据Shannon定理,由输入信号x(t)的抽样值x(mTs)精确得到内插后的序列x(kTi),可表示为:
(2)
由于理想的内插滤波器是非因果系统,它需要无穷多个信号样值点,物理上具有不可实现性。因此,对理想插值滤波器的脉冲响应进行截断,并根据最优化准则逼近最佳性能。本文选用基于4点样值拉格朗日函数的立方滤波器,其表达式如下。
(3)
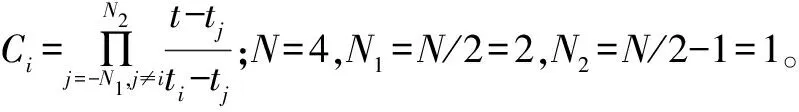
立方插值滤波器的时域表达式为:
1.2 定时误差检测器设计
定时误差检测器采用一种非数据辅助的误差检测算法——Gardner定时误差检测算法[7]。内插后的信号中每个符号需要两个重采样点,其中一个对应信号的最佳采样点,另一个为最佳采样点中间时刻的内插值。定时误差计算公式为:
τ(n)=y(n-1/2)×[y(n)-y(n-1)]
(4)
式中:τ(n)为定时误差检测值;y(n)为信号的采样值;n为第n个符号;Ti为输出信号的周期。
1.3 LPF和NCO设计
在机器人信息接收端,定时同步环路和频偏纠正模块都选择使用有源比例积分滤波器[8-9]。将模拟域上的传递函数使用双线性变换法变换数字域,然后进行反变换,可以得到离散时低通滤波器(low pass filter,LPF)递归方程[10]:
y(n)=y(n-1)+C1[x(n)-x(n-1)]+C2x(n)
(5)

一般情况下,fτ2=2fξ/ωn>>0.5,f为采样频率。
由定时误差检测器得到的定时误差经LPF后能够得到数控整荡器(NCO)控制字,通过调节环路滤波器系数查看接收机接收到的星座图,使整个环路能够工作在最佳性能时刻。
NCO时钟周期和接收机对输入信号采样周期同步,均为Ts;而内插器输出插值估计值周期与输入信号符号周期同步,即T=Ti。当NCO过零时,NCO对内插器输出一个内插时钟,同时提供插值基点mk和计算出分数间隔uk,控制内插器在适当位置完成插值运算,并且在插值基点的下一时刻,对NCO的值进行更新。
根据NCO计算原理[9],假设NCO的寄存器深度为1,mkTs时刻的寄存器值为η(mk),LPF输出值为e(mk),则可以求出分数时间间隔uk。
uk的计算公式为:
(6)
2 减小定时抖动方法
虽然Gardner定时恢复算法在实现位同步后,小数插值点uk将稳定于一个固定的波形上,但实际信号是在加性高斯白噪声信道(additive white Gaussian noise,AWGN)中传输。uk将沿着固定波形上下随机变化,这个变化称为定时抖动。定时抖动主要是因为输入信号中叠加有噪声。如果在环路中乘以一个小于1的环路系数,其他参数不变,则改变环路中的噪声系数,就可以减小定时抖动。
在定时恢复环路中,设通过NCO中输入频率控制字倒数为ε,将ε与当前相位累加器值η(mk)相乘,可求出小数插值点uk的表达式:
uk=εη(mk)
(7)
当信道中存在噪声,即ε=ε0+Δε+n0,ε0≈Ti/Ts,Δε为经环路滤波器后的误差输出值,n0为NCO输入噪声,实现定时恢复后Δε=0,则ε=ε+n0。
将ε代入式(7)得:
uk=(ε0+n0)η(mk)=ε0η(mk)+n0η(mk)
(8)
式中:ε0η(mk)为无噪声情况下的uk值;n0η(mk)为噪声项,为引起机器人数据接收端定时抖动的原因。
由式(8)可知,减小n0值,可在不影响定时恢复条件下减小定时抖动。根据数控振荡器中小数间隔uk与相位累加器几何关系,可得出NCO通过零点产生uk时刻相位累加器值为:
(9)
式中:η(0)为相位累加器初始时刻值。
无噪声情况下,η(mk)值只与初始时刻相位累加器值和累加次数有关。
将式(9)代入式(8)可以得出uk:
当输入信号的符号速率T与本地时钟周期Ts确定后,ε0为定值,η(0)也为定值。因而,通过减小输入NCO中噪声n0幅值,就可减小输出uk定时抖动。当无噪声时,符号同步后的定时误差检测器输出和环路滤波器输出均为0;当存在噪声时,环路滤波器输出则为噪声信号,即引起定时抖动的来源。所以在环路滤波器输出后,NCO输入前加入一个小于1的环路系数,使之与LPF输出相乘,则输入NCO中的噪声将会减小,从而达到减小定时抖动的目的。
3 仿真分析
为了得到一个合理的环路系数值,必须先分析环路系数对uk方差(即定时抖动大小)和实现定时恢复所需点数的影响。环路系数、uk方差和定时恢复点数3个参量间的关系如图2所示。由图2可以看出,uk定时抖动随着环路系数增加而逐渐增大,但系统定时恢复点数却随着系数增大逐渐减小。所以,环路系数并不是越大越好,具体值的选取要综合考虑环路系数、uk方差和定时恢复点数这3个参量相互之间的关系。根据图2的曲线变化趋势,可以得出环路系数取值范围为0.1~0.3时,uk的方差曲线和定时恢复点数存在交集。在该范围内,定时抖动与定时恢复点数均能取得一个较好的值,且能保证在uk的方差取得较小值时获得良好的定时恢复点数。

图2 环路系数、uk方差和定时恢复点数关系图
通过分析图2可以看出,环路系数大小的选择也并不是越小越好,因为在机器人数据接收端的定时恢复阶段,环路滤波器输出误差信号也与环路系数相乘,将影响数控振荡器(NCO)中mk、uk的调整速度,进而影响整个定时恢复速度。
在添加0.1环路系数前后uk的输出波形如图3所示。从图3能够直观地看出,在添加了环路系数之后,机器人数据接收端定时同步的恢复速度发生变化。
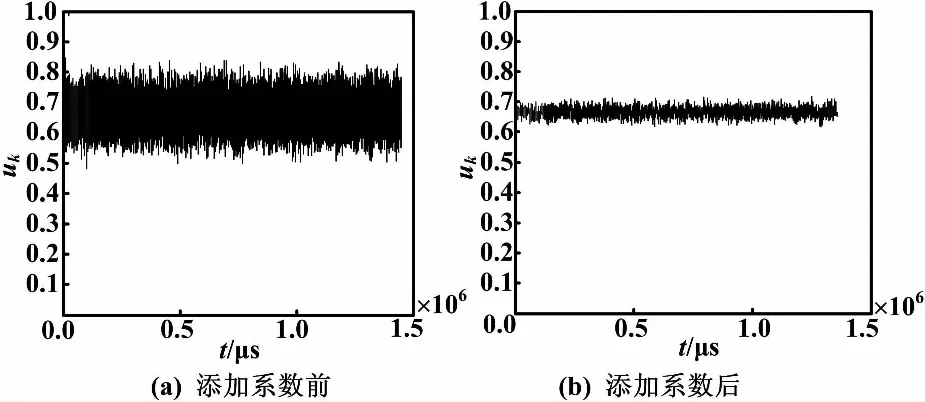
图3 添加系数前后uk输出波形
由图3可以看出,通过增加环路系数可以达到减小定时抖动的效果。
针对此定时恢复环路,采用蒙特卡罗法可以得到在有无环路系数两种情况下误码率和输入信噪比的影响关系,如图4所示。
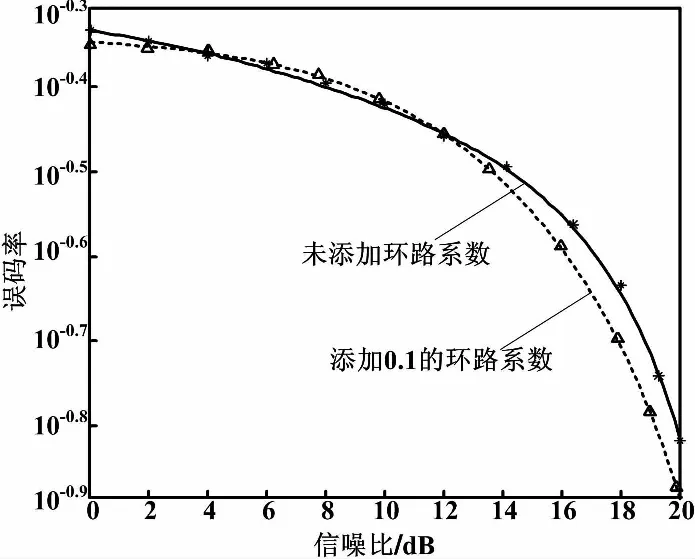
图4 误码率与输入信噪比关系图
在分析无线通信系统的定时同步环路中,数控振荡器的uk方差作为整个同步系统的一个重要参考指标,因此通过观察uk的方差与输入信噪比的关系,可以验证添加环路系数的方法对整个定时同步环路的影响。在数控振荡器添加和不添加0.1的环路系数时,通过试验记录的输入信噪比与uk方差关系如表1所示。

表1 输入信噪比与uk方差关系
4 结束语
为了解决远程机器人在特殊环境中通过无线通信系统协调完成作业任务时同步系统中存在的定时抖动问题,本文开展了多机器人在采用GSM/GPRS无线通信方式时数据接收端涉及到的同步技术研究。通过对基于Gardner定时同步算法模型的仿真分析研究,提出了一种用于机器人数据接收端同步系统中减小定时抖动的方法,并在Matlab环境下进行了仿真分析。仿真试验结果表明,该方法能够有效地抑制同步系统中的定时抖动问题,提高了机器人接收信息端同步系统的稳定性。
[1] 杨茂,李成凤,田彦涛.动态环境下群体机器人同步的分布式控制[J].吉林大学学报:自然科学版,2011,41(2):497-502.
[2] 吴楠,郭培源,陈岩,等.基于嵌入式Linux的GPRS机器人通信系统研究[J].机器人技术与应用,2007,16(5):37-40.
[3] Simon M,Tkacenko A.Noncoherent data transition tracking loops for symbol synchronization in digital communications[J].IEEE Transactions on Communications,2006,54(5):760-760.
[4] 刘祖军,王杰令,易克初.一种采用匹配滤波器插值的符号定时同步方法[J].西安交通大学学报:自然科学版,2008,42(12):1550-1554.
[5] Mueller K,Muller M.Timing recovery in digital synchronous data receivers[J].IEEE Transactions on Communications,1976,24(5):516-531.
[6] Gardner M.Interpolation in digital modems-Part I:fundamentals[J].IEEE Transactions on Communications,1993,41(3):501-507.
[7] 付永明,朱江,琚瑛珏.Gardner定时同步环路参数设计及性能分析[J].通信学报,2012,33(6):191-197.
[8] Candan C.An efficient filtering structure for Lagrange interpolation[J].IEEE Signal Processing Letters,2007,14(1):17-19.
[9] 刘顺兰,赵晓菲.SC-FDE系统中改进的粗定时同步技术[J].计算机工程,2011,37(10):105-107.
[10]Harris F J,Rice M.Multirate digital filters for symbol timing synchronization in software defined radios[J].IEEE Journal on Selected Areas in Communications,2001,19(12):2346-2357.
