EMD边缘效应问题的一种处理方法

滕建方，王 俊，李 维

（中航工业洪都，江西南昌330024）

0 引言

HHT方法是近几年成功应用故障诊断的一个新的方法，其核心是EMD。该方法由Huang于1998年提出，具有自适应特性,适宜于非平稳信号的分解[1,2]。因为实际故障诊断信号几乎都是非平稳信号，所以，准确的分析处理非平稳信号是故障诊断成功与否的关键。而如今EMD分解一般采用的是三次样条插值的方法，对于有限长信号而言，将不可避免的带来边缘效应的问题。Huang指出该问题可在信号的两端，根据端点信号的振幅和频率，分别加两个特征波来解决，但没有给出具体的做法；事实上，他们的方法已向美国宙航局申请了专利.并称该问题仍然没有彻底解决，由此可见，边缘效应问题是EMD的一个重要的亟待探讨和完善的问题。

1 EMD信号分解方法介绍

EMD方法的大体思路是用波动上、下包络的平均值去确定“瞬时平衡位置”,进而提取固有模态函数IMF。IMF要满足两个条件：1)整个数据集的极大极小值数目与过零点数目相等或最多相差一个；2)数据集的任意点上，由极大值确定的包络与由极小值确定的包络的均值始终为零。这两个条件实际上使得分解得到IMF是窄带信号。而且EMD分解基于下面的假设：1)信号至少有两个极值，一个极大值和一个极小值；2)信号特征时间尺度是由极值间的时间间隔确定的；3)如果数据中缺乏极值点，但存在缺陷点，可通过微分、分解、再积分的方法获得IMF。EMD具体分解过程如下：

对任一信号x(t)，首先确认x(t)上的所有极点，然后将所有极大值点和所有的极小值点分别用三次样条插值形成的曲线连接起来，使两条曲线包含所有的信号数据，从而得到x(t)的上、下两条包络线，若两条包络线的平均值记作m，将x(t)与m的差记作h，即：x (t)-m=h，视h为新的x(t)，重复以上操作，直到h满足一定的条件时，记c1=h。c1视为一个IMF，x(t)-c1=r，将r视为新的x(t)，重复以上过程，依次得第二个IMF，第三个IMF，直到cn或r满足给定的终止条件。由此可得x(t)的分解式：

其中，r为残余函数，代表信号的平均趋势。

2 EMD边缘效应问题

EMD边缘效应问题的本质是由于三次样条插值带来的。一般说来，三次样条插值方法对信号以外的插值点的插值只是边界点处相邻二点的三次多项式的延伸.而由于现实信号的多样性，三次样条插值方法很难保证端点外的插值精度，而EMD变换恰恰需要对信号的全部极大值和极小值点进行插值，则一定会出现端点外插值的情况，因而出现端点效应是不可避免的。而在端点处不是极值点的情况进行三次样条插值时，必然会使得信号的上下包络在信号的两端附近严重扭曲。在信号的高频分量，由于时间尺度小，极值间的距离小，端部的边缘效应仅局限在信号两端很小的部分。但对于低频分量，由于其时间尺度大，极值间的距离大，端部的边缘效应就传播到信号的内部，特别是原始信号数据集比较短时，会严重影响EMD分解的质量，使得分解出来的IMF分量没有实际的物理意义。

现在解决该问题的思路一般是两种：一种是改进或者替换三次样条插值的方法，如采用约束三次样条插值；另一种是仍然利用三次样条插值而依据信号本身的特征进行某种处理，如对信号进行延拓，在每次平滑过程中根据信号的特征在两端点处添加极值点等。如今的解决方法一般是第二种思路，其中最成功的莫过于镜像法，无论在效率还是效果上，镜像法都处于一个较高的水平上，是现如今应对边缘效应问题上极佳的选择。但尽管如此，镜像法也有很多不足的地方，其中一个重要的问题是镜像方法对边缘处的信号依赖性大，当端点处无法确定为极值点时常会带来端点漂移现象，引起振荡误差。

当然镜像法可以由人来根据信号的特征来确定镜子的位置，但这也就造成对人的依赖因素过大，而且对于实时系统与随机性比较强的信号显然无法行的通，另外在非端点处安放镜子的位置也需丢弃边缘处真实的信号，这对于数据集比较短的信号无疑会影响处理效果。本文提出的算法就是在镜像方法的思想上利用边缘数据添加极值点的方法，来减少三次样条插值带来的边缘效应。

3 利用边缘数据添加极值点的新方法

本文方法的基本思想是在每次的平滑过程中，在边界处合适的位置，利用边缘信号某切点处的切线与y轴的交点来确定添加的极值点，再在以极值点处为对称轴向两端扩展从而得到所需的新极值点，具体措施如下：

1）极值点位置的确定

对于原始信号，首先判断两端边缘处的数据是否可取，对于过短的数据（如少于前三个极值点距离平均值的一半）则丢弃，以第一个极值点作为镜子的位置，对于较长的数据（大于前三个极值点距离的平均值）则直接以端点处作为镜子的位置，而对于两者之间的情况则以第一个极值点向外一个平均值的距离作为镜子的安放处。安放镜子之后就可以利用原信号的极值点对称的拓展新的极值点。

2）极值点值的确定

当信号边缘处数据过短，直接以信号本身极值点作为镜子的位置时可以以镜像方法的思想来获取添加的极值点，但对于1）中后两种情况，则按照以下方法进行。具体方法是：假设信号第一个极值点为极大值点，取其起点与第一个极值点中间的信号求导，确定其求导后的最大值k，及最大值k所在的切点的位置(x,y)，以方程y=k*x+b来确定b，而b就是所要添加的极小值。一般情况下，b值能很好的体现边缘处信号的趋势，接近于真实的极值点，个别情况下可能会超过信号的最值点，这种情况下则以最值点来代替b值。其他情况与其类似，只不过确定是最小值k，添加的是极大值而已。末端信号数据的处理也与其雷同。

在新的极值点处安放镜子拓展极值点 （一般扩展四到五个即可），利用新的极值点集进行三次插值，从而得到原信号的上下包络线。余下过程按照正常EMD程序处理。

该方法是充分利用边缘处信号的特征，即边缘数据某切点处的切线与y轴的交点来添加端点附近所需的极值点，再加上利用镜像方法的思想拓展所需的其它极值点，所以可称为切点方法。该方法能较好适应端点非极值点的情况，对信号的适应性更强，提高了处理效果，能很好的抑制边缘效应。

4 算例分析

本文采用如下算例进行验证：

1）算例1：

采样频率取200Hz，时间取0.3-2.25秒，理论上各阶IMF分量由高到低分别是8Hz，4Hz，1Hz，以下为镜像方法，本文方法EMD分解后得到的各阶分量与真实IMF分量的对比。

从图1、图2和图3中可以看出，本文方法有效的抑制了三次样条插值带来的边缘效应，比之镜像方法得到的各阶IMF分量都有明显改善，特别是随着分解的继续，镜像方法的低阶分量前端数据已经与真实分量有较大的差距，而本文的方法不但在高阶分量上很好的体现了真实分量，也在低阶分量上有较好的表现，并且各阶分量在末端上也很好的保留了镜像方法的优势。

2)算例2：

所产生的原始信号如图4所示。

镜像方法分解产生了多达11阶IMF分量与一个残余量，其中仅有头两阶可取，头两阶IMF如图5、图6所示。

从分解结果来看，镜像方法虽然如实的反映了真实的IMF分量，但是引进了多余的IMF分量，而本文方法从效果上看比之镜像方法略好，且没有多余的IMF分量。

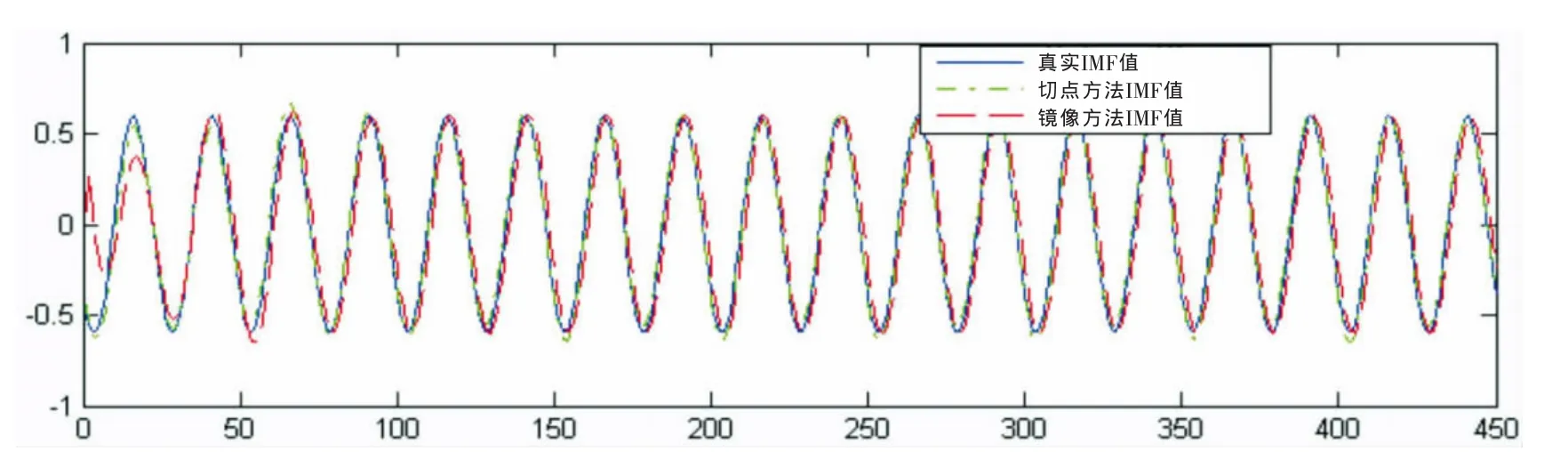
图1 算例1第一阶IMF分量对比

图2 算例1第二阶IMF分量对比

图3 算例1第三阶IMF分量对比

图4 算例2原始信号

图5 算例2第一阶IMF分量对比

图6 算例2第二阶IMF分量对比

5 结论

本文将镜像方法的思想与普通添加极值点方法结合，并利用了边缘信号的切线与y轴的交点来添加极值点，有效的抑制了边缘效应，分析结果表明：

1）该方法继承了镜像方法的优点，并且以边缘信号的切线与y轴的交点来添加新极值点的方式，很好的弥补了镜像方法对信号适应性差的缺陷，减少了因为端点非极值点而带来的振荡误差，使得处理效果更加完善。

2）本文采用的思想是镜像思想，而实际程序运行则是一般添加极值点的方法，效果上比镜像方法更好，适应性更强，因为无须延拓信号本身，所以处理时间上也要高效很多。

[1]Huang NE，Shen Z，Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non—stationary time series analysis[J] Proc R Soc Lond A,1998,454：903-995.

[2]Huang NE，Shen Z，Long S R.A new view of non— linear water waves：the Hilbert spectrum[J]. Annual Review of Fluid Mechanics,1999,31:417-457.

[3]邓拥军，等.EMD方法及Hilbert变换中边界问题的处理[J].科学通报，2001，46(3)：257-263.

[4]黄大吉,赵进平,苏纪兰.希尔伯特—黄变换的端点延拓[J].海洋学报,2003,25(1):1-11.

[5]舒忠平,杨智春.抑制经验模分解边缘效应的极值点对称延拓法[J].西北工业大学学报,2006,24(5): 639-642.

[6]陈忠,郑时雄.EMD信号分析方法边缘效应的分析[J].数据采集与处理,2003,18(3):114-118.

[7]许宝杰，张建民，徐小力，李建伟.抑制EMD端点效应方法的研究 [J].北京理工大学学报，2006，3：196-199.