我国高校专利分类变化的评价模型及其回归分析*

2014-04-02谢雨飞朱周力翟晓亮李静玉

技术与创新管理 2014年3期

谢雨飞，朱周力，翟晓亮，马琳，李静玉，朱平

(1.江南大学物联网工程学院，江苏无锡214122;2.江南大学理学院，江苏无锡214122)

随着我国高校专利申请数量的不断增长，发明专利，实用新型专利以及外观设计专利在专利申请总量上所占的比重有明显的变化。因此我们需要找到影响专利申请数量的关键因素，并据此建立一个科学、合理、有效的数学模型，该模型能够很好的拟合历年的专利申请数据，并且可以较准确地预测未来专利申请数量的变化趋势，从而能够通过改变某一影响因素实现在特定时期内控制专利申请的总量以及不同种类专利申请量之间的比例关系。

在信息技术高速发展的今天，集成化的专利文献信息资源以网络化为依托，实现了专利文献的数字化、网络化，从而拓宽了专利文献信息的渠道，加强了专利文献信息的传播和利用。将这些专利信息进行收集、整理、分析所制成的专利地图以及专利数量回归模型将在我国高校专利分析中扮演重要的角色。

1 研究方法和数据

专利申请量与专利授权量均能在一定程度上说明我国高校的专利产出水平，但是由于专利授权量受到政府专利机构等人为因素的影响较大，使得专利授权量由于不确定因素增大而容易出现异常变动，所以本文选择专利申请量作为分析与预测的研究对象[1]。目前能够影响高校专利申请量的因素有很多，涉及到国家宏观政策、科技人力、科技经费、科技机构、科技项目、科技成果及技术转让等众多方面。

1.1 样本的选择和数据的采集

我国《专利法》明确规定，专利有发明、实用新型和外观设计三种类型[2]。发明，是指对产品、方法或者其改进所提出的新的技术方案;实用新型，是指对产品的形状、构造或者其结合所提出的适于实用的新的技术方案;外观设计，是指对产品的形状、图案或者其结合以及色彩与形状、图案的结合所做出的富有美感并适于工业应用的新设计。因此，从专利的定义和种类来看，中国高校人文社科类专业的研究与专利的相关度不大，本文在研究的过程中只考虑理、工、农、医类专业的相关研究。

专利法》经过第二次修正(2000年)之后，不仅加大了专利保护力度，完善司法和行政执法，还简化、完善了专利审批和维权程序，维护当事人的合法权益。这些因素都将影响我国高校专利申请量的变化，因此本文主要选取了2001—2011年全国设有理、工、农、医类教学专业的高等学校及其附属医院在基础研究、应用研究、试验发展、以及R＆D(科学研究与发展)成果应用、其他科技服务、科技成果转让等各个层面开展研究的总体数据。选取的数据时间跨度为11年，主要涉及科技人力、科技经费、科技机构、科技项目、科技成果及技术转让等情况，共有143组数据。

本文研究的数据主要来源于《2002—2012年高等学校科技统计资料汇编》[3]。《汇编》是教育部科学技术司根据国家的统一部署和高等学校科技工作的具体情况，在组织各省、自治区、直辖市教育厅实施“全国普通高等学校科技统计年报(理、工、农、医)”的基础上，经过综合加工、整理而成的全面反映高等学校科技活动总体状况的数据资料汇集。此外，其他数据取自《2002—2012年中国统计年鉴》[4]和《2002—2012 年中国科技统计年鉴》[5]。最终2001—2011年我国高等院校专利申请量及其影响因素的统计结果见表1。

表1 2001—2011年我国高等院校专利申请量及其影响因素

1.2 研究思路和方法

文章研究思路和方法主要包括:

1)利用Multi-Agent技术绘制出专利地图，分析我国各地区高校专利申请量的情况;

2)将2001—2010年的数据作为训练样本，利用逐步回归的分析方法从中筛选出影响程度较高的因素，构建多元线性回归分析与预测模型，最后根据2011年影响因素的值对该年的研究对象的值进行预测，并与2011年研究对象的实际值进行比较，计算出预测相对误差并进行修正，使模型具有相对准确的预测性能。

2 专利地图、Multi-Agent系统以及多元线性回归的概念

2.1 专利地图

专利地图(Patent Map)[6]是将各种与专利相关的资讯信息，以统计分析的方法，加以缜密及精细剖析整理制成各种可分析解读的图表信息，使其具有类似地图指向功能的形象称呼。采用计算机技术之后，专利地图可以重新概括定义为专利信息图形化处理和专利数据的系统管理方法。

专利地图一般可以分为专利管理地图和专利技术地图。专利管理地图主要包括:历年专利件数动向图、申请人分布图、所属国专利数量比例图、企业发明阵容比较图、专利研发经费比较图等。在专利管理地图的基础上，找出主要的专利文献，并且对这些主要文献进一步地解读，得到这些专利文献的技术目的，采用的技术手段及所要达到的技术功效，就可以开始专利技术地图的绘制。专利技术地图主要包括专利引证关系技术族谱图、专利技术/功效矩阵图、专利技术发展图等。专利技术地图一旦完成，我们可以清楚地看出特定技术的动向，并进一步预测技术的未来趋势。

2.2 Multi-Agent系统

Agent技术[8]属于人工智能的范畴，具有以下特征的软件实体:①自治性(Autonomy):即Agent能根据外界环境的变化，而自动地对自己的行为和状态进行调整，而不是仅仅被动地接受外界的刺激，具有自我管理自我调节的能力。②反应性(Reactive):Agent能对外界的刺激做出反应的能力。③主动性(Proactive):对于外界环境的改变，Agent能主动采取活动的能力。④社会性(Social):Agent具有与其它Agent或人进行合作的能力，不同的Agent可根据各自的意图与其它Agent进行交互，以达到解决问题的目的。⑤进化性(Evolutionary):Agent能积累或学习经验和知识，并修改自己的行为以适应新环境。

Multi-Agent系统[9]是多个 Agent组成的集合，其多个Agent成员之间相互协调，相互服务，共同完成一个任务。它的目标是将大而复杂的系统建设成小的、彼此互相通信和协调的，易于管理的系统。基于DAI技术的Multi-Agent系统，就是通过分布式的智能Agent之间的交互、协调和沟通来处理分布式问题，从而克服传统的人工智能所建立的单一的、独立的系统所不可避免的缺陷。

Multi-Agent系统之所以可以应用到专利地图中，就在于该系统的特点能够适应专利地图的要求。专利地图的本质就是专利信息的集合，因此制作专利地图的关键就是收集和处理信息，从而为我国高校调控专利申请的数量与分类比例提供决策支持。单个的Agent就相当于一个信息处理器。因此，当出现一种新的信息处理方法，就可以简单地创建一个新的Agent，然后把它部署到原系统中，从而使得系统具有很好的扩展性。

专利文献是专利地图信息的主要来源，通过有关专利检索数据库就可以获得信息资源。最初的检索结果和获得的文献量可能非常大，这些文献必须依靠人工来进行浏览和筛选，剔除与制作专利地图需求无关的部分，得到与研究内容相关的专利文献，利用筛选后的专利文献进行专利管理图的制作。在专利管理图的基础上，找出主要专利文献，并对这些主要专利文献进一步解读，得到这些专利文献的技术目的、采用的技术手段及所要达到的技术功效，就可以开始专利技术图的制作。也就是说，制作专利地图所使用的信息资源结构通常比较复杂，包含结构化信息和非结构化信息。Multi-Agent System则通过人类Agent和机器Agent的设计理念，成为最能实现人机合作的系统模型。

2.3 多元线性回归

多元线性回归分析[11]是一种用于研究一个随机变量或因变量Y与一个或多个自变量(X1～Xn)之间的相互依存关系，并利用统计分析方法和函数对这种关系的实质、特点、变化规律等进行分析解读和形式化描述的方法。具有方法简单，对变量之间关系解释能力强的优点，在社会、经济、技术以及众多自然科学领域有着广泛的应用。

多元线性回归分析模型的形式化描述如公式(1)所示:

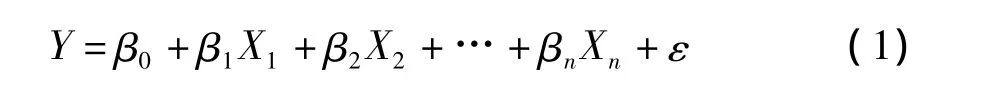
其中β0是常数项，表示当所有自变量为0时因变量Y的总体平均估计值;β1～βn表示回归系数，主要有两种:标准化回归系数和非标准化回归系数[12]。β1表示除X1之外的其它自变量固定不变的情况下，X1每改变一个测量单位时所引起的因变量Y的平均改变量，β2n表示意义与β1一样。ε是被称为误差项的随机变量，它说明了包含在Y里面但不能被n个自变量的线性关系所解释的变异性。

多元线性回归分析模型的构建主要通过各种回归分析方式将一些有效的，对因变量影响显著的自变量加入到回归模型中，然后对模型进行各种检验，主要包括判定系数检验(R检验)、回归系数显著性检验(T检验)、回归方程显著性检验(F检验)[13]。检验通过，该分析模型构建完成。

3 基于Multi-Agent系统的专利地图的制作

3.1 基于Multi-Agent系统的专利地图设计

如图1所示的Multi-Agent系统中，人类专家可以通过智能界面Agent与机器Agent进行信息交换和沟通，实现人机合作的关键是智能人机界面A-gent的存在[14]。

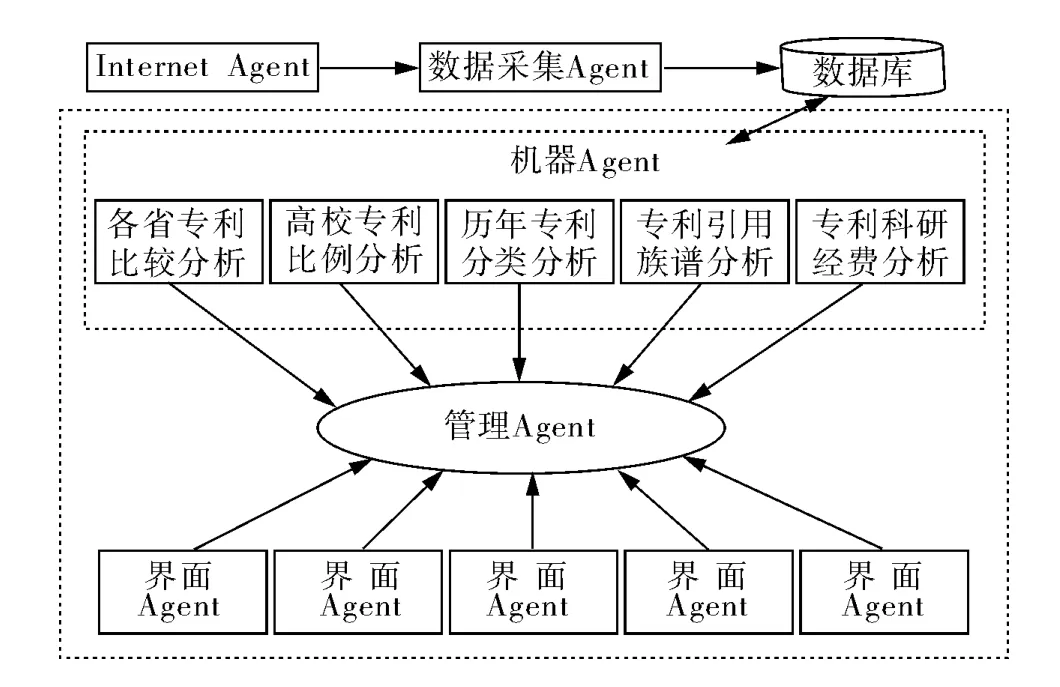
图1 基于Multi-Agent的专利地图示意图

1)Internet Agent模型:Internet Agent就是网络中的任一网站，无需本系统的干预;

2)数据采集Agent模型:通过网络在有偿或无偿提供的专利数据库中检索我国高校专利情报，同时将搜集到的专利情况进行标准化处理，做代码化的技术分类，使其数据库化。该模块能够对特定的网站进行实时监控，当有关键数据发生变动时，能够自动地执行相关操作;

3)机器Agent模块:这类模块主要是对数据库中的专利信息进行专利分析，分析是基于专利分析理论及数理统计分析理论的基础之上的。鉴于前文提到的专利地图的分类，我们可以建立起历年专利动向分析Agent、高校专利占有比例 Agent、历年专利分类分析 Agent、专利引用族谱分析 Agent、专利研发人员分析Agent、专利科研经费分析 Agent、专利成果转让分析Agent、专利研究机构分析Agent等;

4)管理 Agent模块[15]:它是系统的核心，是一个功能完整的独立模块，负责多个Agent之间的协调控制及各个Agent的路径信息的存储和查询。本系统由于协作任务量不大，整个系统采用集中式的控制方式;

5)界面Agent模块:这类模块主要是对机器A-gent的分析结果进行可视化，鉴于专利地图分析的复杂性，界面Agent综合考虑了机器Agent的分析结果和专家分析的结果。界面Agent的存在综合了非结构化决策和结构化决策模型的优点，提高了决策的准确性。

3.2 专利地图实例

根据上述的系统分析过程，设计了多个基于Multi-Agent专利地图原型系统。此处以江南大学的专利申请量和全国所有高校的专利申请量为例，即选取江南大学2011年专利申请数量和全国高校2011年专利申请数量为研究对象，研究各个种类的专利占有比例，经数据收集Agent和高校专利比例分析Agent处理后得到的关键数据见表2，表3。

表2 2011年江南大学各种专利申请数量

表3 2011年全国高校各种专利申请数量

界面Agent从表2获得数据，然后可视化表示如图2所示。

界面Agent从表3获得数据，然后可视化表示如图3所示。

从图中我们可以明显地看出江南大学外观设计专利所占比重较大，远远超过全国高校外观设计专利所占的比重，而发明专利所占的比重则几乎只有全国高校发明专利所占比重的一半，由此我们可以看到:江南大学在专利方面存在申请总量大，创新性不强，分类比例极端不合理等问题，因此，建议首先可采取政策调控等手段加大对发明专利和实用新型专利的奖励力度，设立专利维持基金。其次可以通过科学论证的方法有选择性地保护一些重点核心专利。此外，还可以加强产学研合作，让高校专利在市场中应用并加以实施，真正发挥其价值。当然我们也可以推广到其他学校也可能存在着各种专利所占比例不尽相同，与全国高校总体情况存在较大差异的现象。

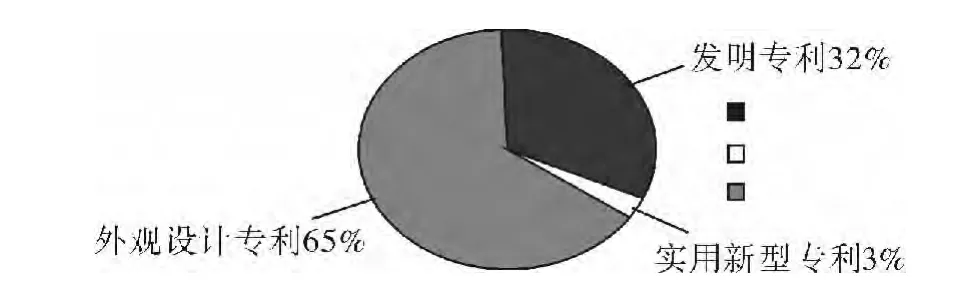
图2 2011年江南大学专利申请种类分布图

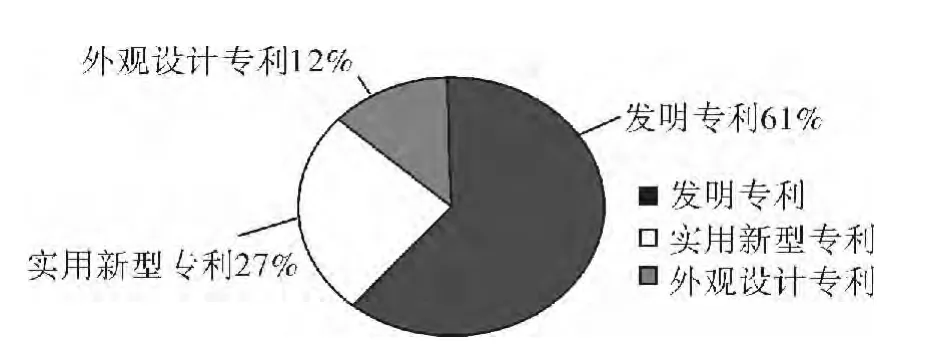
图3 2011年全国高校专利申请种类分布图

此外我们以全国各地区高校专利申请量为例，即选取全国各地区高校2011年专利申请数量为研究对象，经数据收集Agent和各省专利比较分析A-gent处理后得到的关键数据见表4。

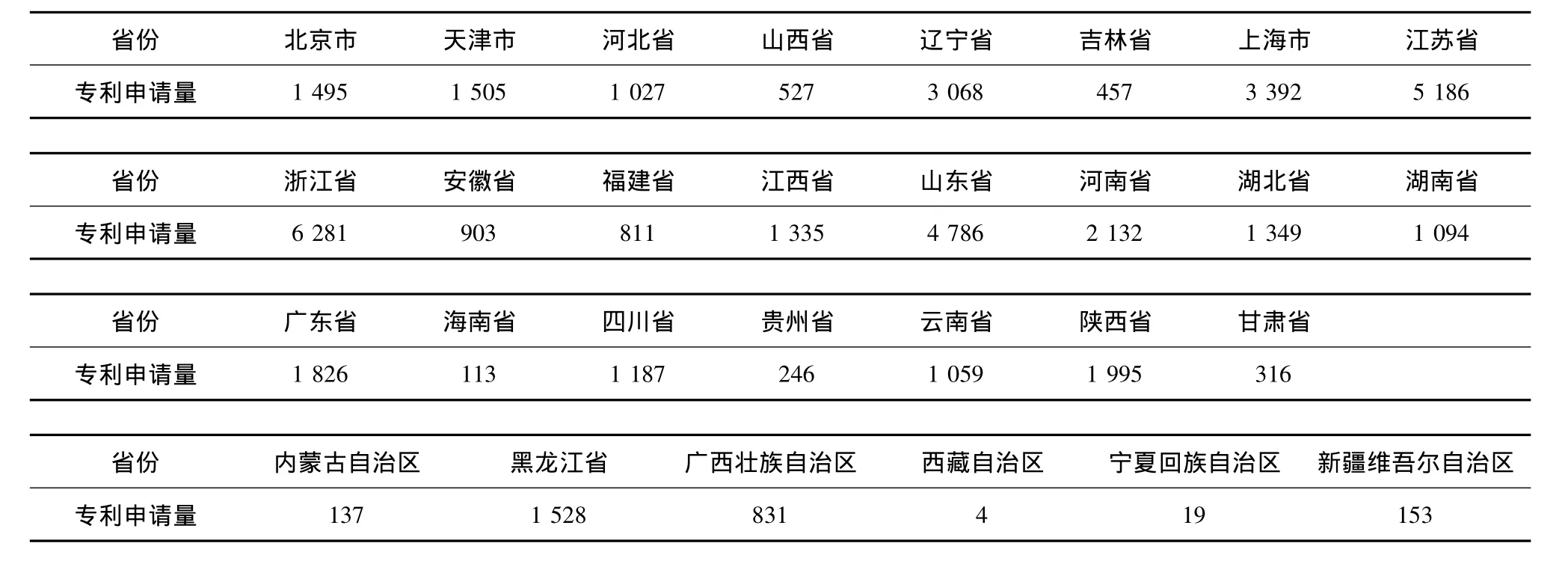
表4 2011年全国各地区高校专利申请数量

界面Agent从表4获得数据，然后可视化表示如图4所示。图中颜色的深浅反映出全国各地区高校的专利申请数量的多少，从图中我们可以直观地看出我国东南沿海一带地区高校专利申请量较多，中西部地区高校专利申请量较少，东西差距十分明显。

那么影响我国高校专利申请量以及分类变化的主要因素究竟是什么以及我们如何得出高校专利申请量的预测模型，本文在此基础上进行进一步的研究。

4 基于多元线性回归分析的我国高校专利申请量的预测模型

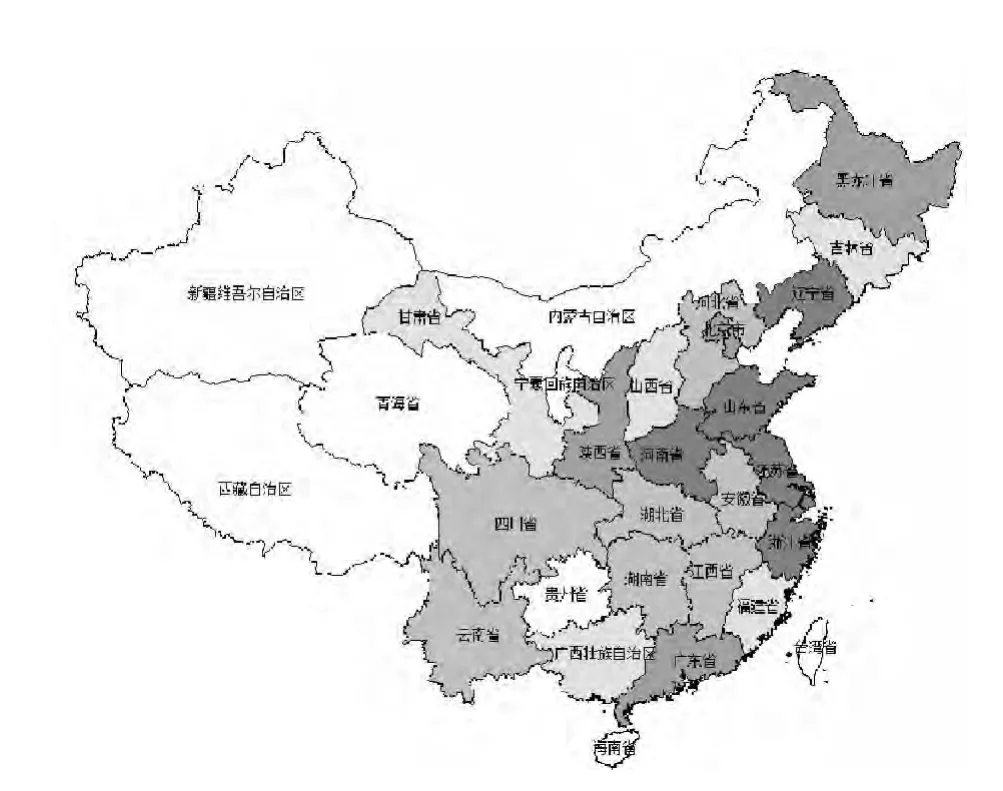
图4 2011年全国各地区高校专利申请地图

本文将发明专利申请量，实用新型专利申请量，外观设计专利申请量作为因变量即分析与预测的目标变量，标记为Y1、Y2和Y3。将各影响因素作为自变量，具体标记情况见表5，标记之后，我们利用多元线性回归分析方法通过SAS软件[16]分别对三个因变量与其自变量的关系进行回归分析，回归分析的结果见表6～表12所示(仅以发明专利为例)。

表5 各主要影响因素的具体标记情况

表6 所有因素在内的方差分析表

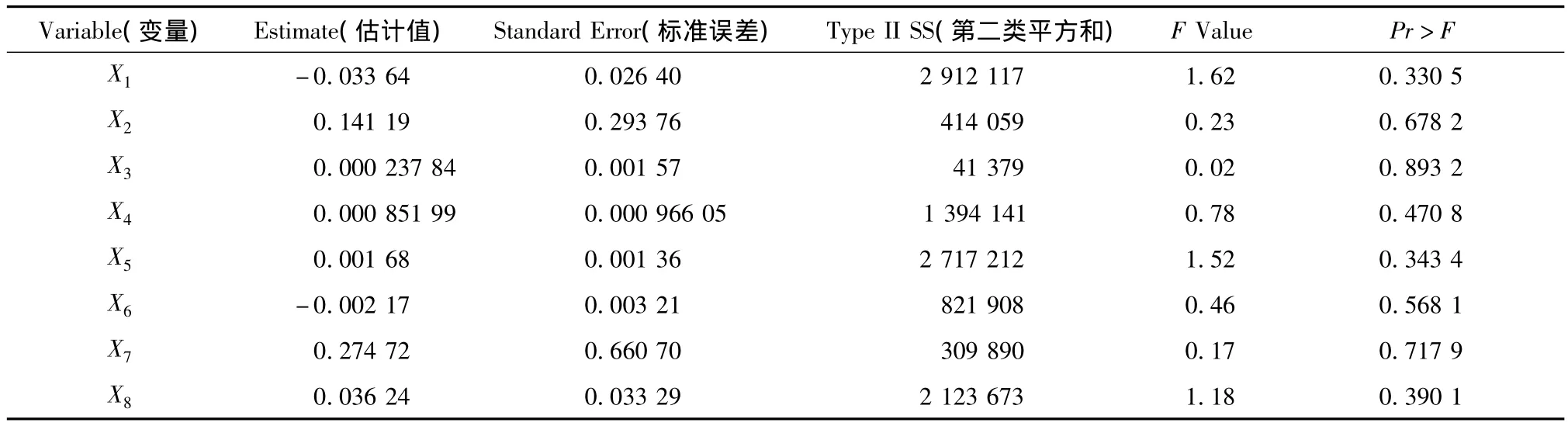
表7 所有因素在内的参数估计表

表8 逐步回归第一步后的方差分析表

表9 逐步回归第一步后的参数估计表

表10 逐步回归结束后的方差分析表

表11 逐步回归结束后的参数估计表

表12 逐步回归法剔除变量结果摘要

表6表示所有因素在内的回归模型的方差分析结果，其中F是检验方程显著性的统计量，是回归均方与剩余均方之比，其值越大越好[17]。Pr＞F称作P值，表示显著性水平，其值要求小于0.05或0.01，小于0.01 表示回归差异极显著，处于 0.01 和0.05之间表示回归差异显著。本次回归的P值为0.002 7，小于 0.01，表明回归差异极显著。

表7表示所有因素在内的参数估计表即回归分析的各项系数，其中P值均大于0.05，表明各影响因素之间可能存在较强的相关性，需要剔除其中显著性水平较弱的因素。由于基础研究经费(X3)的P值最大，故决定首先剔除基础研究经费(X3)因素。

表8表示剔除掉基础研究经费(X3)因素后的回归模型的方差分析结果，可以看出，F统计量的值变大，表明方程的显著性增强。P值小于0.000 1，表明回归差异极显著。

表9表示剔除掉基础研究经费(X3)因素后的参数估计表即回归分析的各项系数，可以看出，剩余各影响因素的P值均有所减小，显著性增强。其中应用研究经费(X4)的P值减小的最多，表明应用研究经费(X4)与基础研究经费(X3)之间有较强的相关性，并且应用研究经费(X4)对发明专利申请量的影响程度更大。

表10表示逐步回归结束之后的回归模型的方差分析结果，可以看出，F统计量的值再次变大，表明方程的显著性增强。P值小于0.000 1，表明回归差异是极其显著的。

表11表示逐步回归结束之后的剩余因素的参数估计表，所有因素中只有X1(教学与科研人员)，X4(应用研究经费)和X8(发表学术论文数)三个因素被选入到回归模型中。在多元回归分析中，能够选入回归模型的自变量都是对因变量即研究对象影响程度较大的变量，可以明显地看出最终留下的三个变量的P值均远远小于0.05，表明回归差异极显著。通过将表11中的回归系数带入构建的回归预测模型中，得到如下的发明专利申请量的回归分析预测方程:

表12表示逐步回归法剔除变量结果的摘要，其中R的平方称为判定系数，主要用于衡量回归模型的拟合优度或用来说明自变量解释因变量变异的程度。R方越大越好，一般地，大于0.8，说明方程对样本点的拟合效果很好。本次回归一共经过5步完成，最终模型的R2为0.998 1，表明最终方程对样本点的拟合效果很好。

通过MatLab编程[18]，我们可以得到发明专利样本点与回归方程的拟合图像，如图5所示(其中实线代表样本点的连线，虚线代表回归方程的图像)。

图5 发明专利样本点与回归方程的拟合图

同理我们可以得到实用新型专利与主要影响因素的线性回归方程:

通过MatLab编程我们可以得到实用新型专利样本点与回归方程的拟合图像，如图6所示:(其中实线代表样本点的连线，虚线代表回归方程的图像)

同样可以得到外观设计专利与主要影响因素的线性回归方程:

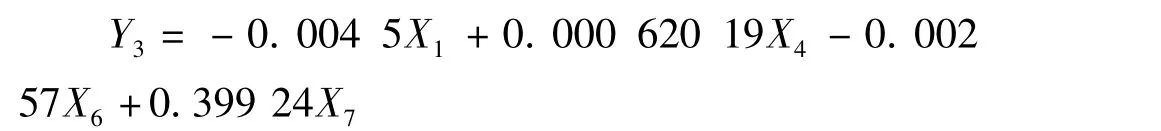
通过MatLab编程，我们可以得到外观设计专利样本点与回归方程的拟合图像，如图7所示:(其中实线代表样本点的连线，虚线代表回归方程的图像)

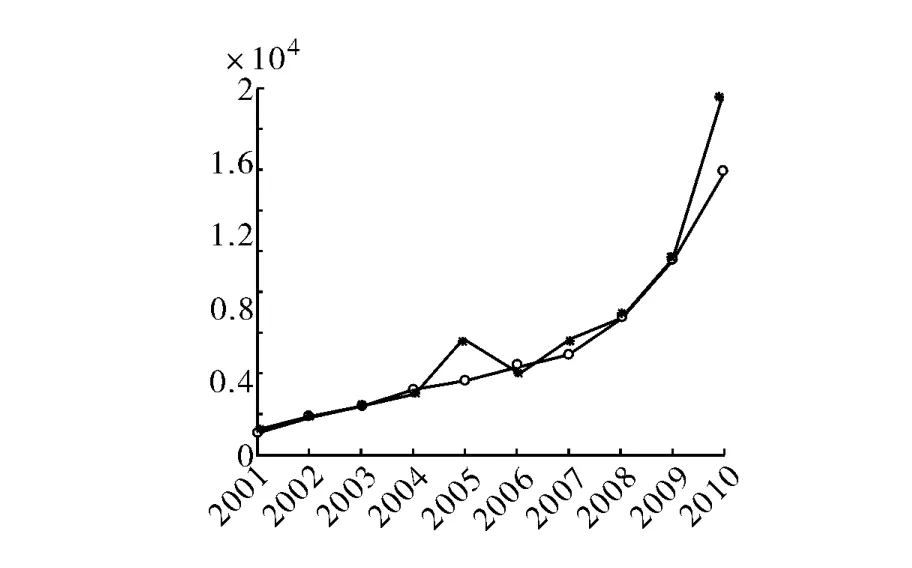
图6 实用新型专利样本点与回归方程的拟合图

图7 外观设计专利样本点与回归方程的拟合

从以上三个图中可以看出多元线性回归方程对样本点的拟合结果还是比较准确的，我们将2011年的数据带入以上三个预测方程中，从而能预测出三种不同专利类型的申请数量。预测结果与实际值的误差见表13。可以看出，除了发明专利以外，实用新型专利与外观设计专利预测相对误差较大。

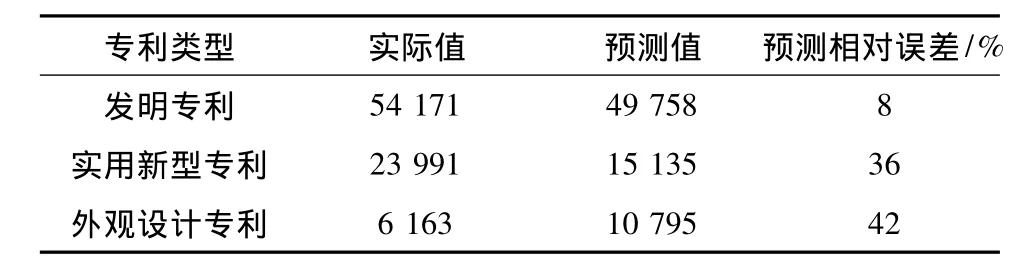
表13 2011年各种专利申请量的预测值及其与实际值的误差

5 结语

鉴于目前我国高校专利申请量影响因素分析与预测研究方面，不够系统全面，定性研究多，定量研究少，分析研究多，预测研究少的现状，融合Multi-Agent技术、多元线性回归分析预测方法，并用2011年的数据进行预测验证研究。研究结果表明:

1)对发明专利申请量影响较大的是教学与科研人员(X1)，应用研究经费(X4)，发表学术论文数(X8);对实用新型专利影响较大的是教学与科研人员(X1)，应用研究经费(X4)，R＆D成果应用经费(X6);对外观设计专利影响较大的是教学与科研人员(X1)，应用研究经费(X4)，R＆D成果应用经费(X6)，R＆D成果应用项目数(X7);

2)多元线性回归分析预测模型可以很好地拟合样本数据，具有很高的有效性。

针对以上研究结果，我们可以对国家专利发展战略提出如下建议:

①加大对教学与科研人员的培养，为国家源源不断的注入新鲜的血液;

②建立科学细致的经费管理体制，从根本上解决经费管理问题，让经费真正的应用到科研开发中，使其能够最大比例的转化为专利成果;

③建立关于科研工作科学性与严谨性要求的科技政策与法规，用以制约、监督检查和管理那些错误很多的科研课题、科研成果。同时加大对高校论文的重视，大学生具有丰富的创造力和想象力，加大大学生对科研兴趣的培养力度很重要，这将极大的提高学术论文的发表数量与质量。

由于影响专利申请的因素大概有20多种，而本文仅仅选择了其中的八个因素进行多元线性回归分析，所以得到的分析结果存在一定的不完全性。又由于2001年之前各因素的数据缺失比较大，2011年之后的各因素的数据也不全，因此在本文分析中仅选用了2001—2011年间的数据做分析与预测实证研究，数据的规模和历时性可能会对分析与预测的结果造成一定的影响。因此还需要进一步针对回归预测模型深入研究，给国家专利发展找略提供更为有效的建议和方案。

[1]翟东升，周娟，王明吉.基于多Agent的专利地图研究[J].情报杂志，2006(7):2－4.

[2]雷迪.专利地图在我国高校专利技术研发中的应用[J].科技管理研究，2011(6):175 －178.

[3]教育部科学技术司.高等学校科技统计资料汇编(2002－2012)[M].北京:高等教育出版社，2002－2012.

[4]国家统计局.中国统计年鉴(2002－2012)[M].北京:中国统计出版社，2002－2012.

[5]国家统计局，国家科技部.中国科技统计年鉴(2002－2012)[M].北京:中国统计出版社，2002－2012.

[6]王兴旺，汤琰洁.基于专利地图的技术预测体系构建及其实证研究[J].情报理论与实践，2013(3):51－55.

[7]曹丽江孙帅基于专利地图的我国太阳能光伏建筑一体化专利信息分析[J].情报杂志，2013(5):84－86.

[8]梁莹，徐福缘.基于多Agent的专利资源协同获取模型研究[J].情报理论与实践，2009(8):118－120.

[9]王伟.专利发展趋势预测模型的选择[J].科技情报开发与经济，2003(2):147－148.

[10]关旭，刘豹.基于Multi-Agent系统的预测支持系统的结构[J].系统工程与电子技术，2001(8):4－11.

[11]许良，毕开顺.多元线性回归分析法在蒙药森登－4汤谱效关系解析中的应用[J].计算机与应用化学，2008(10):1 189－1192.

[12]胡泽文，武夷山.科技产出影响因素分析与预测研究——基于多元回归和BP神经网络的途径[J].科学学研究，2012(7):992－1 004.