汽车盘式制动器稳定性及非线性动力学分析

刘富豪， 蒋汉军， 朱龙英

(1.盐城工学院汽车工程学院， 江苏 盐城 224051； 2.江苏安捷汽车配件有限公司， 江苏 盐城 224002；3.重庆大学机械传动国家重点实验室, 重庆 400044)

引 言

在汽车行业中，由于客户对舒适性的需求，使得降低制动器振动和噪声成为重要的研究课题。到目前为止，还没有统一的理论能解释制动器振动和噪声产生的机理和动力学特性。制动器产生振动和噪声主要是由于制动盘和摩擦片之间相互摩擦导致的。影响制动器制动噪声的因素非常复杂，除了摩擦副材料参数及其匹配性外，其刚度及质量等结构参数也是非常重要的因素，特别是高频噪声，大多在摩擦过程中发生，其机理在很大程度上取决于摩擦副的接触稳定性。根据Ibrahim，Oden，Sinou和Hoffmann等的研究成果[1～5]，主要有4种机理阐示摩擦导致的不稳定性现象：斜滑、粘滑、变动态摩擦和耦合机理。耦合机理是内共振和拍击导致的系统不稳定现象。然而，制动器噪声发生在1～16 kHz的高频[6]，很难被辨识。刘献栋等搭建了汽车盘式制动器试验台架，对制动噪声进行了试验研究，从而揭示汽车盘式制动器制动噪声产生的机理[7]。虽然制动器振动和噪声问题从20世纪30年代就开始进行研究，并获得了一些重要成果。但由于问题的复杂性，制动器振动和噪声目前仍处于研究阶段，还没有得到圆满解决。这些不足的一个重要原因是还没有统一的模型通过使用具有物理意义的参数值来解释振动和噪声问题产生的机理。另一个原因是大部分关于制动器振动的研究工作采用的是恒定的摩擦系数模型以及有限元模型，没有探索更复杂的动力学现象[5，8～12]。

对于制动系统来说，其振动和噪声与系统的稳定性有着密切的关系[2]。在现研究阶段，对制动器系统的稳定性研究成为一个热点问题。本文通过参数识别，获得了具有物理意义的制动器参数值。使用变摩擦系数，并考虑到制动力和接触刚度，克服了先前研究的不足。对提出的考虑时变摩擦系数的制动盘和摩擦片耦合的两自由度简约模型，采用劳斯赫尔维茨标准，辨识了制动器系统的稳定和不稳定域，分析了制动器主要参数对系统稳定性和共振频率的影响，阐述了模型中不同角度与极限环稳定性和幅值的关系。通过两个参数的分岔图、三个动态参数的霍普夫分岔和庞加莱截面，分析了该制动器系统的非线性动力学特性。

1 物理模型及方程

本文以盘式制动器为研究对象，其制动原理示意图如图1所示：在活塞的推动下，摩擦片在左右支架及衬块作用下和制动盘相接触，在制动盘上面产生一个阻力矩，促使制动盘停止转动。该制动器可简化成如图2所示的简约模型，制动盘和摩擦片通过滑动摩擦界面连结在一起，传输带代表制动盘，质量块m代表摩擦片的质量。在这个模型中，衬块和摩擦片之间的连接可以等价于在两个角度α1，2方向上的刚度为k1，2的两个线性弹簧。摩擦片和制动盘之间的连接可以等价于一个在垂直于制动盘方向上刚度为k3的线性弹簧，Vb为制动盘的转速。摩擦片在固定坐标系(X,Y)中任意时刻T的坐标为(X(T)，Y(T))。在制动过程中，为了防止质量块和传输带脱离接触，在质量块上加了一个初始的预紧力F。因此，整个模型受到了三个弹簧力、一个预载荷和摩擦力的作用。考虑到在稳定，滑动状态下的小扰动，该模型的动力学方程可表达为

(1)

(2)

式中k11=k1cos2α1+k2cos2α2，k12=k21=k1sinα1cosα1+k2sinα2cosα2，k22=k1sin2α1+k2sin2α2+k3。其中，k11，k12，k21和k22为耦合刚度系数。

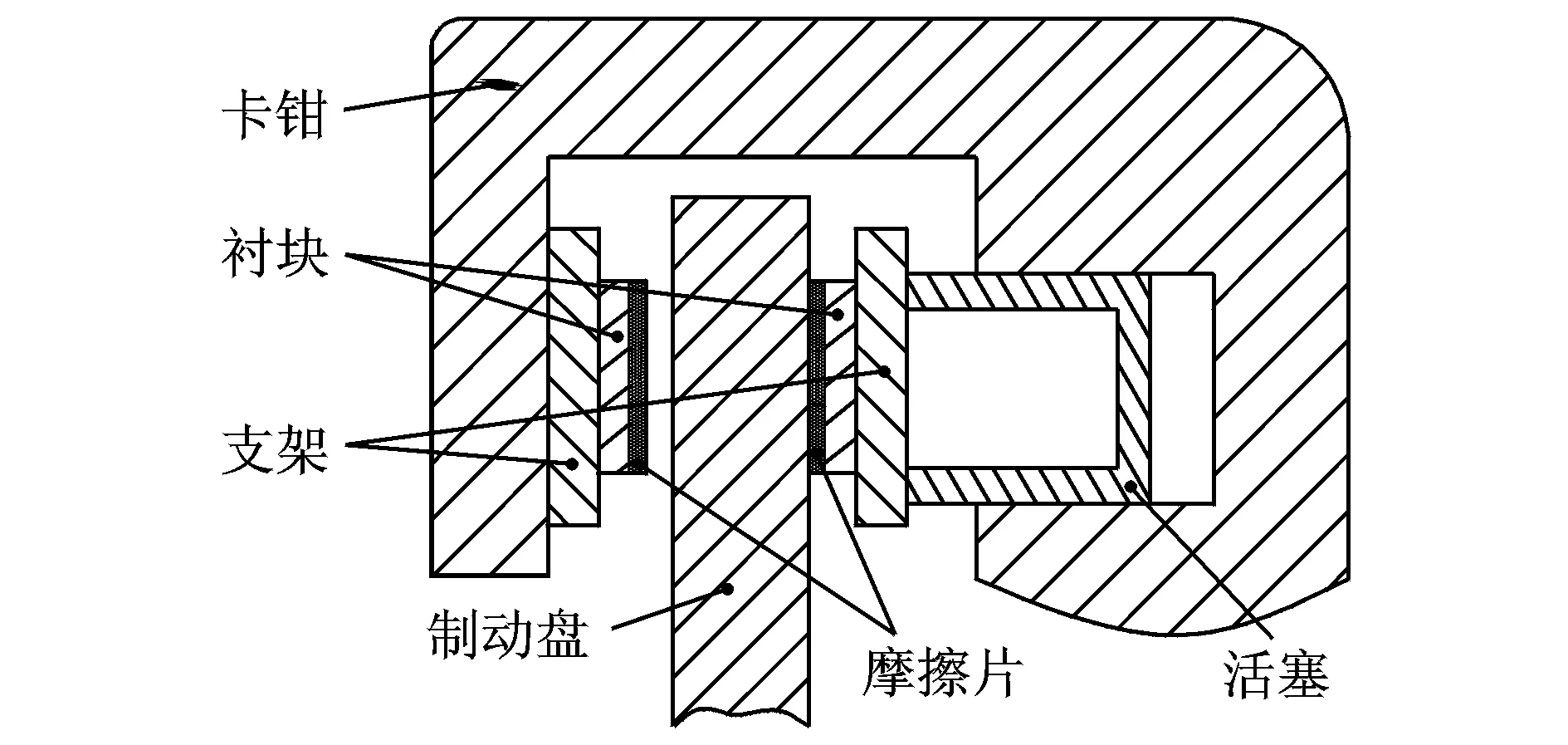
图1 盘式制动器原理示意图

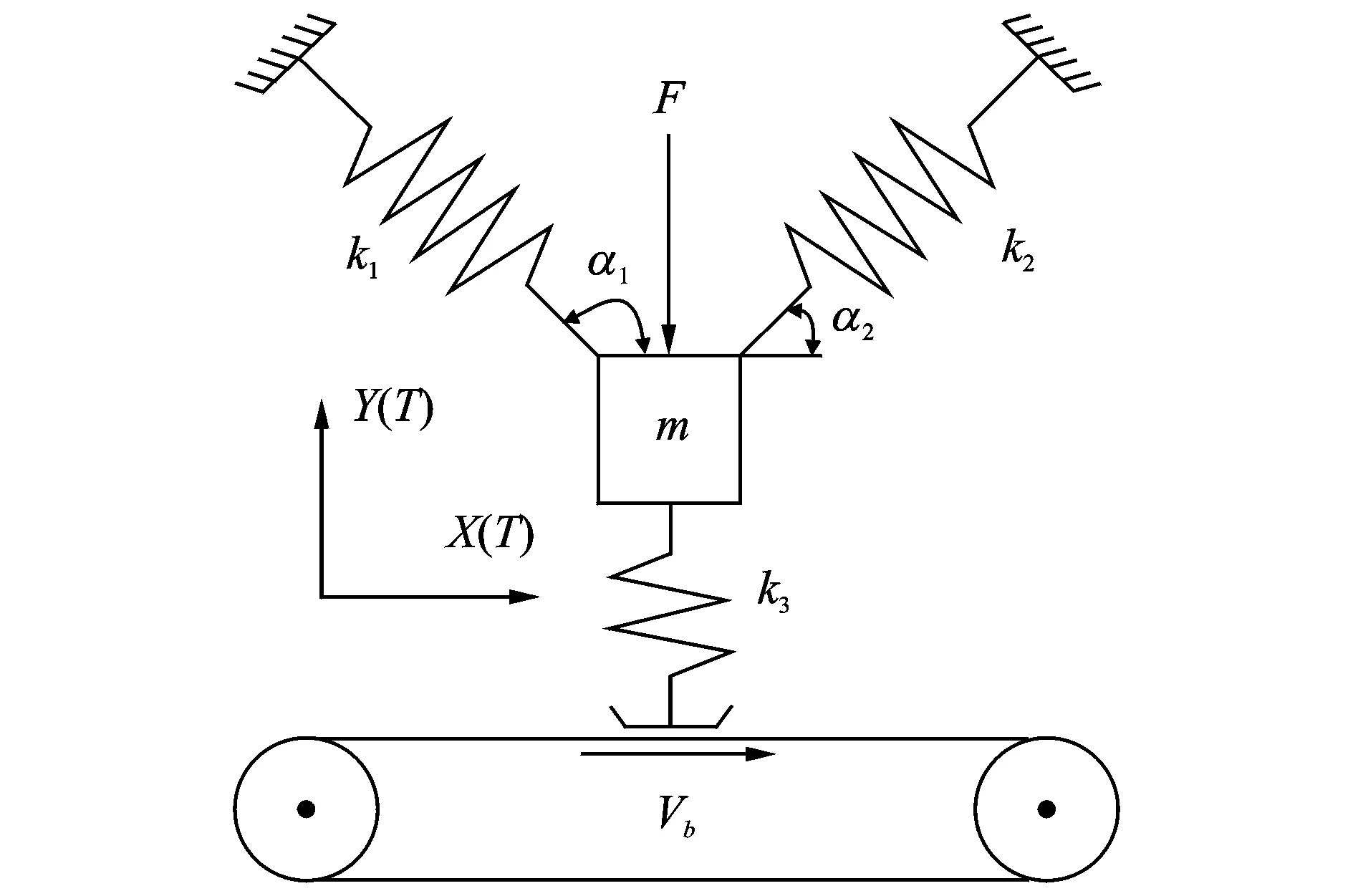
图2 制动器简约模型

对振动微分方程(1)和(2)进行归一化处理得

(3)

(4)

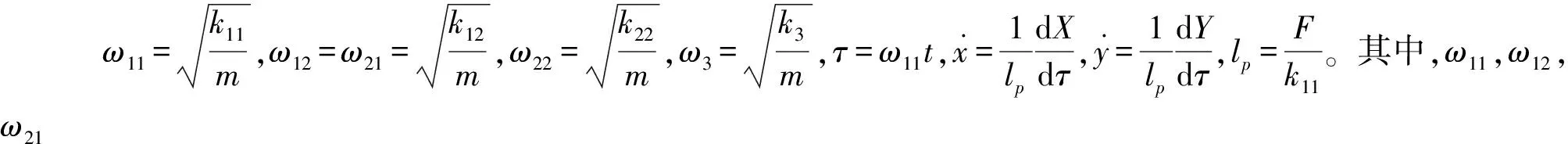
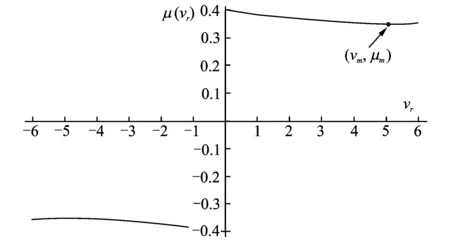
图3 Stribeck摩擦模型

非线性摩擦力是速度的函数，产生于制动盘和摩擦片之间，并激励摩擦片振动。摩擦系数随着相对滑动速度增加而相应变化，因而出现振动和噪声的可能性也会增加。当克服静摩擦力后，在低速下随着速度的增加而摩擦力减小，呈现为速度的连续函数。为了研究制动器动态特性，本文采用如下的Stribeck摩擦模型[13，14]

(5)

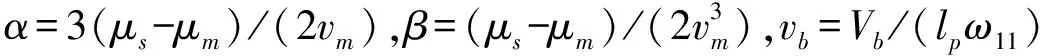
(6)

把摩擦模型方程(6)代入归一化方程(3)和(4)，可得两自由度的系统模型为：

(7)

(8)

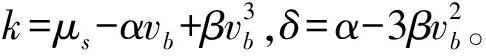
根据方程(7)和(8)，可知该系统存在一个平衡点于(x，y)=(x*，y*)，即

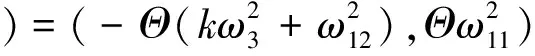
(9)

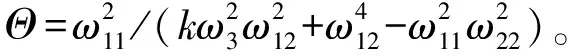
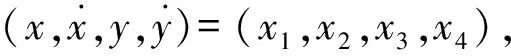
(10)

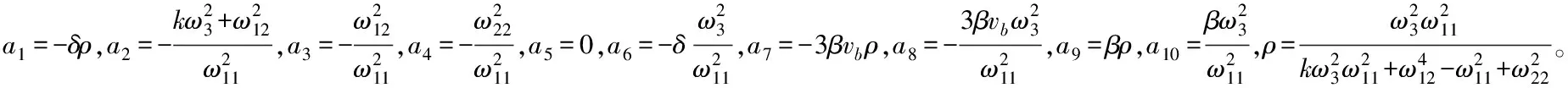
方程(10)可用于数值求解系统在变化参数情况下的稳定域及吸引子等。

2 系统稳定性和共振频率分析

对于非线性系统来说，系统的稳定性是由其线性系统决定的。稳定性主要通过计算在平衡点的雅可比行列式来研究。根据劳斯赫尔维茨标准[15]，如果系统在平衡点的雅可比行列式的特征值的实部为正值，则系统是不稳定的，同时意味着系统将会产生振动和噪声。反之，特征值的实部为负值时，系统是稳定的。特征值的虚部代表系统的频率。

在固定点，方程(10)的雅可比行列式为

(11)

雅可比行列式(11)的特征方程为

λ4+p3λ3+p2λ2+p1λ=0

(12)

式中ρ0=-a2a3-a4，p1=a1a4，p1=1-a4，p3=-a1。

特征值实部的符号可通过多项式(12)的系数确定，根据劳斯赫尔维茨标准，为确保系统稳定，必须使特征值实部为负，因此需定义如下条件：

(a)p3>0

(b)p2p3-p1>0

(c)p1(p2p3-p1)-p0p2>0

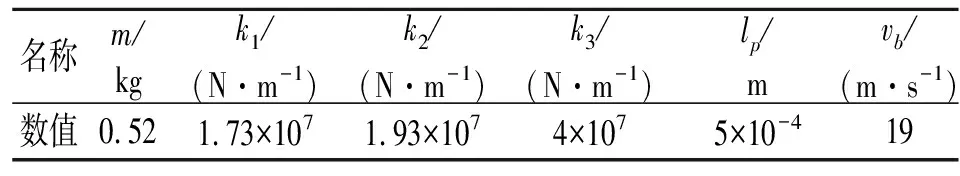
表1 基于试验的物理参数

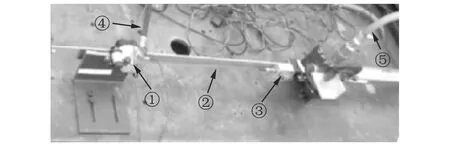
图4 简易制动系统试验台：①带有刹车片的简易制动器;②导杆;③传感器;④导气管1;⑤导气管2

表1中的参数是在简易制动系统试验台上测量的。如图4所示，导杆通过气缸产生的拉力在带有刹车片的简易制动器中运动，其速度可以通过传感器测量出来，简易制动器通过气缸产生的压力对导杆进行制动，气缸产生的拉力和制动所需的压力均可通过导气管中的气流大小来控制。通过模态识别法获得简易制动器系统在各个方向上的刚度值。使用表1中的基本参数，随着角度α1的变化，相应的特征值的实部及频率如图5～7所示。在使用库仑摩擦模型的情况下，当α1∈(1.57±1.57，4.06±1.57)rad，特征根是一对纯虚数。在这种情况下，系统是临界稳定的，其动力性行为取决于非线性条件。霍普夫分岔产生的极限环将会出现于该系统，系统在平衡点附件的稳定性问题转换为系统周期解稳定性的问题。当α1∈(4.06±1.57，4.71±1.57)rad，两个模态耦合，形成复杂的一对，系统将会出现内共振。这就表明即使摩擦系数为常数，对于盘式制动器来说，振动和噪声仍然可以发生[16]。在图5和6中，由于负斜率摩擦的存在，当α1∈(1.57±1.57，2.25±1.57)∪(3.22±1.57，4.06±1.57)rad，系统也是不稳定的，这与负斜率摩擦-速度曲线导致的负阻尼不稳定相一致[17]。另外，由于有两个模态非常接近，拍击振动将会发生在系统中。在这里，共振频率使系统不稳定，非共振频率使系统出现拍振。这一结果证实，分离共振频率及拍振是在设计阶段降低制动器出现振动和噪声现象的重要途径。同时，系统在不同角度下所表现出来的稳定性特征表明了制动器的结构因素在制动振动的产生过程中起到了关键的作用[18]。

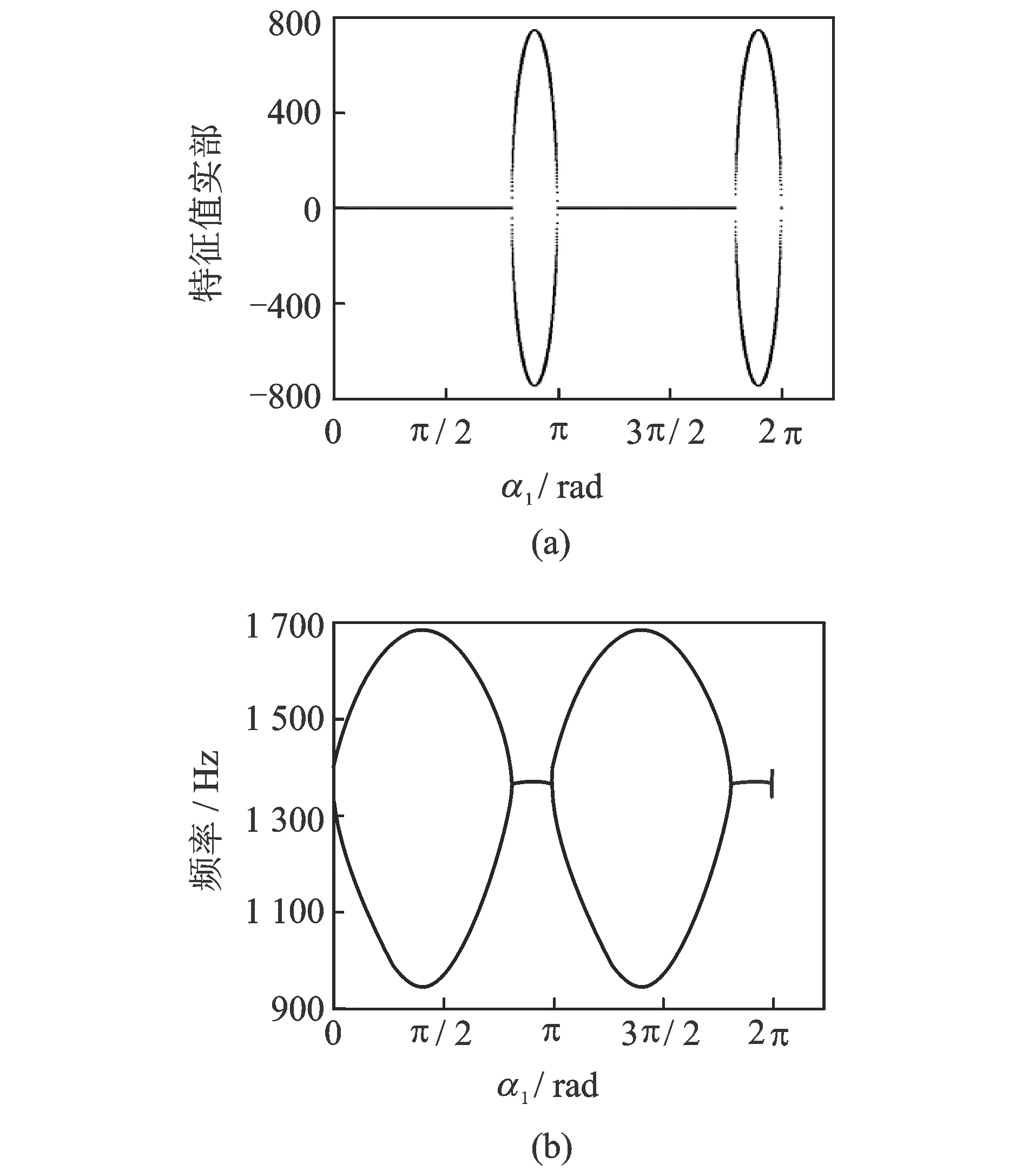
图5 库仑摩擦模型特征值实部和频率随角度α1的变化

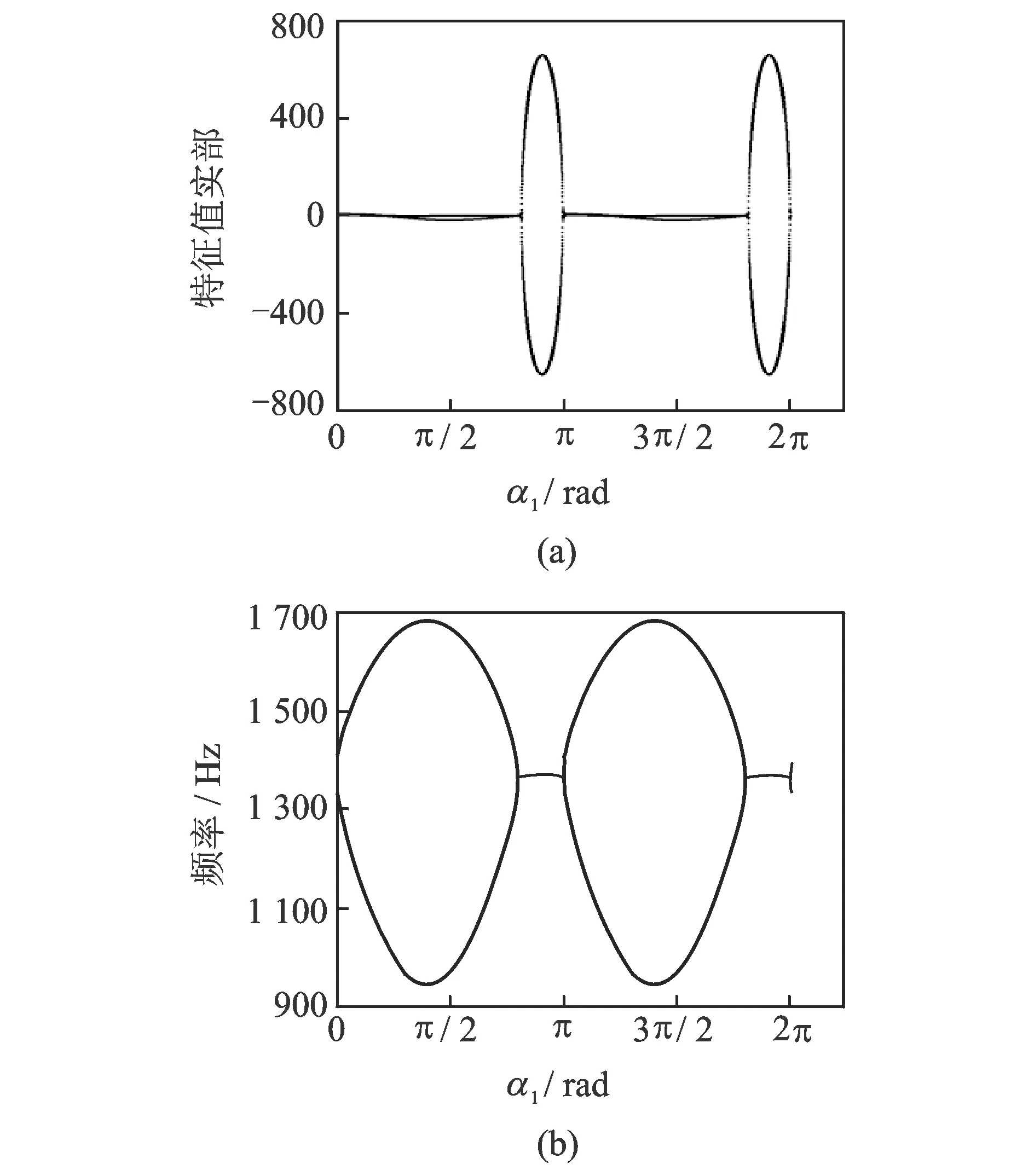
图6 Stribeck摩擦模型特征值实部和频率随角α1的变化

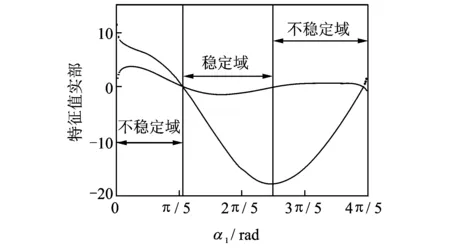
图7 Stribeck摩擦模型特征值的实部局部放大图

稳定性是一个复杂的问题，图8(a)～图11(a)显示了随不同参数组合时系统的稳定和不稳定域。其中，实心点代表稳定域，空心点表示不稳定域。为了分析共振频率，特征值在复平面上的实部和虚部如图8(b)～图11(b)所示。横坐标为系统阻尼或等效阻尼，复平面右边模态是负阻尼，为不稳定域。相反，左边模态是解耦的，代表稳定域。从图5～7和图8(b)～11(b)可知，耦合模态出现于正负模态同时存在的情况下。

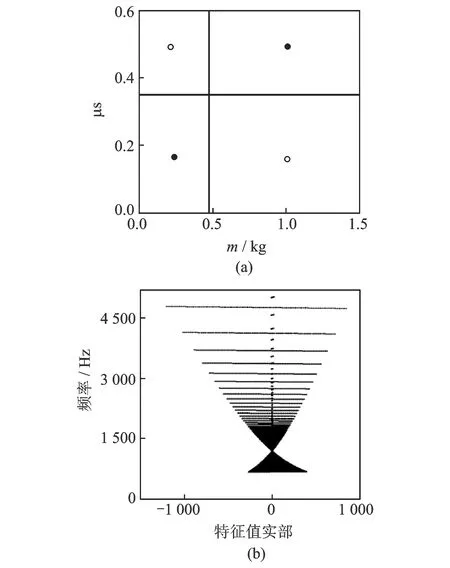
图8 稳定域和耦合共振频率随质量m和静摩擦系数μs的变化

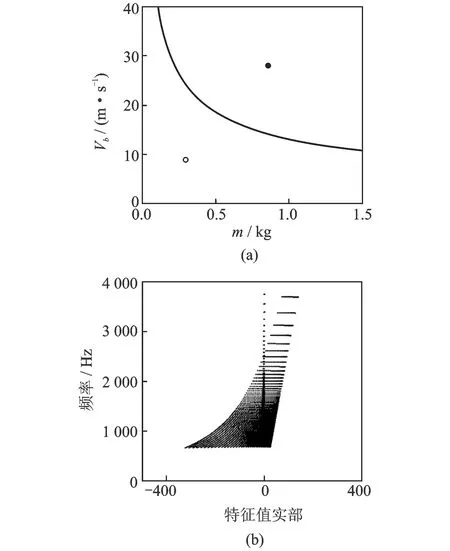
图9 稳定域和耦合共振频率随质量m和转速Vb的变化

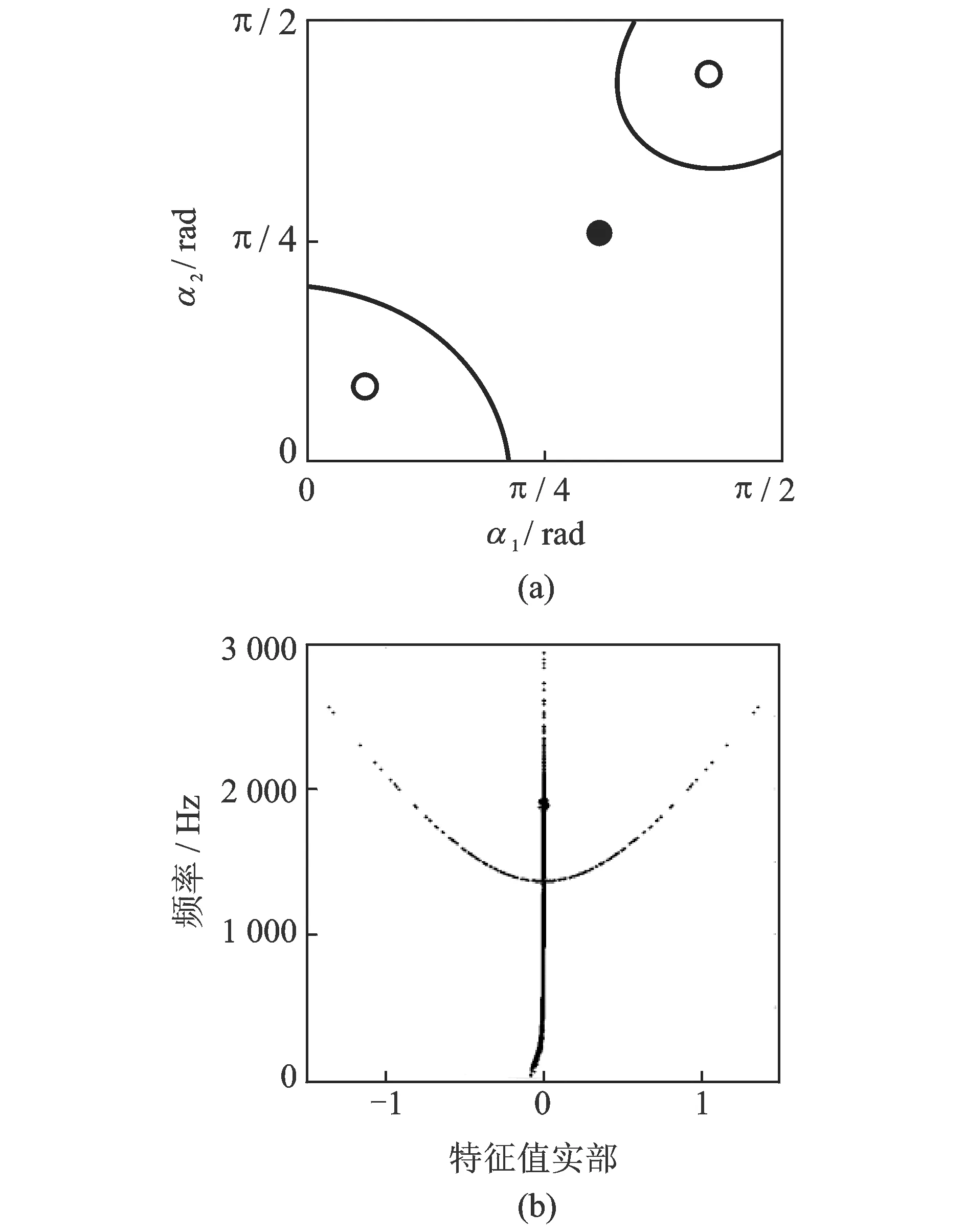
图10 稳定域和耦合共振频率随角度α1和α2的变化

从图8(a)和9(a)可知，在小质量摩擦片、大转速和大的摩擦系数或大质量摩擦片、小转速和小的摩擦系数情况下，制动器更容易产生振动和啸叫。从图10(a)和11(a)可知，当摩擦片的两个支撑角度同时取值较小或较大时，或者摩擦片刚度k1较大时，系统更容易趋向不稳定。从图8(b)和11(b)可得出，各参数组合情况下，出现耦合共振频率的范围。

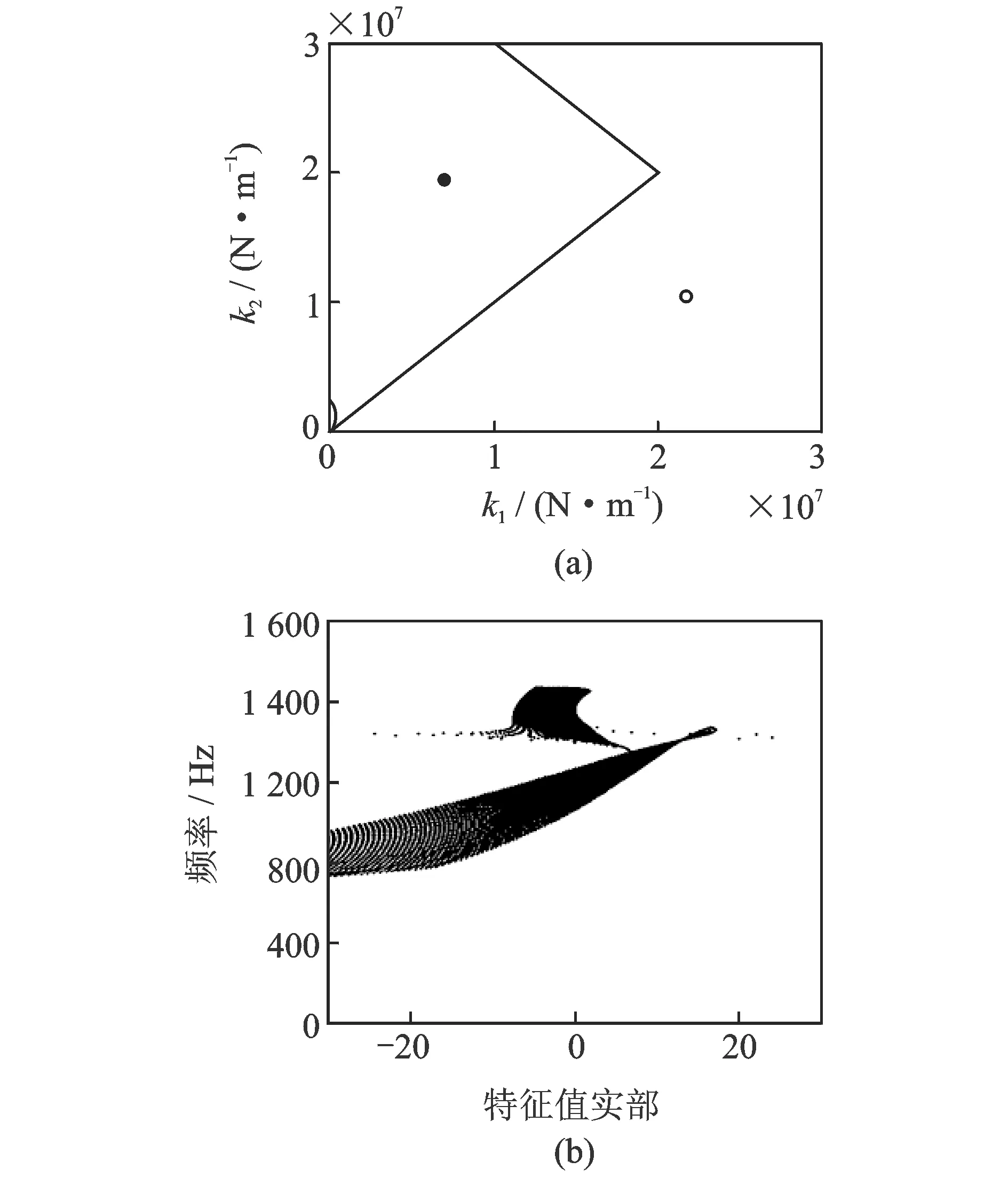
图11 稳定域和耦合共振频率随刚度k1和k2的变化

值得注意的是，系统稳定性极大地依赖于所选择的参数值，设计者可通过调整摩擦片质量和刚度、制动盘转速和材料的摩擦系数等参数，使系统达到稳定状态，降低制动器振动。

3 非线性分析

非线性分析可以提供极限环大小和混沌信息，以及对系统稳定性的影响和共振现象的关系。稳定的极限环是非常重要的，即使在没有周期外力的情况下，也会使模型系统表现出自激振动。然而，由于系统中存在拍振，很难在不同角度的情况下比较极限环的大小。为了更好地理解角度对极限环振幅的影响，极限环的半径将由位移的均方值(RMS)代替，由方程(10)进行数值积分得到。

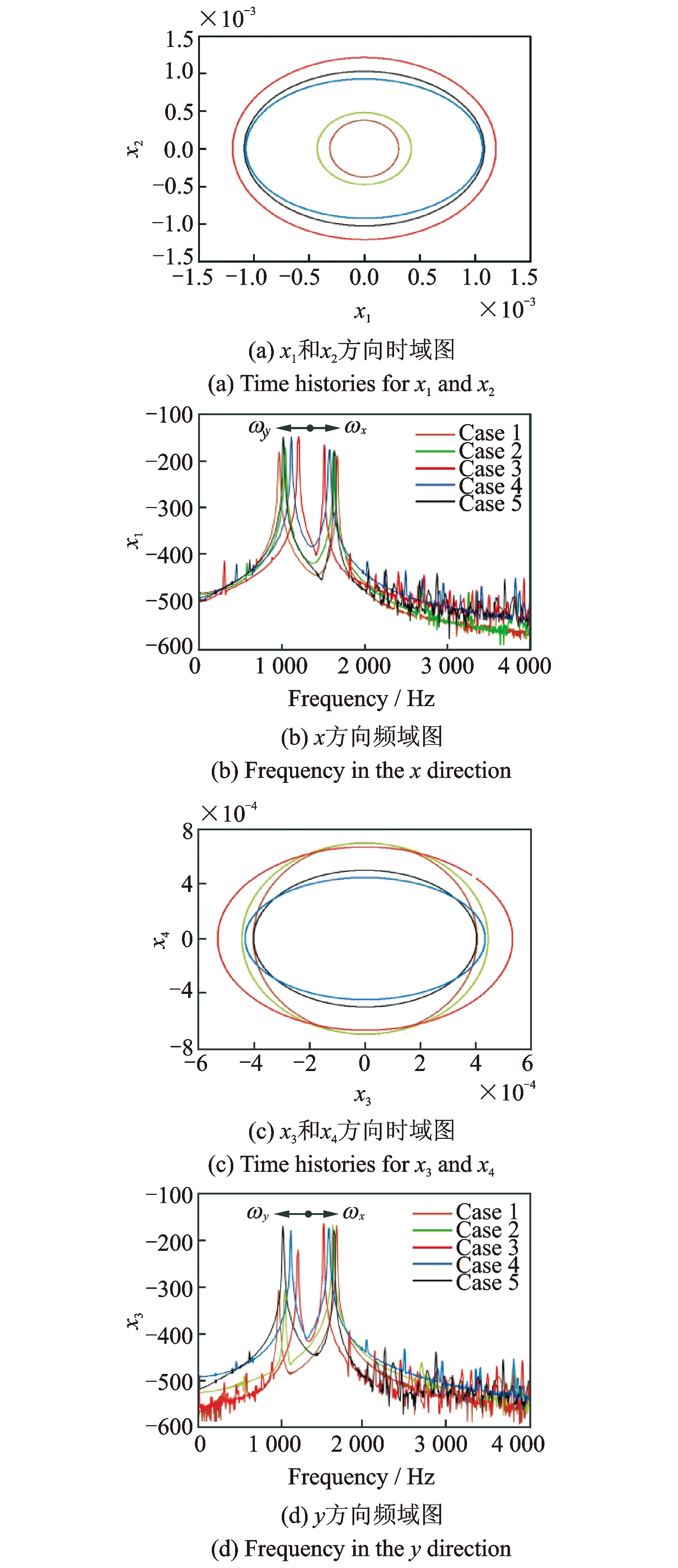
图12 当(α1，α2)=(π，0)rad时x和y方向上的振动

图12示出了极限环在不同角度下的演变。首先，根据表2中的实例，当(α1，α2)=(3.14，0.63)rad时，第一李雅普诺夫系数是负的，所以有一个超临界Hopf分岔。并且负的Lyapunov指数意味着从失稳后变成稳定的周期分叉，所以这个极限环是稳定的。随着角度α1和α2的减少，Hopf分岔变成次临界的，极限环出现了不稳定。其次，由图12可看出，极限环在两个方向上的大小是不一样的。随着角度α1和α2的增大，极限环的半径在x方向上是增加的，直到到达实例3的情况，然后又减少。最后，随着角度α1和α2的增大，拍振频率也相应增大。由图12和表2可知，在这个非线性系统中，弹簧的角度影响了极限环的振幅和稳定性。

表2 极限环的三个动态参数：第一李雅普诺夫系数(α)，第一李雅普诺夫指数(L1)，李雅普诺夫维数(dL)

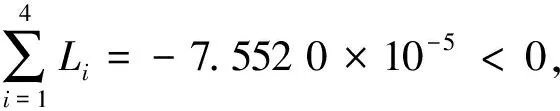
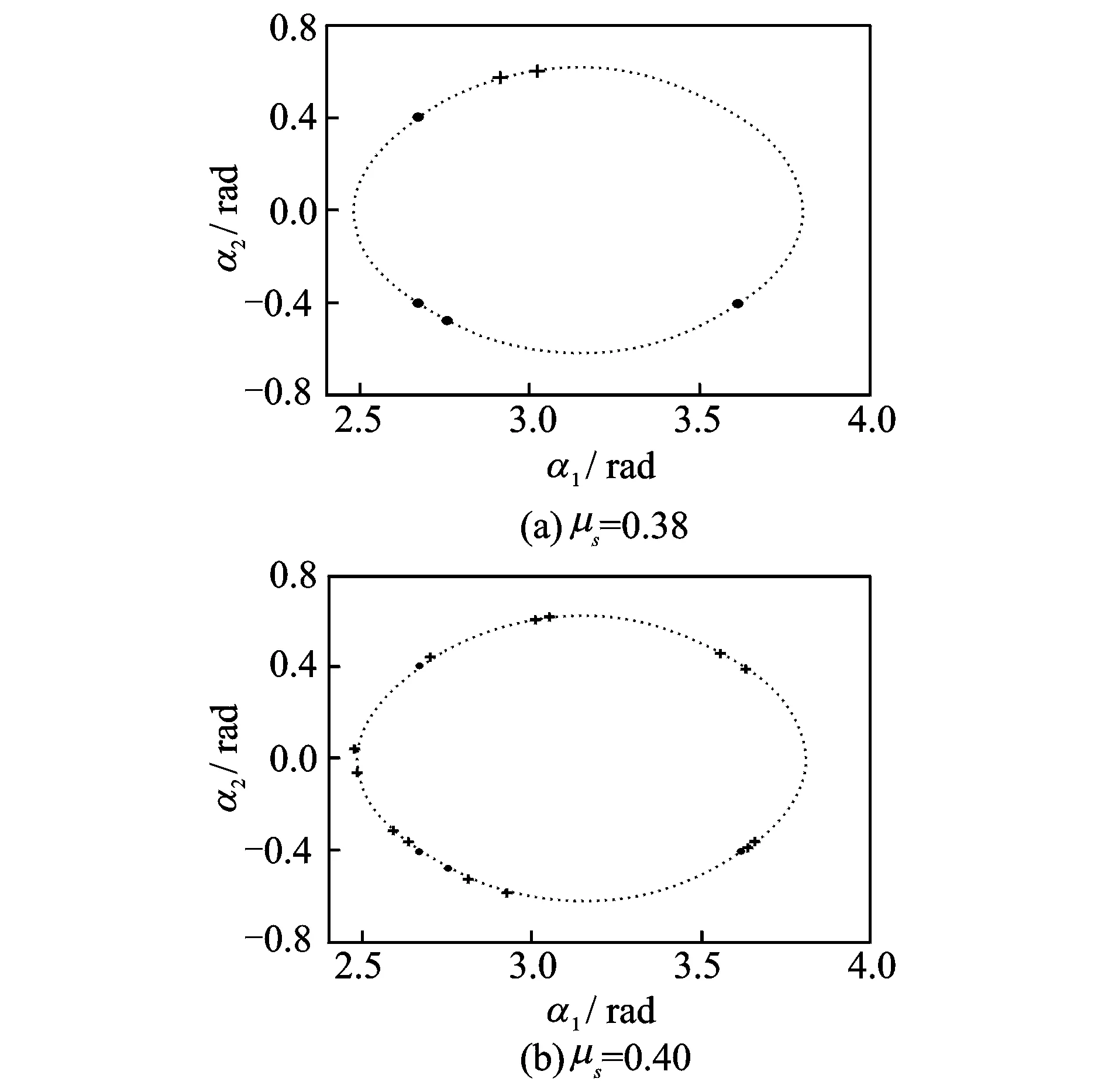
图13 关于角度的两个参数分岔曲线图(+:双Hopf分叉点;·: 广义Hopf分岔点)

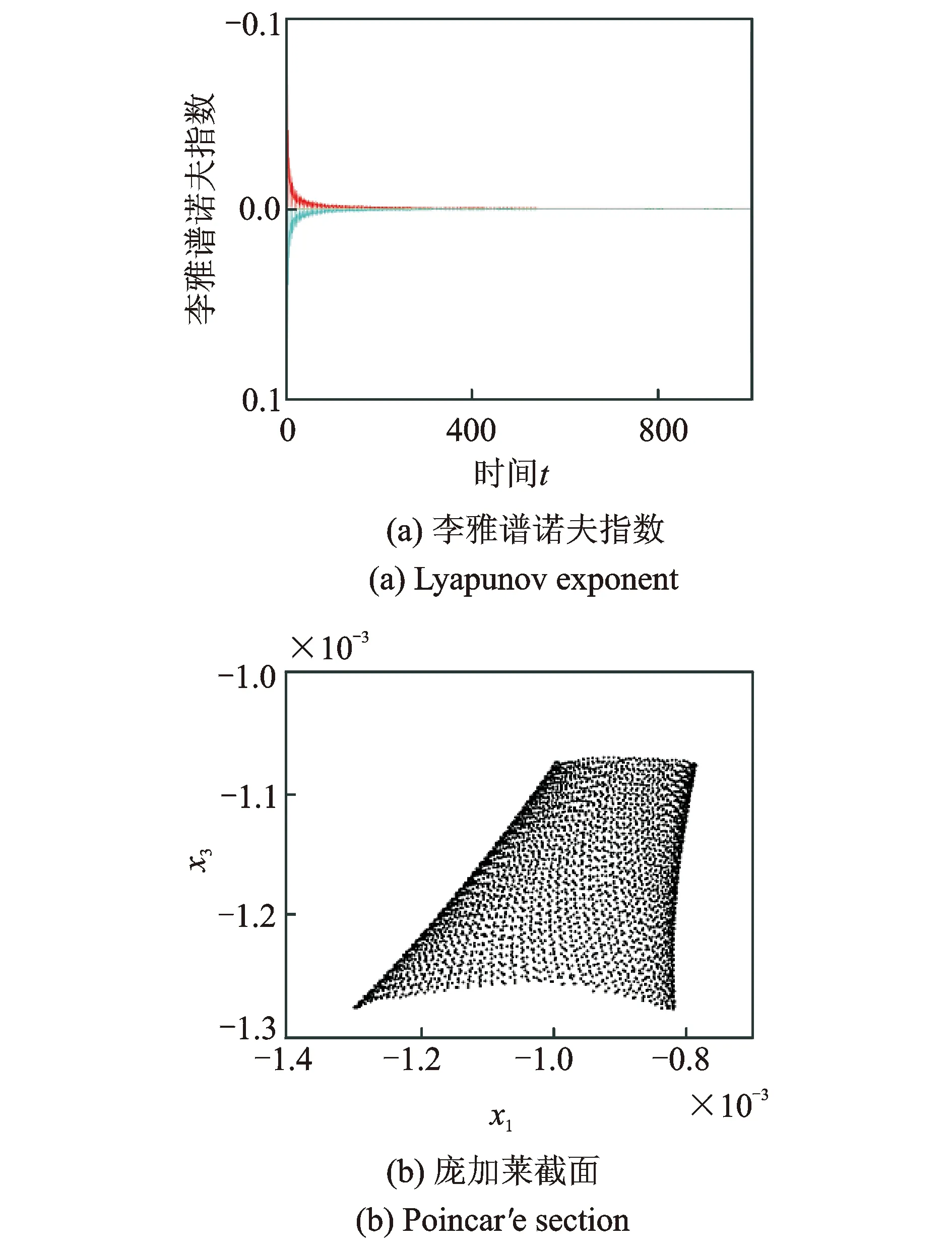
图14 李雅普诺夫指数(实例3)和庞加莱截面图(x2=0)

图15示出了x1方向振动位移的吸引子随接触刚度k3的变化，当接触刚度k3的值接近2×107N/m附近时，相对于其他条件下，在x1方向上运动的幅度变得越来越大，这意味着该系统的振荡很显著。这为制动系统的优化提供了一个基本参考。

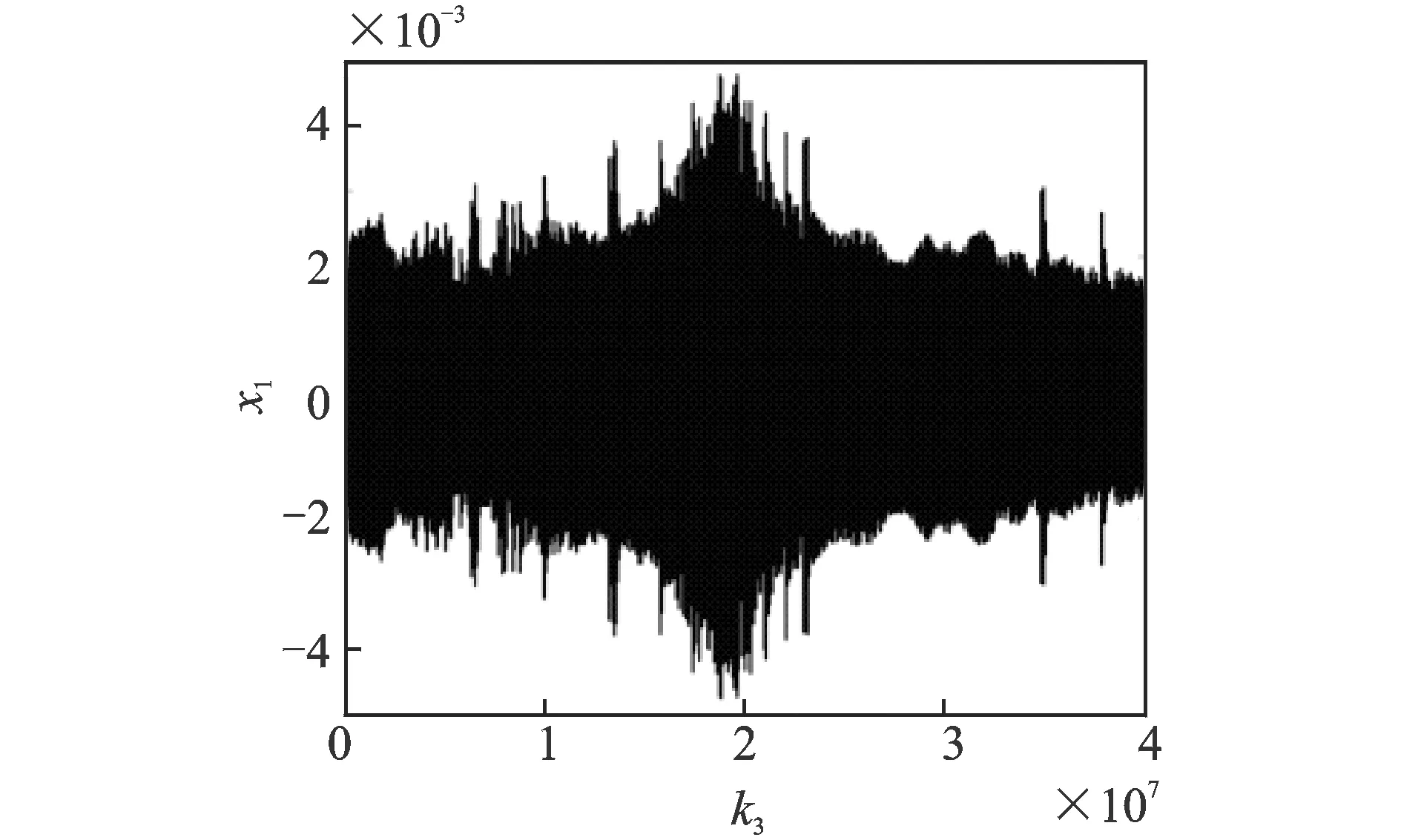
图15 接触刚度k3的吸引子

4 结 论

制动器振动和噪声机理复杂，在不同的工况下可能存在不同的产生机理。基于变摩擦系数，本文采用了针对制动器振动的简约模型，分析了不同参数对系统稳定性和共振频率的影响。可得出以下结论：

(1)对比库仑摩擦模型，负斜率摩擦模型更容易导致系统出现不稳定；

(2)分离共振频率和拍振是在设计阶段降低制动器出现振动现象的重要途径。

(3)摩擦片的质量、刚度及制动盘的转速对制动器系统稳定性影响很大。在小质量摩擦片、大转速和大的摩擦系数或大质量摩擦片、小转速和小的摩擦系数情况下，以及摩擦片的两个支撑角度同时取值较小或较大时，或者摩擦片刚度k1较大时，系统更容易趋向不稳定，使制动器产生振动。

(4)角度不仅影响了系统在平衡点处的稳定性，还会影响到周期解的稳定性和极限环的幅值。随着角度增大，极限环从不稳定变成稳定。

(5)制动盘和摩擦片等零件的质量和结构刚度经过优化设计，合理匹配，可以降低制动振动。

参考文献:

[1] Ibrahim R. Friction-induced vibration, chatter, squeal, and chaos-Part I: Mechanics of contact and friction[J].Applied Mechanics Reviews, 1994,47(7):209—226.

[2] Ibrahim R. Friction-induced vibration, chatter, squeal, and chaos-Part II: Dynamics and modeling[J].Applied Mechanics Reviews, 1994,47(7):227—253.

[3] Sinou J, Thouverez F, Jezequel L. Analysis of friction and instabilityby the centre manifold theory for a non-linearsprag-slip model[J]. Journal of Sound and Vibration, 2003,265(3):527—559.

[4] Oden J, Martins J. Models and computational methods for dynamic friction phenomena[J]. Computer Methods in Applied Mechanics and Engineering, 1985,52(1-3):527—634.

[5] Hoffmann N, Fischer M, Allgaier R, et al. A minimal model for studying properties of the mode-coupling type instability in friction induced oscillations[J]. Mechanics Research Communications, 2002,29(4):197—205.

[6] 黄学文，张金换，董光能，等.汽车摩擦制动噪声研究进展与发展趋势[J].汽车工程，2007,29(5)：385—388.Huang Xuewen, Zhang Jinhuan, Dong Guangneng, et al. Progress and development trend of research on friction-induced brake squeal of vehicles[J]. Automotive Engineering，2007,29(5)：385—388.

[7] 刘献栋，任增杰，王海霞，等.盘式制动器摩擦特性及制动尖叫测试与分析[J].振动测试与诊断，2013，5：746—750.Liu Xiandong, Ren Zengjie, Wang Haixia, et al. Test and analysis of friction characteristics and brake squeal of automotive disc brake[J]. Journal of Vibration, Measurement & Diagnosis,2013，33(5)：746—750.

[8] Sinou J, Thouverez F, Jezequel L. Analysis of friction and instabilityby the centre manifold theory for a non-linearsprag-slip model[J]. Journal of Sound and Vibration, 2003,265(3):527—559.

[9] 陈光雄，戴焕云，曾京，等.踏面制动尖叫噪声的有限元分析[J].机械工程学报，2009,45(3):203—207.Chen Guangxiong, Dai Huanyun, Zeng Jing, et al. Finite element analysis of the squeal propensity for a pad-wheel tread brake system[J]. Journal of Mechanical Engineering, 2009,45(3):203—207.

[10] 余为高，于学华.应用有限元法对盘式制动器制动噪声分析[J]. 科学技术与工程，2009,9(12):3 234—3 236.Yu Weigao, Yu Xuehua, Analysis of disc brake noise based on finite element methods[J]. Science Technology and Engineering, 2009,9(12):3 234—3 236.

[11] Fritz G, Sinou J, Duffal J, et al. Investigation of the relationship between damping and mode-coupling patterns in case of brake squeal[J]. Journal of Sound and Vibration, 2007,307(3-5):591—609.

[12] 戴轶,张嵩.盘式制动片的特征参数对制动噪声的影响[J].振动与冲击，2006，25(6):162—166.Dai yi, Zhang Song. Effect of disc brake pad parameters on squeal noise[J]. Journal of Vibration and Shock, 2006,25(6):162—166.

[14] 黄毅，丁千.内共振系统的干摩擦自激振动[J].振动与冲击, 2008,27(5):103—104.Huang Yi, Ding Qian. The self-excited vibration of a dry-friction system with internal resonances[J]. Journal of Vibration and Shock, 2008,27(5):103—104.

[15] Cesari L. Asymptotic Behavior and Stability Problems in Ordinary Differential Equations[M]. Academic Press, 1963.

[16] Millner N. An analysis of disc brake squeal[J]. SAE International ,Technical Paper 780332, 1978.

[17] Sheng Gang. Friction-induced Vibrations and Sound: Principles and Applications[M]. CRC Press, 2008.

[18] 李清，刘佐民, 蔡萼华,等.浮钳盘式制动器结构稳定性仿真分析[J].武汉理工大学学报(信息与管理工程版),2008,30(5):744—748.Li Qing, Liu Zuomin, Cai Ehua, et al. Simulation analysis of the construction stabilization of the floating disk brake[J]. Journal of WUT (Information & Management Engineering)，2008,30(5):744—748.

[19] Grebogi C, Ott E, Yorke J A. Fractal basin boundaries, long-lived chaotic transients, and unstable-unstable pair bifurcation[J]. Physical Review Letters, 1983,50(13):935—938.