引入不确定参数的汽车盘式制动器振动稳定性分析

吕 辉， 于德介， 陈 宁， 夏百战

(湖南大学汽车车身先进设计制造国家重点实验室， 湖南 长沙 410082)

引 言

盘式制动器以其优异的性能在汽车上得到了广泛的应用，但制动器结构如果设计不合理，就有可能在工作过程中处于不稳定状态，引起强烈的振动，并形成刺耳的噪声。

在汽车制动噪声的频率范围中，以1～16 kHz之间的尖叫声最困扰乘客的听觉，严重影响汽车的舒适性[1]。针对汽车制动噪声问题，不少学者通过对制动器系统的复特征值进行分析来判断系统的稳定性，从而预测制动噪声的产生趋势。基于有限元的复特征值分析方法是一种研究制动器系统稳定性的有效方法[2]。文献[3]从子结构模态的角度对制动器稳定性进行研究，基于制动器摩擦闭环耦合有限元模型求解了系统复特征值的正实部，分析了正实部对子结构模态参数的灵敏度，将敏感参数作为优化参数进行研究，提出了修改制动盘和支撑支架的改进措施。该研究在汽车盘式制动器制动噪声的预估和抑制上取得了很好的效果，但没有考虑参数的不确定性及系统稳定性的可靠性问题；且对参数进行灵敏度分析时，采用的是基于偏导理论的局部灵敏度分析。

在工程实际中，材料特性和作用载荷等参数往往具有不确定性，考虑各设计参数的不确定性构建随机模型进行分析，能更好地反映工程实际[4]。可靠性分析能保证随机模型不因参数的波动而失效，但复杂工程结构可靠性问题的功能函数通常具有高维数、隐式表达和非线性等特征，导致可靠性分析过程的计算量过大，从而影响了各种可靠性分析方法在工程实际中的推广应用。蒙特卡洛法作为求解结构可靠性的重要方法之一，对仿真问题的维数不敏感，且不受任何假设的约束，可通过大量的随机抽样获取较高的求解精度，具有很强的适用性[5]。

由于工作环境多变和结构复杂，因此制动器振动噪声是很多不确定参数共同影响的结果，难以捕捉和重复，适合采用随机模拟和统计试验方法进行研究。局部灵敏度分析只能分析确定性参数发生微小变化时对系统性能的影响，应用于制动器系统上有一定的局限性。全局灵敏度法[6]考虑了参数的概率分布情况对输出的影响，并且分析时所有参数可以大范围同时变化，适用于具不确定参数的制动器系统分析。Sobol′法[7]是一种基于方差的全局灵敏度分析法，与其他全局灵敏度分析法相比，它能够采用蒙特卡洛法快速简便计算出各阶灵敏度和高阶交叉影响项。

本文将基于蒙特卡洛法的可靠性分析引入到汽车盘式制动器稳定性研究中，采用随机和区间参数对制动器系统进行描述，将响应面法与有限元复特征值技术相结合，实现了制动器振动稳定性的可靠性分析模型的参数化，大大提高了分析效率。采用蒙特卡洛法分析了系统参数为正态分布随机参数和区间参数下，某型车的浮钳盘式制动器系统的稳定性可靠度，结合Sobol′法对系统参数进行了全局灵敏度分析，甄别了不确定性参数对系统稳定性的影响，并从可靠性角度提出了改善制动器系统振动稳定性的工程措施，不确定性分析技术的引入提高了传统研究方法的适用性，分析方法对抑制制动噪声具有一定的工程指导性。

1 汽车盘式制动器振动稳定性

以汽车盘式制动器为研究对象，系统的运动方程可以表示为[8]

(1)

式中M，C和K分别为无摩擦制动器系统的质量矩阵、阻尼矩阵和刚度矩阵，Kf为摩擦接触刚度矩阵，u为系统在平衡位置附近振动的广义位移向量。

由式(1)可知，引入摩擦力后，系统的刚度矩阵不对称，系统的特征值在一定条件下为复数，即系统对应的模态为复数。

式(1)的解可写成如下形式

u=φeλt

(2)

式中φ为振型矩阵，λ为系统特征值。上式代入式(1)，得

(λ2M+λC+K-Kf)φ={0}

(3)

若系统第i阶特征值为复数，则可表示为

λi=αi+jβi

(4)

式中αi为特征值实部，是系统的阻尼系数，βi为特征值虚部，是系统的自然频率。

与第i阶特征向量对应的系统响应可表示为

ui=φieαitcosβit

(5)

参考文献[9]，定义系统第i阶阻尼比

(6)

由式(5)和(6) 可知，若某阶阻尼比为负，则对应的特征值具有正实部，系统是不稳定系统，系统随着时间推移而放大振动。系统阻尼比为负时可等效为系统存在负阻尼，此时阻尼不耗散能量，反而向系统中馈入能量，形成自激振动，引发制动噪声，以噪声的形式向外辐射能量。因此根据系统的阻尼比可以判断系统的稳定性，预测系统出现制动噪声的趋势。

2 基于可靠性的汽车盘式制动器振动稳定性分析

2.1 基于蒙特卡洛的可靠度分析

可靠性分析能保证结构模型不因参数的波动而失效。若结构参数为随机变量，则结构可靠度的计算公式为

(7)

式中R表示可靠度，Pr表示概率，fX(X)为独立随机向量X的联合概率密度函数，g(X)为功能函数，可表示结构的两种状态

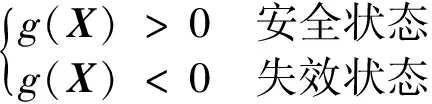
(8)

g(X)=0为极限状态方程，是一个多维数曲面，称为极限状态面或失效临界面。

蒙特卡洛法又称随机模拟法或统计试验法，是一种依据统计抽样理论，从已知概率分布的变量中随机抽样，依据随机抽样结果计算输出的数字特征。采用蒙特卡洛法进行可靠度分析，式(7)表示为

(9)

式中I[ ]为特征函数，且满足

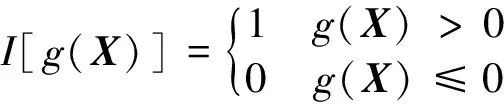
(10)

可靠度的蒙特卡洛近似估计为

(11)

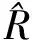
若在结构中引入区间参数，则结构的可靠度为

R=Pr{g(X,Y)≥0}

(12)

式中Y为区间向量

Y∈[YL,YU]

(13)

式中 L和U分别表示参数的下界和上界。功能函数的蒙特卡洛估计量满足

Y∈Y

(14)

特征函数满足

(15)

结合式(11)得可靠度区间为

R∈[RL,RU]

Y∈Y

(16)

2.2 Sobol′全局灵敏度分析

传统的灵敏度分析是在一个变量产生微小变化的同时保持其他变量不变，观察由变量变化引起的结果变动。在工程实际中，考虑变量在某一大的范围内变化且计及多个变量相互影响的全局灵敏度信息具有更高的参考价值。

本文采用Sobol′法进行全局灵敏度分析，Sobol′法是一种基于方差的蒙特卡洛法[10]，其主要思想是将函数f(z)分解成2n项递增项之和，通过采样计算模型响应的总方差及各项偏方差，从而求得灵敏度。在输入参数域In为n维单元体的情况下，将函数f(z)分解为2n个递增项之和

f1,2,…,n(z1,z2,…,zn)

(17)

式中f0为常量，且其他加数项对其所包含任意一变量的积分必定为零，即

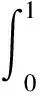
(18)

由式(17)，(18)可知，式(17)中的所有加数项之间都是正交的，且可以表示为函数f(z)的积分

(19)

(20)

(21)

由此类推，即可求出式(17)中的其他高阶项。

将式(17)两边平方并在整个参数域In内积分，结合式(18)有

(22)

函数f(z)的总方差D为

(23)

偏方差为

(24)

由式(22)可知

(25)

这样，全局灵敏度指数就可以表示为

Si1,…,is=Di1,…,is/D

(26)

Sobol′法的一个显著特点是对于式(23)和(24)的定积分，可直接用蒙特卡洛法求得。

实际工程中的参数域一般不在[0,1]的范围内，本文按式(27)对参数进行离差标准化

(27)

2.3 汽车盘式制动器稳定性分析

由第1节分析可知，特征值阻尼比ζ是表征制动器系统稳定性的指标。为在一定程度上保证系统的稳定性，ζ应大于某一临界值ζc，参考文献[11] ，取ζc=-0.01。由此本文从可靠性角度提出如下功能函数

g(Z)=g(X,Y)=ζ(Z)-ζc=ζ(Z)+0.01

(28)

式中Z为随机或者区间变量，ζ(Z)为目标特征值阻尼比。

本文提出的基于蒙特卡洛法与全局灵敏度的汽车盘式制动器稳定性分析方法主要步骤为:

(1)基于制动器系统的有限元模型，在不确定参数空间进行试验设计，求出系统对应各组试验样本的各阶特征值；

(2)选择特征值实部大于0的特征值为研究对象，建立系统目标特征值的参数化响应面模型；

(3)基于特征值响应面模型，建立系统可靠性研究的功能函数参数化模型；

(4)基于功能函数模型，采用蒙特卡洛法对系统的可靠性进行分析；

(5)采用Sobol′法对系统不确定参数进行全局灵敏度分析；

(6)根据灵敏度研究各参数对制动器系统稳定性的影响，并从可靠性的角度提出提高系统稳定性的改进方案。

本文方法的具体分析步骤如图1所示。

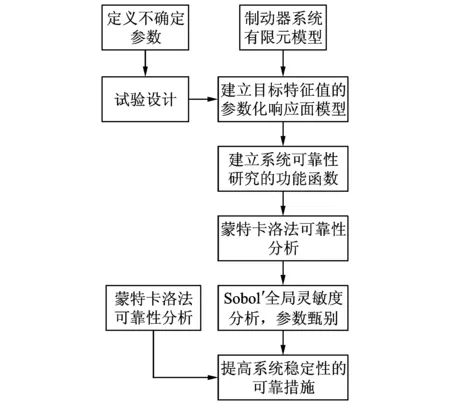
图1 基于可靠性的制动器振动稳定性分析

3 算例研究

3.1 汽车盘式制动器参数化模型

本文利用Altair. Hypermesh软件建立了某型轿车的制动器有限元简化模型，如图2所示。

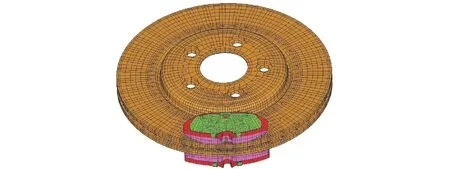
图2 制动器有限元模型

简化模型由制动盘、制动片、支撑背板和绝缘板等部分组成，共划分成26 125个实体单元，37 043个节点，制动片与制动盘之间为摩擦接触面，整个系统为一个摩擦耦合系统。有限元复特征值分析主要与材料密度、弹性模量和载荷约束等条件有关。本文选取各部件材料密度、弹性模量、摩擦系数和制动压力作为不确定量。由于摩擦损耗引起的是部件刚度的改变，因此磨损引起的不确定性可由材料弹性模量的不确定性间接体现。参考文献[12]，给出不确定变量的分布类型和取值如表1所示。

表1中的正态分布采用截断高斯分布，即使用带有上下界的正态分布，从而在抽样中忽略掉概率极小的样本，使得所有不确定参数的波动范围均为其均值的±5%。为便于试验设计和Sobol′法求解灵敏度，本文按下式将各设计变量进行离差标准化

(29)

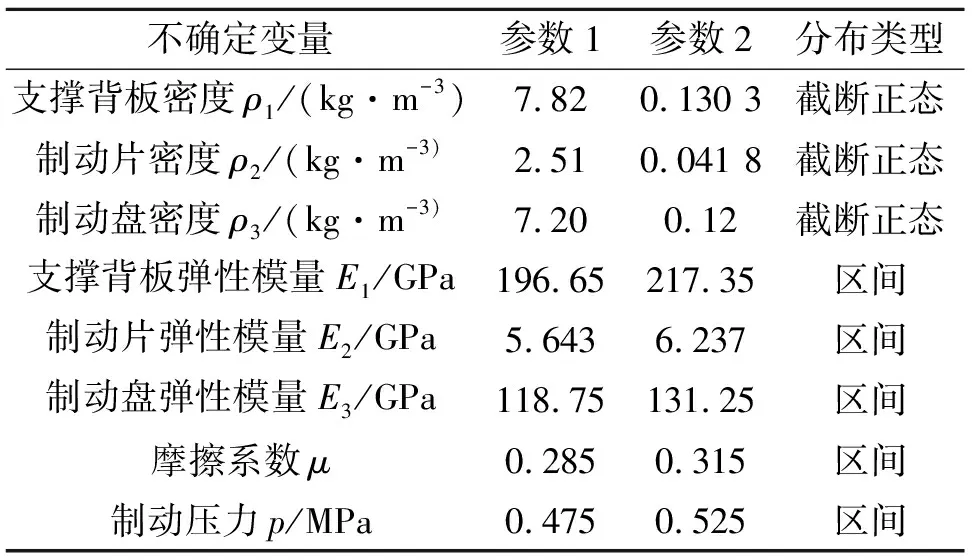
表1 制动器不确定变量分布及取值

注：在正态分布类型中，参数1为均值，参数2为标准差；在区间分布类型中，参数1为变量下界，参数2为变量上界。

采用拉丁超立方试验设计方法[13]在这些变量组成的不确定空间内采样，选取70 组样本点代入到制动器系统有限元模型中进行计算，求出0～16 kHz范围内的特征值，发现系统对应各组样本点的第7阶特征值实部均大于0，为不稳定特征值；样本点还在其他阶数上出现不稳定特征值，但其阻尼比都远比2 kHz附近的第7阶特征值小，因此本文将第7阶特征值作为首要不稳定特征值进行研究。其中某一样本点下系统的特征值分布如图3所示。

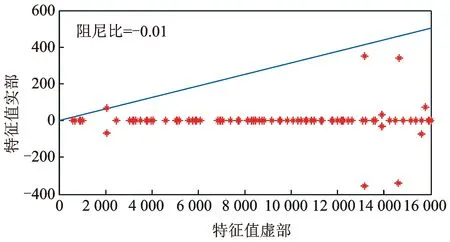
图3 某一样本下系统的特征值分布

在上述试验设计的基础上，基于二阶多项式响应面模型建立第7阶特征值参数化的近似表达式为

α7=68.19+5.69z1+6.66z2-25.31z3-1.81z4-1.24z5+9.95z6+15.6z7-1.95z8+0.42z1z2-1.76z1z3+0.34z1z4-2.10z1z5-3.25z1z6+1.51z1z7+1.39z1z8+4.87z2z3+1.04z2z4-2.88z2z5+2.04z2z6+2.17z2z7-3.34z2z8+3.36z3z4+4.66z3z5+2.49z3z6-3.11z3z7+1.31z3z8+0.62z4z5+2.48z4z6-4.19z4z7-3.37z4z8+2.87z5z6+0.77z5z7-0.91z5z8-

(30)

β7=1 965.24-67.5z1+13.9z2-137z3+39.4z4-1.24z5+98.9z6+62.9z7-20.4z8+18.3z1z2-50.9z1z3-12.1z1z4-22.9z1z5-22.3z1z6+21.2z1z7+15.3z1z8+41.7z2z3+5.23z2z4-30.7z2z5+25.9z2z6+25.9z2z7-34.0z2z8+54.1z3z4+49.2z3z5+11.8z3z6-36.0z3z7+14.0z3z8+6.52z4z5+16.0z4z6-46.4z4z7-36.2z4z8+31.3z5z6+6.98z5z7-8.67z5z8-

(31)

式中α7为第7阶特征值实部；β7为第7阶特征值虚部；z1,z2,…,z8为标准化变量。按文献[13]的方法对上述响应面模型进行显著性分析，可得响应面模型的不可靠概率小于1%，与真实有限元模型的逼近程度高，能够用于后续分析研究。

3.2 系统稳定性的可靠度分析

结合式(6)，(12)和(28)可知，系统第7阶特征值稳定的可靠度为

(32)

式中Z=(z1,z2,…,z8)为标准化向量。采用蒙特卡洛法进行30 000 次抽样分析，求得初始值下系统稳定的最小和最大可靠度分别为0%和34.4%。可见在初始不确定参数下系统稳定性极差，需要对系统的稳定性进行改进提高。

3.3 Sobol′法全局灵敏度分析

由式(32) 可知，功能函数值越大，系统稳定性越高，为了甄别各不确定参数对系统稳定性影响的大小，对所有不确定参数均匀抽样1 000 000次，采用Sobol′法计算功能函数对各标准化变量的一阶全局灵敏度及总体全局灵敏度值，结果如表2所示。

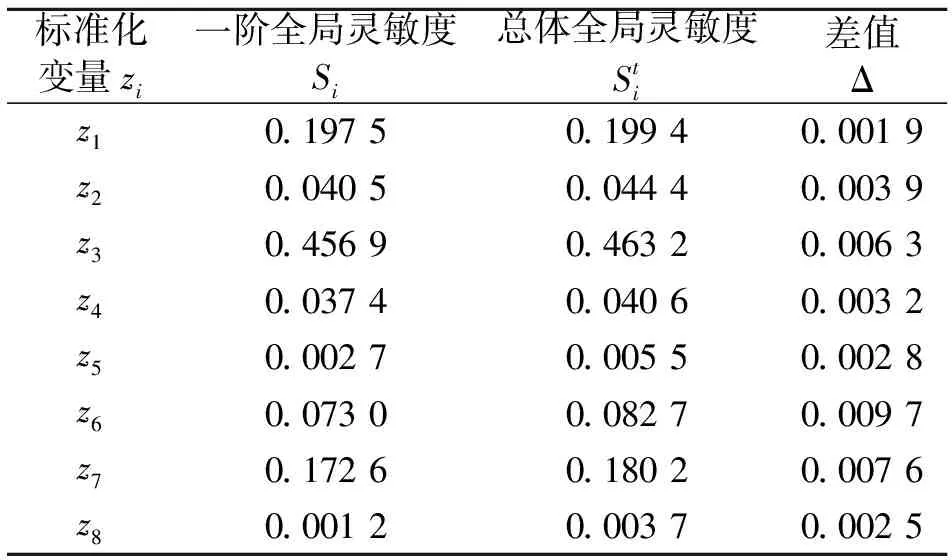
表2 标准化变量的一阶和总体全局灵敏度

为了更直观地表示出功能函数对各标准化变量的灵敏度大小，绘制灵敏度直方图如图4所示。

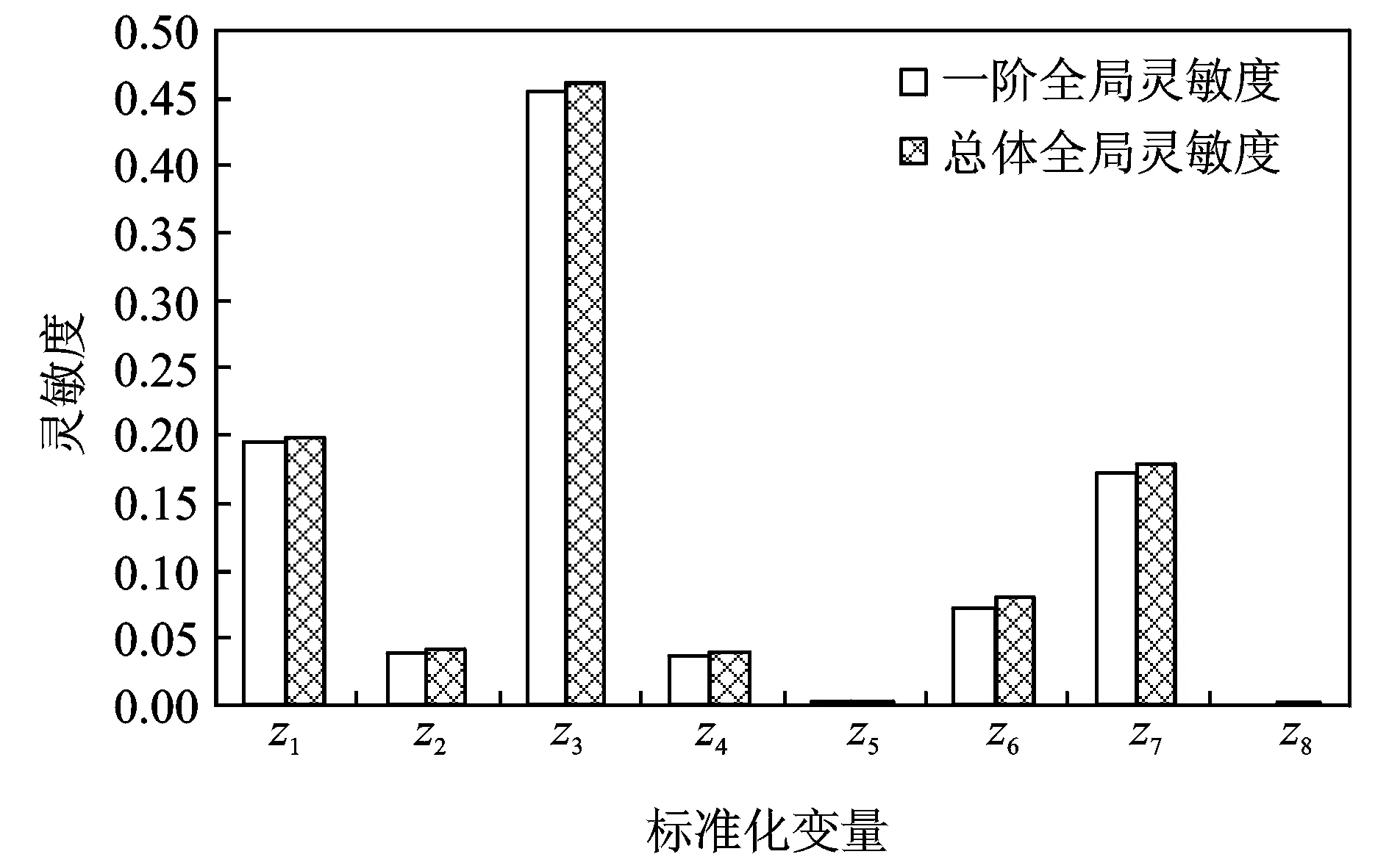
图4 标准化变量的全局灵敏度

表2中一阶全局灵敏度系数反映的是变量自身变化对结果的影响程度，总体灵敏度系数不仅反映了该变量自身变化的影响，还反映该变量与其他变量变化交互作用的影响。因此当某变量的一阶灵敏度和总体灵敏度差值较大时，可知该变量与其他变量间存在明显的交互作用。

结合表2和图4可以看出：

(1)z1,z3和z7的一阶全局灵敏度系数很高，改变这些变量对系统稳定性有较大的影响，尤其是z3的一阶全局灵敏度系数高达0.456 9，该变量单独作用时对系统稳定性有重要影响，在工程实际中应特别对其不确定性严格控制，使其波动范围尽可能小。而z5和z8的一阶全局灵敏度系数几乎接近0，对系统稳定性影响极小，工程实际中可以对其不确定性控制适当放宽，以降低成本；在分析研究中则可忽略与其对应的参数不确定性，当作确定参数进行处理，以减小分析工作量。

(2)z3,z6和z7的一阶全局灵敏度与总体全局灵敏度的差值分别达到了0.006 3，0.009 7和0.007 6，表明它们与其他变量之间存在明显的交互作用。

3.4 系统稳定性可靠度的提高

由第3.3节分析可知，z5和z8对系统稳定性几乎没有影响，而z1,z2和z3分别对应系统各部件的材料密度，一般来说材料密度在工程上很少进行修改。因此本文主要考察z4,z6和z7对系统稳定性可靠度的影响。与z4,z6和z7对应的系统参数为支撑背板弹性模量、制动盘弹性模量和系统摩擦系数，对上述系统参数选取一系列区间值进行系统稳定性分析。在针对某个参数进行分析时，其他参数的不确定性取值及分布类型同表2，所有不确定参数的波动范围仍为其均值的±5%。可靠度分析结果如表3～5所示。

由表3～5可以看出，随着支撑背板弹性模量的增大，系统稳定性可靠度随之增大；随着制动盘弹性模量增大或摩擦系数增大，系统稳定性可靠度均减小。

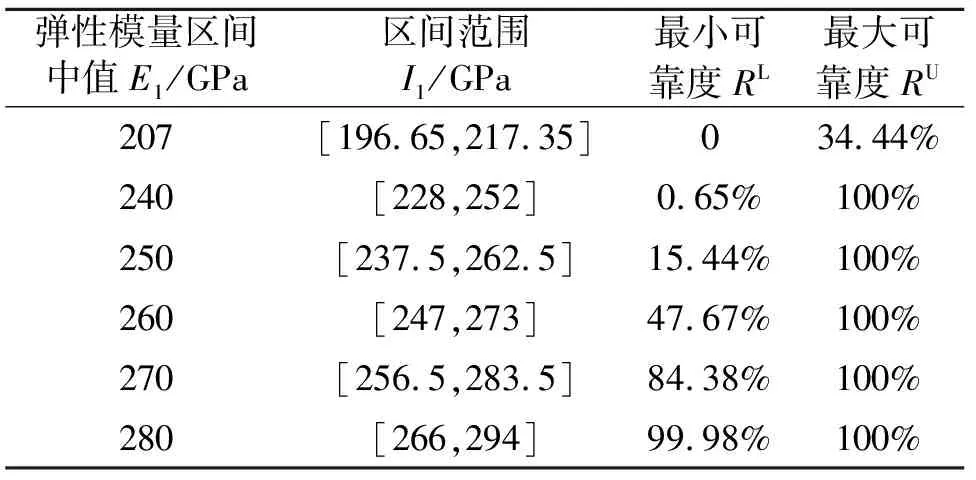
表3 支撑背板不同弹性模量下系统的稳定性

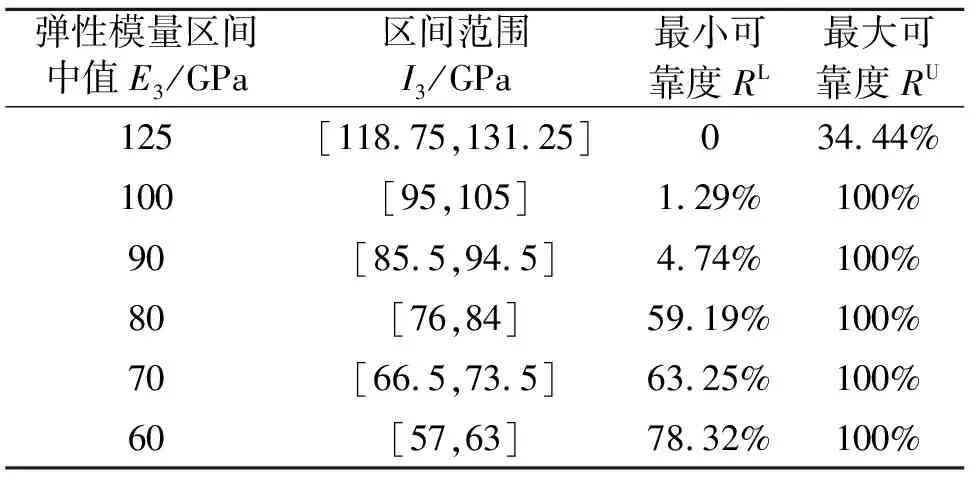
表4 制动盘不同弹性模量下系统的稳定性

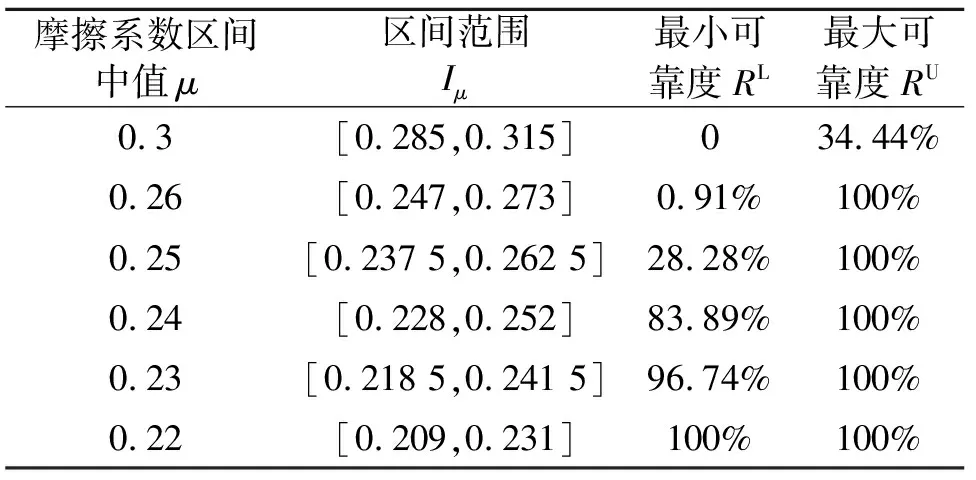
表5 不同摩擦系数下系统的稳定性

减小制动盘弹性模量以提高制动器稳定性，从结构强度和刚度角度考虑是不可取的；而摩擦系数在实际工程中是个难以掌握和控制的变量，减小摩擦系数还会严重影响制动效率，因而通过减小摩擦系数来提高制动器稳定性也不是直接有效的方法。

支撑背板既不是摩擦部件也易于更换，因而可通过提高其刚度来提高制动器稳定性，工程上可采用弹性模量更大的材料或者加大支撑背板的几何厚度等措施来提高支撑刚度，并在不改变系统摩擦系数和制动压力的情况下能使制动器制动功能得到保证。

4 结 论

(1)本文将参数不确定性引入到汽车盘式制动器振动稳定性的可靠性分析中，采用随机参数和区间参数对制动器系统进行描述，将响应面法与有限元复特征值技术相结合，实现了制动器稳定性可靠度研究模型的参数化，大大提高了可靠性分析效率。

(2)采用蒙特卡洛法研究了系统参数为正态分布随机参数和区间参数下，某型车的浮钳盘式制动器系统的稳定性可靠度，结合Sobol′法对不确定参数进行了全局灵敏度分析，甄别了不确定性参数对系统稳定性的影响，并从可靠性角度提出了改善制动器系统振动稳定性的工程措施，不确定参数的引入提高了传统研究方法的适用性，分析方法对抑制制动噪声具有一定的工程指导性。

参考文献:

[1] YANG S, GIBSON R F. Brake vibration and noise: reviews, comments, and proposals[J]. International Journal of Materials and Product Technology, 1997,12(4-6):496—513.

[2] FRITZ G， SINOU J J， DUFFAL J, et al. Effects of damping on brake squeal coalescence patterns application on a finite element modal[J]. Mechanics Research Communication，2007，34(2)：181—190.

[3] GUAN Dihua， SU Xindong， ZHANG Fang. Sensitivity analysis of brake squeal tendency to substructures′ modal parameters[J]. Journal of Sound and Vibration，2006，291(1)：72—80.

[4] 张义民.任意分布参数的机械零件的可靠性灵敏度设计[J].机械工程学报，2004，40(8)：100—105.ZHANG Yiming.Reliability sensitivity design for mecha- nical elements with arbitrary distribution parameters[J]. Chinese Journal of Mechanical Engineering，2004，40(8)：100—105.

[5] ZHANG Hao， MULLEN R L， MUHANNA R L. Interval monte carlo methods for structural reliability[J]. Structural Safety，2010，32(3)：183—190.

[6] MELCHERS R E， AHAMMED M. A fast approximate method for parameter sensitivity estimation in monte carlo structural reliability[J]. Computers and Structures，2004，82(1)：55—61.

[7] SOBOL′ I M， TARANTOLA S， GATELLI D， et al. Estimating the approximation error when fixing uncessential factors in global sensitivity analysis[J]. Reliability Engineering and System Safety，2007，92(5)：957—960.

[8] JUNIOR M T，GERGES S N，JORDAN R. Analysis of brake squeal noise using the finite element method[J]. Applied Acoustics，2008，69(2)：147—162.

[9] LIU P， ZHENG H， CAI C. Analysis of disc brake squeal using the complex eigenvalue method[J]. Applied Acoustics，2007，68(6)：603—615.

[10] SOBOL′ I M. Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates[J]. Mathematics and Computers in Simulation，2001，55(1)：271—280.

[12] JIANG Chao， HAN Xu. A hybrid reliability approach based on probability and interval for uncertain structures[J]. Journal of Mechanical Design，2012，134(3)：1—11.

[13] PAPILLA M. Accuracy of response surface approximations for weight equations based on structural optimization[D]. Gainesville：University of Florida，2001.