某牵引火炮后大架轻量化设计

张俊飞，顾克秋，付帅

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

牵引火炮的轻量化概念早在20 世纪70 年代左右已经产生，由于火炮质量直接影响其战略、战术机动性及安全性，因此有必要通过轻量化设计来提高火炮战术机动性，使其快速应对各种突发事件。针对火炮全部质量的轻量化设计(图1)，由于多种因素导致无法实现，更多的文献是采取对单独某个部件的轻量化设计则通过静力学优化来实现，这无疑与部件在火炮发射过程中产生的动态应力应变相不符。

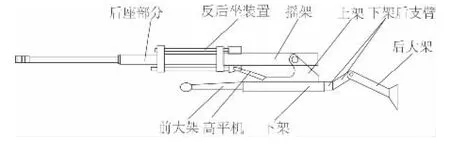
图1 轻型牵引火炮原理示意图

本文通过建立某牵引火炮刚柔混合动力学有限元参数化模型来研究后大架的轻量化，其中后大架采用柔体建模，其余部件均为刚体，在进行有限元分析的基础上，以后大架的形状和板厚参数作为优化设计变量，约束后大架的屈服极限，优化后最终获得了一组保证刚强度同时质量最轻的后大架参数，为各部件的轻量化设计提供参考。

1 全炮有限元动力学分析及参数化

1.1 刚柔混合模型有限元分析

为准确分析后大架，同时保证计算效率，采用刚柔混合建模，摇架、身管、上架、前大架及下架等均采用刚体建模，在其质心位置赋予质量及转动惯量，用Axial 连接器模拟高平机作用;后大架采用柔体建模，单元采用一阶完全积分单元离散，与下架后支臂通过两个转动副连接，自身可以分为架体和驻锄，在驻锄端面耦合参考点模拟驻锄的转动中心，然后与地面建立弹簧连接器，模拟驻锄与土壤的接触关系。

在炮尾端面施加膛底压力，模拟火药对后坐部分的载荷;在身管轴线方向建立参考点，并施加导转力矩模拟弹丸对身管膛线的扭矩作用;制退机力与复进机力则通过函数子程序二次开发编程来施加，实现数据传递。

考虑到火炮后坐阻力最大时刻全炮工况最为恶劣，因此有限元模型重点考察在火炮后坐过程中的动态应力应变。

1.2 计算结果分析

在输出的DAT 文件中得到全炮优化前初始状态的总质量为4 007.248 kg，由于只对后大架进行参数化，故可以通过全炮质量的变化值表征后大架总质量的变化程度。

后大架应力变形如图2 所示，最大应力为425.2 MPa，出现在腹板圆弧处，除去应力集中区，其他大部分区域应力均小于200 MPa。后处理中选择应力最大位置处单元节点的Mises 值输出，作为进一步优化时的约束条件。

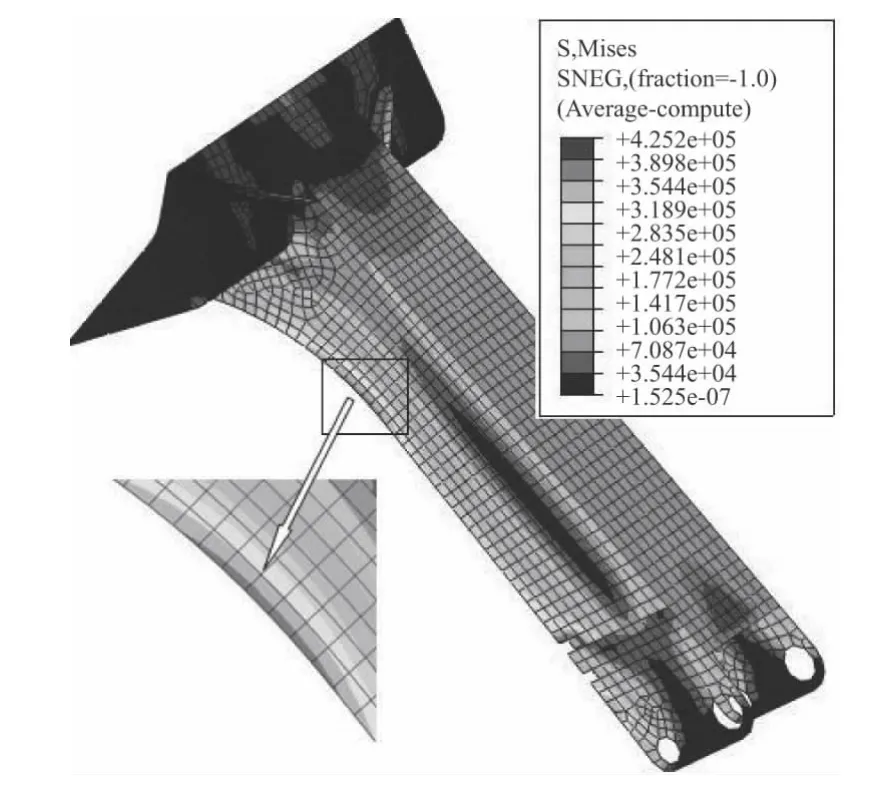
图2 后大架应力云图及Mises 最大值区域

1.3 参数化模型

用Python 语言编写有限元前处理程序，实现全炮的参数化建模，后大架参数主要分为板厚参数和形状参数两大类，改变这些参数值即可获得不同的后大架模型，同时也会生成相应的全炮模型。

后大架架体形状通过x1、x2、x3 三个参数来控制，x4、x5 两个参数可控制驻锄加强筋的布局，如图3，图4 所示。后大架参数化有限元模型各形状参数、设计上限、设计下限及参数说明如表1 所示。除了上述形状参数外，组成后大架的部分钛合金板的板厚也是优化参数，对不同部位的板厚度的合理匹配，可以在保证结构性能的前提下获得最优的结构。后大架参数化有限元模型各板厚参数、设计上限、设计下限及参数说明如表2 所示。

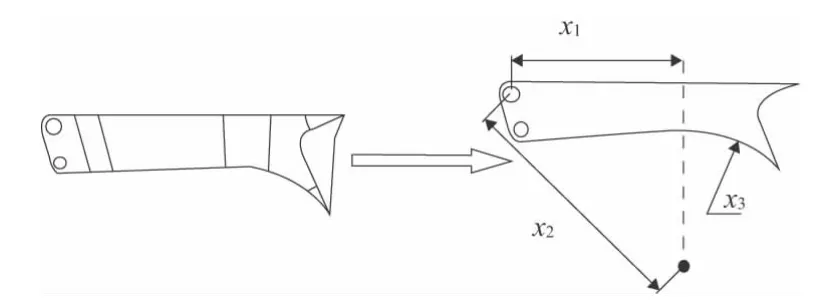
图3 后大架架体形状参数

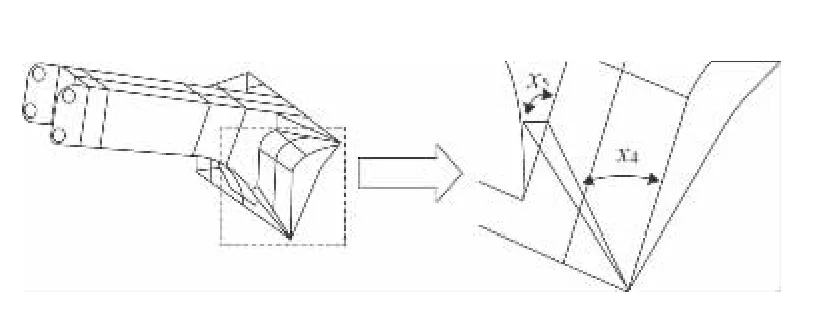
图4 驻锄加强筋形状参数

表1 后大架参数化有限元模型形状参数表

续表1

表2 后大架参数化有限元模型板厚参数表

2 试验设计及近似模型

若对全炮模型直接运用多岛遗传算法进行优化设计，至少需要上千次寻优计算，耗时过长，一轮优化至少将耗时几周的时间，显然是不现实的。对于复杂的工程问题，可采用通过实验设计采样制作的近似模型(亦称代理模型)，将原有的复杂系统结构力学模型转换成一个数学模型，使单次寻优计算时间大幅降低，优化设计效率大大提高。

本文研究的计算模型，即全炮刚柔混合动力学有限元模型兼具材料非线性、几何非线性和边界非线性，这种场合使用Kriging 模型最合适。近似模型的制作流程如图5 所示。首先通过试验设计(DOE)确定样本点，然后对这些样本点逐一进行有限元计算获得输出结果，根据输入值、输出值建立近似模型，待验证模型准确后即可用于优化计算。

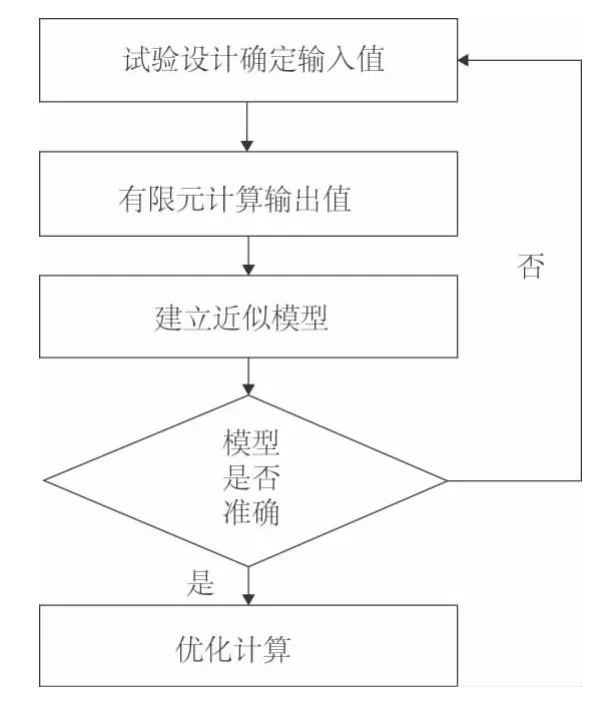
图5 近似模型制作流程图

样本点选取采用拉丁方(LHS)试验设计方法，他具有较好的散布均匀性和随机性，可用较少的样本点获得较全面的信息。

在11 个优化参数的设计范围内选取了200 个样本点构造Kriging 近似模型，经验证计算，该模型能较好地模拟复杂系统非线性有限元问题，部分样本点如表3 所示。

3 优化设计及结果

3.1 优化数学模型

将经过试验设计的Kriging 模型作为优化模型，具体数学模型描述如下:

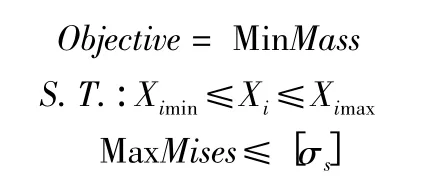
其中:MaxMises 为后大架最大应力，Mass 为全炮质量，Xi为设计参数，包括后大架形状参数和板厚参数共11 个参数，［σs］为材料许用应力，这里取720 MPa。

3.2 优化算法

遗传算法是如今广为应用的一类求解复杂全局最优化问题的仿生型优化算法。在传统遗传算法的应用过程中有一个突出的问题是，它容易产生早熟现象，这将严重地影响算法的应用效果，多岛遗传算法也是根据目标函数和约束条件对每个设计点进行评估，但不同的是，多岛遗传算法将设计种群分解为子种群，也称为“岛”，而且算法中的迁移操作保持了优化解的多样性，提高了包含全局最优解的机会，进化流程如图6 所示。

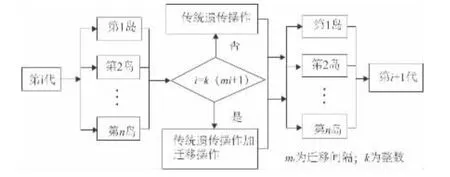
图6 多岛遗传算法进化流程

在Kriging 近似模型基础上，基于多岛遗传算法(MIGA)对全炮模型进行优化。多岛遗传算法参数设置:

1)采用二进制编码，基因长度设为32。

2)经过多次试验研究将设计空间分为10 个岛，每个岛10 个个体，群体规模为100，这个规模对本例的优化较为合适。遗传代数40 代，外迭代次数为5，故总的运行次数为20 014 步。

3)为了保证多岛遗传算法的收敛性，本文是采用最优个体保存策略的，即每代的最优个体直接保留至下一代，不参与交叉与变异操作，每个岛屿只保留1 个最优个体。

4)通过对交叉于遗传这两个遗传算子的多次试验研究，将本文的交叉概率设为0.9，变异概率设为0.01。

5)迁移间隔为5 代，迁移率为0.5。

3.3 优化结果分析

通过优化历程看出，整个寻优过程有明显的下降趋势，优化结果如表4 所示。

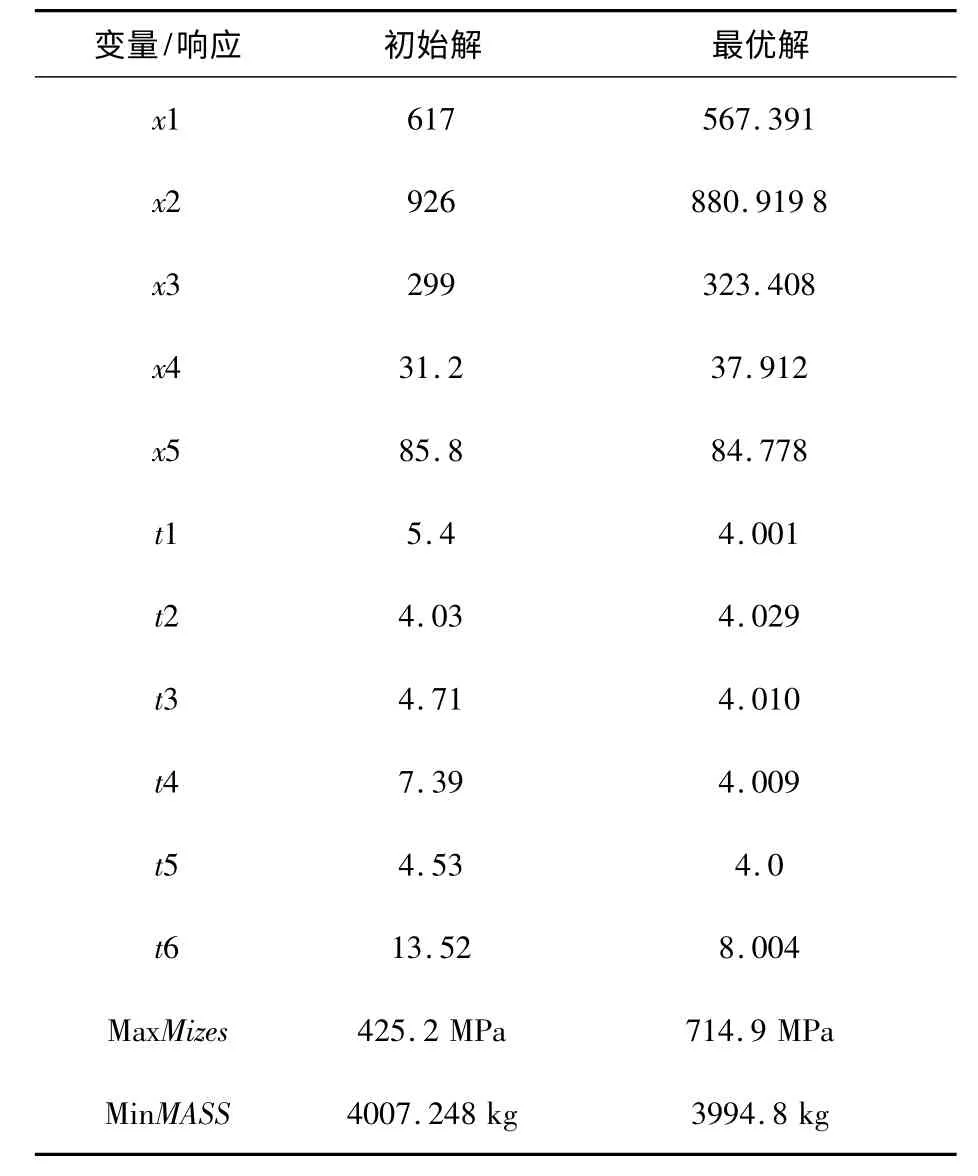
表4 基于MIGA 的后大架Kriging 模型最优解与初始解数值对比

经过多岛遗传算法优化后全炮质量减少12.5 kg，同时后大架最大应力处的Mises 值小于材料的屈服极限。由于本文仅考察后大架轻量化，故相当于优化后的后大架质量减少了12.5 kg，约占后大架优化前质量的1/4，所以优化效果明显。

4 结论

本文在建立某牵引火炮动力学有限元模型的基础上，考察基于，火炮总体发射下的后大架轻量化设计，为了提高优化效率，尝试使用近似模型代替原有限元参数化模型进行多岛遗传算法优化，得到了使全炮质量最轻的一组后大架参数最优解。

代理模型在保证与原有模型计算准确性基础上，使得一次运算历程缩短至不到1 s，从而确保了优化的可行性及结果可靠性。

从优化结果可以看出，这种通过在总体建模框架下考察某个部件轻量化的思路可行且效果明显，因此，对于其余各部件的结构设计及轻量化，该思路与方法具有一定的推广应用价值。

［1］马洪锋.迫击炮座钣结构分析与优化设计［C］.南京:南京理工大学，2009:19-29.

［2］项立银.基于组合优化算法的结构稳健优化方法研究与应用［C］.南京:南京理工大学，2011:42-51 .

［3］周成.轻量化牵引火炮动力学分析与优化研究［C］.南京:南京理工大学，2011:37-38.

［4］赵志国，司传胜.基于多岛遗传算法的铰接车轮边减速器优化设计［J］.机械设计与制造，2010(12).

［5］牟淑志，杜青江，牟福元，等.基于多岛遗传算法的连续体结构拓扑优化［J］.机械科学与技术，2009(10).