灰色残差模型在城市工业需水量预测中的运用
2014-04-01王鹏黄显峰崔延松
王鹏,黄显峰,崔延松
(1.河海大学 水利水电学院,江苏 南京 210098;2.南通大 学交通学院,江苏 南通 226019)
0 引言
水是生命之源,也是工业生产活动中不可缺的重要资源,故工业需水量预测是直接影响到一个城市工业持续稳定发展的重要工作内容[1]。现有很多常用的需水量预测方法,如ARMA 方法、回归分析法、指标分析法、灰色预测法、人工神经网络法、系统动力学方法等[2]。但很多方法和模型需要大量的历史数据资料,且对数据的要求很高,考虑的影响因子很多,各因子之间关联复杂,限制了很多方法的使用,但其中不乏简单易行的方法,例如灰色模型。
灰色模型具有建模原理简单,计算方便,所需样本少,预测精度高,不考虑影响因素和因子等特点[3-5],已成功应用到多个行业和社会领域的需求预测中。然而实践过程中得到的预测结果却不尽如人意,其原因是现实中的统计数据经常呈现出毫无规律,很难满足指数规律,这样的数据带入传统灰色模型无法满足预测精度,也无法保证预测值的可信度;再者灰色模型不适合对客观事物做长期预测,会出现系统误差。故人们越来越渴求对灰色模型进行修正和改进,来更精确地对客观事物进行长期预测。灰色残差模型正是在这样的背景下出现的一种改进的灰色模型,通过对残差序列进行修正,使预测值满足预测精度,为进行客观事物的预测工作带来了极大的便利。
1 预测模型构建原理
1.1 灰色模型原理
GM(1,1)是基于单变量一阶常微分方程建立的,被称为一阶一元灰色方程,是最普遍使用的一种灰色模型。
假设初始数据序列x(0)={x(0)(1),x(0)(2),…,x(0)(N)},令x(1)(i)=,此式所表示的数据序列为初始数据序列的一次累加而得到,可称为一次累加生成。显然有x(1)(1)=x(0)(1) 。初始数据序列按一次累加生成得出:
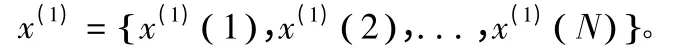
设x(1)符合一阶常微分方程:
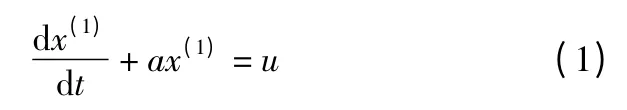
式中,a 和u 是常数,a 是发展灰数;u 是内生控制灰数,是对系统的常定输入。
此方程符合初始条件:t=t0时x(1)=x(1)( t0)的解为:
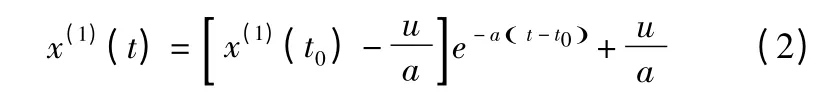
对等间隔取样的离散值(t0=1)则为:
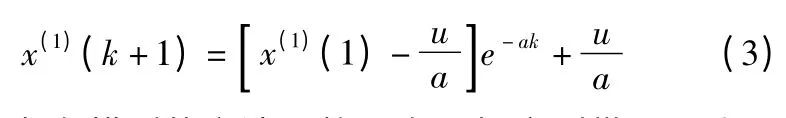
构建灰色模型的方法是将一次累加序列带入最小二乘法来求得常数a、u。
因x(1)(1) 为初值,故将x(1)(2),x(1)(3),…,x(1)(N),分别代入式(1),用差分代替微分,又等间隔取样,△t=(t+1)-t=1,故得:
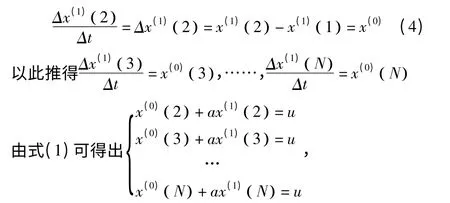
移项后转化为向量的数量积形式:
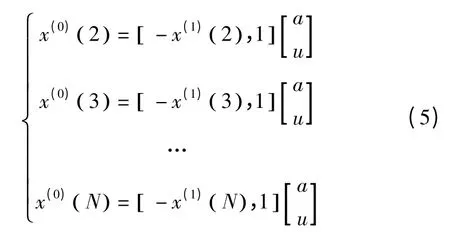
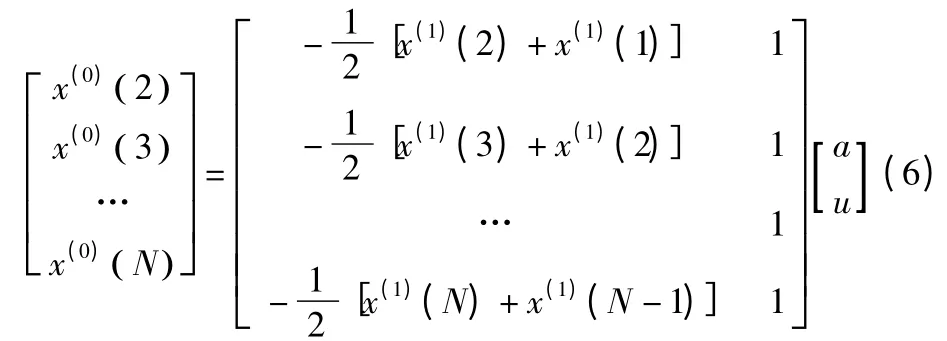
令y=(x(0)(2),x(0)(3),...,x(0)(N))T.T 表 示转置。

则式(6)可表示为矩阵形式:

式(7)的最小二乘估计为:
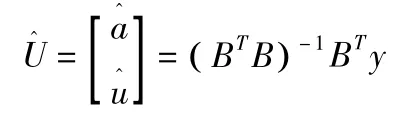
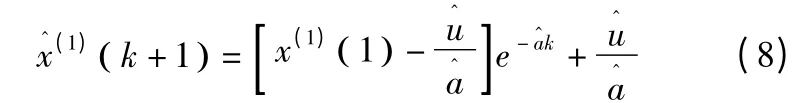
此方程为时间响应方程。
最后得到预测模型:
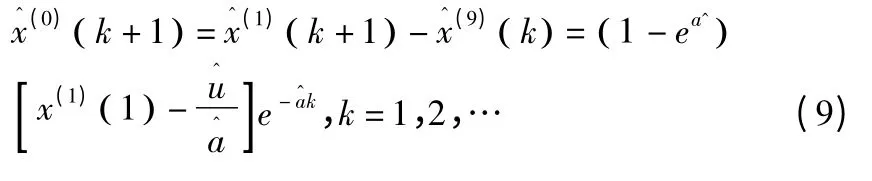
1.2 灰色残差模型原理
由灰色GM(1,1)模型计算出的模拟值与初始数据有较大差异时,即误差(或残差)较大时,可将残差序列建模,获得满意的残差序列,之后将修正后的残差模型来带入到所求得的灰色GM(1,1)模型,这种融合了残差模型及灰色GM(1,1)模型的新模型称为灰色残差模型。
将初始数据序列x(0)中代入时间响应方程,求得序列(j),j=i,i+1,……,n。可求得残差 序列e(0)={e(0)(i),e(0)(i +1),…,e(0)(n)},经一次累加生成可求得序列e(1)={e(1)(i),e(1)(i +1),…,e(1)(n)},按照灰色预测建模步骤,可求得残差序列的响应方程进行求导可得,得残差修正后的模型为:
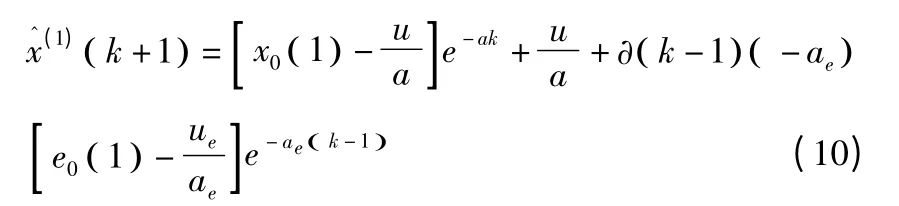
最终可求得经残差修正后的预测模型:

注:残差序列e(0)中数据必须为非负数,如果有负数存在,可进行非负处理[8],如本文选取,将其加到残差序列e(0)的各项中。
2 精度检验
精度检验包括残差检验与后验差检验,检验精度标准一般以后验差检验指标中的后验差比值C、小误差概率P作为评定指标。
2.1 残差检验
残差:E (k)=x(0)(k)-x^(0)(k),k=2,3,…,N
相对残差:
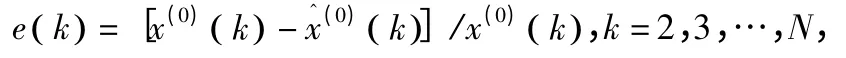
2.2 后验差检验

2.3 检验精度标准
后验差比值C 越接近0,小误差概率P 越接近1,预测精度越高,检验精度标准见表1。

表1 检验精度标准
3 南通市工业需水量预测
对南通市1998—2012 年农业用水量进行分析核实的如表2 资料(以下单位均为亿m3)。
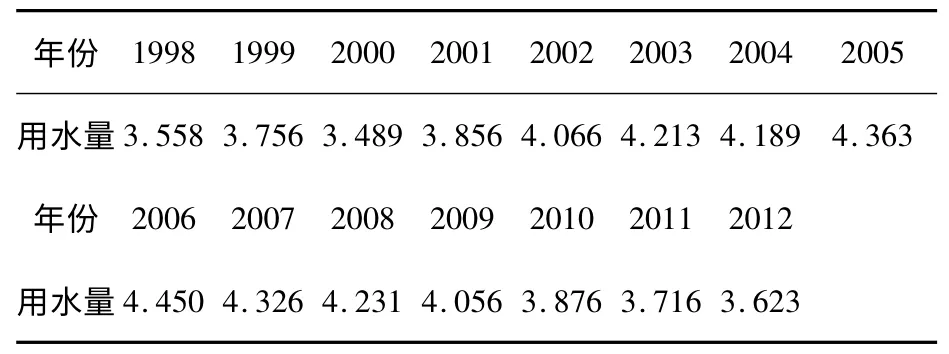
表2 南通市工业需水量1998~2012 年统计数据
3.1 建立灰色预测模型
以1998~2012 年工业用水量数据作为原始序列x(0),经一次累加生成x(1),由式(6)可求得B 和y,用最小二乘估计求出,可得时间相应方程:
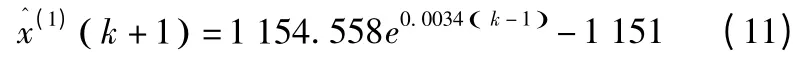
由后减还原可得预测值模型为:
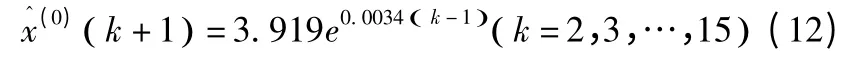
依据式(12)计算得到1999 年~2012 年的用水量模拟值见表3。
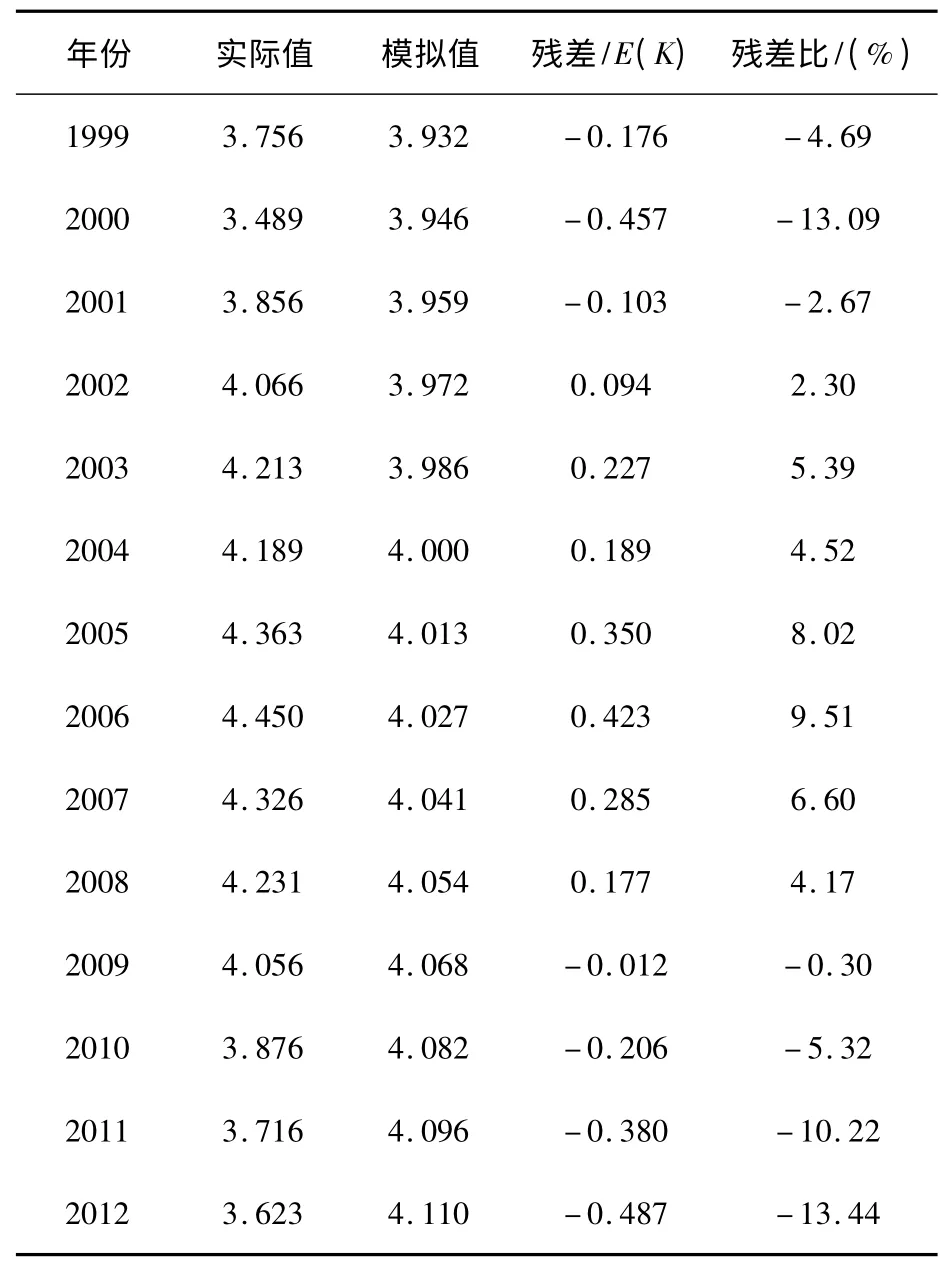
表3 GM(1,1)模型预测及精度分析
将表2 中数据带入精度检验公式,得P=0.57,C=0.968,检验精度等级为“不合格”,未达到预测精度要求,故不能进行南通市未来年份工业用水量预测。
3.2 建立灰色残差预测模型
建立灰色残差模型,首先选择残差序列e(0)中的尾端的7个数据作为原始数据,即{0.423,0.285,0.177,-0.012,-0.206,-0.380,-0.487},由于残差序列中存在负数,故应做非负处理,处理之后的序列经一次累加生成x(1),由式(6)可求得B 和y,用最小二乘估计求出,可得残差序列的时间相应方程:

由后减还原得修正后的残差值:
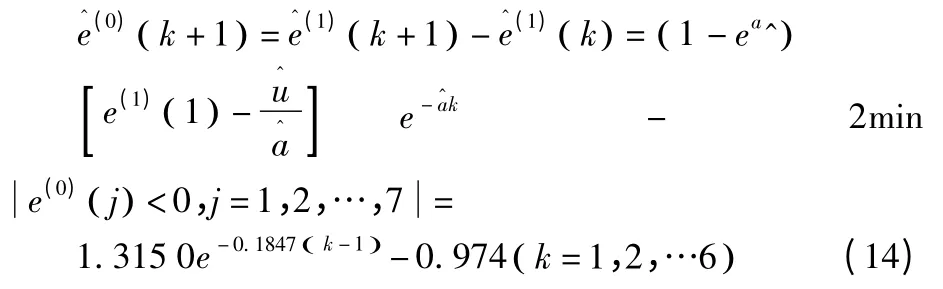
将式(12)和式(14)带入到式(10)中,最终得到灰色残差修正模型下的预测值:
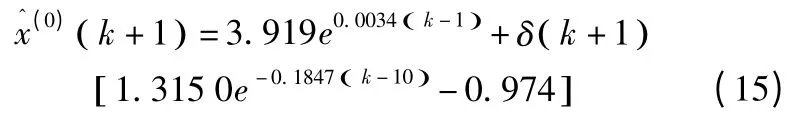
由残差模型模拟出的2006—2012 年这7 年数据通过精度检验,可得P=1,C=0.152。检验精度等级为“好”,所以灰色残差模型可作为南通市工业需水量预测模型。通过式(15)计算得南通市未来5 年内工业需水量见表4。
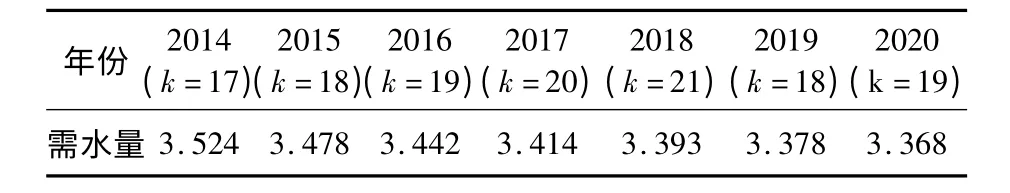
表4 灰色残差模型预测2014—2020 年南通市工业需水量
4 结果分析
灰色残差模型采用的数据是2006—2012 年南通市工业需水量,由于2006 年数据留作初值,故选取其余6 年的模型下的模拟值及其检验精度与灰色模型做分析比较,分析结果见表5,表6。
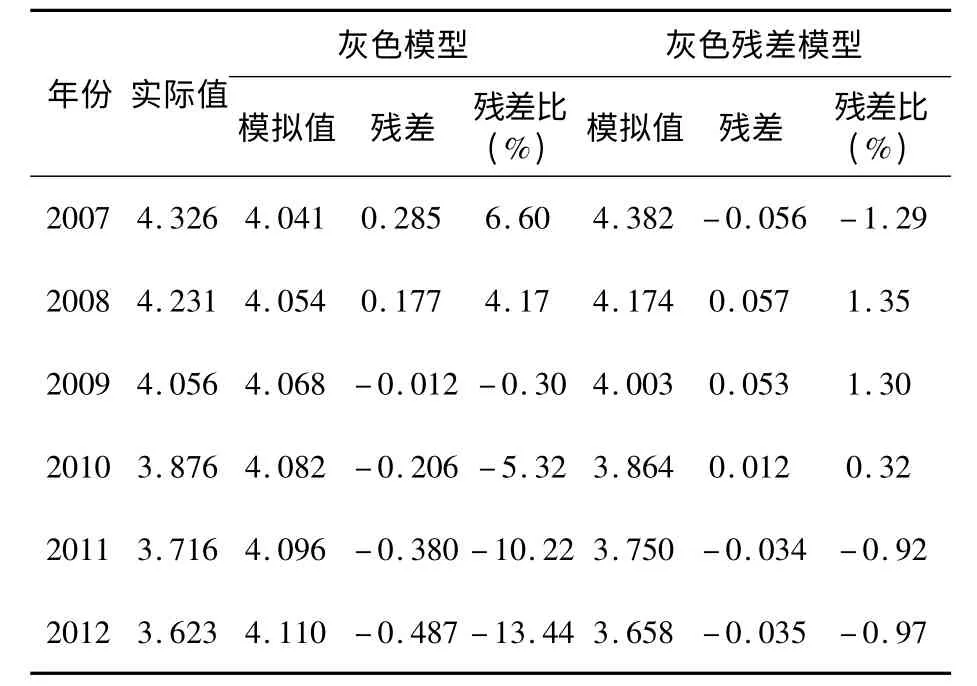
表5 两种模型下预测值与误差分析比较
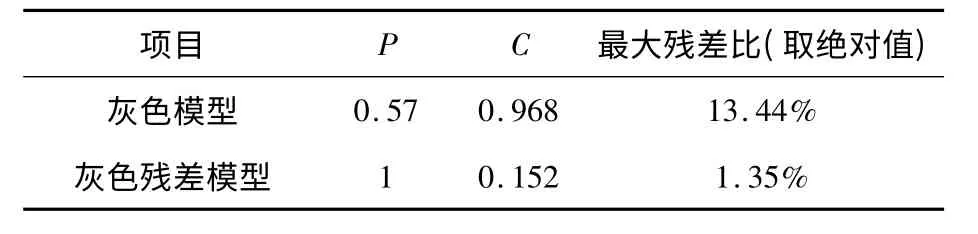
表6 预测精度对比
从上述比较中可看出,灰色残差模型的各项预测精度指标均优于灰色模型,其预测精度等级为“好”,而灰色模型预测精度等级为“差”。
5 结论
1)工业需水量受工业产值、产品结构、工业用水重复利用率、工业用水价格、工业技术进步指数、政策性节水率、中水回用情况以及时间等因素的制约[9-10],变化较为复杂。因此,要想将所有影响因素一一罗列出来,并给出这些因素与需水量之间准确的函数关系十分困难[11]。而灰色模型预测出的需水量是呈指数变化的,总趋势单调上升或下降,故此灰色模型中出现较大的残差。
2)即使在原始数据变化较大的情况下,灰色残差模型还是显著地减小了灰色模型下的模拟值和实际值之间的残差,使灰色模型达到满意的预测标准,所以灰色残差模型的适用范围要更广。但有时灰色残差总不一定将能误差减小到理想的范围内,满足预测精度标准,故现在出现了很多组合模型[12]结合了灰色等维递补理论[13]或灰元[14]理论等,以其各自的特点来相互弥补各自的不足,同时配合残差模型减小残差,以求满足预测精度。可以说灰色残差模型的出现为灰色模型的应用提供了更广阔的空间。总之,灰色残差需水量预测模型为今后城市水资源综合规划和供水计划的制定提供了极大的帮助。
[1]席洋,程水源,郭秀锐,等.灰色预测模型在城市需水量预测中的应用[J].环保科技,2007,13(1):25-29.
[2]张雅君,刘全胜.需水量预测方法的评析与择优[J].中国给水排水,2001,17(7):27-29.
[3]杨建飞,刘俊民,陈琳.基于灰色残差模型的灌区地下水最小埋深预测[J].人民黄河,2011,33(7):101-105.
[4]傅金祥,潘海宾,马兴冠.灰色残差模型与递补模型对比及在城市需水量预测中的应用[J].给水排水,2008,34(6):111-113.
[5]刘跃辰,王秋兵,钱凤魁,等.灰色模型与回归模型在农用地基准地价评估中的比较分析[J].农业工程学报,2010,26(Supp2):344-348.
[6]邓聚龙.灰色预测与决策[M].武汉:华中理工大学出版社,1991.
[7]崔延松,鲁红卫,曹阳,等.贵州省工业需水量预测研究[J].中国水利,2014(6):31-33.
[8]李刚,黄同愿,闫河,等.公路交通预测的灰色残差模型[J].交通运输工程学报,2009,9(5):88-93.
[9]汪妮,孙博,张刚.改进的灰色模型在城市工业需水量预测中的应用[J].西北大学学报:自然科学版,2009,39(2):313-316.
[10]张雅君,刘全胜.北京工业需水量的多元回归分析及预测[J].给水排水,2002,28 (11):53-55.
[11]王兵,王伯铎,林积泉,等.高等学校污水再生利用的途径与效益研究[J].西北大学学报:自然科学版,2007,37 (2):322-325.
[12]梁学玉,张鑫,孙天青.组合灰色预测模型在城市用水量预测中的应用[J].人民黄河,2010,32(4):79-80.
[13]胡德秀,杨杰.城市需水量的灰色非线性预测[J].陕西水力发电,1999,15(1):23-27.
[14]周振祥,周芳,等.维灰色递补模型在GDP 预测中的应用[J].黄冈师范学院学报,2011,6(31):27-28.
