地铁车门故障模式的可靠性评估

夏军，任金宝

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

车门作为地铁列车的关键子系统之一，其高故障率已经引起车门设计单位和地铁运营公司的高度重视。而可靠性研究已经成为现代产品研发和维修中的重要环节，因此对车门系统进行可靠性评估以找出设计中的薄弱环节，协助地铁运营单位制定合理的维修决策显得势在必行。

为对产品进行可靠性评估找出危害性较大的故障模式，中外学者已经做出了许多努力。尚葳蕤等［1］将基于模糊综合评判的FMECA 应用于自动装载传输系统的故障模式可靠性评估;李华府等［2］用逼近理想点法TOPSIS(technique for order performance by similarity to ideal solution)理论对某产品壳体组合加工过程部分工序的故障模式进行可靠性分析;朱小娟等［3］提出应用故障树分析方法对地铁车门系统进行故障模式可靠性评估。

目前尚未检索到将模糊TOPSIS 理论应用于地铁车门故障模式可靠性评估的研究文献。故本文引入模糊理论构建模糊TOPSIS，并应用于地铁车门故障模式的可靠性评估中。在对风险因子进行模糊评估的基础之上，利用模糊TOPSIS 得出车门系统各个故障模式的相对贴进度，进而对故障模式危害性进行排序，找出了地铁车门系统的薄弱环节，为车门的维修决策提供技术支持。

1 地铁车门简介

车门系统主要由承载导向装置、基础部件、电气控制装置和驱动锁闭装置等子系统组成，其中承载导向装置主要由长短导柱、上下导轨和携门架等组成，基础部件包括胶条、指示灯和门叶等，电气控制装置主要由EDCU、行程开关和车门控制按钮等组成，驱动锁闭装置包括电机、丝杆螺母副和带轮等，地铁车门系统的工作原理如图1所示。

车门系统的运动由电子门控器EDCU 控制、电动机驱动。EDCU 在接收到开门信号后，控制驱动电机动作，电机通过带轮带动丝杆螺母副，引起携门架、长导柱、挂架、下滚轮导向部件的动作，并最终使得门叶在导向系统的引导下向外做摆出运动。在达到完全摆出状态后，导向系统控制门叶的直线平移，使门叶平行于车辆侧面运动。在平移过程中，携门架使门叶沿着长导柱自由滑动，直到门叶达到完全打开状态［4］。

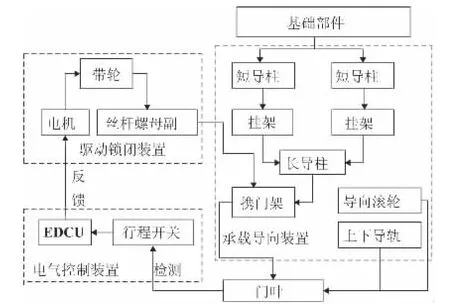
图1 地铁车门工作原理图

2 模糊TOPSIS 原理及数学模型

在传统车门可靠性评估中，需要对发生度(O)、严重度(S)和难检度(D)进行准确打分，但由于车门故障数据的缺乏，对此三个风险因子准确打分十分困难，存在较大的模糊性和不确定性，而引入模糊理论则可以用合适的语言变量及模糊数代替准确值对风险因子进行评价，解决传统可靠性评估中风险因子评价的模糊性与不确定性，使评估结果更具正确性。同时，TOPSIS 方法是一种多属性决策方法，它可以克服传统可靠性评估中风险因子相乘及风险因子无权重的问题，为可靠性评估和危害性的权衡比较提供科学的参考依据，故本文将模糊理论引入TOPSIS，构建模糊TOPSIS 理论，以对车门故障模式进行可靠性评估。

TOPSIS 方法由Hwang 和Yoon 于1981 年首次提出，是一种逼近理想方案的序数偏好方法，根据评价对象与正负理想方案的相对贴近度进行相对优劣的评价［5］，模糊TOPSIS 的识别原理框图如图2 所示。

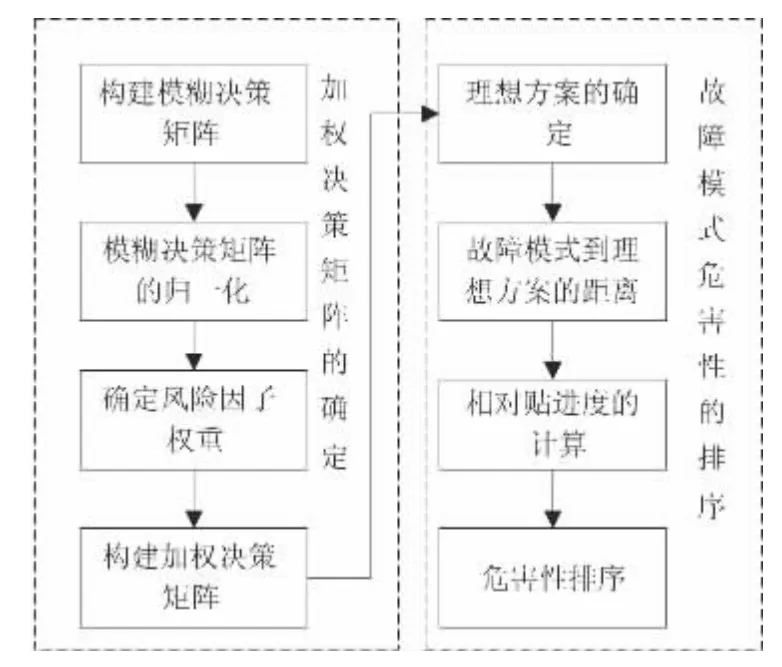
图2 模糊TOPSIS 识别原理框图

2.1 加权决策矩阵的构建

1)构建模糊决策矩阵

本文中引入模糊理论与TOPSIS 结合形成模糊TOPSIS 理论，引入模糊理论便于专家对风险因子进行评价，避免了评价时需给出准确值的缺点，使得评价更具合理性和可操作性。建立发生度(O)、严重度(S)和难检度(D)三个风险因子评价等级的语言变量与三角模糊数的对应关系，如表1 所示［6］。

表1 评价指标语言变量及三角模糊数

假设可靠性评估小组专家数量为K，用X={x1，x2，…，xn}表示故障模式集，A={a1，a2，a3}表示故障模式O、S 和D 所构成的风险因子集，故障模式xi对风险因子aj的评价值用ij来表示，对于n 个故障模式的决策矩阵可表示［7］:

2)模糊决策矩阵的归一化

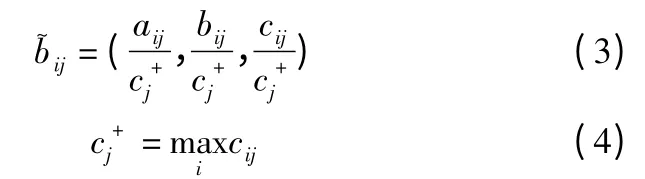
3)确定风险因子权重

对各个风险因子进行评估时，专家的主观判断通常具有模糊性，因此本文利用模糊AHP 方法对三个风险因子进行权重确定。为使专家能充分表达其主观判断的评估值，运用三角模糊数表示风险因子比较变量，如表2所示［9］。

表2 风险因子重要性比较变量及三角模糊数

构造判断矩阵:

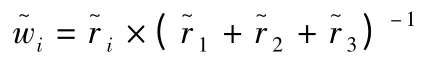
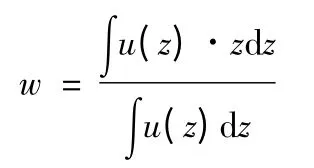
4)构建加权决策矩阵

结合归一化的决策矩阵B=(bij)nx3和风险因子的权重W=(w1，w2，w3)T，求加权决策矩阵

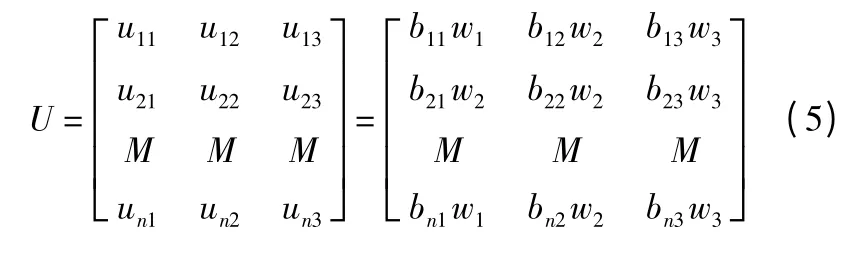
2.2 故障模式危害性的排序

1)理想方案的确定

危害性正理想方案是故障模式危害性达到最小的方案，而危害性负理想是故障模式危害性达到最大的方案。如果有一个故障模式最接近危害性负理想方案，同时又最远离危害性正理想方案，则该故障模式的危害性最大［10］。

将所有故障模式的正负理想方案确定如下:

危害性正理想方案为X+=(M1+，M2+，M3+)，

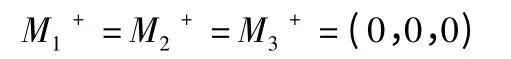
危害性负理想方案为:X－=(M1－，M2－，M3－)，

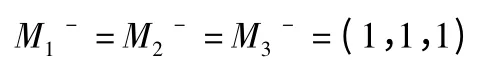
2)故障模式到理想方案的距离

每个故障模式到危害性正理想方案X+的距离为:

第一种类型，即“批评与自我批评要经常开展，让咬耳朵、扯袖子，红红脸、出出汗成为常态”[2]。这种类型的监督执纪特征：监督、执纪的对象从行为上说是党员轻微的不适当行为，即行为没有违纪但有违纪的苗头或倾向；执纪的手段或方式是“咬耳朵、扯袖子”式的而且要达到“红红脸、出出汗”效果的批评教育；监督执纪运用的理想状态是“常态”化，即这种监督、执纪应经常性、普遍性开展，被提醒、被教育的党员人数相对其它三种类型都要多。这一形态针对的对象是具有违纪倾向、苗头性问题的党员，处理原则是按照党性标准加以提醒、教育、批评、管理，以防止一些倾向性、苗头性问题发展实质性问题。

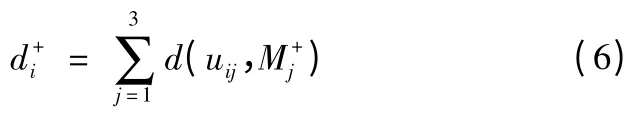
每个故障模式到危害性负理想方案X－的距离为:

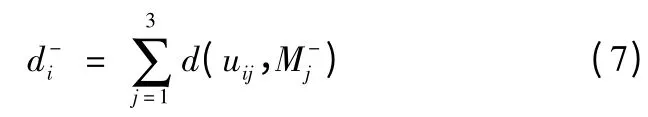
式中，d(..，..)是两个模糊数之间的距离测度。设A=(a1，a2，a3)和B=(b1，b2，b3)是两个三角模糊数，则A 和B 之间的距离测度的计算公式为:

3)相对贴近度的计算

4)危害性排序

按di值从小到大进行排序，di值越小，则对应的故障模式的危害性越大。

3 实例分析

本文对某地铁公司某车辆段28 列车18 个月的正线运营和检修中记录的车门故障信息进行统计分析，选取车门系统故障率较高的10 个故障模式利用模糊TOPSIS 进行可靠性评估，选取的地铁车门故障模式如表3 所示。

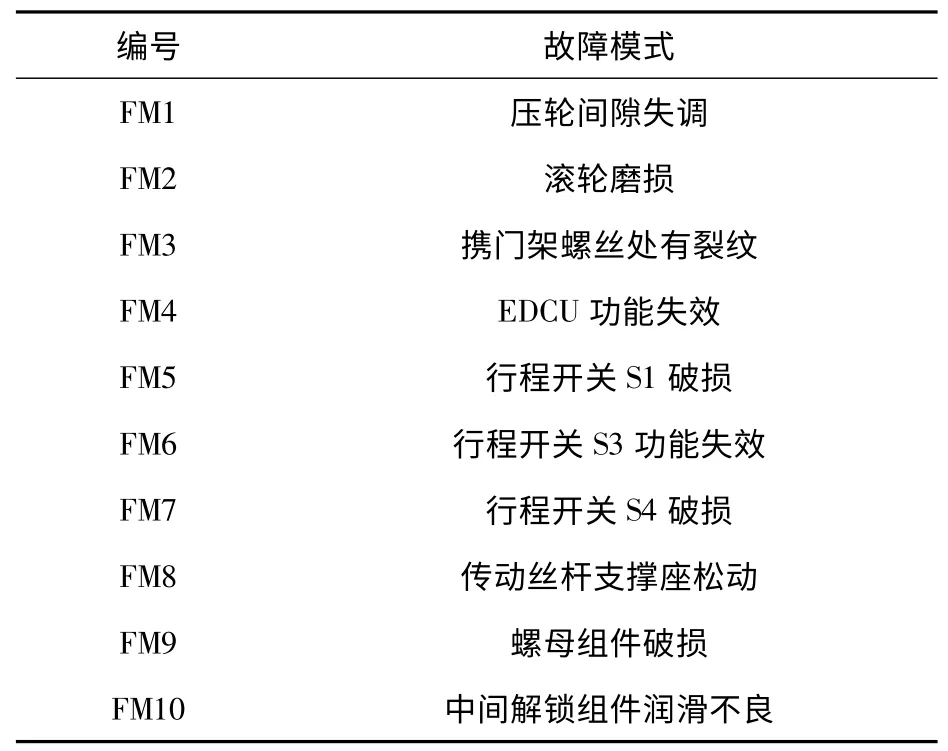
表3 车门系统常见故障模式

可靠性评估小组由5 名来自设计、装配与维修等不同部门的专家组成，对10 个故障模式的风险因子的模糊评价如表4 所示。根据式(1)，可以得知车门10 个故障模式的风险因子的综合模糊评价信息如表5 所示。根据式(2)可以得到10 个故障模式的模糊决策矩阵为:

利用模糊AHP 方法对风险因子进行权重分析。根据5 个专家分别给出的判断矩阵，根据公式进行整合，可以得知三个风险因子的模糊权重分别为:

对模糊权重去模糊化并归一化得到三个风险因子的权重为:

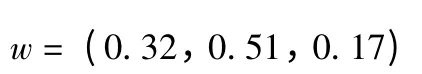
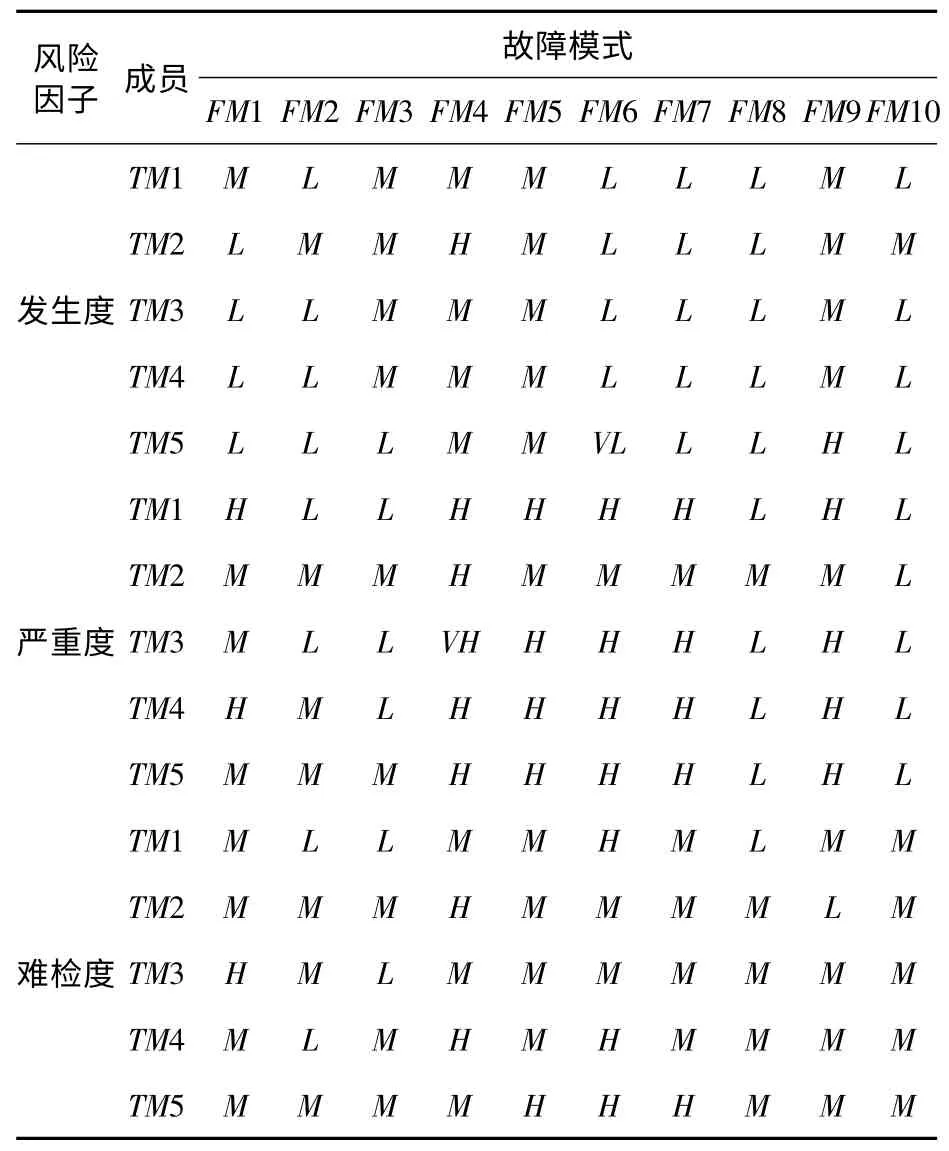
表4 车门系统故障模式风险因子模糊评价

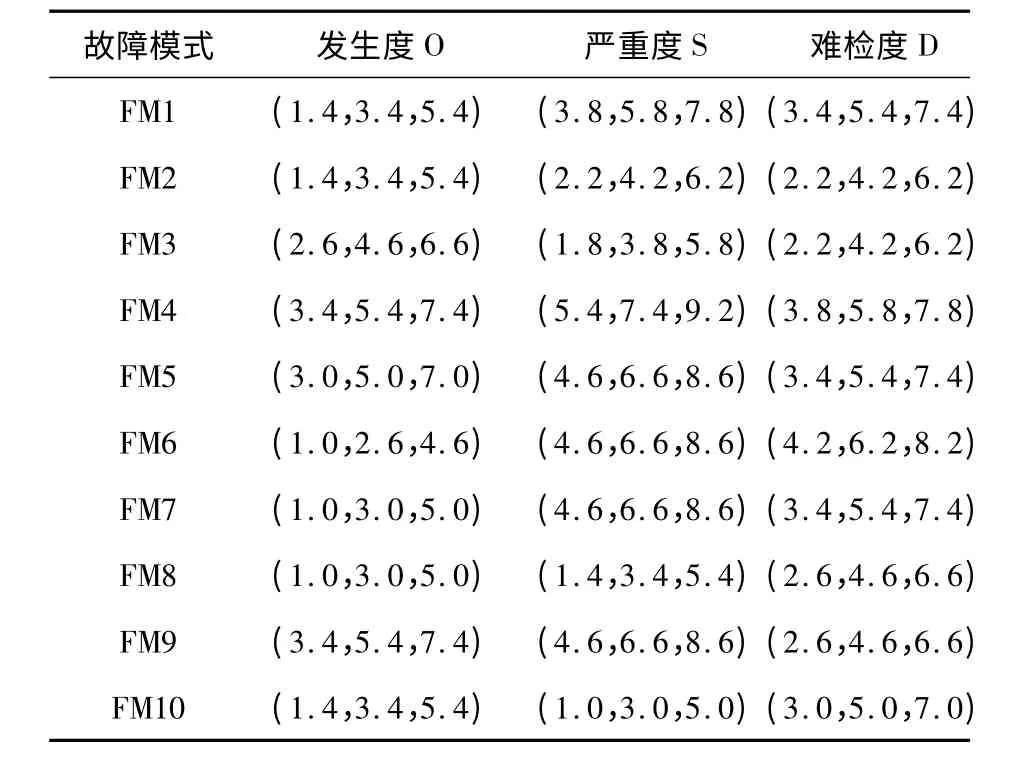
表5 故障模式综合模糊评价信息

利用式(3)和式(4)对模糊决策矩阵进行归一化，并根据式(5)和所得的风险因子权重，可以得到车门系统10个故障模式的加权决策矩阵:

根据式(6)、式(7)、式(8)计算每一个故障模式到危害性正理想方案和负理想方案的距离，如表6 所示。

根据式(9)计算相对贴进度，得到10 个故障模式的相对贴近度和危害度排序如表7 所示。

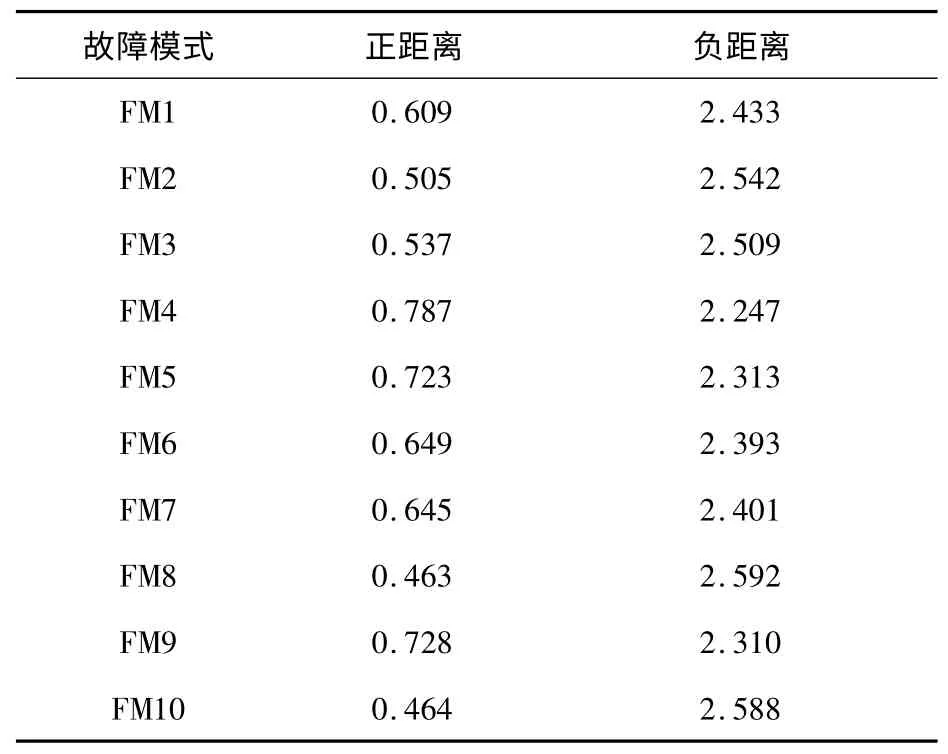
表6 故障模式到理想方案的正负距离

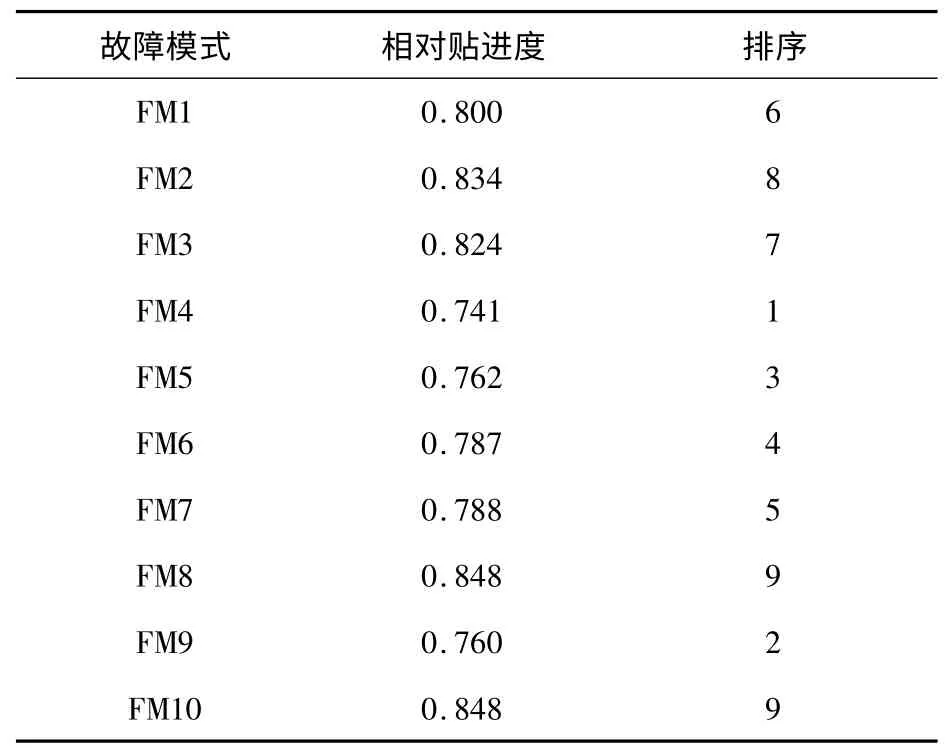
表7 车门系统故障模式危害度排序

由表7 可以得知10 个故障模式对车门系统危害性从大到小依次为:4(EDCU 功能失效)、9(螺母组件破损)、5(行程开关S1 破损)、6(行程开关S3 功能失效)、7(行程开关S4 破损)、1(压轮间隙失调)、3(携门架有裂纹)、2(滚轮磨损)、10(中间解锁组件润滑不良)和8(传动丝杆支撑座松动)。此外，EDCU 功能失效、螺母组件破损和开关S1 破损三种故障模式的相对贴进度远小于其他几种，应视为影响车门系统可靠性的关键，应重点进行可靠性设计改进并在日常维修中重点关注。另外，也应结合实际维修情况，对行程开关S3 功能失效和S4 破损、压轮间隙失调、携门架有裂纹和滚轮磨损等故障模式采取相应的改进措施。

4 结语

利用模糊TOPSIS 理论进行可靠性评估程序简便、易于操作，具有较好的合理性和适用性，在工程应用上可以作为传统可靠性评估方法的补充。本文应用模糊TOPSIS理论对车门系统故障模式进行可靠性评估，得知EDCU 功能失效、螺母组件破损和行程开关S1 破损等3 个故障模式对车门系统具有较大的危害性，应得到维修部门的重点关注。该评估结果与现场实际检修工程师经验保持一致，验证了本文方法的有效性，将为地铁车门的改进设计与维修决策的制定提供技术支持。

［1］尚葳蕤，戴忠健，侯朝桢.基于模糊综合评估的嵌入式系统FMECA［J］.计算机仿真，2006，23(10):53-56.

［2］李华府，任羿，曾声奎，等.基于TOPSIS 的故障模式危害性决策方法研究［J］.兵工自动化，2008，27(11):90-92.

［3］朱小娟，王建兵，印祯民.上海地铁车辆客室车门可靠性技术研究［J］.城市轨道交通研究，2010，(3):31-34.

［4］朱士有，吕劲松.车辆检修工［M］.北京:中国劳动社会保障出版社，2011.

［5］Ahmet Can Kutlu，Mehmet Ekmekcioglu.Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP［J］.Expert Systems with Applications，2012，(39):61-67.

［6］Chen，C.T.Extensions of the TOPSIS for group decision-making under fuzzy environment［J］.Fuzzy Sets and Systems，2000，(114):1-9.

［7］李金秋，于晶贤，苗晨.基于模糊AHP 与模糊TOPSIS 的人才选拔方案［J］.辽宁石油化工大学学报，2012，32(4):88-91.

［8］Tien-Chin Wang，Tsung-Han Chang.Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment［J］.Expert Systems with Applications，2007，(33):870-880.

［9］王娟茹.基于模糊AHP 和TOPSIS 的企业知识吸收能力评价［J］.工业工程，2010，13(3):105-110..

［10］陈军，张会生，张继光.基于TOPSIS 理论的导弹武器系统性能评估［J］.计算机仿真，2010，27(9):83-87.