基于EMD和LS-SVM的复合地基沉降预测

张丽华,刘海波,郭金鑫

(1.华北科技学院建筑工程学院，河北 三河 065201；2.中基发展建设工程有限责任公司,北京 101300)

近年来对高层建筑物复合地基沉降预测的研究文献很多，其原因主要是复合地基沉降计算的相关理论尚不够成熟。因此，基于施工阶段的复合地基沉降观测数据，应用各种预测模型对复合地基的最终沉降进行预测，对高层建筑物的安全稳定控制具有重要的作用和意义。对沉降曲线进行拟合方法常用的有双曲线法和指数曲线法，这类模型方法存在不足之处，如双曲线法预测的数值偏于保守、指数法预测初期沉降量误差较大[1-3]。时间序列预测模型适用于短期预测，长期预测精度不高[4-6]；灰色预测模型对随机扰动因素的影响预测精度不高[7-9]、；神经网络预测模型需要足够的有效数据训练样本，神经网络层次结构选择影响预测精度[10-11]；支持向量机预测模型在小样本数据预测方面具有优势，但如何构造样本数据对预测精度影响很大[12-13]。

考虑到复合地基沉降数据的特点，只用单一的预测模型不能准确地预测复合地基全过程沉降数据变化的规律。因此，很多研究表明，组合预测模型对复合地基沉降量特性的描述更加全面准确，有效提高了复合地基沉降量的预测精度[14]。很多组合预测模型建立在小波变换的基础上[15]，分解层数和小波基选择困难。EMD(经验模式分解)属于自适应小波分解。SVM(支持向量机)具有泛化能力强的优点。

根据复合地基全过程沉降数据序列的特点，结合EMD和LS-SVM两种方法的优点，提出了基于EMD和LS-SVM复合地基沉降预测方法，对复合地基全过程沉降量进行了预测和仿真，验证了模型可行有效，预测精度很高。

1 基本原理

1.1 EMD算法

EMD算法是将原始数据信号分解为若干个具有与原始信号不同局部特征信息的本征模函数(IMF)，从而实现非线性向线性、非平稳向平稳处理的转化[16-17]。

设任意一个信号为h(t)，分别用三次样条插值对该信号所有的极大值和极小值进行拟合，形成上、下包络线，上下包络线均值为m(t)，则有一新的信号，见式(1)。

g(t)=h(t)-n*m(t)n∈N

(1)

当g(t)满足局部极值点和包络线均值两个条件时，则g(t)即为第1个IMF分量c1。设r(t)为信号的余项，则如式(2)所示。

r(t)=h(t)-g(t)

(2)

将r(t)看成g(t)，不断重复(1)式，则可分别得到c2，c3…,cm，其中m∈N，为本征模函数个数。最终第m个信号余项r(t)函数应满足单调或单极值点条件。这样信号就可以表达为式(3)。

(3)

1.2 最小二乘法支持向量机的原理

LS-SVM的原理如下[18]：设n组样本数据(xi,yi)，i∈(1,2,…n)，xi∈Rn，yi∈R，分别为样本输入和输出，则可估计其最优的逼近回归函数为式(4)。

f(x)=ϖTφ(x)+b

(4)

如果其符合结构风险的最小化，见式(5)。

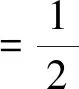
(5)

则目标方程即可转化为式(6)。

yi=ϖTφ(x)+b+ei

(6)

式中γ为惩函数，ϖ∈R为权重，b为偏置，ei(i=0,1,2,…,N)为误差。

由式(6)即可将目标优化的问题转变成拉格朗日函数，见式(7)。

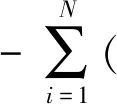
(7)

式中：αi即拉格朗日乘子。

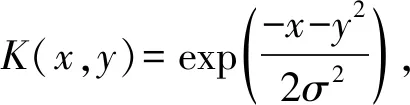
(8)

2 基于EMD和LS-SVM组合预测模型

组合预测流程图见图1。由于分解后的每个IMF分量对最终预测结果的贡献率不同，故使用SVM方法实现最优化的加权组合预测。

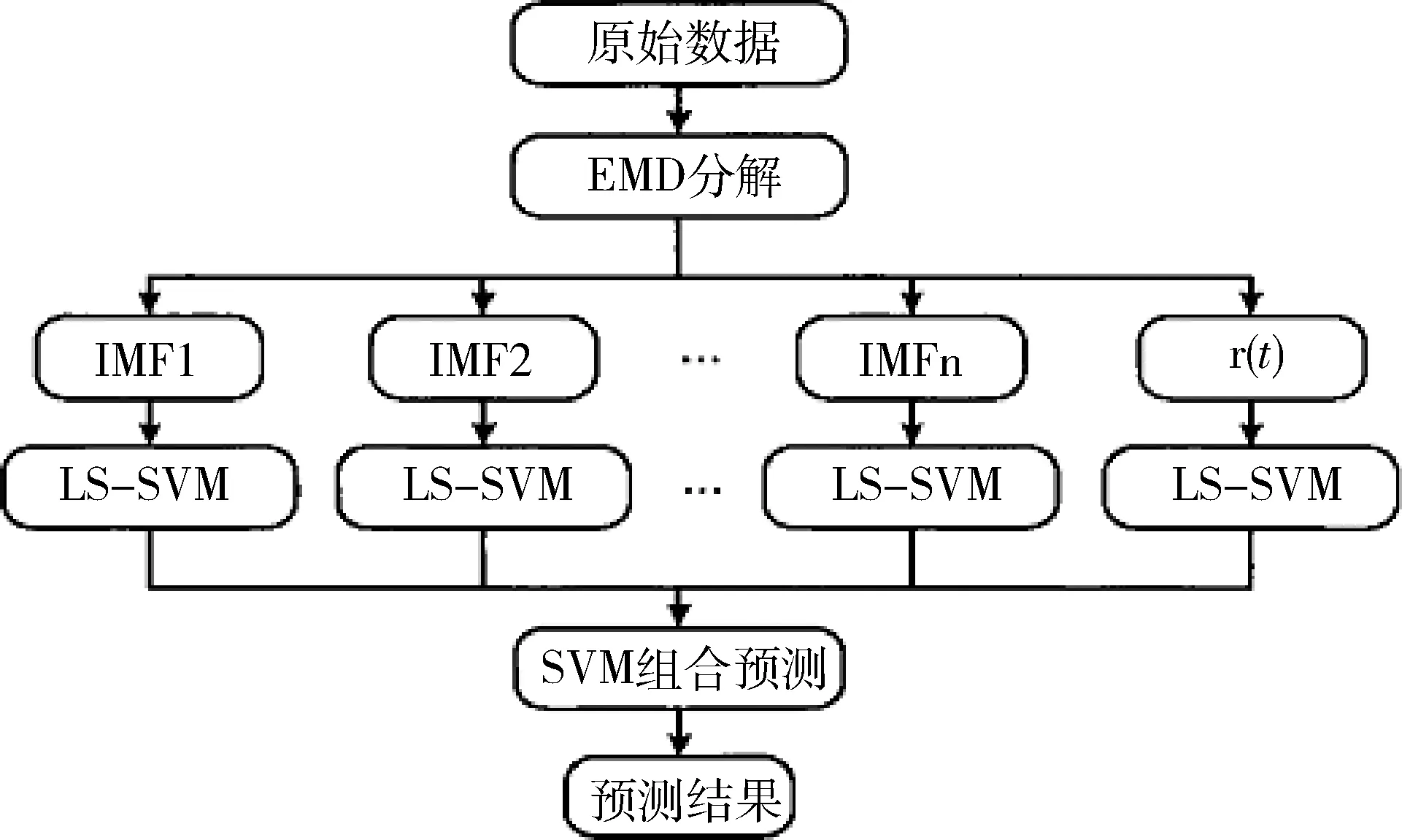
图1 组合预测模型

3 工程实例

北京市锦绣馨园高层建筑，设计为CFG桩和素混凝土夯扩桩组合桩复合地基。2#、4#楼地上24层，地下2层，基础埋深6m，由于建筑与地下车库相连，考虑与地下车库差异沉降，要求最终沉降量不超过40mm。本文对2#楼32#观测点及4#楼22#观测点累计沉降量进行预测研究。仅以4#楼22#观测点为例，对比分析泊松模型预测、改进泊松复合小波模型预测[15]、基于EMD和LS-SVM模型预测的结果与精度。

原始样本数据通过EMD分解，获得2个IMF分量，EMD分解分别如图2～4所示，因此，地基沉降随时间变化共包含了2个IMF分量与余项。对这2个IMF和余项分别进行LS-SVM预测，最终的预测结果如图5所示。

泊松模型预测与改进泊松复合小波模型预测值与实测值见图6、图7。

三种模型的预测值与实测值对比见表1。

泊松模型预测600天的最终沉降量为30.3036mm，绝对误差最大为2.7994mm；改进泊松复合小波模型预测600天的最终沉降量为30.3036mm，绝对误差最大为1.4158mm；基于EMD和LS-SVM模型预测600天的最终沉降量为27.9916mm，绝对误差最为0.4760mm。可见，三种模型预测的最终沉降量均不超过40mm，符合设计要求，且基于EMD和LS-SVM的预测精度最高。

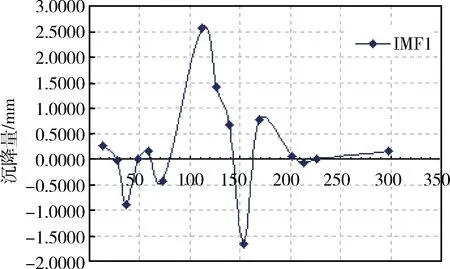
图2 EMD分解IMF1分量

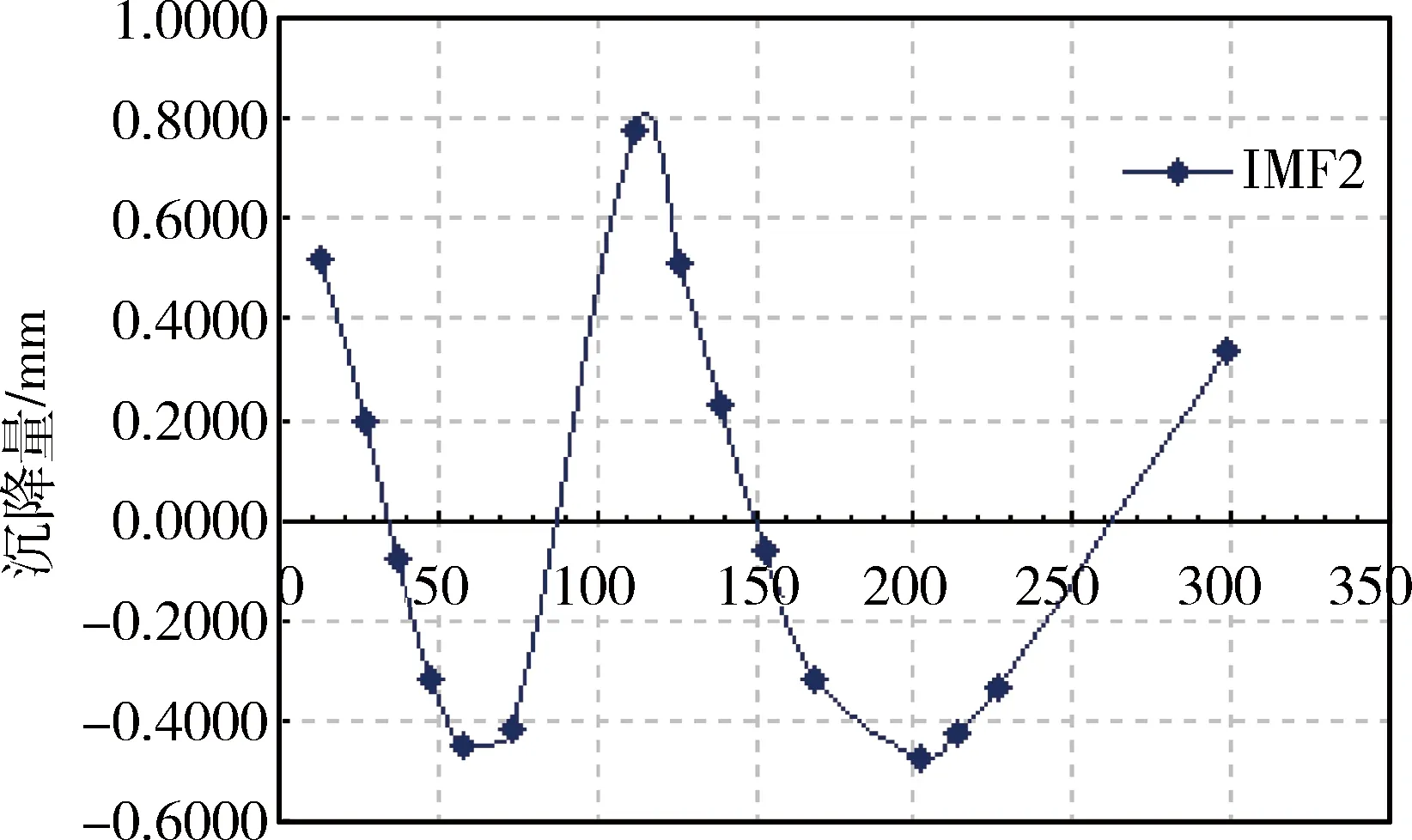
图3 EMD分解IMF2分量

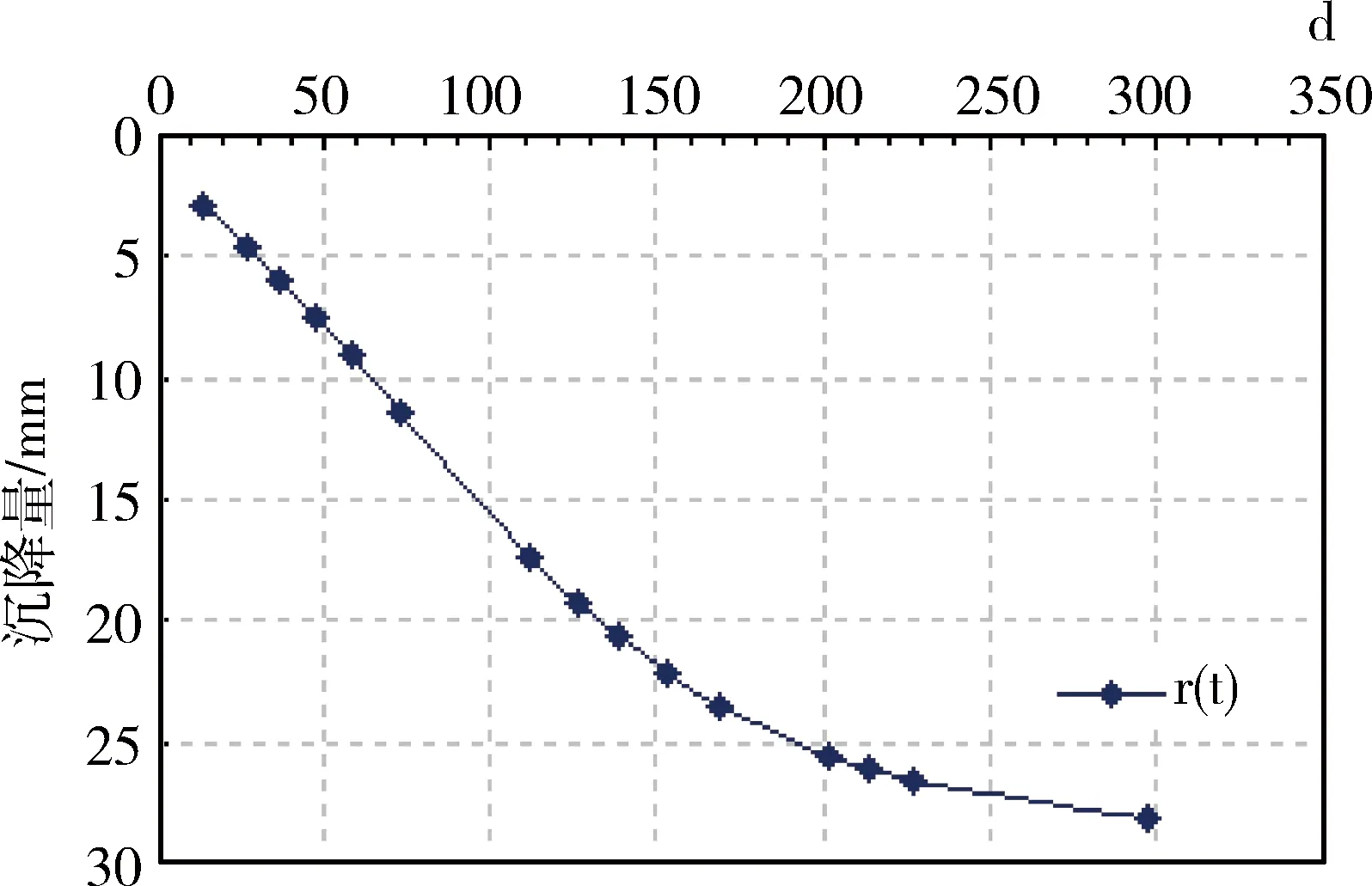
图4 EMD分解余项r(t)

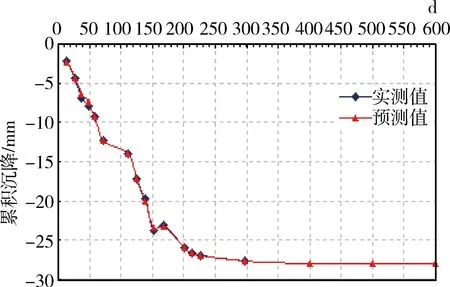
图5 EMD分解和LS-SVM预测值与实测值

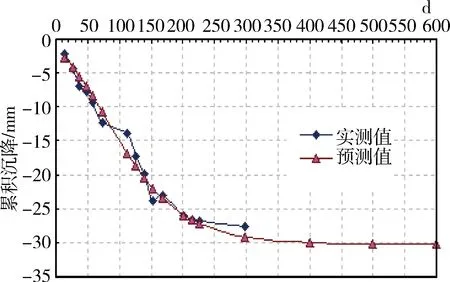
图6 实测值与泊松模型预测值

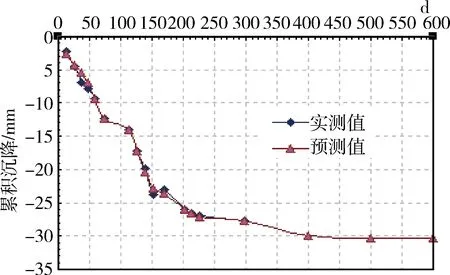
图7 实测值与改进泊松复合小波模型预测值

4 结束语

基于EMD和LS-SVM的复合地基沉降预测得到的地基沉降值与实测值非常相近，表明了该方法具有很强的预测能力。

首先，地基沉降的实际监测数据会受到诸多外界因素影响，通过EMD分解可以有效地对各个干扰信息进行有效地剔除，获得有用信息，从而提高模型本身的预测效果。

其次，地基沉降与外界环境影响因素存在着一定的时间演化特性，环境因素的改变随机特征时间尺度致使地基沉降的时间演化具有明确的特征时间尺度，这是多特征时间模态模型建立的基础。在特征时间的理论框架下，它们可以通过关于特征时间长度的变换的数字处理方法进行辨识。

复合地基沉降增量是随着时间具有确定性演化趋向特性的波动过程，其特征时间模态与实际地基沉降监测数据EMD分解得到的经验模态函数具有极大的关联性。在地基沉降的诸多影响因素中，不同特征时间尺度存在较大的差异，这为通过EMD分解方法获得特征时间模态提供良好的条件。

复合地基沉降预测的相关分析也证实了地基沉降多模态支持向量机预测方法的科学性和可行性，也为深入研究复合地基沉降时间演化规律提供了一条值得探索的理论建模方法。

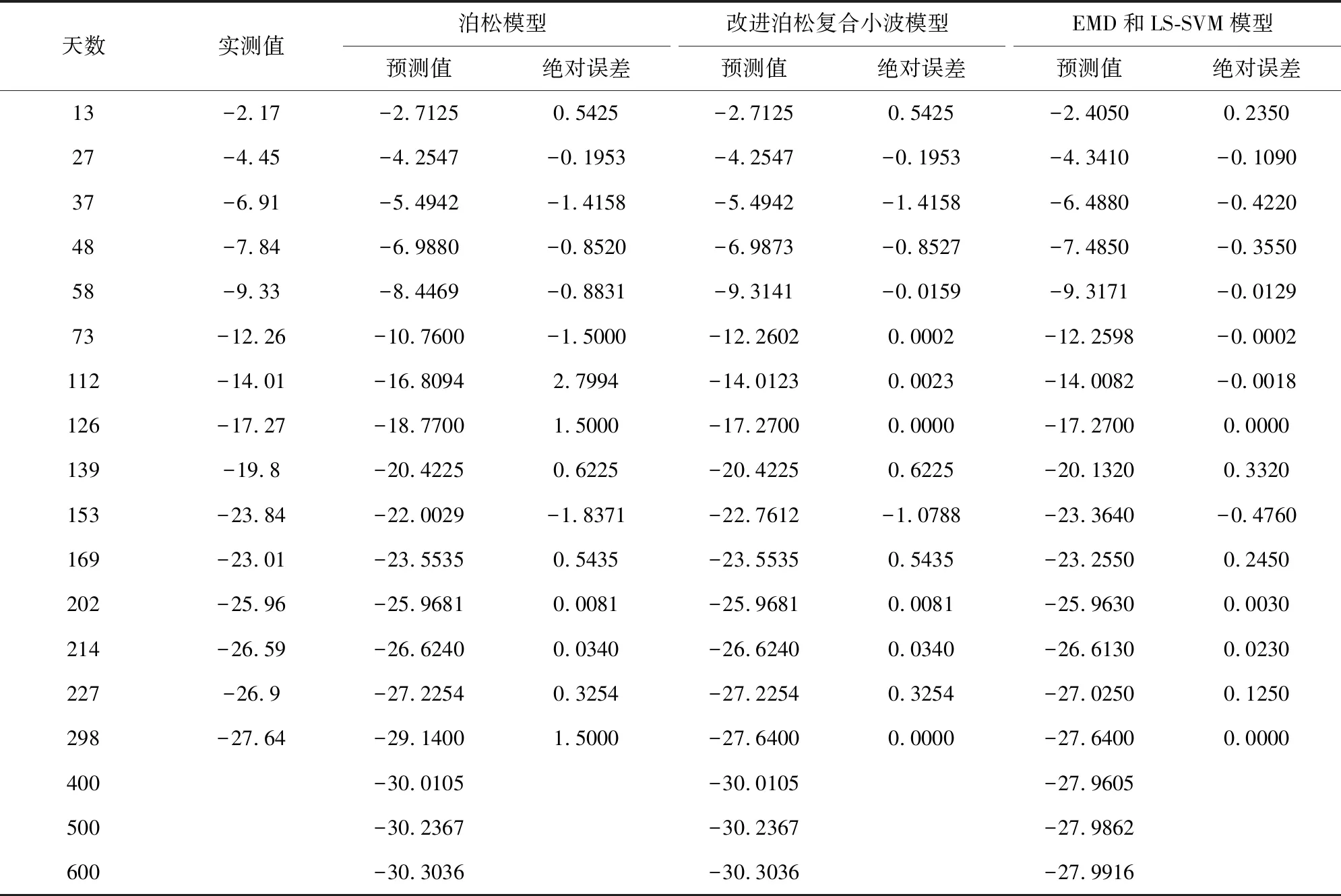
表1 预测值与实测值误差分析/mm

[1] 张丽华，牛庆莲，蔡美峰.复合地基全过程沉降预测的威布尔模型[J].工业建筑，2006,36(10)：54-56.

[2] 宰金珉，梅国雄．泊松曲线的特征及其在沉降预测中的应用[J]．重庆建筑大学学报，2001，23(1)：30-35．

[3] 贾丽杰.双曲线预测复合地基沉降量的合理性研究[J].交通标准化，2006(6)：102-104.

[4] 刘志强，黄张裕.建筑物沉降监测时序分析方法与预测应用[J].勘察科学技术，2006(6)：52-54.

[5] 夏银飞，张季如，夏元友.时间序列在路基填筑期间的应用研究[J].武汉理工大学学报，2005,27(12)：68-71.

[6] 朱睿， 张俊中， 龙洋， 等.时间序列模型在建筑物沉降监测中的应用[J].测绘与空间地理信息，2012,35(2)：212-216.

[7] 王凤池，朱浮声，康玉梅，等.复合地基沉降的模型预测[J].东北大学学报：自然科学版，2004，25(10)：1010-1012.

[8] 张忠苗，辛公锋.刚柔组合桩复合地基沉降的灰色预测[J].工业建筑，2003，33(8)：33-36.

[9] 赵春雨，王连俊，张光宗.基于灰色理论的桩- 筏复合地基沉降预测[J].铁道标准设计，2012(10)：1-3.

[10] 汤梅芳，王炳龙.BP神经网络在悬浮桩复合地基沉降预测中的应用[J].华东交通大学学报，2006,23(2)：15-18.

[11] 李旺林，汤馥郁.BP神经网络在复合地基沉降建模中的应用[J].水利规划与设计，2007(2)：59-61.

[12] 黄亚东，张土乔，俞亭超，等.公路软基沉降预测的支持向量机模型[J].岩土力学，2005,26(12)：1987-1990.

[13] 李德江，花向红，李涛，等.基于支持向量机的建筑物沉降预测模型研究[J].测绘工程，2009,18(3)：29-31.

[14] 林彤，欧阳小良，胡纯清.碎石桩复合地基沉降的组合预测[J].兰州理工大学学报，2010,36(5)：113-116.

[15] 张丽华，蔡美峰.基于改进泊松-复合小波模型的复合地基全过程沉降预测[J].北京科技大学学报，2007,29(9)：869-872.

[16] 朱倩雨， 覃锡忠， 贾振红， 等.基于EMD和粒子群优化的LS-SVM的网络流量预测[J].计算机工程与设计，2013,34(12)：4104-4108.

[17] Zhang X，Lai k K，Wang S Y．A new approach for crude oil price analysis based on empirical mode decomposition[J]．Energy Economics，2008，30(3)：905-918．

[18] WU Haishan，CHANG Xiaoling．Power load forecasting with least squares support vector machines and chaos theory[C]//Proc of Intelligent Control and Automation，2006：4369-4373．