高速列车过隧气压爆波的声学特征与传感器选型

杨志刚，谭晓明，梁习锋，任鑫

(中南大学 交通运输工程学院 轨道交通安全教育部重点实验室，湖南 长沙，410075)

CRH2 高速列车以350 km/h 速度穿越武广高铁某隧道时，隧道出口50 m 位置测试台将监测到沉闷的爆破声；隧道出口20 m 位置的气压爆波幅值大于250 Pa，具有非线性特性。为研究气压爆波的演化规律及控制方法，一般在隧道出口不同位置布置压力传感器或者传声器，观察气压爆波波形变化[1-3]。目前主要应用的传感器有压电膜片式压力传感器和电容膜片式传声器。已有气压爆波的实车试验及模型试验结果表明，不同的传感器选型对测试结果影响较大，但并未引起足够的关注。为此，本文作者从气压爆波的声学时频特征出发，分析气压爆波的近场非线性区及远场线性区，探讨不同传感器应用的合理性，以便为气压爆波的实验研究提供技术支撑。

1 气压爆波时频特征

CRH2 高速列车以250 和350 km/h 速度穿越武广(武汉—广州)高铁某隧道时，传感器监测隧道出口外20 m 位置的气压爆波时间历程以及频谱特征分别如图1 和图2 所示。

由图1 可见：随着列车速度由250 km/h 提高到350 km/h，气压爆波从光滑波形变为近三角波形，幅值急剧增大，并不符合与速度的3 次方关系。从图2可见：气压爆波的主要能量分布在低于20 Hz 的次声波区。表1 所示为对应的频域能量分布统计结果。从表1 可见：当列车速度为250 km/h 时，次声波区能量占总能量的99.85%，气压爆波几乎是纯粹的次声波[4]；当列车速度为350 km/h 时，次声波区能量占总能量的77.03%。

在气压爆波测试传感器的选型方面，应当考虑其低频特征。

表1 气压爆波频谱能量分布统计Table 1 Energy statistics distribution of micro-pressure wave in frequency domain %

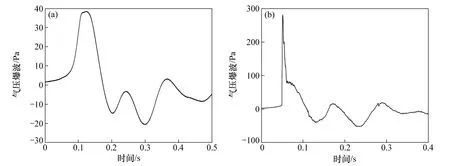
图1 隧道出口外中心线20 m 位置的气压爆波时间历程Fig.1 Time history of micro-pressure wave at 20 m away from tunnel portal

图2 隧道出口外中心线20 m 位置的气压爆波频谱特征Fig.2 Spectrum characteristics of micro-pressure wave at 20 m away from tunnel portal

2 气压爆波的远近场声学特性

采用二维轴对称圆管模型，利用高阶谱差分离散[5-7]的计算气动声学(CAA)仿真技术[8-10]，数值模拟1:20 缩比动模型在不同速度下隧道口外气压爆波随距离的变化，如图3 所示。图3 中，横坐标是以管口直径进行无量纲化的距离，纵坐标是以距离参数归一化的气压爆波幅值。3 条水平的实线代表250，300 和350 km/h 3 种速度级下的气压爆波幅值随距离的理想线性衰减情况。

由图3 可见：在近隧道口区域，气压爆波幅值随距离并未按照线性规律衰减；在远场，则接近线性规律衰减[11-12]；列车进入隧道的速度越大，隧道出口气压爆波幅值的近场传播非线性特征越明显。这是由于随着列车速度的提高，隧道口的气压爆波源增强，对应的气动噪声源区向外扩展。对图3 所示的结果以误差5%来计算，管口外约2 个管口直径范围内为非线性声传播的声源区。

在这个近隧道口的气动噪声源区，存在局部气流的质量运动，这对传感器的选型有一定影响。在这个区域，电容式的传声器并不能准确地测得气压爆波波形。

图3 隧道出口外气压爆波传播规律Fig.3 Propagation of micro-pressure wave at tunnel exit

3 传感器的选型

这里讨论的传感器主要有3 种：压电膜片式的差压传感器、电容膜片式的B&K 4189 自由场传声器和B&K 4193 次声波传声器。

3.1 传感器的频率响应范围对测试结果的影响

下面对这3 种传感器的气压爆波测试结果进行对比，以探讨合理的选型方案。表2 所示为这3 种传感器的频率响应范围。

表3 所示为高速列车以不同速度通过在武广某隧道时、使用这3 种传感器在隧道口外20 m 位置测得的气压爆波幅值。

表2 测试传感器特性比较Table 2 Performance comparison of test sensors

表3 武广某隧道口外20 m 位置气压爆波幅值比较Table 3 Amplitude comparison of micro-pressure wave at 20 m away from Wuhan—Guangzhou tunnel portal Pa

由表3 可见：差压传感器和B&K 4 193 次声波传声器的频响均能覆盖整个次声波区，其测试结果合理且比较接近，B&K4189 自由场传声器由于6.3 Hz 低频截止限制导致较大的误差(表3 中最大相对误差超过50%)；在200～250 km/h 下，由于其气压爆波能量99%以上均在次声波区，采用B&K4189 自由场传声器会导致更大的误差，因此，相对而言，采用差压传感器和B&K4193 次声波传声器比较适合。

需注意的是：在列车速度为340 km/h 时，二者的结果出现了一定的偏差(相对误差约5%)。这是由于在这种情况下，气压爆波的能量分布比低速情况下占据了更宽的频率范围(20 Hz～1 kHz 区间的能量分布不容忽视)。差压传感器的频响范围低于1 kHz，在气压爆波能量分布的高频边缘区域会导致测试误差，从而影响测试精度。因此，在高速、大幅值(超过250 Pa)的特殊情况下，应选用具有更高响应频率范围的压力传感器。

3.2 远、近场测试时对传感器类型的要求

实验发现，选用差压传感器或B&K4193 次声波传声器的气压爆波测试结果尽管幅值很接近，但波形往往并不一致。

图4(a)所示为隧道口外10 m位置测得的气压爆波波形，图4(b)所示为隧道口外20 m 位置测得的气压爆波波形；点划线为差压传感器的测试结果，实线为B&K4193 次声波传声器的测试结果。由图4 可见：这2 种传感器的测试结果在气压爆波的上升沿基本一致，在下降沿后有很大差别。

图4 隧道出口外10 m 和20 m 位置的气压爆波波形Fig.4 Waveforms of micro-pressure wave at 10 m and 20 m away from tunnel portal

考虑到第2 节的气动噪声源区问题，10 m 和20 m位置均在管口外2 倍管口直径区域内，属于气动噪声源区。在该区域，存在由于空间上的气体质量交换导致的压力变化(包括了压力的近稳态变化)。差压传感器能够捕捉流场的所有变化信息，传声器仅仅监测气压爆波传递的声振动能量，因而，在近场声源区，差压传感器能够更加准确地监测气压爆波。

在4～5 倍管口直径外的远场，选用这2 种传感器进行测量，将得到较一致的结果。

4 结论

(1) 气压爆波的大部分能量分布在次声波区，必须选用能够覆盖整个次声波区频率范围的传感器进行气压爆波测试研究，B&K4189 自由场传声器不适用。

(2) 当列车速度较低时(250 km/h)，气压爆波99%以上能量分布在次声波区，可以看作纯粹的次声波，一般采用次声波传感器或者稳态压力传感器均可得到准确结果。

(3) 随着列车速度的提高，气压爆波的部分能量分布向较高频率转移，必须考虑传感器1 kHz 以下的频响特性。对高速的特殊情况(气压爆波幅值超过250 Pa)，应选用具有更高响应频率范围的动态压力传感器。

(4) 隧道口存在气动噪声源区，约在2 倍管口直径范围内。在近场声源区，差压传感器相对传声器能够更加准确地反映气压爆波的实际情况；在远场，选用这2 种传感器进行测量，可得到较一致的结果。

(5) 目前普遍采用气压爆波幅值作为评判气压爆波大小的标准量，并未对气压爆波的频谱范围进行规范。由于个体研究采用的测试系统不同，在实际操作中，可能导致较大误差，建议在将来气压爆波的行业标准制定时，规范其频谱特性，进而规范其测试技术。

[1] Raghunathan R S, Kimb H D, Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences,2002, 38: 469-514.

[2] 刘堂红, 田红旗, 金学松. 隧道空气动力学实车试验研究[J].空气动力学学报, 2008, 26(1): 42-46.LIU Tanghong, TIAN Hongqi, JIN Xuesong. Experimental study of full-scale train on aerodynamics in tunnel[J]. Acta Aerodynamica Sinica, 2008, 26(1): 42-46.

[3] 王英学, 高波, 郑长青, 等. 高速列车进入隧道产生的微气压波实验研究[J]. 实验流体力学, 2006, 20(1): 5-8.WANG Yingxue, GAO Bo, ZHENG Changqing, et al.Micro-compression wave model experiment on the high-speed train entering tunnel[J]. Journal of Experiments Fluid Mechanics,2006, 20(1): 5-8.

[4] Yoon T S, Lee S, Hwang J H, et al. Prediction and validation on the sonic boom by a high-speed train entering a runnel[J].Journal of Sound and Vibration, 2001, 247(2): 195-211.

[5] Liu Y, Vinokur M, Wang Z J. Spectral difference method for unstructured grids I: Basic formulation[J]. Journal of Computational Physics, 2006, 216: 780-801.

[6] Wang Z J, Liu Y, May G, et al. Spectral difference method for unstructured grids II: Extension to the Euler equations[J].Journal of Scientific Computing, 2007, 32(1): 45-71.

[7] GAO Junhui, YANG Zhigang, LI Xiaodong. An optimized spectral difference scheme for CAA problems[J]. Journal of Computational Physics, 2012, 231: 4848-4866.

[8] Hu F Q, Li X D, Lin D K. Absorbing boundary conditions for nonlinear Euler and Navier-Stokes equations based on the perfectly matched layer technique[J]. Journal of Computational Physics, 2008, 227: 4398-4424.

[9] Hu F Q. Development of PML absorbing boundary conditions for computational aeroacoustics:A progress review[J].Computers & Fluids, 2008, 37(4): 336-348.

[10] LIU Li, LI Xiaodong, Hu F Q. Nonuniform time-step Runge-Kutta discontinuous Galerkin method for computational aeroacoustics[J]. Journal of Computational Physics, 2010, 229:6874-6897.

[11] Howe M S, Iida M, Fukuda T, et al. Theoretical and experimental investigation of the compression wave generated by a train entering a tunnel with a flared portal[J]. Journal of Fluid Mechanics, 2000, 425: 111-132.

[12] Aoki T, Vardy A E, Brown J M B. Passive alleviation of micro-pressure waves from tunnel portals[J]. Journal of Sound and Vibration, 1999, 220(5): 921-940.