基于改进有限容积法的数群平衡方程数值方法研究

赵腾磊，刘志强，徐爱祥，何娜萍

(中南大学 能源科学与工程学院，湖南 长沙，410083)

数群平衡模型(population balance model, PBM)主要用于研究离散系统中颗粒粒度分布函数的时间演变过程[1]。它用数群平衡方程(population balance equation,PBE)描述由于颗粒增长、团聚、破碎等作用引起颗粒粒度分布随时间的变化。数群平衡模型首先是被用在化学工程学科中[2-3]。随着数值计算和高速计算机的发展，数群平衡模型被应用在多个科学与工程学学科中[4-6]。实际运用过程中，数群平衡方程精确的数值模拟需要一个合适的数值计算方法。许多该领域的学者已经发展了多个数值计算方法解数群平衡方程，如Lee 等[7]的Monte Carlo 法，Hill 等[8]的有限差分法，Daniele 等[9]的正交矩方法，Everson 等[10]的有限元法。经过研究发现，运用这些方法所得数值解具有扩散性或者不稳定性[11]。现在运用最多的数值方法是改进有限容积法，即特征法(method of characteristics, MOC)和有限容积法(finite volume schemes, FVS)结合的数值方法，这种数值计算方法是根据方程的数学特征进行数学变换，用有限容积法对变换后的方程求解。Qamar等[4]对改进有限容积法进行了描述，并分别运用改进有限容积法和有限容积法对数群平衡方程进行求解，把用2 种数值方法计算结果分别和分析解对比，分析了2 种数值方法的效果。数学变换是根据生长项和团聚项的数学特征对两项进行不同的变换，Qamar 等[4]只对几种动力学事件下粒子的分布进行求解，并没有对单独考虑1 种变换以及同时考虑2 种变换的情况进行计算，分析每一种变换对计算颗粒粒度分布的影响。为此，本文作者采用非均匀对数网格对计算区域进行离散，用有限容积法解数学变换后的数群平衡方程，分别求解纯生长事件、纯团聚事件和同时考虑生长和团聚作用下的颗粒粒度分布，把数值解和分析解进行对比，分析数值求解方法的有效性；用所得数值结果与Qamar等[4]和Kumar 等[12]直接用有限容积法解数群平衡方程计算所得结果进行比较，分析每一种变换对颗粒粒度分布的影响以及本文所用数值方法的优点。

1 数群平衡模型

离散系统的数群平衡方程是描述体积分布函数的动态变化。这里主要是用常用的数学方法对一维数群平衡方程进行变换。Perry 等[13]给出了离散系统的一维数群平衡方程：

式中：f(t,x)为单位体积载流体中分散相的数量密度；G(t,x) 为生长速率，表示t 时刻单位时间体积为x 的颗粒粒度增长的大小[14]；Aagg(t,x) 为团聚项；Bbreak(t,x)为破碎项；S(t,x) 为成核项。本文没有涉及到成核项的变换，破碎项和团聚项的变换是相同的，为了便于计算与对比，只考虑生长和团聚作用下颗粒粒度分布。故方程(1)变换为：

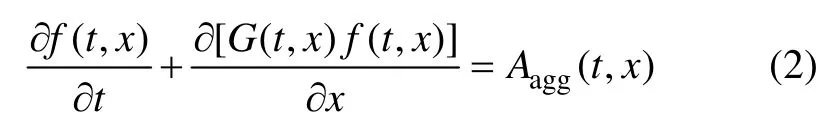
初始分布为：

团聚项定义为：

方程(3)右边第1 项表示体积为y 和x-y 的颗粒聚合为体积为x 的颗粒数量；第2 项表示体积为x 的颗粒和其他颗粒团聚而减少的数量；β(t,x,y)表示颗粒的团聚率，即t 时刻体积为x 与y 的颗粒碰撞后发生团聚事件的速率[1]。

生长作用主要影响颗粒体积大小，对颗粒总数量没有影响；团聚作用主要影响颗粒数量，颗粒总体积不变。理论上颗粒会发生生长和团聚直到体积无穷大，但是实际颗粒会受到其他作用影响，体积不会无限增长。体积比较大的颗粒数量较少，在方程的计算过程中会用截断误差对方程进行处理。假如直接把有限容积法应用到数群平衡方程中，需要把团聚项作为源项处理。当团聚作用大于生长作用时，可能导致截断误差较大，颗粒质量损失较大，方程不守恒性增大，得到不真实的解。为了解决这个问题，把团聚项作为网格通量处理，即把数量守恒形式的数群平衡方程变换为质量守恒形式的方程。

把方程(2)和(3)左右两边同时乘以x：

令：xAagg(t , x)=-∂Fagg(t , x )/∂x ，根据方程(3)得出：

2 求解方法

2.1 区域离散

为了运用数值方法对方程求解，首先要对计算区域进行离散。区域离散包括建立均匀网格和非均匀网格。当颗粒粒度范围较小时，非均匀几何网格更加合理。本文所取计算范围较小，故对计算区域建立非均匀几何网格。一维几何网格为：

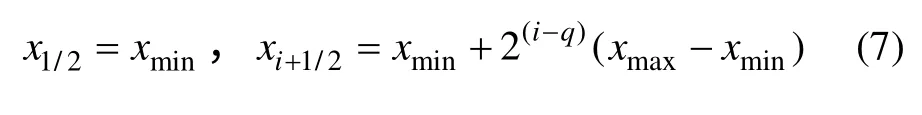
式中：q 表示在小颗粒粒度范围内网格加密程度。

2.2 数值方法

当生长速率较大时，直接用有限容积法解数群平衡方程质量损失较大，具体表现为方程的截断误差较大。在数群平衡方程中生长项为方程的对流项，为了减小方程生长项所引起的误差，主要针对方程的对流项进行变换。根据生长速率的数学特征对原始数群平衡方程进行数学变换，用有限容积法对变换后的方程进行计算。根据线性标量守恒定律，沿着颗粒粒度分布曲线移动方向有唯一的特征曲线。假如解沿着传播路径的方向移动，利用生长速率的特征使方程(6)的对流项消失。

用以下方程替代生长速率：dx/dt=G(t,x)

将式(6)在控制体积Ωi=[xi-1/2(t)，xi+1/2(t)]上积分：

Filbet 等[15]给出了团聚项的离散形式：

其中：αi,k是当xi+1/2- xk∈Ωαi,k-1(t )时，网格节点的数字符号。

初始条件：

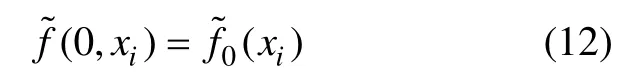
在计算区域以外的部分数量密度为零，即方程的边界上的数量密度设置为零。也就是说，在设定计算区域以外没有更大和更小的颗粒。

3 数值结果与讨论

用以上数群平衡方程数值计算方法计算纯生长、纯团聚、生长和团聚同时作用下颗粒粒度分布。为了说明改进有限容积法计算数群平衡方程的有效性，把数值计算结果和分析结果进行对比。本文还给出了Qamar 等[4]和Kumar 等[12]直接用有限容积法解数群平衡方程所得结果，通过2 种数值方法计算结果与分析解的对比，分析每一种变换对颗粒粒度分布的影响以及本文所用数值方法的优点。本文不针对具体的物理模型计算，只考虑数值计算方法对数群平衡模型的计算效果。本文用Matlab 自编程对数群平衡方程的离散公式求解。

3.1 生长

对比在常数生长(constant growth)和线性生长(linear growth)条件下计算数群平衡方程的数值解和分析解。

常数生长速率G(t,x)=G0，初始分布为：

式中：N0和x0分别代表初始时刻颗粒总数量和颗粒平均体积，分析解为

令G0=1，N0=5，x0=0.01，q=3，取60 个网格节点。

图1 所示为2 种数值计算方法计算常数生长条件下颗粒粒度分布数值结果和分析解的对比。图1(a)所示为用改进有限容积法计算的数值解和分析解的对比，从图1(a)可知数值解和分析解基本一致。图1(b)[11]所示为用有限容积法计算的数值结果和分析解的对比，从图1(b)可知数值解和分析解基本一致，但是在小颗粒处出现了解的失真。由图1 可知：小颗粒生长速度较快，而大颗粒粒度几乎不变。

图1 颗粒常数生长作用下的粒径分布Fig.1 Ice crystal size distributions for constant growth process

线性生长速率G(t,x)=G0x，初始分布为方程(13)。在数值计算中，令G0=1，N0=5，x0=0.01，q=3，取60个网格点。Kumar 等[16]给出分析解为：

图2 所示为2 种数值计算方法计算线性生长条件下颗粒粒度分布数值解和分析解的对比。图2(a)所示为用改进有限容积法计算的数值解和分析解的对比，从图2(a)可知数值解和分析解一致性较好，随着时间增加计算误差增大，但数值解没有出现不真实、不稳定等现象。图2(b)[11]所示为用有限容积法计算的数值结果和分析解的对比，从图2(b)可知数值解和分析解基本一致，但在小颗粒处出现了解的失真。由图2 可知：线性增长使颗粒粒度不断生长的同时使颗粒粒度分布概率改变，小颗粒的概率不断减小，大颗粒概率增加，总的颗粒数目没有改变。

图2 颗粒线性生长作用下的粒径分布Fig.2 Ice crystal size distributions for linear growth process

图1 和图2 所示为在纯生长作用下，颗粒粒度不断长大，而颗粒数量几乎不变。从图1 和图2 可知：粒度较小的颗粒生长速率较大，使得质量损失对小颗粒粒度的分布影响较大，故小颗粒粒度分布的数值解出现失真现象。数群平衡方程是一个非标准输运控制方程，对流项中增加了生长速率的影响，直接用有限容积法对方程进行计算，计算所得的数值结果会出现失真现象。与有限容积法对比，改进有限容积法使得方程中对流项消失，减少了生长速率对方程计算结果的影响。从以上2 种计算结果可知对流项消失使得方程的解没有出现失真。

3.2 团聚

对比用 2 种数值方法计算常数团聚(constant aggregation)和合团聚(sum aggregation)问题所得数值解和分析解。

常数团聚速率β(t,x,y)=β0，初始分布为方程(13)，令β0=1，N0=5，x0=0.01，取91 个网格节点。Kumar等[12]给出常数团聚作用下数群平衡方程的分析解为：

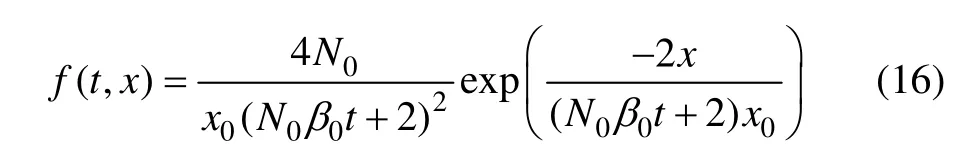
由图3(a)和图3(b)[12]对比可知：用2 种数值计算方法计算数群平衡方程所得数值解和分析解误差很小，在±5%以内。在常数团聚作用下用2 种数值方法计算的数值解没有出现不稳定、扩散以及失真的现象。随着时间不断增加，小颗粒数量不断减少，大颗粒数量不断增加，颗粒总的体积几乎没有变化。

图3 颗粒常数团聚作用下的粒径分布Fig.3 Ice crystal size distributions for constant aggregation process

合团聚速率β(t,x,y)=β0(x+x′)，初始分布为方程(13)。在数值计算中，令β0=1，N0=5，x0=0.01，取91个网格节点。Kumar 等[12]给出分析解为

其中：τ=1-exp(-Ta)；I1是一阶贝塞尔函数。

由图4(a)和图4(b)[12]对比可知：用2 种数值计算方法计算数群平衡方程所得数值解和分析解基本一致，与分析解的误差都很小。在线性团聚作用下用两种数值方法计算的数值解同样没有出现不稳定、扩散或者失真等现象。随着时间不断增加，小颗粒数量不断减少，大颗粒数量不断增加，小颗粒减少速率比大颗粒增加速率小，颗粒总的体积几乎没有变化。

图4 颗粒合团聚作用下的粒径分布Fig.4 Ice crystal size distributions for sum aggregation process

通过以上2 种团聚事件作用下计算的颗粒粒度分布数值解和分析解的对比，可知在纯团聚作用下，2种方法计算结果误差不大。团聚作用只对颗粒数目有影响，对颗粒总的体积几乎没有影响，也就是说质量是守恒的，质量损失较小，故用2 种方法计算的数值解没有出现失真。

3.3 生长和团聚

对比用2 种数值方法计算同时考虑生长和团聚的数群平衡方程的数值解和分析解。本文考虑不同生长速率和团聚速率结合的3 种颗粒粒度演化情况，3 种情况初始分布都为方程(13)。3 种不同的动力学过程如表1 所示[12,16-17]。

表1 生长和团聚作用下不同动力学参数组合的动力学过程Table 1 Kinetic processes of different kinetic parameters under growth and breakage

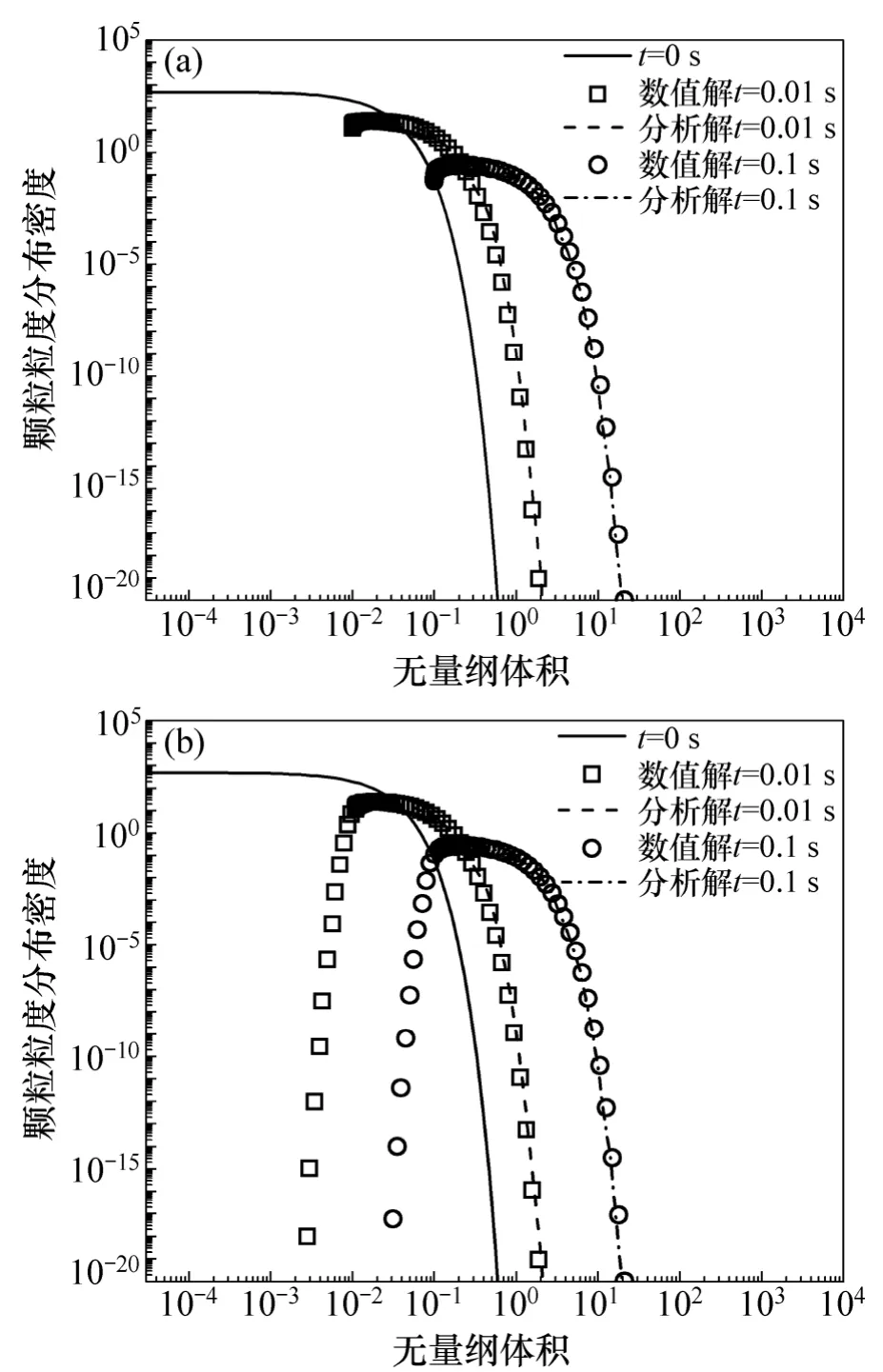
图5 颗粒常数增长和常数团聚作用下的粒径分布Fig.5 Ice crystal size distributions for constant growth and constant aggregation process

图5 所示为表1 中第1 种情况的数值计算结果与分析解的对比。取G0=1，β0=100，N0=5，x0=0.01，q=4，取91 个网格节点。图5(a)和图5(b)[11]所示为用2 种求解方法计算的数值结果和分析解基本一致。甚至要求误差非常小的情况下，这2 种方法所得的数值解也是非常有效的。然而有限容积法计算结果在左边界出现失真现象，在其他区域与分析解是一致的。

图5(a)所示在左边界数值解和分析解有一些差别，但是不明显。这是由于这个区间范围的分析解有误差。Kumar 等[15]指出在生长速率和团聚速率相等时，常数增长和常数团聚的分析解只是在大颗粒处有效；当团聚作用明显时，分析解的有效范围增大；当生长速率明显时，分析解会产生一定的误差。

图6 所示为表1 中第2 种情况的数值计算结果。取G0=1，β0=10，N0=5，x0=0.01，q=4，取91 个网格节点。图6(a)和图6(b)[11]所示为用2 种求解方法计算的数值结果和分析解基本一致。有限容积法计算结果在左边界同样出现失真现象，在其他区域与分析解是一致的。这种情况下整个计算区域的颗粒团聚作用比较明显，分析解在整个计算区域都有效，所以图6(a)中数值解没有和分析解产生较大误差。

图7 所示为表1 中第3 种情况的数值计算结果。取G0=1，β0=1，N0=5，x0=0.01，q=4，取91 个网格节点。图7(a)和图7(b)[11]表示用2 种求解方法计算的数值结果和分析解基本一致。有限容积法计算结果在左边界同样出现失真现象，在其他区域与分析解同样是一致的。这种情况同样由于在整个计算域上团聚作用比较明显，所以图7(a)中的分析解比较有效，没有与数值解产生较大误差。

图6 颗粒线性增长和常数团聚作用下的粒径分布Fig.6 Ice crystal size distributions for linear growth and constant aggregation process

图7 颗粒常数增长和合团聚作用下的粒径分布Fig.7 Ice crystal size distributions for linear growth and sum aggregation process

直接运用有限容积法对数群平衡方程进行计算时，只能保证颗粒数量守恒，不能保证颗粒质量守恒。假如同时考虑生长和团聚作用对颗粒粒度的分布，当团聚作用较小时，颗粒质量损失较小，方程数值解不会出现失真；当团聚作用比生长作用明显时，颗粒质量损失较大，方程质量不守恒性也会增大，方程数值解会出现失真。表1[17]中3 种情况都是团聚速率比生长速率大的情况，而且团聚速率第1 种情况最大，第3 种情况最小。根据3 种情况计算结果可知：直接运用有限容积法解数群平衡方程会出现解的扩散，而且团聚速率越大失真现象越明显；而用经过数学变换后的有限容积法计算减小了颗粒质量损失，使方程不守恒性减小，方程数值解没有出现失真。

4 结论

(1) 纯生长条件下求解数群平衡方程，与有限容积法相比，本文所用求解方法消除了方程中对流项的影响，减小了方程解的失真。

(2) 团聚作用只是影响颗粒数量分布，几乎没有质量损失。纯团聚条件下求解数群平衡方程，两种数值求解方法所得数值结果都和分析解基本一致。

(3) 有限容积法只可以保证颗粒分布数量的守恒，不能保证颗粒质量守恒。在生长和团聚同时作用条件下对数群平衡方程求解，当团聚作用比较大时，运用有限容积法所得数值解会出现失真；而且当团聚作用越大时，数值解的失真现象越明显。本文对数群平衡方程进行数学变换，即使方程团聚项作为网格通量处理，使得方程质量守恒，数值解的失真现象消失。

[1] 赵海波, 郑楚光. 离散系统动力学演变过程的颗粒群平衡模拟[M]. 北京: 科学出版社, 2008: 13-18.ZHAO Haibo, ZHENG Chuguang. Population balance modeling for the process of the dynamic evolution in dispersed systems[M]. Beijing: Science Press, 2008: 13-18.

[2] Hulbert H M, Katz S. Some problems in particle technology[J].Chemical Engineering Science, 1995, 19: 555-574.

[3] Randolph A, Larson M A. Theory of particulate processes[M].2nd ed. San Diego: Academic Press, 1988: 7-19.

[4] Qamar S, Warnecke G, Elsner M P. On the solution of population balances for nucleation, growth, aggregation and breakage processes[J]. Chemical Engineering Science, 2009, 64:2088-2095.

[5] Kauffeld M, Wang M, Goldstein V, et al. Ice slurry applications[J]. International Journal of Refrigeration, 2010,33(8): 1491-1505.

[6] Bellas I, Tassou S A. Present and future applications of ice slurries[J]. International Journal of Refrigeration, 2005, 28(1):115-121.

[7] Lee K, Matsoukas T. Simultaneous coagulation and breakage using constant—N Monte Carlo[J]. Powder Technology, 2000,110: 82-89.

[8] Hill P J, Ng K M. New discretization procedure for the breakage equation[J]. AIChE Journal, 1995, 41: 1204-1216.

[9] Daniele L M, Dennis R V, Rodney O F. Quadrature method of moments for aggregation-breakage processes[J]. Colloid Interface Science, 2003, 258: 322-334.

[10] Everson R C, Eyre D, Campbell Q P. Spline method for solving continuous batch grinding and similarity equations[J].Computers & Chemical Engineering, 1997, 21: 1433-1440.

[11] Qamar S, Warnecke G. Numerical solution of population balance equations for nucleation, growth and aggregation processes[J].Computers & Chemical Engineering, 2007, 31: 1576-1589.

[12] Kumar J, WarnecKe G, Peglow M, et al. Comparison of numerical methods for solving population balance equations incorporating aggregation and breakage[J]. Power Technology,2009, 189: 218-299.

[13] Perry R H, Green D W. Perry’s chemical engineers’handbook[M]. 7th ed. New York: McGraw-Hill, 1997: 107-116.

[14] Ramkrishna D. Population balances theory and applications to particulate systems in engineering[M]. San Diego: Academic Press, 2000: 47-59.

[15] Filbet F, Laurençot P. Numerical simulation of the Smoluchowski coagulation equation[J]. SIAM Journal Scientific Computing, 2004, 25(6): 2004-2048.

[16] Kumar S, Ramkrishna D. On the solution of population balance equations by discretization-III. Nucleation, growth and aggregation of particles[J]. Chemical Engineering Science, 1997,52: 4659-4679.

[17] Ramabhadran T E, Peterson T W, Seinfeld J H. Dynamics of aerosol coagulation and condensation[J]. AIChE Journal, 1976,22: 840-851.