结构流充填料浆管道输送阻力特性

吴爱祥，刘晓辉，王洪江，王贻明，焦华喆，刘斯忠

(北京科技大学 土木与环境工程学院 金属矿山高效开采与安全教育部重点实验室，北京，100083)

近年来，随着矿山环境污染及安全生产等问题的日益显著，尾矿充填采矿技术逐渐成为地下开采的主导工艺，为选厂尾矿的处置提供了新的途径，同时有效控制了地压活动，保障了井下回采安全。膏体充填是目前矿山充填技术的发展方向，其具有尾矿利用率大、含水率低、充填强度高等优点[1-2]。但同时，膏体充填料浆中含有大量细粒尾矿，固含较高，且混合有絮凝剂等化学药剂[3]，由此导致其流动特性复杂，对其管道输送阻力特性的研究一直是众多学者关注的重点。研究表明：在膏体料浆中，固体颗粒在表面物理化学作用下将产生具有一定强度的絮网结构，由此导致其在管道中呈整体流动，即称之为结构流体[4-6]。对于结构流管道输送阻力特性的研究，一般从流变学入手，如翟勇刚等[7]和王劼等[8]在对会泽膏体充填料浆的研究中，将其视作为宾汉姆流体，并基于白金汉姆公式对管道阻力进行了计算。张宗生[9]及王五松等[10]对金川膏体进行流变测试，发现H-B 流变模型具有更好的适用性，并推导了其相应的管阻计算模型。此外，Hallbom 等[11]提出了一种膏体流变关系的通用模型(yield plastic model，Y-P 模型)，并利用该模型对管输阻力进行了分析。上述研究均是将浆体流变关系视作为与剪切作用无关的函数，进而分析其管阻特性的变化。事实上，对于结构流体而言，不同的剪切作用对其内部结构的破坏程度各异，必然导致流变关系及管阻特性的改变。因此，本文作者首先基于结构动力学理论对剪切作用下浆体絮网结构的动态变化过程进行了描述，同时结合宾汉姆流体模型建立了考虑浆体内部结构变化的流变关系模型，最终通过水力学推导探讨了结构流管阻特性的变化规律，为管道输送参数的优化提供了新的思路。

1 剪切过程中絮网结构动态变化

膏体充填料浆中包含有大量的细粒尾矿，单位体积内固体颗粒的表面积较大，由此导致颗粒间的相互作用较强。细颗粒在水中吸附异性离子，形成双电层的带电颗粒，在表面电场的作用下互相吸引，进而逐渐搭接形成絮团，这种由单个颗粒结合成集合体的过程称为絮凝作用。随着浆体浓度的提高，颗粒絮凝不断发展，当絮团数达到一定数量之后，絮团之间开始发生连接，形成一种松散的网状结构，称之为絮网结构[12]。絮网结构的存在，使颗粒本身的特性消失，取而代之的是絮网整体特性的呈现[13]。在管内流动过程中，浆体絮网结构受到剪切作用，其可由剪切速率γ及作用时间t 来进行衡量，根据水力学理论[14]，剪切速率与流速v 及管径D 相关：

在剪切过程中，浆体絮网结构一方面在外力作用下拉断、破坏；同时，由于颗粒间的相互作用，结构又不断搭接，修复。当破坏速率与修复速率相等时，结构最终达到动态平衡。Jarny 等[15-16]提出以结构系数S 来对此进行描述，其假设絮网结构的变化可由破坏和修复2 个可逆过程组成，有下式成立：

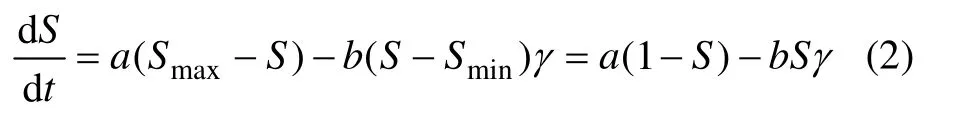
式中：a 和b 分别为絮网结构的恢复系数及破坏系数，均为正值，对于相同浆体，其值恒定；S 为结构系数；Smax为絮网结构完全发育时的结构系数，可假定其值为1；Smin为结构完全破坏时的结构系数，假定为0；γ 为剪切速率，s-1[17]。

由式(2)可知，S 越大浆体结构越发育，反之亦然，当dS/dt =0 时，则为达到动态平衡时的结构系数Se，如式(3)所示：

式中：β=b/a。

由式(3)可知：在浆体其他条件不变的情况下，改变剪切作用强度，将导致浆体平衡结构系数的变化，剪切作用越强(即γ 越大)，则浆体结构的破坏越充分，Se相应越小。对式(1)两边积分，则可得到结构系数S随时间t 及剪切速率γ˙的变化规律，如下式所示：

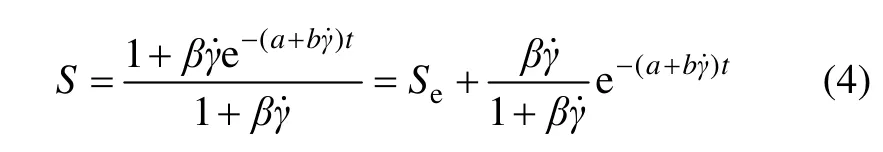
分析可知：在某剪切速率作用下，浆体最终将达到平衡结构系数Se，而不同的剪切作用强度，对应有不同的Se。

2 结构流管道阻力特性

流变性质是研究结构流体管道阻力特性的根本出发点，在以往的研究中，一般将充填料浆视作为宾汉流体，如下式所示：

式中：τy及μp分别为屈服应力及塑性黏度，同时认为，该值是与时间t 及剪切速率γ 无关的参量，并由此推导了其管道阻力的理论计算公式，如式(6)所示，在输送条件(管径、浆体)确定的条件下，管阻损失im随流速v 呈线性增加。

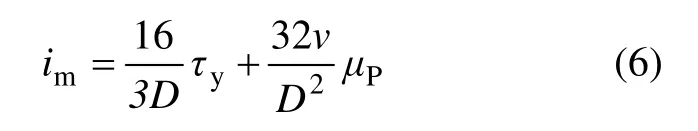
式中：im为管输阻力损失，Pa/m；τy为浆体屈服应力，Pa；μP为浆体塑性黏度，Pa/s；v 为输送流速，m/s；D 为管径，m。

由前述分析表明，对于结构流体，由于其内部絮网结构的存在，剪切作用条件不同，将导致相应流变参数(τy及μp)的变化。韩文亮等[13,18-19]提出将屈服应力τy及塑性黏度μp视为与絮网结构系数S 相关的变量，有：

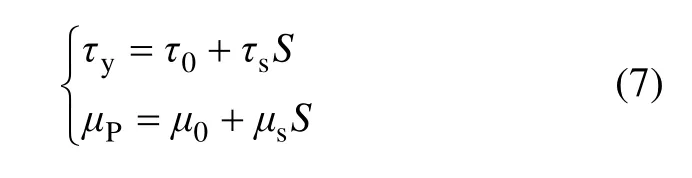
式中：τ0为絮网结构完全破坏时的屈服应力，Pa；τs絮网结构应力，Pa；μ0为絮网结构完全破坏时的塑性黏度，Pa/s；μs为絮网结构受剪过程中塑性黏度的变化值，Pa/s。

将式(7)代入式(6)则得到结构流管道阻力的计算公式为

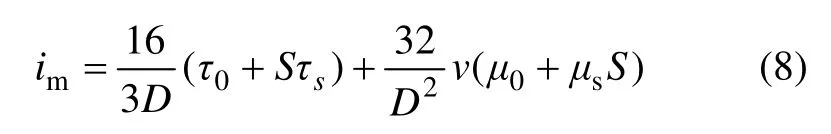
对于充填料浆长距离管道输送而言，其管阻损失im是指浆体稳定流动时的能量损失[20]，此时浆体结构达到平衡状态，结构系数S=Se，则由式(3)和(7)得：

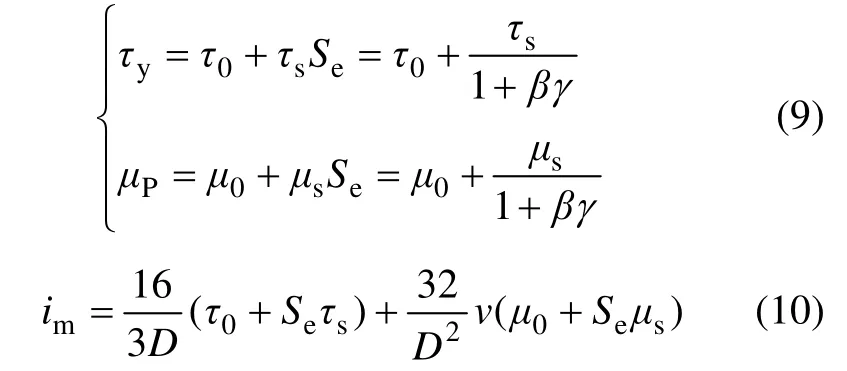
由式(9)可知：τy及μP均为剪切速率γ 的函数，其值随γ 增加，呈非线性递减，当剪切速率γ→∞，有τy=τ0，μP=μs。因此，在管道输送过程中，低流速条件下，浆体受剪切破坏程度较小，其屈服应力τy及塑性黏度值μP较大，随着流速增大，剪切对浆体絮网结构破坏越充分，其τy及μP相应减小。

将式(11)代入式(10)中，得到式(12)。对于同一浆体，当其输送管径D 一定时，式中A，B，τ0，τs，μ0，μs，β 等值不变，则管输阻力im为仅与流速v 相关的函数，但与不考虑浆体结构变化时(式6)不同，im与v不再是简单的线性关系，而表现为复杂的非线性关系。

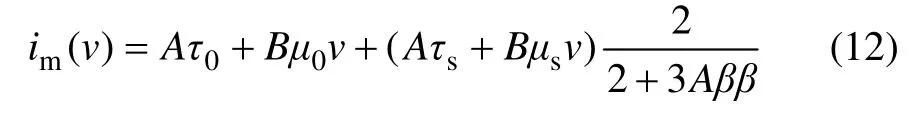
为了对im(v)的变化规律进行分析，将式(12)对流速v 求导，得：

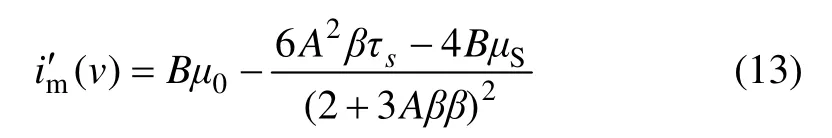
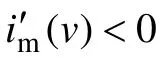
因此，当v=vx，im(v)存在最小值im(vx)，如图1 所示。则对于结构流体，随着流速v 的增加，管输阻力im呈先减小再增大的变化趋势，存在一最佳流速vx，在此条件下浆体输送的管道阻力最小。在实际生产过程中，可将此流速作为最合理的输送流速，从而降低系统能耗损失。

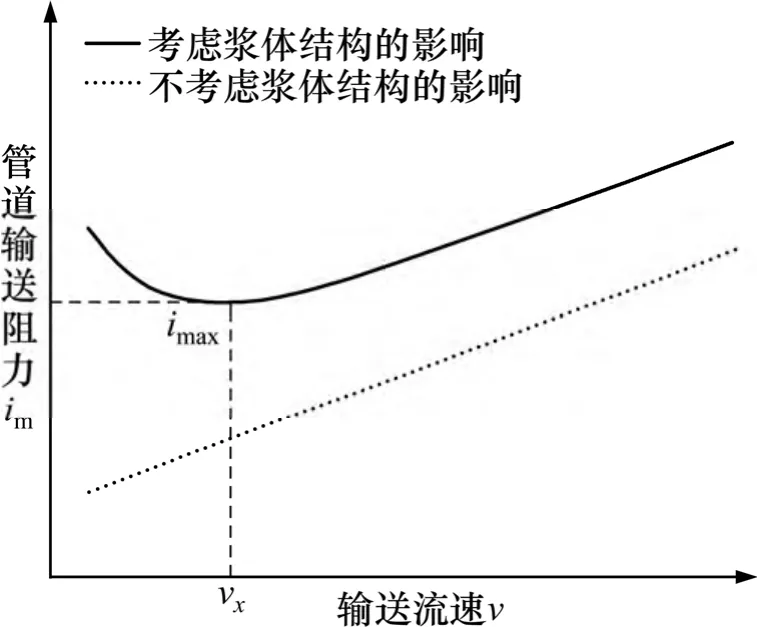
图1 管输阻力与输送流速的关系Fig.1 Relationships between resistance loss and flow velocity in pipeline transport

同时，由式(14)可知：对于某一确定浆体(即τ0，τs，μ0，μs和β 一定)，最佳流速vx为关于A 的函数，即与管径D 相关(A=16/(3D))，管径越大，则vx越大。究其原因，由式(1)分析得，欲使浆体受到相同的剪切作用(即γ 一定)，对于较大管径D，必须相应提高浆体流速v。

3 试验验证

3.1 试验材料

实验材料来源于国内某铅锌矿的充填膏体料浆，充填物料由选厂全粒级尾砂、冶炼水淬渣以及普通硅酸盐水泥组成[21]。全尾砂密度为2.71 t/m3，平均粒径为75.59 μm，其中＜20 μm 的颗粒累计含量占37.20%，比表面积为0.5 m2/cm2。水淬渣密度为2.59 t/m3，粒径主要为2 mm 左右，图2 所示为不同组分的粒级分布曲线。同时，全尾砂中含有浓密过程中残留的聚丙烯酰胺(PAM)阴离子型有机高分子絮凝剂(品牌SNF，型号AN934SH)，添加量为30 g/t。

图2 膏体物料粒级组成曲线Fig.2 Grain size curves of paste materials

3.2 试验设备及方案

为对浆体的管阻特性进行研究，设计了泵送环管试验系统。料浆制备采用2 台混凝土搅拌机进行2 段搅拌，人工计量上料。输送设备为一台HBT50.13.90S混凝土泵，数据采集系统采用电磁流量计、远传压力变送器、工控系统自动记录，监测数据利用“概率统计法”进行处理。选用输送管径为150 mm 及178 mm，试验系统管路总长度220 m。本文基于膏体泵送环管试验的部分监测数据，探讨不同物料组成、管径对其管阻特性的影响。考虑的充填物料主要包括：全尾砂、全尾砂+分级尾砂、(m(全尾砂):m(分级尾砂)=3:1)以及全尾砂+水淬渣(m(全尾砂):m(水淬渣)=3:1) 3 种配比方案，均按照1:8 的灰砂质量比与水泥均匀拌合，浆体质量分数为78%～80%，系统流量为20～80 m3/h。

3.3 试验结果分析

3.3.1 物料组成对管阻损失的影响

图3 所示为3 种不同物料浆体管阻损失im随流速v 的变化规律。由图3 可知：im随v 增大，均呈现先降低再增大的趋势，存在最佳流速vx，此条件下im有最小值。观察发现，不同物料条件下的最佳流速vx各不相同，这是由于不同物料组成导致浆体流变性质各异，从而引起vx变化。相比之下，“全尾砂+分级尾砂”、“全尾砂”3 种物料组合模式下最佳流速vx偏小，在此条件下虽能降低系统能耗损失，但充填效率较低，难以满足生产要求。而采用“全尾砂+水淬渣”时，其最佳流速在0.7～0.8 m/s 之间，对应流量为60～70 m3/h，可满足矿山充填要求。

3.3.2 管径对管阻损失的影响

图4 所示为质量分数为80%，全尾砂+水淬渣，灰砂质量比为1:8 的膏体料浆在150 mm 及178 mm 2种管径条件下的阻力特性。由图4 可知：随着流速v增大，其管阻损失im均呈现出先减小再增大的趋势。在管径为150 mm 的管道中，当流速v 在0.5～0.6 m/s范围内，其摩阻损失有最小值，约为2.2 MPa/km；而对于管径为178 mm 管道中，管阻损失在0.7～0.8 m/s范围内有最小值1.87 MPa/km。相比之下，管径178 mm时的最佳流速比管径150 mm 的大，这与前述理论分析结果一致。结果表明：对于该充填膏体，采用管径178 mm，流速为0.7～0.8 m/s 时，其管阻损失im为1.87 MPa/km 左右，且充填能力达60～70 m3/h，为系统最佳输送参数。

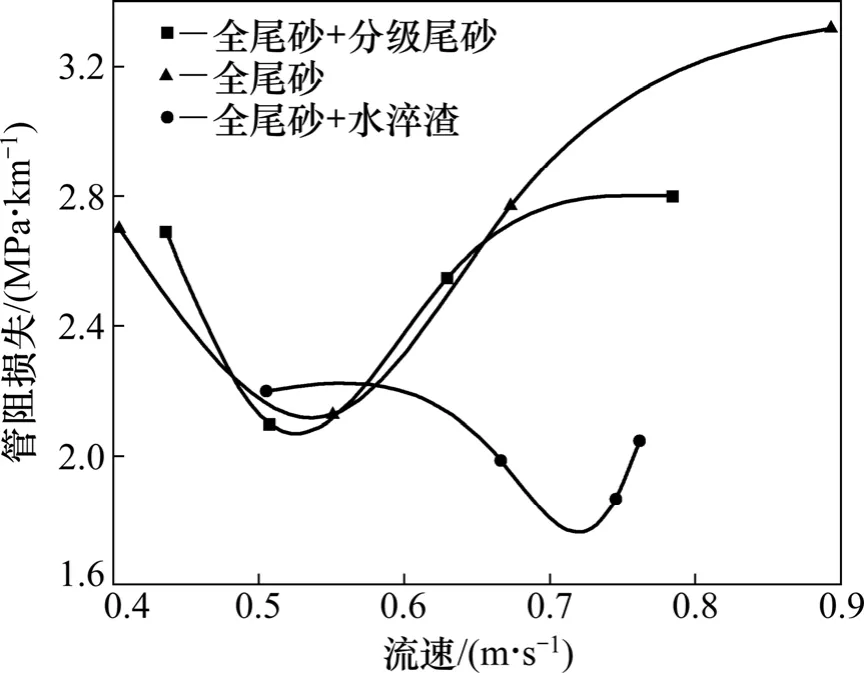
图3 物料组成对管阻损失的影响Fig.3 Effects of material content on resistance loss

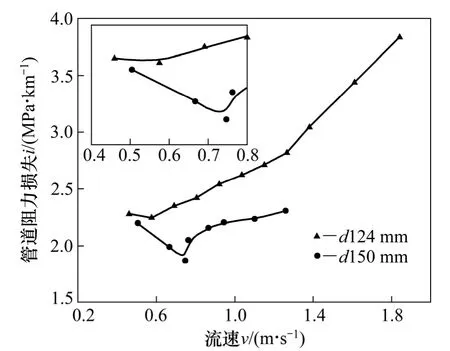
图4 管径对管阻损失的影响Fig.4 Effects of pipe diameter on resistance loss

4 结论

1) 膏体充填料浆中存在三维絮网结构，呈结构流流动，浆体流变性质及管道输送阻力特性与其内部结构状态紧密相关。

2) 在不同剪切作用下，结构破坏程度不同，由此导致浆体流变性质的变化，剪切速率越大，其屈服应力及塑性黏度值相应越小。

3) 对于结构流充填料浆，随流速增大，其管道阻力损失im呈先减小再增大的变化趋势，存在最佳流速vx，在此条件下，其管道阻力im有最小值。vx主要受浆体流变性质及输送管径D 的影响，D 越大，则vx越大，此结论为管道输送参数优化提供了一种新的思路。

4) 基于某铅锌矿充填膏体泵送环管实验数据，分析了物料组成及输送管径两因素对管阻特性的影响，结果验证了前述结论，同时表明：对于该矿的全尾砂+水淬渣膏体，采用管径178 mm，流速为0.7～0.8 m/s时，其管阻损失im为1.87 MPa/km 左右，且充填能力达60～70 m3/h，为系统合理输送参数。

[1] 周爱民, 古德生. 基于工业生态学的矿山充填模式[J].中南大学学报(自然科学版), 2004, 35(3): 468-472.ZHUO Aimin, GU Desheng. Mine-filling model based on industrial ecology[J]. Journal of Central South University(Science and Technology), 2004, 35(3): 468-472.

[2] YUAN Yao, ZENG Dicui, RU Zhouwu. Development and challenges on mining backfill technology[J]. Journal of Materials Science Research, 2012, 1(4): 73-78.

[3] 韩斌, 吴爱祥, 王贻明. 低强度粗骨料超细全尾砂自流胶结充填配合比优化及应用[J].中南大学学报(自然科学版), 2012,43(6): 2357-2362.HAN Bin, WU Aixiang, WANG Yiming. Optimization and application of cemented hydraulic fill (CHF) with low strength aggregate and extra fine grain full tailings[J]. Journal of Central South University (Science and Technology), 2012, 43(6):2357-2362.

[4] Zbik M S, Smart R S C, Morris G E. Kaolinite flocculation structure[J]. Journal of Colloid and Interface Science, 2008,328(1): 73-80.

[5] 姚中亮. 全尾砂结构流体胶结充填的理论与实践[J].矿业研究与开发, 2006(增刊1): 15-18.YAO Zhongliang. Theory of and practice in cemented filling with unclassified tailings structure fluid[J]. Mining Research and Development, 2006(Suppl 1): 15-18.

[6] WANG Xinmin, LI Jianxiong. Rheological properities of tailing paste slurry[J]. Journal of Central South University of Technology, 2004, 11(1): 75-81.

[7] 翟永刚, 吴爱祥, 王洪江, 等. 全尾砂膏体料浆的流变特性研究[J]. 金属矿山, 2010(12): 30-32, 57.ZHAI Yonggang, WU Aixiang, WANG Hongjiang, et al. Study on rheological properties of the unclassified-tailings paste[J].Foreign Metal Mining Magazine, 2010(12): 30-32, 57.

[8] 王劼, 杨超, 张军, 等. 膏体充填管道输送阻力损失计算方法[J]. 金属矿山, 2010(12): 34-36.WANG Jie, YANG Chao, ZHANG Jun, et al. Calculation method of the resistance loss in pipeline transportation of paste filling slurry[J]. Foreign Metal Mining Magazine, 2010(12): 34-36.

[9] 张宗生. 金川矿山废石膏体配制与流变特性研究[D]. 昆明:昆明理工大学国土资源工程学院, 2008: 47-49.ZHANG Zongsheng. Study on preparation and rheological characteristics of waste rock paste in Jinchuan Mine[D].Kunming: Kunming University of Science and Technology.Faculty of Land Resource Engineering, 2008: 47-49.

[10] 王五松. 膏体充填流变特性及工艺研究[D]. 阜新: 辽宁工程技术大学矿业学院, 2004: 36-37.WANG Wusong. Study on the rheological characteristics and technology in paste backfilling[D]. Fuxin: Liaoning Technical University. College of Mining Engineering, 2004: 36-37.

[11] Hallbom D J, Klein B. Flow array for nickel laterite slurry[C].TMS International Nickel Symposium, Charlotte NC, 2004:415-428.

[12] 詹钱登, 郭峰豪, 郭启文. 泥浆体应力松弛特性之实验研究[J]. 农业工程学报, 2009, 55(3): 65-74.ZHAN Qiandeng, GUO Fenghao, GUO Qiwen. Experimental study on the characteristics of stress relaxation of mud slurries[J].Journal of Taiwan Agricultural Engineering, 2009, 55(3): 65-74.

[13] 韩文亮. 细颗粒浆体的应力松弛模型[J]. 泥沙研究, 1991(3):87-92.HAN Wenliang. The stress relaxation model of fine particle slurry[J]. Journal of Sediment Research, 1991(3): 87-92.

[14] 费祥俊. 浆体与粒状物料输送水力学[M]. 北京: 清华大学出版社, 1994: 117-130.FEI Xiangjun. Slurry and granular material transport hydraulics[M]. Beijing: Tsinghua University Press, 1994:117-130.

[15] Jarny S, Roussel N, Le Roy R, et al. Modelling thixotropic behavior of fresh cement pastes from MRI measurements[J].Cement and Concrete Research, 2008, 38(5): 616-623.

[16] Wallevik J E. Rheological properties of cement paste:Thixotropic behavior and structural breakdown[J]. Cement and Concrete Research, 2009, 39(1): 14-29.

[17] Toorman E A. Modelling the thixotropic behaviour of dense cohesive sediment suspensions[J]. Rheologica Acta, 1997, 36(1):56-65.

[18] Cheng D C H. A differential form of constitutive relation for thixotropy[J]. Rheologica Acta, 1973, 12(2): 228-233.

[19] Worrall W E, Tuliani S. Viscosity changes during the ageing of clay-water suspensions[J]. Trans Brit Ceramic Soc, 1964, 63(6):167-185.

[20] 吴爱祥, 刘晓辉, 王洪江,等. 考虑时变性的全尾膏体管输阻力计算[J]. 中国矿业大学学报, 2013, 42(5): 736-740.WU Aixiang, LIU Xiaohui, WANG Hongjiang, et al. Calculation of resistance in total tailings paste piping transportation based on time-varying behavior[J]. Journal of China University of Mining Technology, 2013, 42(5): 736-740.

[21] 刘晓辉, 吴爱祥, 王洪江, 等. 深井矿山充填满管输送理论及应用[J]. 北京科技大学学报, 2013, 35(9): 1113-1118.LIU Xiaohui, WU Aixiang, WANG Hongjiang, et al. Full-flow transport theory and its application in deep mine backfilling[J].Journal of University of Science and Technology Beijing, 2013,35(9): 1113-1118.