大功率风力发电机在独立变桨控制下的振动研究

金鑫，熊海洋，夏宗朝，何玉林，杜静

(重庆大学 机械工程学院，重庆，400044)

随着风力抗阻容量、风轮直径、塔架高度的增加，其振动问题逐渐呈现出来，由其导致的运行失效问题也时有发生。国内外学者已进行了大量相关研究。Arrigan 等[1]采用一种半主动的调质阻尼器来实时地降低叶片拍打方向的振动。Staino 等[2]提出一种主动控制器来减小叶片弦向振动的方法。Manzato 等[3]获得了实际尺寸风机的各阶模态，并与多体动力学仿真结果进行比较。软件预测的低阶模态与实验结果吻合的很好，高阶模态的差异要大一些。Al Ahmar 等[4-5]介绍了一种新的信号处理方法，以更好地监测和诊断风机传动链上振动引起的故障。任彦忠等[6-7]通过在塔顶安装加速度传感器，测出了塔架的固有频率。并将其与有限元分析得出的结果进行比较，验证了有限元分析的可行性。何玉林等[8-9]针对变桨控制是传动链阻尼很小导致齿轮箱较大转矩振动的问题，作者通过在原有的转矩给定值上附加一个与转矩振动反相的转矩波动，以增加传动链的等效阻尼，从而抑制传动链的转矩振动。国内外对风机振动的研究主要集中在对振动的测试、分析以及振动的控制上。独立变桨控制是近年来新兴的风力发电控制技术，其工作原理是在叶片不同位置采用不同的桨矩角，实现气动载荷被“削峰填谷”，其波动被削弱，使关键结构的振动及疲劳载荷降低[10-14]。本文提出基于线性二次型调节(LQR)和干扰自适应控制(DAC)技术的独立变桨控制策略，研究独立变桨下风电机组的振动情况。

1 风力机组基本运行控制原理

1.1 基本运行区域

典型的变桨变速风电机组有不同的运行区域，如图1 所示。当系统检测到风速达到启动值时，系统通过发电机转矩控制叶轮转速，保持最佳尖速比达到最大功率吸收，直到风速达到额定风速，如区域Ⅰ所示；当风速继续增大；系统将实现变桨控制，使发电机功率保持为额定恒定值；如区域Ⅲ所示。区域Ⅱ为区域Ⅲ与Ⅰ的过渡区域。

图1 风力机的基本运行区域Fig.1 Basic operation area of wind turbines

1.2 风力机的运行控制策略

1.2.1 在额定风速以下的控制

风速在额定风速以下时，通过控制发电机的转矩使风力发电机尽量获取多的能量，其控制细节如图2所示。

1.2.2 在额定风速以上的控制

风速在额定风速以上时，通过变桨距使发电机输出的功率维持在额定功率附近。

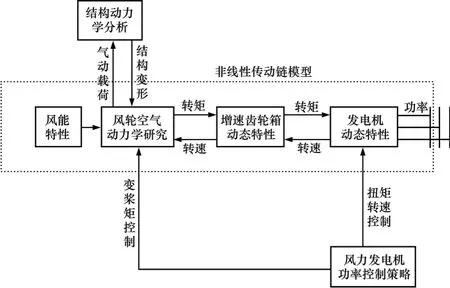
图2 风力发电机组的能量转换系统Fig.2 Energy conversion system of wind turbine

2 变桨控制器的设计

本文采用的变桨控制思想在统一变桨的基础上增加独立变桨控制，对风电机组运行在区域Ⅲ时进行控制，以削弱系统的气动载荷波动，叶片的实际桨距角表示为

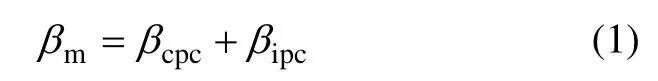
式中：βm为桨距需求；βcpc为统一变桨分量；βipc为独立变桨分量。控制框图如图3 所示。

图3 控制器框图Fig.3 Diagram of controller

3 独立变桨控制器的设计

线性二次型调节(LQR)是现代控制理论中发展最早也最为成熟的一种状态空间设计方法，它以状态空间形式的线性系统为对象，以对象状态和控制输入的二次型函数为目标函数。通过构造反馈增益G 在较低的控制成本下实现原系统较好的性能指标。线性二次型问题的最优解可写成统一的解析表达式和实现求解过程的规范化，并简单地采用状态线性反馈控制构成闭环最优控制系统，能够兼顾多项性能指标，因此得到特别的重视，为现代控制理论中发展较为成熟的一部分[15]。

一般风电机组的线性时不变状态空间模型为

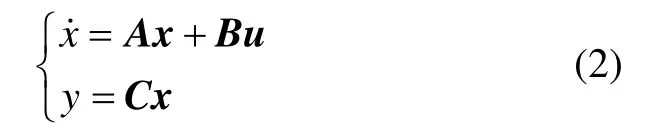
构建目标函数：

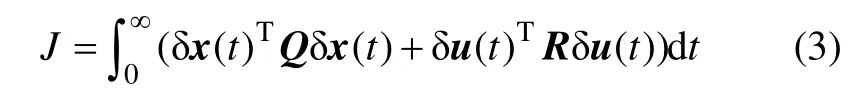
式中：δx(t)为系统状态；δu(t)为控制输入；Q 为状态权重矩阵；R 为输入权重矩阵。由最优控制理论知，反馈增益矩阵由下式计算：

式中：R-1为R的逆；BT为B的转置；P为黎卡提(Ricatti)方程的对称正定解，

在此基础上可构建反馈法则：u(t)=Gx(t)。

LQR 方法计算出来的反馈增益矩阵G 是基于系统的全状态反馈而得到的，但在工程实际中测量系统所有的状态是不经济甚至不可行的，因此，有必要引入状态观测器来估计状态变量的值。系统的可观测性是实现观测器设计的必要条件。状态观测器的数学模型表达式为

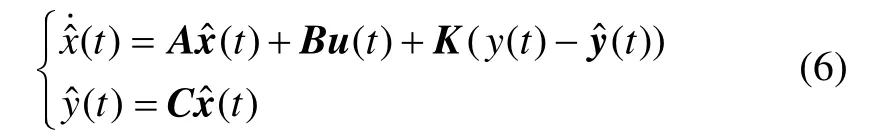
干扰自适应控制(DAC)是一种降低或抵消持续干扰的方法。它的基本思想是在状态观测器中引入干扰状态，将重构的干扰状态引入反馈增益中以抵消干扰输入的影响。这些干扰状态作为反馈控制的一部分被用来适应或抵消任何持续的干扰影响。

干扰模型可以假定为以下状态空间形式：

将式(4)经泰勒公式展开之后可得到表达式如下：

其中：ω 为叶轮旋转角度，单位为rad/s；AD为1 个与叶轮方位角无关的常量。

可得扰动输入矩阵和干扰状态矩阵：

采用的状态观测器和干扰自适应控制结构如图4所示。

图4 状态观测器与干扰自适应控制的控制框Fig.4 Control diagram of state estimator and DAC

4 仿真实验

为验证方法有效性，采用美国国家可再生能源实验室(NREL)开发的FAST 软件与Matlab7.1/Simulink进行联合仿真，算例采用NREL 5 MW 风力发电机为对象，模型数据[16]经过NREL 验证，其主要参数如表1 所示。

通过FAST 软件将风力发电机在运行点W=18 m/s，Ω0=12.1 r/min，β0=14.74°处进行线性化得到系统模型的状态空间矩阵；然后，使用LQR 技术和DAC技术对控制策略进行设计。图5 所示为MATLAB 中搭建的风机控制系统模型。

4.1 载荷分析比较

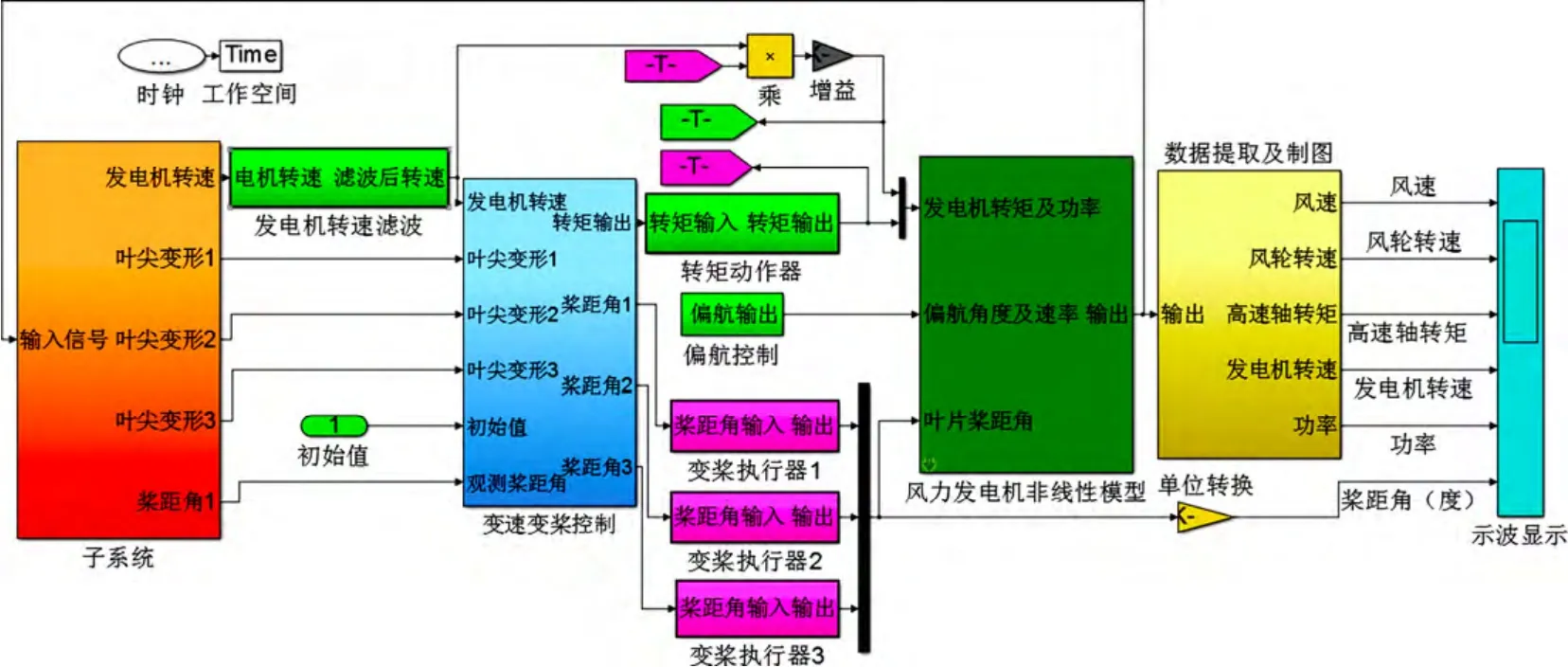
图5 Simulink 整体控制模型Fig.5 Simulink overall control model

图6 各工况下叶根的等效疲劳载荷Fig.6 Equivalent fatigue loads in all load cases

参数 取值额定功率/MW 5叶片长度/m 61.5风轮直径/m 80切入/切出风速/(m·s-1) 4～25额定风速/(m·s-1) 11.5风轮额定转速/(r·min-1) 12.1发电机额定转矩/(kN·m) 43.093 5发电机额定转速/(r·min-1) 1 173.7

风电机组机械振动主要来自于叶片、齿轮箱和电机。因此，将5 MW 风力发电机分别进行统一变桨和独立变桨情况下的叶根载荷、齿轮箱转矩和电机转矩进行分析。图6 所示为叶根在各种工况下的等效疲劳载荷。从分析结果来看，独立变桨可以有效降低风力发电机的振动载荷激励。图7 和8 分别所示为齿轮箱转矩和电机转矩。从分析结果看，独立变桨较统一变桨下的转矩载荷波动程度大幅度减小，能够更好的稳定在额定值。

4.2 振动计算比较

叶片及机舱是风电机组振动最明显的区域。2 种控制策略下的振动情况计算结果如图9～12 所示。从计算结果来看：风力机各项振动加速度幅值均有较大程度降低，通过独立变桨，可有效降低风力发电机振动。

图7 主轴转矩比较Fig.7 Comparison of main shaft torque

图8 发电机转矩比较Fig.8 Comparison of generator torque

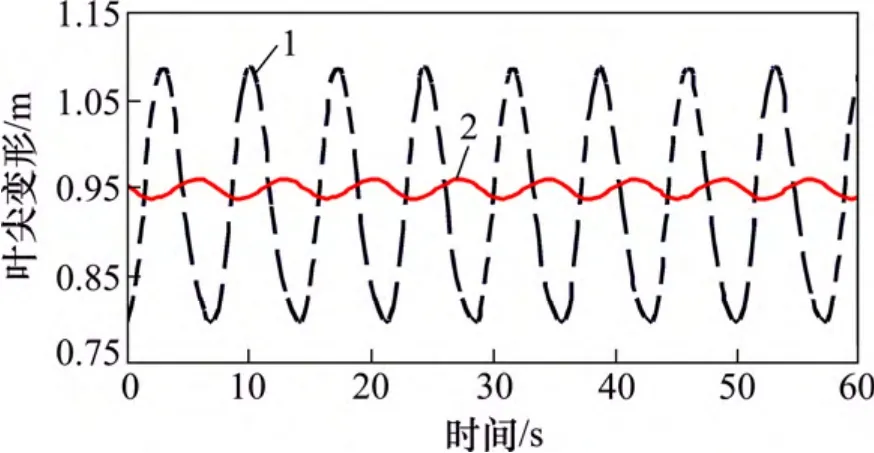
图9 叶尖变形比较Fig.9 Comparison of tip deformation

图10 机舱x 方向振动加速度比较Fig.10 Comparison of nacelle vibration acceleration in x-direction

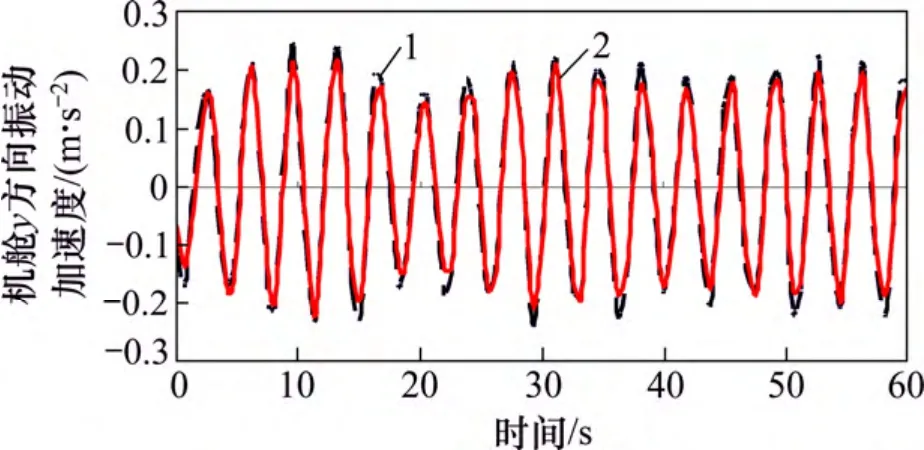
图11 机舱y 方向振动加速度比较Fig.11 Comparison of nacelle vibration acceleration in y-direction

图12 机舱俯仰加速度比较Fig.12 Comparison of nacelle pitch acceleration

5 结论

1) 提出基于线性二次型调节（LQR)结合干扰自适应控制 (DAC)技术的独立变桨控制策略，能够较好地实现独立变桨效果。

2) 通过载荷分析比较来看，独立变桨相较于统一变桨载荷的平均值虽然没有太大变化，但极大地降低了波动幅度。通过独立变桨，可以有效降低风电机组的振动载荷激励。

3) 通过振动分析比较，由于振动载荷激励得到有效降低,通过独立变桨，系统结构的各项振动加速度幅值均有较大程度下降。因此，通过独立变桨，可有效地降低风力发电机振动，从而可以提高设备可靠性，延长设备使用寿命。

[1] Arrigan1 J， Pakrashi V. Control of flapwise vibrations in wind turbine blades using semi-active tuned mass dampers[J]. Struct Control Health Monit, 2011, 18(8): 840-851.

[2] Staino A, Basu B, Nielsen S R K. Actuator control of edgewise vibrations in wind turbine blades[J]. Journal of Sound and Vibration, 2012, 331(6): 1233-1235.

[3] Manzato1 S, Peeters B.Wind turbine model validation by full-scale vibration test[R]. NREL/TP-500-35816, 2008.

[4] Al Ahmar E, Choqueuse V. Advanced signal processing techniques for fault detection and diagnosis in a wind turbine induction generator drive train: A comparative study[J]. Energy Conversion Congress and Exposition (ECCE),2010, 32(8): 3576-3581.

[5] 余熳烨, 林颖, 胡清明. 双馈风力发电机组振动问题分析与处理[J]. 机床与液压, 2010, 38(9): 143-148.YU Manye, LIN Ying, HU Qingming. Analysis and solution of the vibration fault of dual-feedback wind turbine[J]. Machine Tool & Hydraulics, 2010, 38(9): 143-148.

[6] 任彦忠, 王川. 某风电场风力发电机组振动故障探究[J]. 新能源, 2011, 44(3): 86-89.REN Yanzhong, WANG Chuan. Study on WTG faults caused by turbine vibration[J]. Electric Power, 2011, 44(3): 86-89.

[7] 高俊云, 连晋华. 发电机组塔筒振动的分析与测量[J]. 风能,2011(2): 54-56.GAO Junyun, LIAN Jinhua. Analysis and measure for wind turbine tower[J]. Wind Energy, 2011(2): 54-56.

[8] 何玉林, 苏东旭, 黄帅. 变速变桨风力发电机组的桨距控制及载荷优化[J]. 电力系统保护与控制, 2011, 39(16): 95-100.HE Yulin, SU Dongxu, HUANG Shuai. Pitch control and load optimization of variable speed variable pitch wind turbine[J].Power System Protection and Control, 2011, 39(16): 95-100.

[9] 宋新甫, 梁波. 基于模糊自适应 PID 的风力发电系统变桨距控制[J]. 电力系统保护与控制, 2009, 37(16): 50-53.SONG Xinfu, LIANG Bo. Wind power system pitch control based on fuzzy self-learning emendation control theory[J].Power System Protection and Control, 2009, 37(16): 50-53.

[10] 何玉林, 刘军, 李俊. 变速变桨距风力发电机组控制策略优化[J]. 电力系统保护与控制, 2011, 39(12): 55-60.HE Yulin, LIU Jun, LI Jun. Pitch control and load optimization of variable speed variable pitch wind turbine[J]. Power System Protection and Control, 2011, 39(12): 55-60.

[11] Bossanyi E. Individual blade pitch control for load reduction[J].Wind Energy, 2003, 6(2): 119-128.

[12] Bossanyi E. Wind turbine control for load reduction[J]. Wind Energy, 2003, 6(3): 229-244.

[13] Jonkman J M, Buhl M L. FAST User’s Guide[R]. Golden, CO:National Renewable Energy Laboratory, NREL/EL-500-38230,2005.

[14] 樊艳芳, 晁勤, 高瑜, 等. 大型双馈式变速恒频发电机组对电网影响仿真分析[J]. 电力系统保护与控制, 2008, 36(16):30-32.FAN Yanfang, CHAO Qin, GAO Yu, et al. Simulation of influence of large double-fed variable speed wind turbine into grid[J]. Power System Protection and Control, 2008, 36(16):30-37.

[15] 薛定宇. 反馈控制系统设计与分析[M]. 北京: 清华大学出版社, 2000: 298-299.XUE Dingyu. Feedback control system design and analysis[M].Beijing: Tsinghua University Press, 2000: 298-299.

[16] Jonkman J, Butterfield S, Musial W, et al. Definition of a 5-MW Reference Wind Turbine for Offshore System Development[R].NREL/TP-500-38060, Golden, CO: National Renewable Energy Laboratory, January 2006.