大理岩在高应力状态下受小幅循环动力扰动的力学试验

唐礼忠，武建力，刘涛，朱俊，舒计步

(中南大学 资源与安全工程学院，湖南 长沙，410083)

岩体工程开挖在其围岩中产生应力重新分布并经常受到邻近工程开挖的动力作用。矿山开采常常是多采场、多巷道和多步骤开采活动，是一种典型的围岩长期受到邻近开挖影响的岩体工程。开挖空间的形成和改变造成围岩处于不断的应力集中及应力转移动态变化状态，采场爆破和较大的岩层动力失稳破坏对采区岩体产生频繁的动力作用。在深部开采矿山，岩体地应力很高，深部开采中工程围岩处于很高的应力状态和频繁的动力作用可能是深部开采矿山岩爆的重要成因，因此，开展高应力状态和频繁动力作用下岩石力学行为的研究已受到采矿岩石力学界的高度重视[1-2]，成为学术界和工程应用的重要课题。矿山采场和巷道围岩受到的动力作用主要表现为爆破产生的冲击波、应力波和地震波不同形式，这主要与受动力作用的工程围岩与爆破源的位置有关，紧邻爆破源的围岩受冲击波作用、邻近爆破源的工程围岩受到应力波作用而离爆破源较远处的工程围岩受到地震波的作用，后者与较大的岩体破坏产生的地震波类似。较低频率的地震波传播的距离较远其携带的能量也较大，因此，低频地震波对岩体的破坏作用更大。矿山开采爆破和岩体破坏产生的地震波的低频部分可达几赫兹至几十赫兹频段[3]。因此，作为室内试验研究，可以在试验机上进行循环加卸载试验来模拟低频地震波对岩石的作用条件。对岩石在循环荷载下的力学性质，国内外已经做了很多研究，葛修润等[4-5]通过试验研究了岩石在循环荷载下破坏的极限变形规律和岩石在循环作用下发生破坏存在循环应力水平下限；陶振宇等[6-9]研究了上限应力、循环幅值、循环频率和加载波形对岩石循环加卸载的影响；文献[10-13]等从不同角度研究了岩石在循环作用下的损伤过程；左宇军等[14]对静载荷条件下岩石循环荷作用的力学特性；马春德等[15]对红砂岩做了双向受静载的动力扰动试验。但是，现有研究多为大循环加卸载，其加载上限应力都小于岩石静力强度，每次卸载接近于完全卸载，为常规的循环加卸载试验。在深部矿山中，工程开挖后造成的应力集中和应力重分布将导致很大范围内的岩体进入高应力状态甚至处于静力屈服阶段；爆破或岩体破坏产生的地震波对应的动力扰动幅值相对于岩石动力破坏强度往往较小，因此，在高应力静力作用状态下小幅振动的动力扰动是深部矿山岩体的一种重要受力形式；同时，这种小幅振动的动力与静力叠加可能超出岩体的静力极限强度。由此可见，研究同时高静应力和小幅振动的动力扰动作用条件下的岩石力学性质对于揭示深部开采矿山岩体力学行为具有重要的理论和实际意义，但是目前对此的研究较少。本文作者在现有试验条件的基础上，以冬瓜山铜矿深部栖霞组大理岩作为试验岩样，开展在一维高静应力条件下对试件施加其上限应力接近和超过静力强度极限的小幅循环动力扰动作用的力学试验，研究高应力状态下大理岩受小幅循环动力扰动作用的力学特性，为深部矿山开采岩体动力失稳破坏的控制提供理论依据。

1 试验设备及方案

本次试验在中南大学力学测试中心的MTS-322电液伺服静动万能试验机上进行，试验系统见图1。该系统只能施加单向荷载，轴向最大输出荷载为动态±500 kN，可实现循环频率为0～20 Hz。为实现岩石在一定静力作用下的循环动力扰动试验，首先以静力加载方式对岩石施加静力荷载，采用载荷控制，以一定的加载速度施加荷载，应力达到某预定值后，以此静应力为平均应力，施加周期性循环动力荷载，循环扰动时为了保持恒定的加载速率，采用载荷控制的方式加载，为模拟振动传播时的弹性波，循环扰动波形取正弦波形式，试验机以不变的上限荷载和下限荷载对岩石进行循环加载直至岩石破坏。加载过程和特征如图2 所示，其中，σmax为循环荷载的上限应力，σmin为循环荷载的下限应力，σΔ=σmax-σmin为应力幅值，σa=(σmax+σmin)/2 为平均应力，T 为周期。试验过程中试验系统可采集轴向荷载、轴向变形、横向变形和时间数据，并绘制相应参数关系曲线。

图1 试验设备Fig.1 Testing instrument

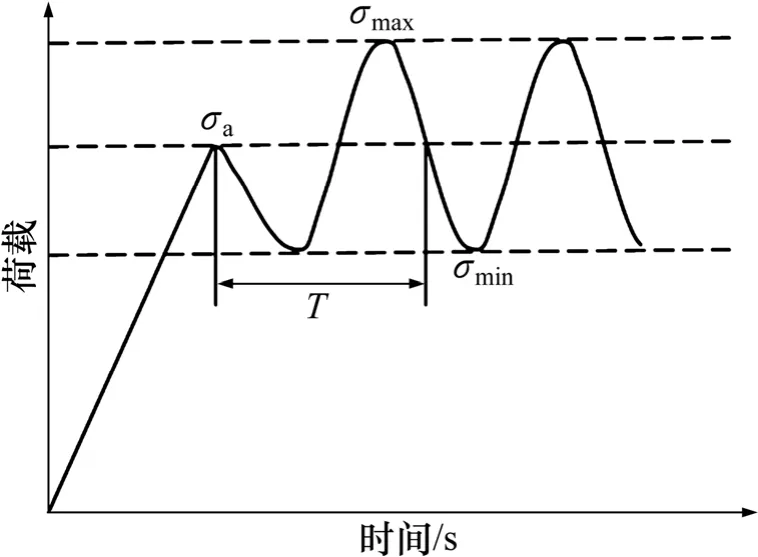
图2 循环荷载加载波形示意图Fig.2 Schematic of load wave of cyclic loading

本次试验研究的突出特点是高应力状态下受小幅循环动力扰动，试验首先需要选取合理的平均应力大小及循环动力扰动的循环幅值。为此进行了2 个预备性试验，即单轴抗压强度试验和应力水平试探性循环加载试验。本次试验所用岩样为冬瓜山铜矿-790 m 中段 61 线顶板的栖霞组大理岩，埋深840 m，灰色，颗粒较粗，矿物成分为方解石。为提高试验可比性，岩样钻取自同一块岩石。试样为直径40 mm、高100 mm的圆柱形试件，端面不平行度和不垂直度在0.03 mm以内。3 组单轴抗压强度验测得岩石单轴抗压强度的平均值为77.04 MPa，弹性极限(屈服强度)为60 MPa。应力水平试探性试验是在同一个试件上，通过从较小的平均应力水平开始施加循环荷载，然后逐级增大平均应力水平，直至试件在某个较高应力水平下循环破坏。该试验的初始平均应力设定为23 MPa，应力幅值始终保持为25 MPa，试验结果用于确定平均应力水平和应力上限。

为使试验既处于高应力水平条件，又有较高的成功率，平均应力考虑以屈服强度为底限，不宜选取过高应力水平。区别于现有岩石循环加卸载试验，本次试验要反映深部矿山开采条件下岩石处于高应力状态下受小幅振动的动力扰动的实际情况，因此，考虑到通常情况下，岩石的动力强度大于其静力强度，本次试验的静力和动力扰动组合的上限应力与岩石静力强度接近，部分上限应力大于岩石的静力强度；动力扰动的循环幅值较小，并考虑改变幅值，以研究岩石在不同幅值的循环动力扰动下的力学特性。对应的试验方案见表1。

1) 在不同的平均应力、相同的循环幅值条件下(方案1)，为实现高应力，平均应力水平选择等于或大于屈服强度(60 MPa)，取3 个平均应力水平即60，65和70 MPa，但循环幅值均为30 MPa(单轴抗压强度的38%)的小幅循环动力扰动荷载，进行3 组试验。可见，该试验中岩石受的荷载上限会出现超过岩石静力单轴抗压强度的情况。

2) 在平均应力水平不变，改变循环扰动应力幅值条件下(方案2)，选取平均应力为60 MPa(岩石屈服强度)，循环动扰动幅值分别为30，35 和50 MPa，进行3 组试验。

席道瑛等[8]对不同循环频率(5～15 Hz)循环动力加载试验表明，随着动力载荷的循环频率增高，岩石材料损伤加剧，导致材料强度降低，模量减小，但其变化规律是一致的。因此，本次试验采用循环动力扰动频率为5 Hz，可在一定程度上模拟矿山地震活动低频部分的特征，使试验结果具有代表性。

2 试验结果及分析

按照试验方案，通过MTS 试验系统测得了岩石在循环动力扰动作用下的完整的应力-应变曲线以及相关的试验特性参数。图3 所示为DH-4 大理岩试件的应力-应变曲线。从图3 可以看出：大理岩先静力加载到60 MPa，然后以30 MPa 的应力幅值循环扰动，此时岩石的轴向应变随着荷载的变化而循环变化。这一过程中，岩石轴向应变不断的累积增大，当轴向应变达到岩石的破坏极限时，岩石破坏。通常点c 以后，岩石应力不会再达到上限应力，习惯上把该点称为极限应变点[6]，正弦荷载1 个周期称为1 次循环。试验结果见表1。

2.1 循环动力扰动的应力上限与强化作用

在试探性循环试验中，对大理岩试件先加载到较低的平均应力(23 MPa)，然后以较小的应力幅值(25 MPa)循环加载，加载1 000 次后岩石基本没有变化，然后荷载卸至0 MPa，提高平均应力至38 MPa 再次循环加载，如此多次增大平均应力，至平均应力为61 MPa 时，岩石最终在循环加载条件下破坏。图4 所示为对应力-应变曲线进行处理后得到应力水平、循环数和轴向应变的关系。较低平均应力时，在循环荷载作用下，岩石轴向应变以很小的量增加，最后基本保持不变。平均应力提高，静力加载产生的轴向应变增大，但在循环荷载作用下轴向应变仍然增大较小的值。可见，小幅值动力扰动下上限应力在没有达到一定的值前，大理岩不会破坏。这与常规循环试验结果一致，岩石循环加载破坏存在应力门槛值[4]。

图3 应力-应变曲线(试件DH-4)Fig.3 Axial stress-strain curve (specimen DH-4)

表1 大理岩循环动力扰动试验方案Table 1 Scheme of mechanics experiments of marble under circle dynamic disturbance

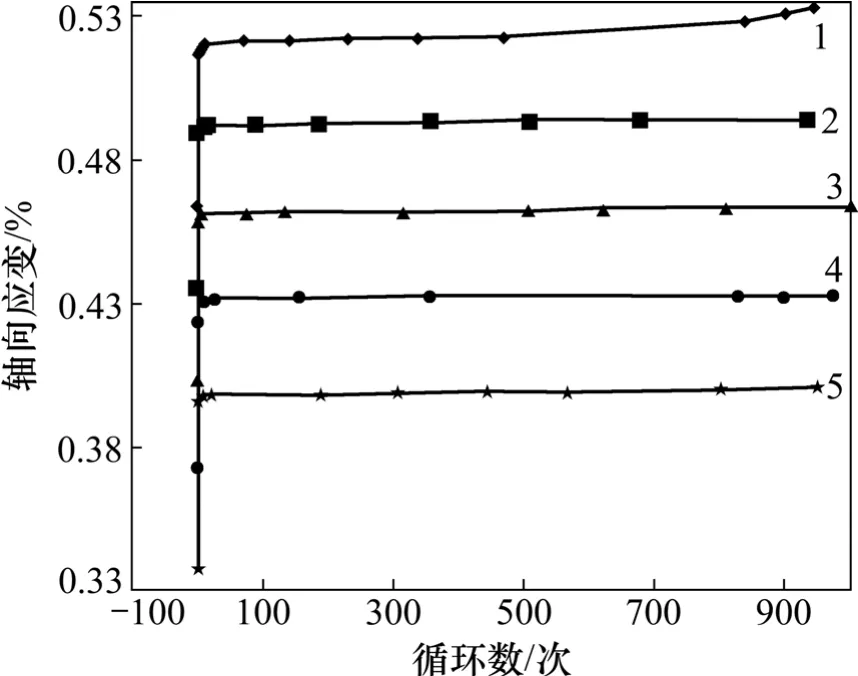
图4 应变-循环数关系曲线(试件DH-2)Fig.4 Relationships between axial strain and cyclic times(specimen DH-2)

每次重新加载的静力加载岩石的弹性模量与对应的平均应力关系如图5 所示。由图5 可见：随着平均应力的提高，岩石的弹性模量增加。在未达到门槛应力之前，循环荷载对岩石并非没有影响，循环荷载对岩石有强化作用，第6 次加载时的弹性模量比第1 次提高了43%。弹模的增加的原因首先是上一阶段的循环加载使岩石内的节理裂隙压密闭合，使得岩石刚度变大；其次，本试验选用的是粗晶大理岩，大理岩晶粒之间裂隙较多，受到循环荷载时大理岩晶粒破坏脱落充填到附近的空隙，提高了裂隙间的摩擦力，从而提高了大理岩的弹性模量。

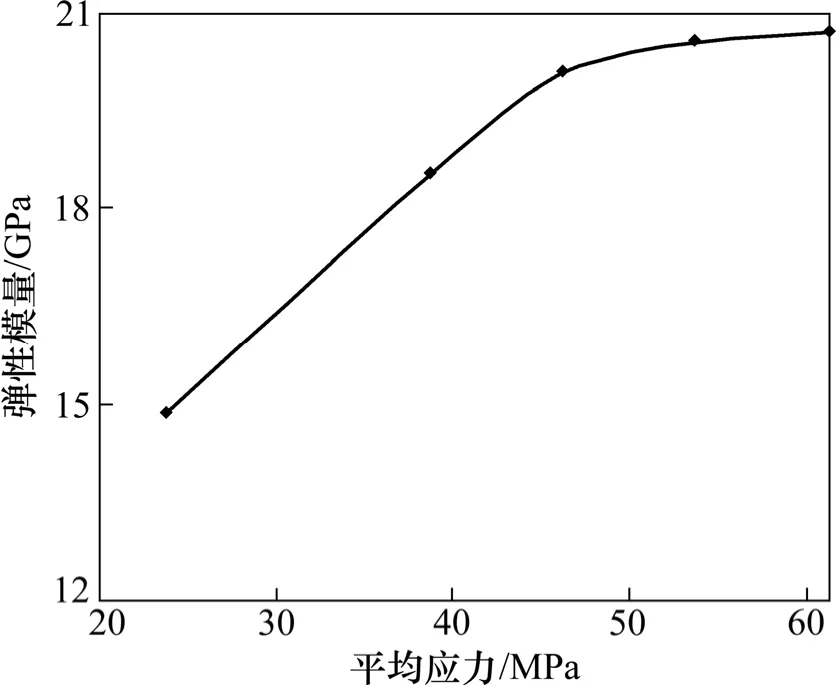
图5 弹性模量-平均应力关系曲线(试件DH-2)Fig.5 Relationships between elastic modulus and average of cyclic load (specimen DH-2)

2.2 循环动力扰动下平均应力对岩石破坏的影响

试验方案1 为循环应力幅值为30 MPa，平均应力分别为60，65 和70 MPa 3 组循环动力扰动试验。3组试验的3 个典型试件的应力-应变曲线分别如图3和6 所示。比较3 个试件的轴向应力-应变曲线发现，每个循环加卸载周期的变形量随着平均应力的提高而增加，表明在每个周期中有更多的能量损耗，岩石的损伤更大，产生的不可逆变形也越大。这3 组试验试件破坏的平均动力扰动循环数分别为458，121 和4，可见，试件破坏需要的动力扰动循环数随平均应力增大而快速减少。另外，这3 组试验测得3 种平均应力下岩石循环加卸载阶段的总应变的平均值分别为0.239%，0.214%和0.213%，相差不大，这表明岩石在循环动力扰动下的破坏需要达到一定的变形量时才会发生。

2.3 应力幅值和加载上限应力对岩石破坏的影响

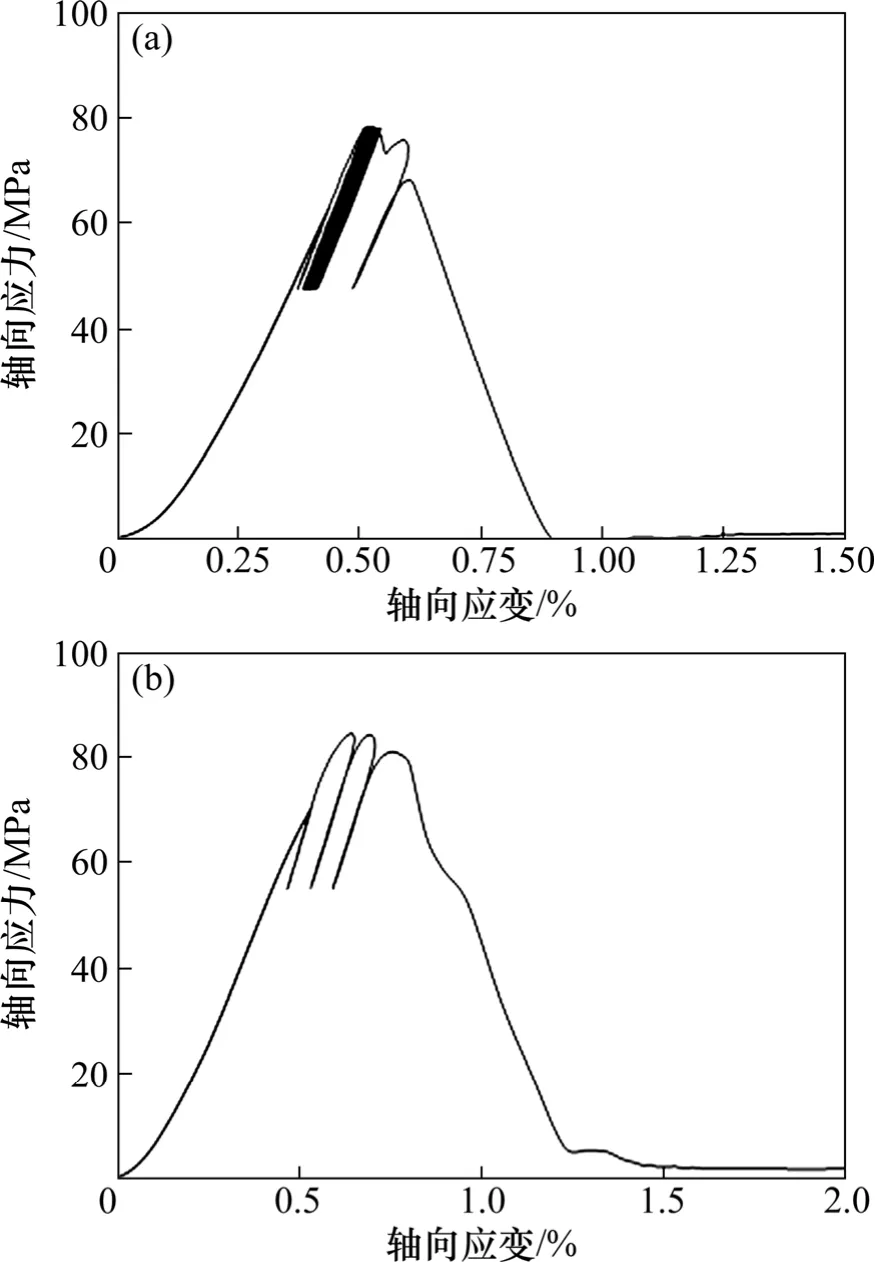
图6 应力-应变曲线Fig.6 Axial stress-strain curves

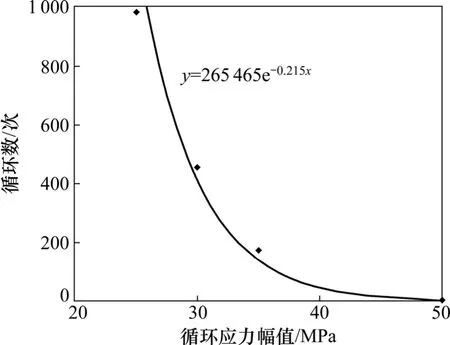
图7 循环扰动幅值与循环数的关系曲线Fig.7 Relation curves of cyclic numbers-stress amplitude

试验方案2 中，在平均应力水平为60 MPa 的条件下进行了扰动应力幅值分别为30，35 和50 MPa 等3 组不同的应力幅值的循环动力扰动试验。在试探性循环试验中当平均应力为61 MPa(扰动应力幅值为25 MPa)时岩石最终发生破坏。扰动应力幅值为25，30，35 和50 MPa 的4 组试验中岩石最后发生破坏的平均循环数分别为983，458，176 和3，绘制这4 组试验试验破坏循环数与循环应力幅值关系如图7 所示。由图7 得拟合关系式(见图7)，表明在一定应力水平下，随着循环动力扰动的幅值增大岩石破坏需要的循环数减小，并呈指数降低。

本次试验中，循环应力幅值为25，30，35和50 MPa对应的加载应力上限与岩石静力单轴抗压强度之比即表1 所示上限应力比分别为95%，97%，104%和110%，绘制加载应力上限比与破坏循环数关系曲线如图8 所示。试验结果显示，上限应力与循环数呈指数关系，其拟合关系如图8 所示，上限应力超过岩石静力强度后循环数显著下降，岩石在动力扰动作用下极易破坏。因此，岩石在动力扰动条件下，加载上限应力对岩石破坏的循环数也具有明显影响。

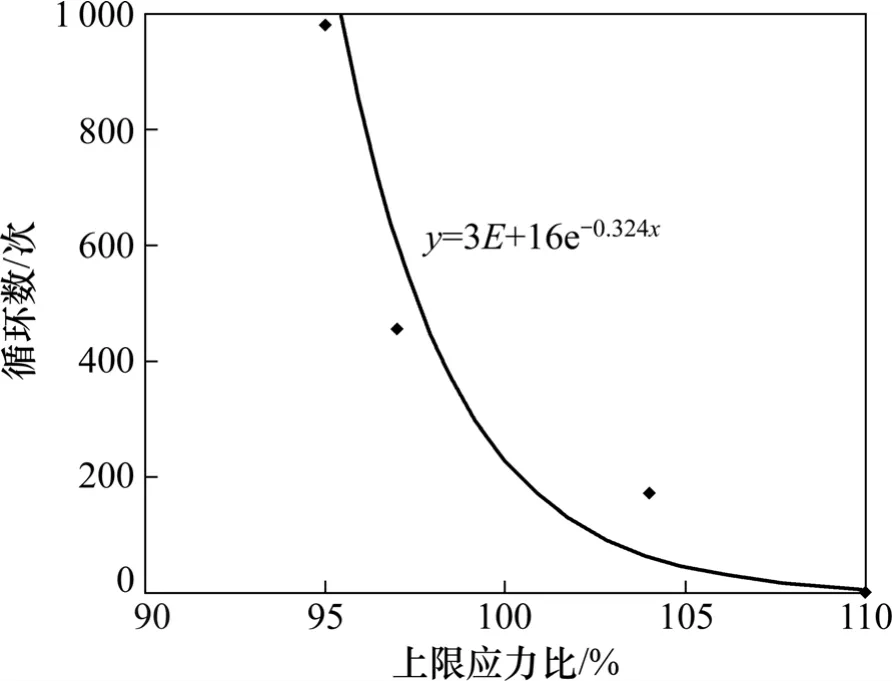
图8 循环扰动下加载上限应力比与循环数的关系曲线Fig.8 Relationship between cyclic times and maximum load ratio

2.4 循环动力扰动作用下的不可逆变形

根据循环加动力扰动条件下的应力-应变曲线，测定每次动力扰动循环的加载曲线的斜率得其变形模量，测定动力扰动循环的卸载应力点(上限应力)的应变得到轴向变形，将它们与对应的循环扰动数绘制在同一个坐标图，得到轴向应变、变形模量和循环数关系曲线。图9 所示为取试件编号为DH-6 作为本次试验具有代表性试件曲线。由图9 可见：轴向变形可以划分为3 个阶段：开始阶段曲线上凸，大理岩在几个扰动下发生较大的应变；然后大理岩进入等速发展阶段，轴向应变以恒定速率呈线性规律发展，应变缓慢增大；最后轴向应变进入加速阶段，曲线快速向上发展，轴向应变迅速增大，在很少的几个扰动下轴向应变迅速增加到极限应变。试样在第1 和第3 阶段的轴向应变增加很快，而且累积轴向应变占总应变的90%以上。第2 阶段轴向应变发展很慢，而且累积变形量仅占总变形的10%左右，但这一阶段占了循环加卸载的绝大部分时间。大理岩的不可逆变形是3 个阶段应变累积的结果，第2 阶段是大理岩承受循环扰动的主要阶段。由图9 可见：弹性模量随循环扰动数的变化也相应的呈3 个阶段，初始阶段，大理岩变形模量急速上升，这主要是大理岩在静载未闭合的微裂在循环扰动下闭合，岩石刚度变大；第2 阶段，大理岩变形模量随循环扰动数缓慢降低，这时的岩石处于密实状态，裂纹逐渐萌生，并稳定扩展。最后阶段，变形模量很快变小，此时大理岩裂纹已经基本贯通，大理岩已经失去承载能力，在很小的扰动下很快产生很大的变形。比较变形模量和轴向应变与循环扰动数关系曲线可见，轴向应变与变形模量的变化阶段是对应的。

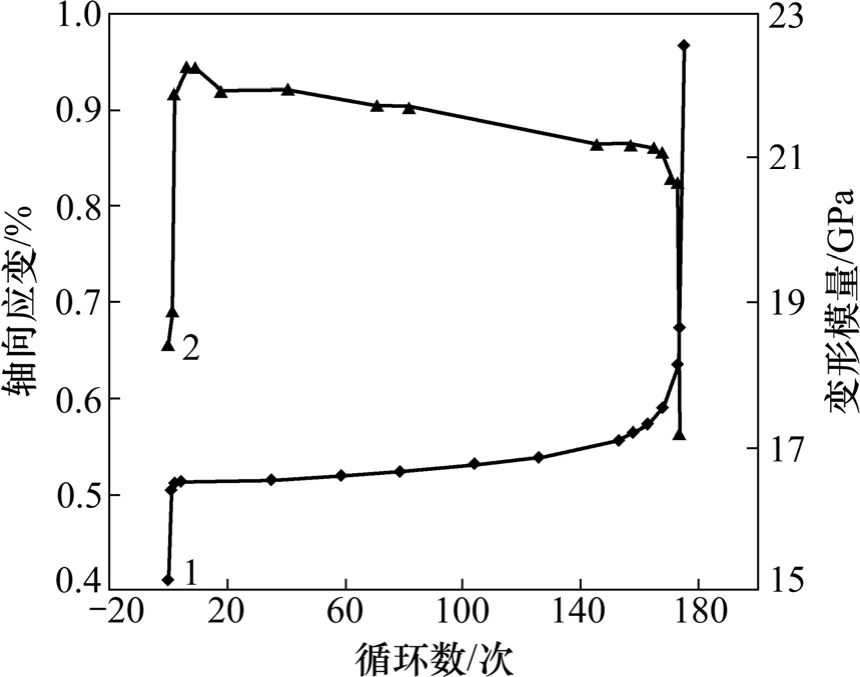
图9 轴向应变、变形模量与循环数关系曲线(试件DH-6)Fig.9 Evolution curve of axial strain and deformation moduli vs cyclic numbers (specimen DH-6)

式中：σ，ε 和E 分别为岩石试件受到的应力、应变和弹性模量；D 为损伤变量，D 反映了材料内部的损伤程度，D=0 时，岩石完整无损伤，D=1 时，岩石完全破坏。

如果考虑每次应力循环幅值不变，研究循环动力扰动过程中岩石的累积损伤，则可视式(3)中σ 为循环应力变化幅值，其值为常量，从而分析累积损伤变量D 和累积应变ε 之间的关系。对式(3)两边对ε 求导并整理得：

式中：ε0为循环开始时的轴向应变，此时D=0；εd为循环结束岩石破坏时的轴向应变，此时D=1。对式(4)从D=0 到1，ε 同时从ε0到εd积分得：

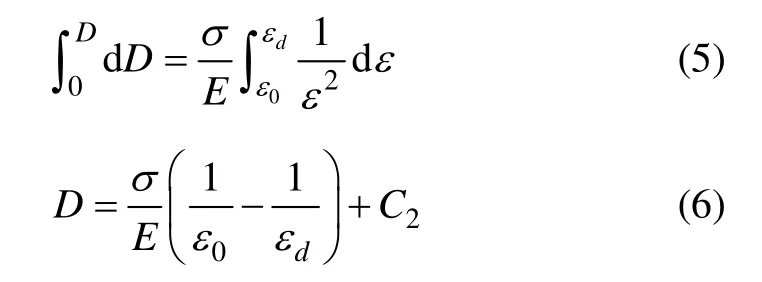
D=0 时，将ε=ε0代入式(6)，得C2=0；将D=1 时，ε=εd代入式(4)

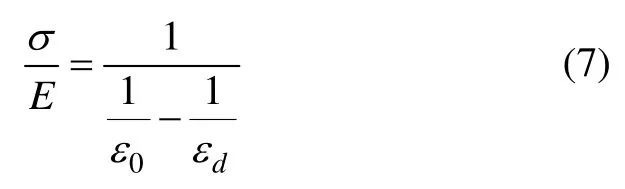
则式(6)变为

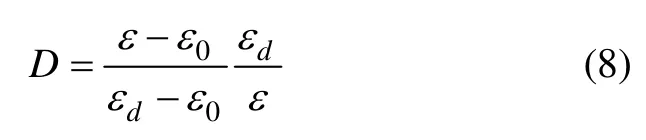
由试验数据测定的动力循环开始时的岩石的轴向应变ε0，循环结束岩石破坏时的岩石轴向应变εd，每次循环扰动的上限应力对应的岩石轴向应变ε，代入式(8)，则可计算每次循环上限应力对应的损伤变量，即本次循环动力扰动后岩石的累积损伤量D。图10所示为由平均应力为60 MPa，动力循环幅值分别为30，35 和 50 MPa 的3 组循环动力扰动试验数据(其中的典型试件的试验数据)按式(8)计算结果绘制的损伤变量与循环数关系曲线。由图10 可见：岩石损伤变量随循环数的增加初期突然增加、之后缓慢增加、最后快速增大导致岩石最终破坏等3 个发展阶段。由图10还可发现，增大循环荷载应力幅值岩石在第2 阶段的循环数明显减少，应力幅值为50 MPa 时第2 阶段基本没有；同时，增大应力幅值还会提高第2 阶段的损伤变量的发展速率，当应力幅值分别为30，35 和50 MPa 时对应的变化率分别为2×10-4，7×10-4和2.5×10-1，这就显著加快岩石疲劳破坏的速度，大大降低了岩石寿命，尤其在应力幅值为50 MPa 时，岩石3 个循环荷载作用下就发生破坏。研究结果表明，不同动力扰动应力幅值对岩石损伤的发展速率和发展阶段具有明显影响。

2.5 岩石循环加卸载破坏形态分析

在静力单调加载和受到静力加循环动力扰动荷载作用下，岩体试件总体上呈单斜面剪切破坏，如图11所示。但是，在静力单调加载作用下，试件产生的剪切面破裂面相对连续、平直和光滑；而在循环动力扰动荷载作用下，岩件产生的破裂面的形态相对复杂，并且存在大量平行于轴向的裂纹和破坏面，岩石膨胀更明显，岩石局部呈碎裂化破坏，临近破坏时会有片落现象，片落的裂块中含有许多磨碎的大理岩晶粒。仔细观察发现，这些纵向张拉裂隙的发育是随动力扰动的循环数的增加而逐渐加深的；循环动力扰动的上限应力大于岩石静力强度的条件下，纵向裂隙对岩石试件的破坏更加明显。动力扰动的循环幅值越大，这些纵向张拉裂隙越发育，这是循环荷载的反复作用和裂纹形成后裂块间不断摩擦造成的。由图11 可见：静力加循环动力扰动作用条件下，大理岩的破坏表现出剪切和张拉疲劳2 种特征。这种剪切和循环的张拉疲劳作用可能导致岩石碎裂化，并在部分试件的试验过程中产生岩石碎片弹射，这可以很好解释冬瓜山铜矿巷道围岩的碎裂化现象和局部的应变型岩爆。

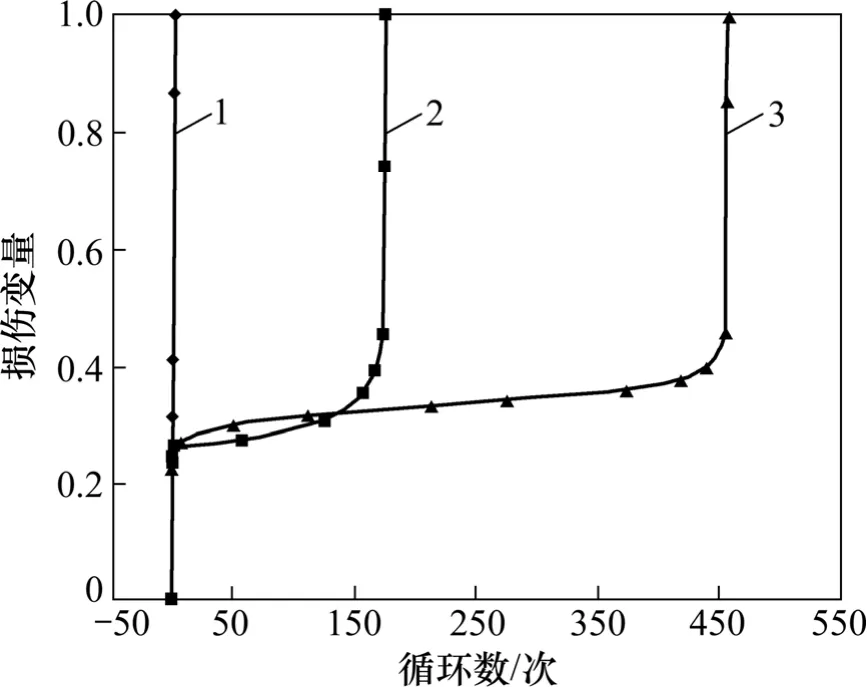
图10 损伤变量-循环数关系Fig.10 Damage variable versus cyclic numbers

图11 不同动载幅值下岩石试件的破坏形态Fig.11 Failure modes of marble specimens under different amplitudes

3 结论

1) 循环动力扰动荷载上限应力达到门槛值之前，大理岩的弹性模量随平均应力增大而增大，动力扰动对岩石抵抗变形的能力起到了强化作用。

2) 当上限应力与岩石静力强度相近时，随着平均应力的提高，每次循环动力扰动周期内岩石的变形量增大；平均应力和循环应力幅值的改变对岩石的疲劳寿命具有明显影响，它们与破坏时的循环数之间呈负指数关系。

3) 随循环数的增加，不可逆变形和损伤变量均呈现先快速增大、然后低速增加，最后高速增长直至岩石破坏的变化规律；变形模量则呈先急剧增大、然后缓慢减小，最后急剧减小的变化规律。不同动力扰动应力幅值对岩石损伤的发展速率和发展阶段具有明显影响。

4) 在静力和循环动力扰动共同作用条件下，大理岩试件产生单斜剪切破裂面和许多次级纵向张拉破裂面，张拉破裂面随动力循环数的增加而增多，试件破坏表现出剪切和张拉疲劳2 种特征。

[1] 李夕兵, 李地元, 郭雷, 等. 动力扰动下深部高应力矿柱力学响应研究[J]. 岩石力学与工程学报, 2007, 26(5): 922-928.LI Xibing, LI Diyuan, GUO Lei, et al. Study on mechanical response of highly-stressed pillars in deep mining under dynamic disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 922-928.

[2] 唐礼忠, 周建雄, 张君, 等. 动力扰动下深部采空区围岩力学响应及充填作用效果[J]. 成都理工大学学报(自然科学版),2012, 39(6): 623-628.TANG Lizhong, ZHOU Jianxiong, ZHANG Jun, et al.Mechanical response of deep stopped-out areas and filling effect under dynamic disturbance[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2012, 39(6):623-628.

[3] 陆菜平, 窦林名, 曹安业, 等. 深部高应力集中区域矿震活动规律研究[J]. 岩石力学与工程学报, 2008, 27(11): 2303-2308.LU Caiping, DOU Linming, CAO Anye, et al. Research on micro seismic activity rules in deep high-stress concentration district[J]. Chinese Journal of Rock Mechanics and Engineering,2008, 27(11): 2303-2308.

[4] 葛修润. 周期荷载作用下岩石大型三轴试验的变形和强度特性研究[J]. 岩土力学, 1987(2): 11-18.GE Xiurun. Study on deformation and strength behavior of the large-sized triaxial rock samples under cyclic loading[J]. Rock and Soil Mechanics, 1987(2): 11-18.

[5] 葛修润, 蒋宇, 卢允德, 等. 周期荷载作用下岩石疲劳变形特性试验研究[J]. 岩石力学与工程学报, 2003, 22(10):1581-1585.GE Xiurun, JIANG Yu, LU Yunde, et al. Testing study on fatigue deformation law of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 1581-1585.

[6] 陶振宇, 潘别桐. 岩石力学原理与方法[M]. 武汉: 中国地质大学出版社, 1991: 87-89.TAO Zhenyu, PAN Bietong. Principle and method of rock mechanics[M]. Wuhan: Press of China University of Geology,1991: 87-89.

[7] 许江, 鲜学福, 王鸿, 等. 循环加、卸载条件下岩石类材料变形特性的实验研究[J]. 岩石力学与工程学报, 2006, 25(增1):3040-3045.XU Jiang, XIAN Xuefu, WANG Hong, et al. Experimental study on rock deformation characteristics under cycling loading and unloading conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Supp.1): 3040-3045.

[8] 席道瑛, 刘小燕, 张程远. 由宏观滞回曲线分析岩石的微细观损伤[J]. 岩石力学与工程学报, 2003, 22(2): 182-187.XI Daoying, LIU Xiaoyan, ZHANG Chengyuan. Analysis of micro and meso-damage of rock by macro-hysteresis curve[J].Chinese Journal of Rock Mechanics and Engineering, 2003,22(2): 182-187.

[9] LIU Enlong, HE Siming. Effects of cyclic dynamic loading on the mechanical properties of intact rock samples under confining pressure conditions[J]. Engineering Geology, 2012, 125: 81-91.

[10] 章清叙, 葛修润, 黄铭. 周期荷载作用下红砂岩三轴疲劳变形特性试验研究[J]. 岩石力学与工程学报, 2006, 25(3):473-478.ZHANG Qingxu, GE Xiurun, HUANG Ming, et al. Testing study on fatigue deformation law of red-sandstone under triaxial compression with cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 473-478.

[11] 肖建清, 丁德馨. 常幅循环荷载下岩石的变形特性[J]. 中南大学学报(自然科学版), 2010, 41(2): 685-691.XIAO Jianqing, DING Dexin. Defolrmation characteristics of rock under constant amplitude cyclic loading[J]. Journal of Central South University (Science and Technology), 2010, 41(2):685-691.

[12] 李树春, 许江, 陶云奇, 等. 岩石低周疲劳损伤模型与损伤变量表达方法[J]. 岩土力学, 2009, 30(6): 1611-1615.LI Shuchun, XU Jiang, TAO Yunqi, et al. Low cycle fatigue damage model and damage variable expression of rock[J]. Rock and Soil Mechanics, 2009, 30(6): 1611-615.

[13] 郭印同, 赵克烈, 孙冠华, 等. 周期荷载下盐岩的疲劳变形及损伤特性研究[J]. 岩土力学, 2011, 32(5): 1353-1358.GUO Yingtong, ZHAO Kelie, SUN Guanhua, et al.Experimental study of fatigue deformation and damage characteristics of salt rock under cyclic loading[J]. Rock and Soil Mechanics, 2011, 32(5): 1353-1358.

[14] 左宇军, 李夕兵, 唐春安, 等. 受静载荷的岩石在周期载荷作用下破坏的试验研究[J]. 岩土力学, 2007, 28(5): 927-932.ZUO Yujun, LI Xibing, TANG Chunan, et al. Experimental investigation on failure of statically loaded rock subjected to periodic load[J]. Rock and Soil Mechanics, 2007, 28(5):927-932.

[15] 马春德, 李夕兵, 陈枫, 等. 双向受压岩石在扰动荷载作用下致裂特征研究[J]. 岩石力学与工程学报, 2010, 29(6):1238-1244.MA Chunde, LI Xibin, CHEN Feng, et al. Fracturing behavior study of biaxial compression of rock subjected to dynamic disturbance load[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1238-1244.