非极限状态挡土墙土压力计算

胡俊强 ，陈建功 ，张永兴

(1. 重庆大学 土木工程学院，重庆，400045；2. 重庆大学 山地城镇建设与新技术教育部重点实验室，重庆，400045)

目前，挡土墙土压力计算大多采用朗肯土压力理论和库仑土压力理论，因其计算简单和力学概念明确得到工程界认可及广泛应用[1-2]。在继库仑和朗肯土压力理论之后，对于平移模式下挡土墙土压力计算理论，已有大量的专家学者对处于极限平衡状态的土体的土压力理论进行了研究。虽然这些研究成果可以用于求极限主动土压力或被动土压力，但这些理论大都建立在挡墙后填土达到极限平衡状态的基础上，而正常工作状态下不可能达到极限状态，而是处于静止土压力和主动土压力之间，这一点从已有的土压力监测资料得到证实。目前，土压力常用计算方法主要有极限平衡法和极限分析法。这些方法的研究对象为处于极限平衡状态的土体，没有考虑位移对土压力的影响，即只有当土体的水平位移达到一定值，土体产生剪切破坏，处于极限平衡状态时，此时对应的土压力用上述土压力理论计算是正确的。大量的现场观测和研究表明：墙体位移对挡土墙上土压力分布有很大的影响。Bang[3]认为土体从静止状态到极限主动状态是一个渐变的过程，提出中间主动状态的概念，指出土压力计算应同时考虑墙体变位模式和变位。Nakai[4]利用有限法研究了土压力与墙体变位的关系。Ichihara 等[5]首先提出土体要达到主动状态，土体对挡土墙墙背的摩擦角必须达到最大值。Sherif 等[6-9]通过模型试验发现非极限主动状态土体达到极限状态时，摩擦角必须达到最大值。周应英等[10-11]分别对砂土填料和压实黏性填土在挡土墙平移情况下进行了土压力试验研究，发现墙体位移对挡土墙上土压力分布有很大的影响。龚慈[12]认为结构物受到的土压力应处于静止土压力和主动土压力之间，经典土压力理论不能计算该状态下的主动土压力。徐日庆等[13]针对刚性挡土墙平动模式下考虑位移效应，建立了墙背与填土间外摩擦角和填土内摩擦角与墙体平动位移的关系，并对水平土楔进行了分析研究。黄斌等[14]利用三轴不排水剪切试验类比挡墙后土体侧向变形过程，得到了非极限主动土压力的计算公式。卢坤林等[15-16]采用卸荷应力路径的三轴试验类比墙后土体的侧向变形过程，建立了摩擦角与位移的关系，进而得到了非极限主动土压力的计算公式，改进了水平层分析法，计算任意位移模式的土压力分布。张永兴等[17]结合非极限状态的填土内摩擦角、墙土摩擦角和墙体位移比的关系对垂直挡墙的非极限状态主动土压力的分布进行了研究。在此基础上，本文作者考虑摩擦角发挥值与墙体平动位移关系，利用薄层单元法对倾斜挡土墙进行非极限状态主动土压力的研究，取挡墙后滑动楔体沿平行于填料坡面的水平薄层作为微分单元体，通过作用在水平薄层的力和力矩平衡条件，建立关于一般挡土墙非极限状态主动土压力的基本方程，进一步得到非极限状态时的土侧压力系数、土压力合力和作用点的理论公式，并与试验数据进行对比分析。

1 挡土墙非极限主动土压力求解

由于从挡土墙位移为零的初始静止状态和位移达到一定程度填土达到极限主动状态之间，存在一个过渡状态，本文称为非极限状态，其对应的土压力称为非极限土压力。进行以下假定：(1) 挡土墙后为均匀无黏性土；(2)土体处于非极限状态时，填土中存在“准滑动面”，形成楔形土体，且准滑动面总是通过挡土墙的墙踵。挡土墙模型如图1 所示。

1.1 计算模型

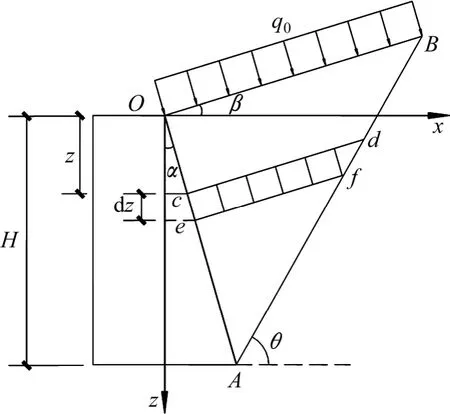
图1 挡土墙模型Fig.1 Model of retaining wall

图2 单元体受力分析Fig.2 Force analysis of element

1.2 平衡方程的建立

对无黏性土，在非极限状态下，可令

其中：mδ 为填土与墙背之间的摩擦角发挥值；mφ 为填土内摩擦角发挥值；Km为非极限状态时土侧压力系数。

由图1 挡土墙模型及图2 微单元体的受力分析模型可得几何参数：

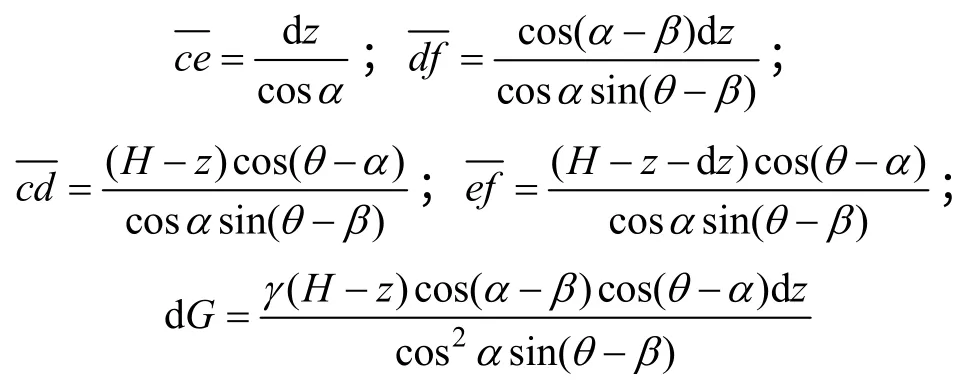
由作用于单元体上的水平方向力的平衡条件：ΣFx=0可得：

将式(1)代入式(3)，并化简得

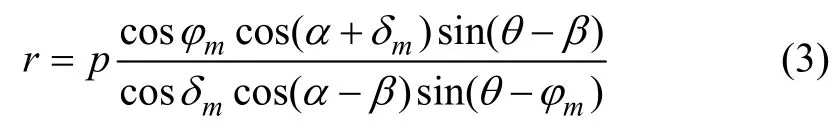
由作用于单元体上的垂直方向力的平衡条件：ΣFz=0，可得

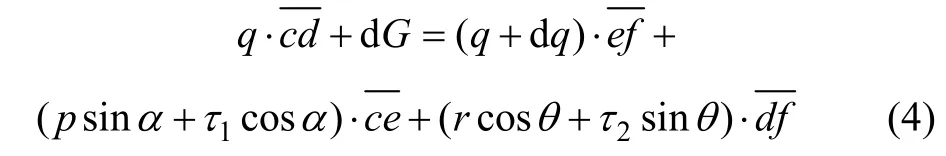
将几何参数及式(1)和(3)代入式(4)，并化简得

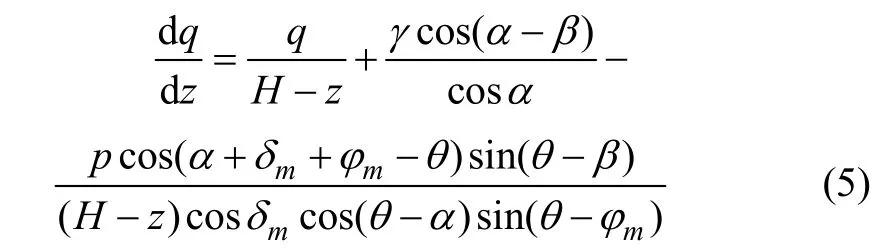
由单元体上的力矩平衡条件：ΣMd=0可得

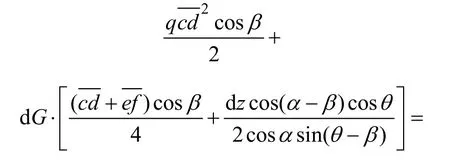
将几何参数代入并化简得

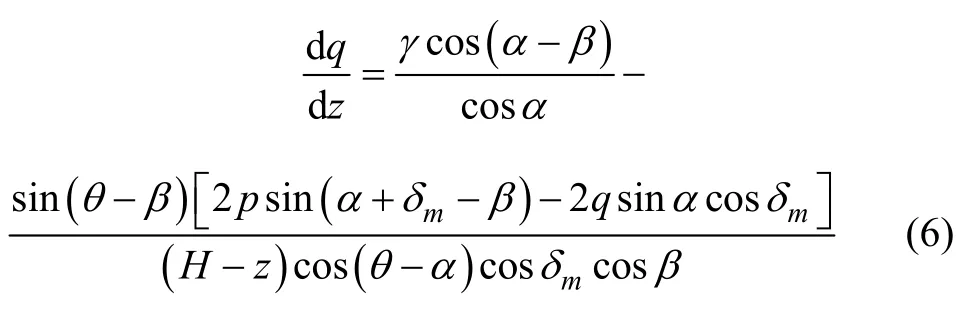
1.3 土压力求解

由式(1)，(5)，(6)得非极限状态土侧压力系数Km：

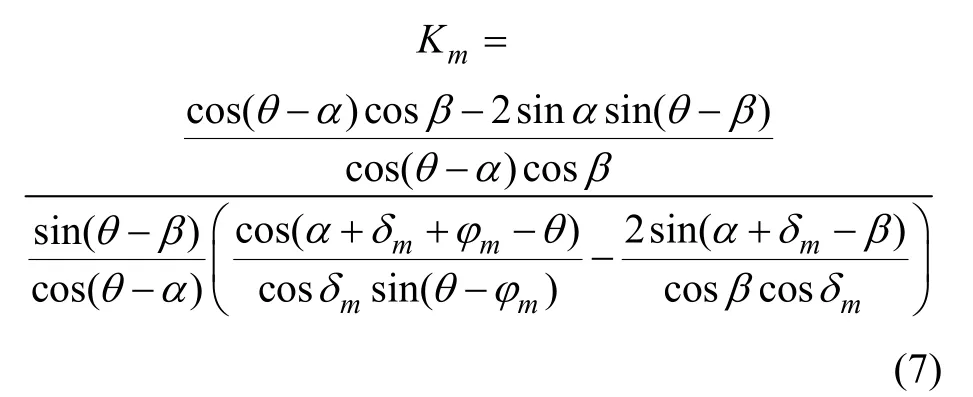
将式(7)代入式(5)得挡土墙非极限状态竖向应力q关于z 的微分方程：

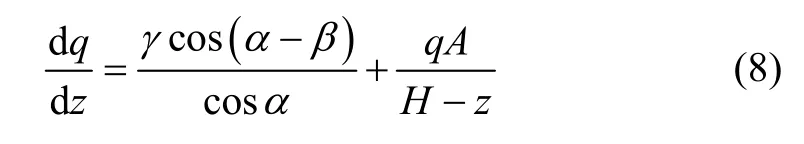
其中：

并解微分方程得

由边界条件z=0，q=q0，得

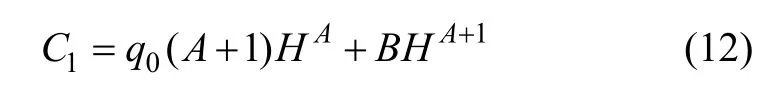
则挡土墙背反力为

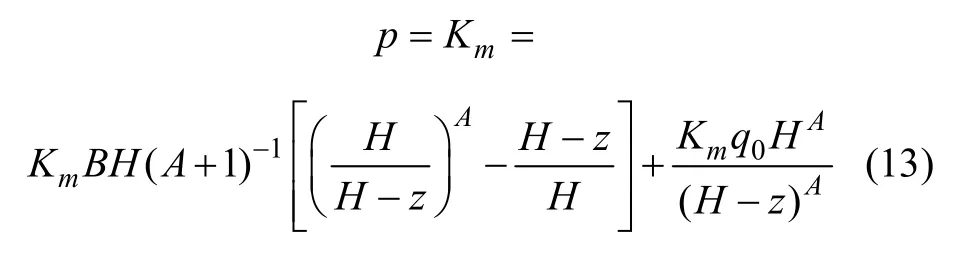
非极限主动土压力合力为

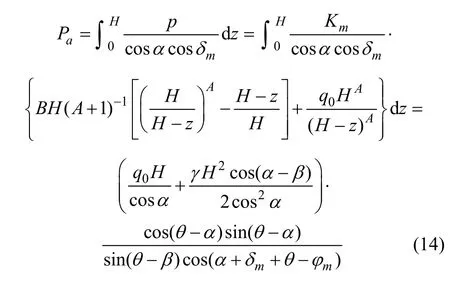
很明显，当α ，β ，mφ 和mδ 已知时，pa是关于θ 的一元函数，为求pa，利用微分求极值的条件：d Pa/dθ = 0，可得Pa取最大值对应θacr：

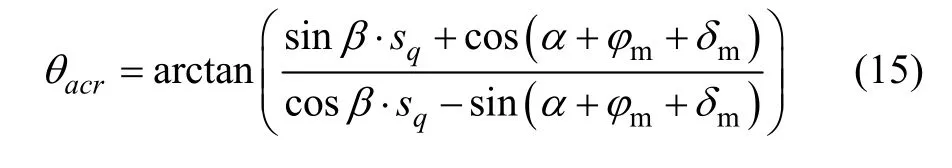
由于土压力合力作用点位置，经计算为

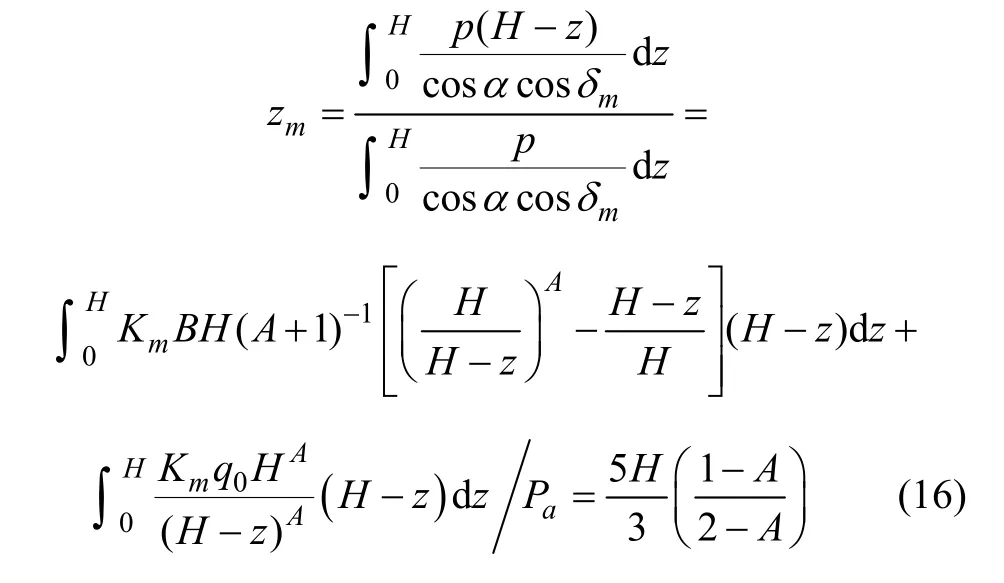
2 φm 和δm 的探讨

要计算非极限状态时挡土墙上土压力，必须确定上述公式α ，β ，q0，mφ 和mδ ，而α ，β 和q0一般可以直接得到，本文主要探讨mφ 和mδ 的取值。目前常用的土压力分析方法通常假定填土与墙背间外摩擦角保持不变。龚慈[12]认为：mδ 一般先于mφ 达到最大值，但为了简化计算，假定二者同时达到最大值，且二者变化趋势相同，并根据前人试验结果拟合并建立了填土内摩擦角mφ 与η 的关系：

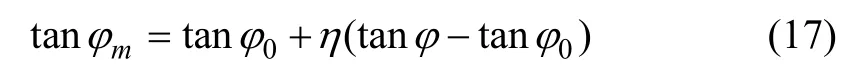
根据假设，墙土摩擦角mδ 与η 的关系为

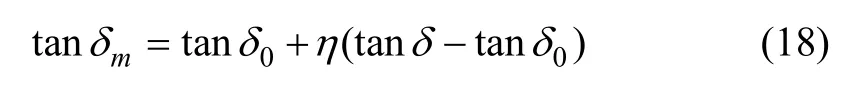
卢坤林等[15]利用卸荷应力路径的三轴试验类比墙后土体的侧向变形过程，建立了填土内摩擦角mφ 与η 的关系：

式中：η =S / Sa；η 为挡土墙位移比；S 为挡土墙(平动)位移；Sa为达到极限状态时的挡土墙(平动)位移；Rf为破坏比。当S=0 时，η=0，土体处于静止状态，此时，φm=φ0，δm=δ0，φ0和 δ0分别为初始状态时填土的内摩擦角和墙土摩擦角。当0＜η ＜1，填土内摩擦角 φm、墙土摩擦角 δm随挡土墙位移比η 的增大而增大；当η=1 时，挡土墙处于极限状态，此时，φm=φ，δm=δ，φ 和δ 分别为极限主动状态时填土的内摩擦角和墙土摩擦角。

对于墙土摩擦角发挥值 δm的取值，国内外学者已经进行了相关研究：Matsuzawa 等[9]建议采用墙土摩擦角δ=2φ /3。龚慈[12]为墙土初始摩擦角 δ0的确定需要结合工程实际，与结构特点、施工工艺、墙背平整度有关。考虑土体初始应力条件，对于埋置式挡土墙，δ0=0；对于墙后分层填土的挡土墙， δ0＞0；若没有给出确切的值，则一般取 δ0=φ/2。

土体初始内摩擦角0φ 为静止状态时土体的内摩擦角，对于正常固结土体，若不考虑初始状态时墙土摩擦角0δ 的影响，则

式中：K0为静止侧土压力系数， K0= 1 -sin φ′，φ′为土体有效内摩擦角。

当墙后砂性填土的初始密度大于其自重压实密度时，且墙后填土分层压实，此时0δ ＞0，需考虑0δ 的影响，此时的0φ 可由改进的库仑方程式[18]求解：

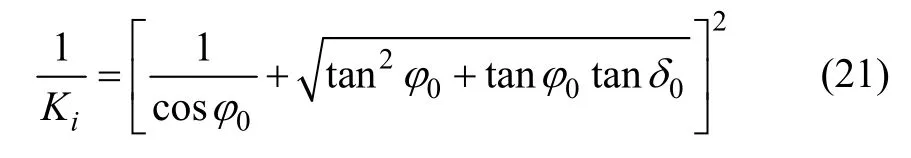
式中：Ki为初始状态时的静止土压力系数。

卢坤林[15]建议某一位移下的墙土摩擦角为δm= (0 -2)φm/3。张永兴等[17]认为非极限状态下挡土墙的 φm和 δm主要与挡土墙的极限状态时的φ 和挡土墙位移比η 有关。

综上所述，挡土墙土体内摩擦角发挥值mφ 和墙土摩擦角发挥值mδ 主要与挡土墙的极限状态时填土的内摩擦角φ 和挡土墙位移比η 有关，其余参数如极限状态时墙土摩擦角δ 、填土初始内摩擦角0φ 、墙土初始摩擦角0δ 均是关于两者的函数。

3 φ 和η 对挡土墙土压力的影响

非极限状态土侧压力系数、土压力合力、土压力合力作用点主要取决于墙土的几何参数α ，β 和q0以及强度参数mφ 和mδ 。而强度参数mφ 和mδ 主要与挡土墙的极限状态时填土的内摩擦角φ 和挡土墙位移比η 有关，因此，挡土墙主动土压力主要由α ，β ，q0，φ 和η 来确定。由于本文研究重点在于考虑墙体位移的非极限状态主动土压力，在墙体移动过程中，只有填土强度参数随着挡墙位移变化，而墙土几何参数α ，β 和q0在挡墙整个移动过程中却始终保持不变。因此，本节仅讨论φ 和η 对非极限状态土压力的影响，几何参数对主动土压力的影响分析与强度参数影响分析相同。在下面的讨论中，令α =0，β =0 和q0=0，即仅考虑墙面垂直，填料坡面水平的挡土墙，取δ=2φ /3，并结合式(17)和(18)进行分析。

3.1 对滑裂面倾角的影响

挡土墙非极限状态滑裂面倾角 θacr随填土内摩擦角φ 和挡土墙位移比η 的变化曲面如图3 所示。可见，对于挡土墙非极限状态滑裂面倾角 θacr随φ 和η 的增大而增大。当η=0 时，此处给出的破裂角 θacr为挡土墙静止状态滑裂面倾角 θa′cr，当η=1 时，此处给出的破裂角 θacr与按库仑理论计算的滑裂面倾角 θa′cr相等。分析可知，非极限状态滑裂面倾角 θacr介于库仑理论滑裂面倾角和静止状态滑裂面倾角之间，且 θa′cr≤ θacr≤ θa′cr，这与文献[7]中的模型试验观测结果相符。

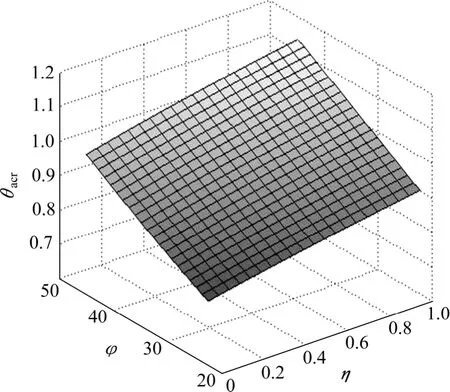
图3 非极限状态滑裂面倾角θacr 随φ，η 的变化曲面Fig.3 Relation surface between θacr and φ，η

3.2 对土压力侧压力系数的影响

非极限状态主动土压力侧压力系数Km随填土内摩擦角φ 和挡土墙位移比η 的变化曲面如图4 所示。由图4 可知，Km随φ 和η 增大而减小。当η=0 时，由式(7)得挡土墙静止状态土侧压力系数K0，当η=1 时，由式(7)得极限状态土侧压力系数K′。经分析可知，非极限状态土侧压力系数Km介于极限状态侧压力系数K′和静止状态侧压力系数K0之间，且K′≤Km≤K0。

3.3 对土压力分布的影响

分析可知，填土摩擦角φ 和挡土墙位移比η 对土压力分布有很大影响。由式(13)和式(14)可知：计算土压力分布形式并不是线性的，式(17)和式(18)表明：本文计算结果对应于挡土墙从静止到极限平衡的整个过程。为了对非极限状态主动土压力随φ 和η 的变化规律进行研究，令H=4.0 m，δ=2φ /3， γ =18 kN/m3，得出一组非极限状态主动土压力Pa随φ 和η 的变化曲面，如图5 和图6 所示。可见：非极限状态主动土压力分布为凸曲线，在η=0.5 时，土压力分布主要集中在挡土墙墙底，随着φ 的增大，土压力强度p 最大值逐渐减小，最大值位置向墙顶方向移动，且土压力强度p 随之逐渐减小。

图4 Km 随φ 和η 的变化Fig.4 Relationship surface between Km and φ, η

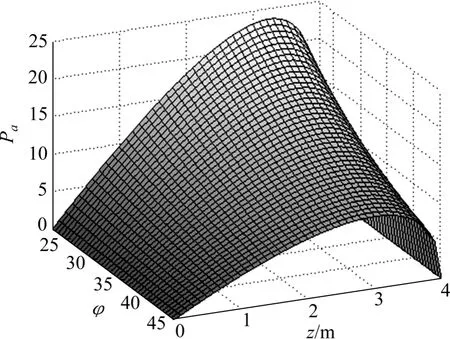
图5 η 不变时不同φ 的主动土压力分布Fig.5 Distribution of earth pressure with different φ and same η

图6 φ 不变时不同η 的主动土压力分布Fig.6 Distribution of earth pressure with different η and same φ

由图6 可知，在φ=34°时，土压力分布主要集中在挡土墙墙底，随着挡土墙位移比η 的增大，土压力强度p 最大值逐渐减小，最大值位置向墙顶方向移动，且土压力强度p 随之逐渐减小。从图5 和图6 可以看出：φ 和η 的变化对土压力的大小和分布影响显著，这与已有文献[7]中的试验观测结果相符。

3.4 对土压力合力作用点的影响

合力作用点距挡墙底的高度zm随填土内摩擦角φ 和挡土墙位移比η 的变化曲面如图7 所示。由图7可知：zm随φ 和η 的增大而增大；非极限状态主动土压力合力作用点高度都在墙高的1/3 以上，作用点高度大致介于挡土墙高度的1/3～1/2 之间，这与文献[7]中模型试验结果相符，但与按极限状态库仑主动土压力理论认为无黏性填土主动土压力合力作用点距墙底的距离等于墙高的1/3 处不同。

图7 zm 随φ，η 的变化Fig.7 Relationship between height of action line of resultant earth pressure and φ, η

3.5 对挡土墙倾覆力矩的影响

对挡土墙墙底取矩，则挡土墙倾覆力矩T 为

则由式(14)和(16)代入式(21)即可得挡墙非极限状态倾覆力矩T。

挡土墙主动状态倾覆力矩T 随填土内摩擦角φ 和挡土墙位移比η 的曲面如图8 所示。可见：倾覆力矩T 随墙后土体内摩擦角φ 和挡土墙位移比η 的增大而减小，因此，增大土体内摩擦角φ 或者δ 都可以增加墙体的稳定性。当η=1 时，此时的倾覆力矩为极限状态的倾覆力矩TA；当η=0 时，此时的倾覆力矩为挡土墙静止状态倾覆力矩T0。经分析可知，非极限状态倾覆力矩Ta介于极限状态倾覆力矩和静止状态倾覆力矩之间，且TA≤Ta≤T0，即静止状态倾覆力矩为主动状态最大倾覆力矩，极限状态倾覆力矩为主动状态最小倾覆力矩。则采用极限状态的倾覆力矩计算平动模式下刚性挡土墙主动非极限状态时的倾覆力矩偏于危险，这与对合力作用点影响分析结果一致。

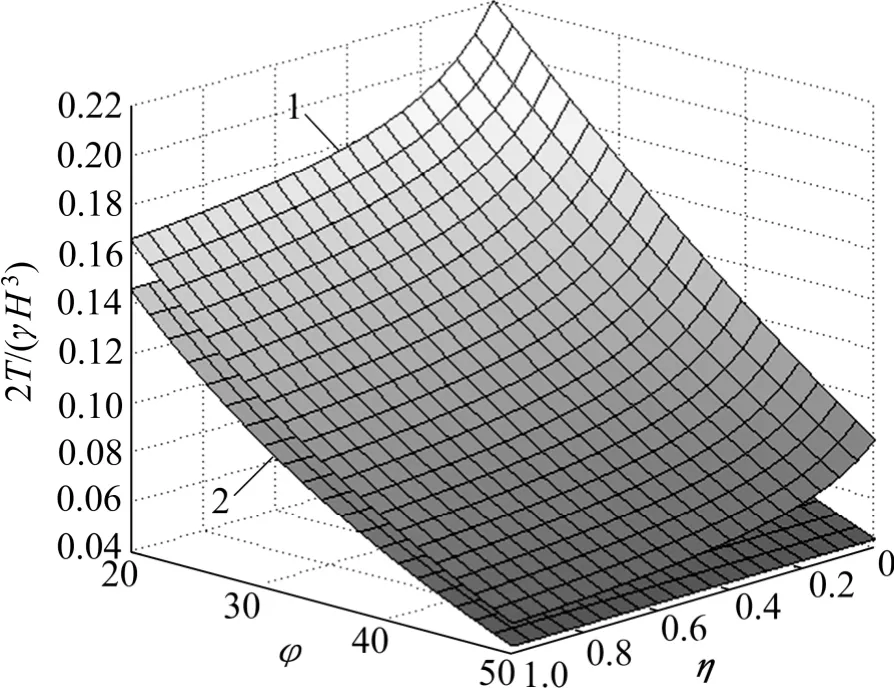
图8 主动状态倾覆力矩T 随φ 和η 的变化曲面Fig.8 Relation surface between T and φ, η

4 实例分析

Fang 等[7]对填土为海砂的刚性挡土墙，对背离填土平动情况进行了一系列模型试验。试验参数为：填土重度γ= 15.4 kN/m3，填土内摩擦角 =φ 34°，挡墙高H=1 m。本文分析进行计算分析时，取墙土摩擦角δ=2φ/3=22.67°，墙土初始摩擦角 δ0=17°，并通过计算可得填土内摩擦角初始值 φ0=8.6°。位移比η 分别取0.05，0.20，0.75 和1.00。由本文推导公式计算挡土墙非极限状态主动土压力分布如图9 所示，将土压力计算值与文献[7]模型试验的实测值进行比较分析。

从图9 可以看出，本文计算的土压力分析结果与实测值的变化规律基本一致，计算结果均与实测结果整体上吻合较好；挡土墙主动土压力随着η 的增大而逐渐变小，且其最大值逐渐向墙底移动，挡土墙主动土压力作用中心和土压力最大值计算值与试验值吻合较好，土压力最大值作用点高度位于距墙底1/3 墙高范围内。另外，由于挡土墙底部受到摩阻力和初始静止土压力的影响，在挡土墙位移较小时，实测值与计算值存在一定的差值。

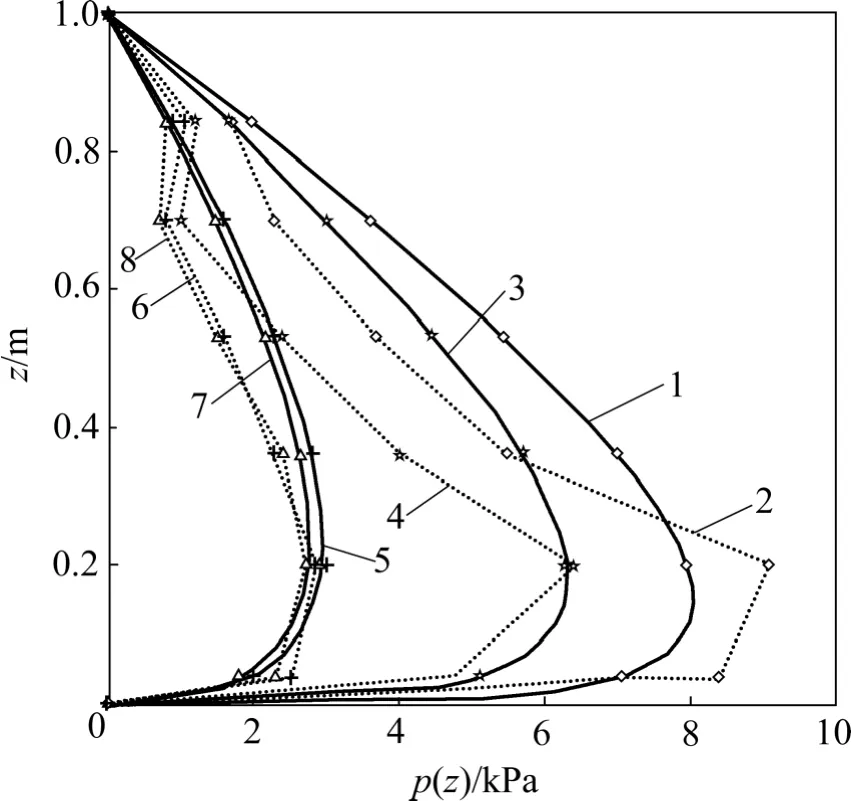
图9 主动土压力计算值与实测值Fig.9 Computed and measured results of case

5 结论

(1) 利用单元体的水平力、竖向力平衡和力矩平衡条件，得到了挡土墙非极限状态土侧压力系数、土压力合力、土压力合力作用点的一般表达式。这些值主要取决于墙土参数α ，β ，q0，φ 和η。

(2) 非极限状态主动土压力侧压力系数Km随φ 和η 增大而减小，且K′≤Km≤K0；非极限状态主动土压力分布为凸曲线，随着φ 的增大，p 最大值逐渐减小，随着挡土墙位移比η 的增大，水平土压力强度p 最大值逐渐减小，φ 和η 的变化对土压力的影响显著。

(3) 挡土墙非极限状态滑裂面倾角 θacr和土压力合力作用点高度zm均随φ 和η 的增大而增大，倾覆力矩T 随墙后土体内摩擦角φ 和挡土墙位移比η 的增大而减小；采用极限平衡理论计算平动模式下刚性挡土墙非极限状态时的抗倾覆稳定性偏于危险。

(4) 采用本文计算方法得到的挡土墙土压力分布与实测结果较吻合，表明本文方法具有理论意义和工程实用价值。

[1] Das B M. Principles of foundation engineering[M]. 7th ed.Singapore: International Thomson Publishing Asia, 2010.

[2] 孙文怀, 裴成玉, 邵旭. 圆形基坑地下连续墙支护结构监测分析[J]. 施工技术, 2006, 36(11): 15-17.SUN Wenhuai, PEI Chengyu, SHAO Xu. Analysis of circular foundation pit diaphragm wall support structure monitoring results[J]. Construction Technology, 2006, 36(11): 15-17.

[3] Bang S. Active earth pressure behind retaining walls[J]. Journal of Geotechnical Engineering, 1984, 14(3): 407-412.

[4] Nakai T. Finite element computations for active and passive earth pressure problems of retaining wall[J]. Soils and Foundations, 1985, 25(3): 98-112.

[5] Ichihara M, Matsuzawa H. Earth pressure during earthquake[J].Soils and Foundations. Japanese Society of Soil Mechanics and Foundation Engineering, 1973, 13(4): 75-86.

[6] Sherif M A, Ishibashi I, L Ee C D. Earth pressures against rigid retaining walls[J]. Journal of Geotechnical Engineering, 1982,108(5): 679-695.

[7] Fang Y S, Ishibashi I. Static earth pressures with various wall movements[J]. Journal of Geotechnical Engineering, 1986, 16(3):317-333.

[8] Fang Y S, Cheng F P, Chen R C, et al. Earth pressures under general wall movements[J]. Journal of Geotechnical Engineering,1993, 24(2): 113-131.

[9] Matsuzawa H, Hazarika H. Analyses of active earth pressure against rigid retaining wall subjected to different modes of movement[J]. Soils and Foundation, 1996, 36(3): 51-65.

[10] 周应英, 任美龙. 刚性挡土墙主动土压力的试验研究[J]. 岩土工程学报, 1990, 12(2): 19-26.ZHOU Yingying, REN Meilong. An experimental study on active earth pressure behind rigid retaining wall[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(2): 19-26.

[11] 岳祖润, 彭胤宗, 张师德. 压实粘性填土挡土墙土压力离心模型试验[J]. 岩土工程学报, 1992, 14(6): 90-96.YUE Zurun, PENG Yinzong, ZHANG Shide. Centrifuge model tests on lateral pressure on walls retaining compacted clayed backfill[J]. Chinese Journal of Geotechnical Engineering, 1992,14(6): 90-96.

[12] 龚慈. 不同位移模式下刚性挡土墙土压力计算方法研究[D].杭州: 浙江大学建筑工程学院, 2005: 10-25.GONG Ci. Earth pressure against rigid retaining wall of different movement modes[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2005: 10-25.

[13] 徐日庆, 龚慈, 魏纲, 等. 考虑平动位移效应的刚性挡土墙土压力理论[J]. 浙江大学学报(工学版), 2005, 39: 119-122.XU Riqing, GONG Ci, WEI Gang, et al. Theory of earth pressure against rigid retaining walls considering translational movement effect[J]. Journal of Zhejiang University (Engineering Science), 2005, 39: 119-122.

[14] 黄斌, 杨洪, 何晓民. 非极限状态主动土压力的研究[J]. 长江科学院院报, 2007, 24(4): 46-49.HUANG Bin, YANG Hong, HE Xiaoming. Research on active earth pressure under non-limit state[J]. Journal of Yangtze River Scientific Research Institute, 2007, 24(4): 46-49.

[15] 卢坤林, 杨扬. 非极限土压力计算方法初探[J]. 岩土力学,2010, 31(2): 615-619.LU Kunlin, YANG Yang. Preliminary study of active earth pressure under nonlimit state[J]. Rock and Soil Mechanics, 2010,31(2): 615-619.

[16] 卢坤林, 朱大勇, 杨扬. 任意位移模式刚性挡土墙土压力研究[J]. 岩土力学, 2011, 32(增1): 370-375.LU Kunlin, ZHU Dayong, YANG Yang. Study of earth pressure against rigid retaining wall with arbitrary displacement modes[J].Rock and Soil Mechanics, 2011, 32(S1): 370-375.

[17] 张永兴, 陈林. 挡土墙非极限状态主动土压力分布[J]. 土木工程学报, 2011, 44(4): 112-119.ZHANG Yongxing, CHEN Lin. Active earth pressure on retaining wall under non-limit state[J]. China Civil Engineering Journal, 2011, 44(4): 112-119.

[18] Chang M F. Lateral earth pressure behind rotating walls[J].Canadian Geotechnical Journal, 1997, 34(2): 498-509.