风洞模型-支撑系统涡激振动测量与分析
2014-03-30王元兴余永生
朱 博,王元兴,余永生
(中国空气动力研究与发展中心 设备设计及测试技术研究所,四川 绵阳 621000)
0 引 言
风洞模型及其支撑系统是风洞试验中实现飞机模型姿态角变化的运动机构,通常采用长悬臂支杆结构,以降低其对流场的扰流干扰,并提供良好的动态试验特性。但是这样的结构通常是多自由度、低阻尼的弹性系统,势必容易产生振动,强烈而持续的振动,不仅会引起运动机构的功能失效,而且还会影响到风洞试验段的流场品质、风洞控制和试验数据的精准度[1-4]。由于引起风洞模型振动的激振力不仅包含机械载荷,还包含了气动载荷,导致振动模态较复杂,减振系统在不同流场速度条件下和不同减振器设计条件下的减振效果以及对试验数据的影响正待研究[5-7],因此,需要从理论上研究模型-支撑系统与试验段气流的流固耦合响应机理,结合支撑系统振动模态试验研究,寻求最佳的减振策略。国内对风洞模型-支撑系统主动减振的研究处于起步阶段,对其振动模态的研究主要采用机械激励的地面试验方法[8]和有限元分析方法[9],对风洞流场中的试验模型涡激振动模态的测量研究很少见。
国内外文献中测量风洞模型振动参数并评估减振器效果的主要方法是在模型上安装加速度传感器[1,8]、应变传感器[2,5]和脉动压力传感器[5,7]等方法。但是在小尺度模型上安装传感器及其信号线的难度较大,这些方法更适用于较大尺寸的试验模型,基于涡激振动是风洞试验模型振动的主要诱因,本文尝试采用热线测量模型尾流涡的方法来分析模型的涡激振动参数及其变化。这种方法不仅适用于小尺度模型的振动测量,同时也为探讨模型涡激振动的机理提供了实验方法。
为了进行对比分析,本文也采用加速度传感器测量模型的振动模态。但是,文献中采用加速度传感器测量模型振动,通常是在时域对加速度信号进行积分获得速度和位移信息,考虑到一般加速度传感器低频特性较差,而且运行的风洞中电磁环境噪声对加速度信号的干扰较大,风洞流场低频脉动较大,导致在时域积分得出的振动速度和位移信号中存在复杂的非线性项,采用去趋势项和时域滤波的方法都难以得到良好的效果[10],每次时域积分都要产生新的趋势项。因此,本文尝试了采用频域滤波和频域积分(FDI)[11]相结合的方法降低上述不利因素的影响。
本文以中国空气动力研究与发展中心的0.55m×0.4m低湍流航空声学风洞尾撑系统为研究对象,在变换风速条件和模型迎角的条件下,测量模型-支撑系统的振动模态,重点对加速度传感器信号采用自功率谱方法获得其主振频率,采用频域滤波和频域积分方法获得其振型,提出并验证基于热线的测量涡激振动的方法。
1 风洞设备及试验系统
1.1风洞设备
本试验在中国空气动力研究与发展中心的低湍流航空声学引导风洞的开口试验段上进行,试验风速范围为25~50m/s。该风洞为回流式低速风洞,配有可更换的开、闭口2种试验段。
1.2模型-支撑振动模态试验系统
模型-支撑振动模态试验系统包括飞机模型、弯刀尾撑系统、振动测量系统和热线测量系统。振动测量系统采用CA-YD107加速度传感器16只,依次沿机翼、机身和模型支杆布置。
针对加速度传感器影响流场环境且不易安装的问题,本文探索采用热线测量模型机翼尾流,进而评估模型振动特性的方法。热线测量系统采用丹麦丹迪公司55P61二维热线,测点布置于机翼后缘2cm处,正对顺气流方向,同时测量X和Y向气流速度。
试验系统传感器布置如图1所示,试验系统实物如图2所示。试验模型迎角分5个状态:0°、5°、10°、15°和20°。试验风速分6个状态:25、30、35、40、45和50m/s。

图1 试验系统传感器布置图

图2 风洞试验系统实物图
2 主要测量和数据处理方法
2.1基于频域滤波和频域积分的结构振型测量
本文采用频域滤波和频域积分(FDI)相结合的方法去除风洞中的干扰信号,该方法先采用频域滤波方法去除干扰信号和趋势项,再进行二次频域积分和傅里叶反变换,获得速度和位移信息,数据处理方法如下:
(1) 首先,对于测量获得的时域离散加速度信号a(n)进行离散傅里叶变换,得到幅值谱X(k),则
(1)
(2)
(2) 其次,对时域加速度信号a(n)在频域进行第m阶振动频率的带通滤波,设模型-支撑系统第m阶固有频率为fm,am(n)为第m阶振动频率的加速度信号,则
(3)
(4)
其中:Δf为频谱的频率分辨率,fw为频域带通滤波器的通频半宽。本文数据采样率为640Hz,采样时间为6.4s,Δf为0.15625Hz,fw取值区间为0~1.09Hz。
(3) 最后,在频域对滤波后的加速度信号进行1次积分,获得速度信号的频谱,进行离散傅里叶反变换即可得到第m阶振动频率的时域速度信号vm(n);在频域对滤波后的加速度信号进行2次积分,获得位移信号的频谱,进行离散傅里叶反变换即可得到第m阶振动频率的时域位移信号dm(n),则
(5)
(6)
ωk=2πkΔf
(7)
2.2基于热线测量模型尾流的振动分析方法
目前测量结构振动的手段主要有加速度传感器测量和激光非接触测量方法。加速度传感器需要安装在模型和支杆上,容易对流场产生干扰,而且在小尺度模型试验件上也难以安装加速度传感器。采用非接触测量方法测量模型振动的方案实现难度较大,难以和压电式振动主动控制系统融合。
为了寻求一种对模型流场环境影响较小,而且可能给振动主动控制系统提供较高频响反馈信号的测量方法,本文基于热线测量模型尾流技术,探索模型尾流与模型振动特性之间的相关性。热线探头布置如图1所示,设置热线测量点位9个,以机翼后缘2cm处为中心0点,沿Y向间隔5mm布置,各点Y向位置坐标在下文中表示为Y+20,Y+15,Y+10,Y+5,Y0,Y-5,Y-10,Y-15,Y-20。采用55P61热线探头测量模型尾流X和Y向速度,并进行二维速度的互功率谱密度分析,互功率谱密度计算方法如下:
设x(n)为热线探头测量获得的模型尾流X向速度,y(n)为热线探头测量获得的模型尾流Y向速度,则X向速度和Y向速度的相关函数为:
(8)
进而,热线探头二维速度的互功率谱密度计算为:
(9)
3 测量结果和分析
3.1模型-支撑系统的振动频率
图3是在模型迎角为0°,风速25m/s时,各加速度测点的自功率谱叠加图,由图可见模型-支撑系统的主导振动有3阶模态,第1阶振动频率为31.1Hz,第2阶振动频率为120.9Hz,第3阶振动频率为221.4Hz。图4是在模型迎角为20°,风速50m/s时,各加速度测点的自功率谱叠加图,可见高阶振动频率略有频移。

图3 模型迎角为0°,风速25m/s时的加速度功率谱叠加图
模型-支撑系统包括具有复杂气动外形的试验模型、低阻尼模型支杆和支撑运行机构等,因此模型-支撑系统的振动特征是以主导频率为主的多阶振动模态。由于模型-支撑系统在不同风速气动载荷下产生一定结构变化,在不同迎角状态下的结构拓扑也有一定变化,导致在不同工况下其高阶振动频率的峰值略有频移。
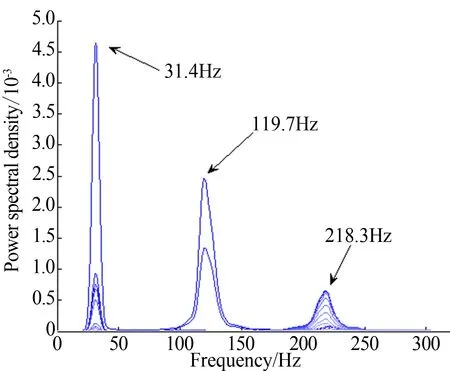
图4 模型迎角为20°,风速50m/s时的加速度功率谱叠加图
3.2模型-支撑系统振型
由于加速度传感器安装在试验模型上(见图2),传感器的结构体和传感线路都对模型的表面流场产生较大干扰。而且相对于小尺度模型,较大的加速度传感器结构体本身在流场中产生的涡激振动不容忽视,其对局部测量结果有影响,加之涡激振动机理较复杂,不利于给出振型图。因此,本文采用振动位移拓扑图来表示支撑系统的振动轮廓。
图5、6和7是在模型迎角为0°,风速25m/s时,采用前述频域滤波和频域积分方法获得的支撑系统3阶振动模态的位移拓扑图,图中的振动位移拓扑线为各测点在同一时刻的位移连线,各位移拓扑线的时间间隔为0.16s。

图5 模型迎角为0°,风速25m/s时的第1阶振动位移拓扑图
由图可见,第1阶振动和第2阶振动的最大幅值发生在机身和机翼,对模型流场扰动最大。第1阶振动幅值最大,有3个振动节点,分别位于8号和9号传感器之间、9号和10号传感器之间以及14号传感器的位置上;若增大频域滤波器的通带带宽至50Hz,则前2个连续出现的节点逐渐相互交错,同时第3个节点位置保持不变,因此,前2个连续节点体现的是第1阶振动在支杆上较长的集中应力区域。第2阶振动是机身和机翼反相的位移振动,有3个振动节点,分别位于1号和2号传感器之间、3号传感器前侧以及14号传感器的位置上。第3阶振动是模型支杆的振动,有2个振动节点,分别位于2号和3号传感器之间以及14号传感器的位置上。节点位置一般是需要加强扭转刚度的系统设计点,最大振幅位置一般是减振控制点[12]。

图6 模型迎角为0°,风速25m/s时的第2阶振动位移拓扑图

图7 模型迎角为0°,风速25m/s时的第3阶振动位移拓扑图
图8是分别在0°和20°迎角状态,不同流场速度下的各阶模态振幅。第1阶模态的振幅远大于其它模态的振幅,因此其振幅曲线特征基本反映了模型的总体振幅曲线特征。由图可见,各阶模态振幅和气流速度、模型迎角正相关,但是第1阶和第2阶模态的振幅线性趋势有一定偏差,第1阶振动幅值在30m/s条件下有交错。然而理论上在20°迎角的时候模型应该已经进入抖振边界[13]。因此,20°迎角的振幅应该明显大于0°迎角的振幅,不应出现大迎角情况下的振幅比小迎角情况下的振幅还要小的反常结果。分析原因,应该是安装于模型表面的加速度传感器对流场的干扰比较大,导致模型的第1阶和第2阶振动幅值趋势有较大的非线性。同时,由于加速度传感器安装在支杆上相对于安装在模型上而言,对流场的干扰要小一些,加速度传感器的安装方式对第3阶振动影响较小,因而第3阶振动幅值趋势线性特征较好。下文的热线测量模型尾流结果可对这一分析进行验证,即第3阶振动是支杆振动,对模型的振幅影响小,因此其振动模态没有在模型尾流中体现。

图8 在不同迎角和流场速度下的各阶模态振幅
3.3模型尾流与模型振动的相关性
图9是在模型迎角为0°,风速25m/s时,模型机翼后缘9个测点的二维速度互功率谱叠加图。由图可见,尾流速度中主要有31和124Hz 2个频率信号,反映了模型振动的第1阶和第2阶模态产生的流场速度脉动。由于第3阶模态主要是模型支杆的振动,因此对流场的干扰不大,机翼的尾流中没有反映出这一频率对应的信号。

图9 模型迎角为0°,风速25m/s时的机翼尾流二维速度互谱叠加图
图10是在模型迎角为5°,风速25m/s时,模型机翼后缘的二维速度互谱叠加图。由图可见,Y+10和Y+15测点处于机翼尾流分离涡中,气流频率成分比较多,无明显峰值频率。Y+10和Y+15以外的其他测点,探头处于机翼尾流分离涡的边缘附近,能够测量分离涡的脱落频率,脱落频率与模型振动频率相对应。
图11是在不同迎角和速度条件下,各测点的X向速度标准偏差的均值统计(Y向统计结果相似)。由图可见,模型尾流气流振幅和气流速度、模型迎角正相关,线性趋势比较明显。这一测试结果与理论分析结果较吻合,即激励模型振动的分离涡产生于来流速度和模型迎角形成的模型上下表面气流压差,较大的模型迎角、来流速度可导致较大的涡流脉动,从而引起模型涡激振动。在迎角为10°以上的条件下,飞机模型进入迎角抖振边界,振动幅值突然大增,因此,尾流的速度脉动量在模型迎角增加到10°时有明显突增。

图10 模型迎角为5°,风速25m/s时的机翼尾流速度互谱叠加图

图11 在不同迎角和流场速度下的模型尾流气流脉动量
4 结 论
本文给出了风洞模型-支撑系统涡激振动模态的测量方法、分析方法和测量结果。
采用基于加速度传感器的功率谱分析方法,获得了模型-支撑系统的三阶振动频率分别为:31.1、120.9和221.4Hz。
采用基于加速度传感器的频域滤波和频域积分方法,提高了有效信号的信噪比,获得了模型-支撑系统振动的振型和振动节点位置,从而为模型-支撑系统扭转刚度设计和流固耦合响应机理分析提供依据。
采用热线测量模型尾流分离涡脱落频率的方法,获得了模型1阶和2阶振动的尾流涡激频率分别为31.1和124.1Hz,并从测量尾流速度脉动量获得了模型振幅变化和抖振边界信息,该方法有利于小尺度的模型振动测量,而且相对于加速度传感器装于模型表面的直接测量方法而言,对试验模型的绕流流场干扰较小,为测量风洞试验模型的涡激振动模态提供了一种方法。
试验数据表明模型振幅和模型迎角、气流速度正相关,模型尾流气流脉动量和模型迎角、气流速度正相关,气流速度脉动量反映了模型振动的幅度,因此,采用测量模型尾流气流脉动量的方法,可以评估风洞模型涡激振动的幅度变化和模型的抖振边界。
虽然热线对模型流场干扰较小,但是,热线难以测量无风载的模型振动频率,而且热线的测量位置对尾流频谱的测量结果影响较大,因此,这一方法还有待更深入研究。
参考文献:
[1]Balakrishna S,Heather Houlden,Butler D H,et al.Development of a wind tunnel active vibration reduction system[R].AIAA 2007-961.
[2]Roger M Glaese,Gregory L Bales,Sean Hsu,et al.Reduction of dynamic response of a wind tunnel sting mount using a hub damper unit[R].AIAA 2010-1307.
[3]王勋年,祝明红,孙传宝,等.低速大迎角尾撑支架干扰试验研究[J].实验流体力学,2007,21(2): 8-12.
Wang Xunnian,Zhu Minghong,Sun Chuanbao,et al.Investigation on the interference of rear sting supports at high angle of attack in low speed wind-tunnel[J].Journal of Experiments in Fluid Mechanics,2007,21(2): 8-12.
[4]梁鉴,张卫国,王勋年,等.4m×3m 风洞无人机模型振动抑制系统研制[J].实验流体力学,2007,21(4): 65-70.
Liang Jian,Zhang Weiguo,Wang Xunnian,et al.Development for restraining oscillation device of the UAV model in the 4m×3m wind tunnel[J].Journal of Experiments in Fluid Mechanics,2007,21(4):65-70.
[5]Balakrishna S,Butler D H,White R,et al.Active damping of
sting vibrations in transonic wind tunnel testing[R].AIAA 2008-840.
[6]Michael J Acheson,Balakrishna1 S.Effects of active sting damping on common research model data quality[R].AIAA 2011-878.
[7]Balakrishnal S,David H Butler.Design and performance of an active sting damper for the NASA common research model[R].AIAA 2011-953.
[8]陈卫东,邵敏强,杨兴华,等.跨声速风洞测力模型主动减振系统的试验研究[J].振动工程学报,2007,20(1): 91-96.
Chen Weidong,Shao Minqiang,Yang Xinghua,et al.Experimental evaluation of an active vibration control system for wind tunnel aerodynamic models[J].Journal of Vibration Engineering,2007,20(1):91-96.
[9]陈万华,王超琪,谢国栋,等.FL_26风洞模型支撑系统动态仿真分析[J].中国机械工程,2012,23(2): 161-166.
Chen Wanhua,Wang Chaoqi,Xie Guodong,et al.Dynamic simulation analysis of model support system in FL-26 wind tunnel[J].China Mechanical ngineering,2012,23(2): 161-166.
[10]顾名坤,吕振华.基于振动加速度测量的振动速度和位移信号识别方法探讨[J].机械科学与技术,2011,30(4): 522-526.
Gu Mingkun,Lyu Zhenhua.Identification of a mechanism's vibration velocity and displacement based on the acceleration measurement[J].Mechanical Science and Technology for Aerospace Engineering,2011,30(4): 522-526.
[11]Hamming R W.Digital filters [M].Englewood Cliffs,NJ: Prentice-Hall,1989.
[12]白冰,常军,刘正兴.梁振动控制中压电作动器的位置优化准则[J].上海交通大学学报,2005,39(2): 288-292.
Bai Bing,Chang Jun,Liu Zhengxing.Optimal placement criterion of the piezoelectric actuators for vibration control of beams[J].Journal of Shanghai Jiaotong University,2005,39(2): 288-292.
[13]孙勇军,卢晓东,刘娟.JL_6飞机抖振边界试飞技术及相关性分析[J].飞行力学,2010,28(2): 85-88.
Sun Yongjun,Lu Xiaodong,Liu Juan.Flight buffet boundary test technique and correlation analysis for JL-6 aircraft[J].Flight Dynamics,2010,28(2): 85-88.
作者简介:

朱博(1973-),男,广西百色人,硕士,高级工程师。研究方向:风洞测试、声学测试、数据采集、信号调理和热线测量技术。通信地址:绵阳市涪城区迎宾路69号404室 (621000)。E-mail:bobjou@139.com
