自由落体下落速度振荡现象的研究

2014-03-30李轶明

实验流体力学 2014年5期

李轶明

(中国石油大学(北京) 石油工程学院,北京 102249)

0 引言

固体在流体中的下落过程是一个经典的流体力学问题，同时在众多工业领域中具有实际应用价值。这一过程是流体与固体之间的受力耦合过程，会产生十分复杂的现象[1-2]，而物体的下落速度是描述问题的关键参数。物体在下落过程中，受到重力和流体阻力的作用，当阻力和重力达到平衡时，降落速度将不会再增加。但这个速度是否稳定则取决于物体形状、运动状态和物理特性、绕流场特性及流体物性等因素，其下落速度并不一定是一个固定值。Joseph和Liu[3]测量了圆柱以不同角度在不同流体中的自由下落过程，记录了圆柱在水平和垂直方向上的运动轨迹，发现圆柱下落的过程与圆柱的尺寸、重量以及流体特性有关。Liu和Nelson等人[4]测量了不同流体中圆球沿倾斜平面的运动规律，实验中发现与粘性流体不同的是在粘弹性流体中圆球出现了异常翻滚现象。Mollinger和Cornelissen等人[5]通过实验研究了非牛顿流体中球形体下落过程中速度的振荡现象，在球体下落过程中，其运动速度会不断减低，但是当速度降低到一定值之后突然增加，这与非牛顿流体的物性参数有关。

本文通过实验和数值模拟的手段研究多种形状的小型刚体在空气中的下落过程，实验模型在对称性上有较大差异，以验证物体对称性对下落速度稳定性的关键作用。实验在立式风洞中进行，基于相对运动原理，物体相对于风洞试验段(即地面)的速度叠加与试验段气流相对(即相反)的速度，即可模拟物体下落时相对地面的速度。例如物体在立式风洞向上的匀速气流中对于试验段处于悬浮(或称悬停)状态，就等同于物体在静止空气中相对于地面以该速度匀速下落的状态；而如果物体对风洞试验段(即地面)存在相对运动，即相当于该物体在静止大气中做变速降落运动。在下述讨论中，本文将依这种相对运动的关系用立式风洞的试验现象来研究物体在近地面的静止大气中自由降落时的速度变化规律。这里强调近地条件，是说明物体的重力加速度不变，空气的密度不变。

1 自由下落物体速度振荡现象实验研究

1.1风洞立式试验段

试验在北京大学湍流与复杂系统国家重点实验室一号边界层风洞立式试验段中进行(见图1)。试验段为直径100mm的有机玻璃圆管，可方便CCD拍摄，出口处装有皮托管，通过差压计测量来流速度[6-7]。为了降低气流湍流度，试验段底部装有阻尼网，同时可防止实验物落入风洞中，在出口处装有隔网防止实验物飞出试验段。风洞风速通过可控硅-交流电机调节，调节范围0～25m/s。

1.2实验模型

为了研究下落物体的下落特征，有针对性地选取了几类典型形状的物体进行实验测量，包括：圆球、立方体、长方体、短圆柱体和圆盘。圆球为乒乓球，直径40mm，重2.7g，最大截面积为1256.6mm2。其余模型由轻质木材做成，模型参数如表1所示。图2是试验模型的照片。

图1 风洞立式试验段

圆球、立方体、长方体、短圆柱体及圆盘

表1模型参数及平均下落速度测量结果

Table1Characterofmodelstesedinthewindtunnel

实验模型模型参数及实验结果准悬浮状态平均风速/(m·s⁃1)几何尺寸体积/mm3质量/g乒乓球8．5直径40mm335102．7立方体7．8边长28．94mm270002．7长方体约7．3边长37．8mm、25mm、37．8mm357213．6短圆柱约6．8直径40mm、高20mm251322．5圆盘约4．0直径43．7mm、高10mm149981．5

1.3物体自由下落实验观察

首先将实验模型置于风洞垂直试验段入口处，然后缓慢提高风速，当达到一定风速后模型将升起进入试验段并出现某种悬浮状态。图3为各实验模型悬浮在试验段中的照片。

从左至右：圆球、立方体、长方体、圆柱体及圆盘

实验观察到的这5种模型的悬浮状态可以分为3类：

第1类，在一定风速下，出现较稳定的悬浮状态。圆球与正方体模型属于这一类，前者中心对称，后者有三个正交的对称轴。在一定风速的气流中，它们能较稳定地悬浮于立式风洞的试验段中。图4显示的是风洞试验段中悬浮的正方体。观察发现，悬浮的圆球和正方体模型会有一些方向和大小都是随机的转动和摆动。但相对来说，球模型转动和摆动的幅度和速度要远小于正方体模型。此外还观察到处于悬浮状态的正方体模型没有出现一个频度占优的方位姿态，也就是说方位姿态是随机的。由此不难想象，一个高空下落的正方物体可能以任一个方位姿态着地。

图4 风洞试验段中悬浮的正方体

第2类，悬浮状态较不稳定。反映在风洞实验过程中是调整风速使模型悬浮比较困难。在某一个风速范围内，模型都会出现悬浮状态，但却维持时间不长就从试验段中消失，或掉到试验段入口，或冲到试验段出口。本次试验中，长方柱模型和短圆柱模型属于这一类。实验观察发现在悬浮状态下，这两种模型自身都在做随机的转动和摆动，其幅度和速度都大于第1类的对称性强的球形和正方形模型。而它们还有一个特点，就是处于悬浮状态时，主要都是处于气动阻力较大而不是较小的方位姿态，如长方体模型的迎风面是面积大的矩形平面，而短圆柱则是圆平面。由此也可以推想，从高空落下的这类形状的物体，以面积大的一面着地的概率较大。

第3类，悬浮状态很不稳定。圆盘模型就是属于这一类。在风洞立式试验段中，在某一范围的风速下，都可能出现圆盘的悬浮状态，但这种状态保持的时间大都很短，如几秒钟，极少情况下也会较长，如10s以上。处于这种悬浮状态时，模型会随机地快速转动和摆动，同时大部分时间是圆盘面处于大迎角而不是小迎角的状态。可以理解为：因为圆盘在小迎角状态是气动不稳定的，即气动力矩会使其迎角增大进入大迎角的随机摆动和转动状态。在自然界中，宽大的落叶是摇摇晃晃飘落下来的而不是以很小的迎角快速砸向地面也是同样的机理。

1.4下落平均速度的测量

在风洞立式试验段中，实验模型进入接近悬浮的状态时，物体受到的重力与阻力基本平衡，此时的风速被认为是模型下落达到比较稳定速度时的平均速度。这个速度可以通过风洞立式试验段出口的皮托管风速计测得，结果如表1所示。实际上，对于对称性好的圆球和正方物体模型，这个速度和它们自由下落的最大速度对应，但对于对称性不好的长方体、短圆柱特别是圆盘，表1的风速只是对应一种可能的悬停风速，因而也是一种可能出现的(不是唯一的)下降的最大风速。

1.5下落瞬时速度的概率分布

为了得到模型下落瞬时速度，详细分析模型悬浮状态出现时间段内的所有图像(每帧图像拍摄时间间隔为1/15s)，通过获取模型中心位置的坐标得到1/15s的平均速度，并近似认为这一速度值是瞬时速度。由于此速度为物体悬浮状态下相对风洞的运动速度，需叠加与风洞气流相对的速度得到物体的实际下落瞬时速度，最终将所有瞬时速度绘成箱式图(见图5)。

图5 瞬时下落速度分布箱式图

图5反映出5种模型下落速度的分布规律，针对每个形状的分布图，上下两点为最大值和最小值，中间的两个长方形上沿代表速度概率分布为95％的速度值，下沿为5％，中间的水平直线代表分布函数的中值，而长方形中间的小正方形代表算数平均值。从瞬时速度值的平均值来看，球形、正方形、长方体、短圆柱体和圆盘的平均下落速度依次降低，这是由各模型的气动外形不同引起的。除了平均下落速度，瞬时速度的概率分布可以更好地反映模型下落过程中的细节信息。从瞬时速度概率分布形式来看，球形和正方形由于其对称性较好，同时在实验中观察到模型出现随机性旋转，其迎风面积和风阻系数等气动参数随时间的变化不大，球形和正方形模型下降速度概率分布函数的范围较窄，最大值和最小值之差也较小。而由于正方形较球形来讲不同姿态下的气动特征稍有不同，这也使其速度概率分布函数上最大与最小值之间的差异较球形稍大。长方体和短圆柱的对称性稍差，不同姿态角下的迎风面积和阻力系数差距很大，从其速度概率分布函数来看，其宽度较对称性较好的球形和正方形有较大增加，说明模型在下落过程中速度的震荡较大，即模型以不同的姿态角和不同的速度下落，速度最大最小值之差可以达到1m/s。对于圆盘，最大最小值之间的差别很大，达到2.5m/s，这主要是由于其对称性较差，圆盘不同姿态时的迎风面积差距较大，可以带来下落速度的较大差别，圆盘下落速度最小值出现在迎风面积最大的姿态，而最大值则出现在圆盘迎角为0的姿态。由其下落速度概率分布函数的特征可知，两种极限状态并不是主要的状态，也就是说圆盘不可能保持以这两种姿态下落，实际下落是介于最大和最小值之间的状态，由之前的实验观察可知，圆盘主要是以快速旋转和摆动的状态下落，并且是大迎角占优，小迎角属于不稳定状态。

2 数值模拟

为了更加详细研究物体在下落过程中的运动行为，采用数值模拟手段对实验结果进行补充研究。主要应用FLUENT软件中的k-ε模型[8-9]求解不可压Navier-Stokes方程组得到速度和压力场分布，对物体下落过程中物体周围的流体流动状态进行研究，同时得到物体在空气中下落姿态特征、运动轨迹及受力情况。为了简化问题，采用二维数值计算，选择正方形作为研究对象，采用了两种数值模拟方法。

第1种模拟方法模拟了固定的正方形模型在不同来流方向时的绕流流场，计算域尺寸2m×2m，正方形尺寸为0.2m×0.2m，位于计算域中心。正方形周围网格划分采用正方形网格，较远处为三角形网格，网格均采用固定网格，计算正方形在不同姿态下受到的力和力矩。取正方形一个边(见图7左上图，最下面的边)的垂直线作为基准，与来流夹角为0°～45°，间隔5°，共10个角度。图7给出了其中4个角度(0、15°、30°及45°)。网格节点数为3000左右。

第2种数值模拟采用了更大的计算域，尺寸为20m×20m，计算中采用了动态网格技术，用于模拟正方形的运动过程。相对较大的计算域使得物体有足够的运动空间，对于下落速度不稳定的情况，可以得到更长时间段内的运动轨迹(因为运动网格技术不能处理物体运动到计算域之外的情况，一旦正方形移动出计算域，计算将停止)。正方形周围的网格划分被加密，可以提高计算精度同时减少远处梯度较小处的计算量，总网格节点数为10000左右。

2.1动态网格技术

如上所述，为了计算正方形的运动过程，采用了动态网格技术[10]，图6为初始状态和计算过程中的网格分布的局部图(t=0、5、10及15s四个时刻)。在初始状态时，正方形位于计算域中心，通过用户自定义文件给出正方形的质量和扭转惯量，正方形在重力、流体压力及粘性应力作用下，发生运动。每隔一个计算时间步长，通过六自由度受力分析可以得到正方形在X方向和Y方向上的速度以及Z方向上的转动角速度。根据速度参数可以得到正方形下一时刻的位置，网格会被自动重新划分，并进行下一步计算。

2.2边界条件及求解过程

计算域入口(底部)为速度边界条件，出口为压力出口边界条件，两侧为无滑移壁面边界条件，正方形模型四边为固壁边界条件。由于作了二维简化，来流风速不能以实验得到的风速作为参考，通过调整入口边界条件，同时监测物体阻力系数和y方向速度的变化，当y方向的加速度接近0时认为正方形在此速度下会进入悬浮状态，由此确定入口速度边界条件的速度大小为20.5m/s。

对于第1种模拟方法，采用定常求解方法，模拟各种姿态下正方形所受的力和扭矩。对于第2种方法，为了模拟正方形在计算域中的运动过程，采用了时间非定常求解方法，计算时间间隔为0.5ms。

图6 动态网格

图8为正方形受到的阻力系数和扭矩系数随角度的变化规律。阻力系数在0°的时候最小，随着角度的增加，阻力系数会随之增加。当角度为45°时，阻力系数达到极值。由于正方形的对称性，超过45°之后的受力情况会以45°为对称轴呈对称分布。当角度为90°时，受力情况与0°相同。

图8同时给出扭矩系数的分布规律，当正方形逆时针旋转一定角度之后(小于45°)，物体扭矩系数为负值，即受到一个使之顺时针旋转的扭矩，扭矩绝对值大小随着角度的增加而增加。当角度达到15°左右时，达到最大值。当角度进一步增加之后，扭矩的绝对值下降，当角度为45°时，扭矩恢复为接近0。超过45°之后，由于正方形的对称性，受到的力矩方向发生变化，绝对值以45°为对称轴呈对称分布，即一旦角度超过45°，正方形将受到一个使之偏转角度增加的力矩。

图7 速度场分布(以最大速度归一处理)

图8 阻力系数及扭矩系数图

2.3运动轨迹及姿态数值模拟

除了不同姿态角下正方形周围流场的计算模拟以外，采用动态网格技术对处于20m×20m计算域中的正方形的运动规律进行了数值模拟研究。正方形的初始位置在计算域中心，初始角度为0°。图9显示了正方形在50s的计算时间段内角度随时间的变化规律。当T=0时，虽然根据稳态计算结果(见图7)正方形的受力为对称受力，受到的扭矩也接近零，即正方形能够保持这个姿态，但是在瞬态流场计算过程中，气流的不稳定性可以使正方形发生微小的角度偏转。

根据前文对扭矩的计算可知，当正方形姿态发生变化后，会受到一个反向的扭矩使之回到初始状态(角度为0的状态)。但是由于惯性的作用，当正方形姿态角为0时，仍然存在一个角速度使之越过角度为0这个姿态，随之受到反向力矩使角速度绝对值降低，直至降为0，这时正方形的姿态角达到极值；而后角速度改变方向，正方形的姿态角再次向角度为0的状态变化。从模拟结果(见图9)可以看出正方形姿态度随时间呈现出上述震荡变化过程，其振幅在10s之内会出现逐渐增加的现象，但是在接下来的过程中这一幅值会稳定在27°～32°之间。

图10为正方形在计算域中的轨迹，图11为计算过程中t=10、15、20和25s 4个时刻流场中的速度分布图，由最大速度25m/s进行归一化处理。正方形的初始姿态为0°，阻力系数最小，这时正方形受到的重力要稍大于阻力，因此存在向下的速度，从图10得到的正方形运动轨迹可以看出这是一个下落过程。随着正方形姿态角的变化，尤其是当达到30°左右时，由于阻力系数的升高，阻力与重力大体平衡，从轨迹图上可以看到Y值的振荡规律，即正方形进入悬浮状态。

图9 正方形姿态角度随时间的变化

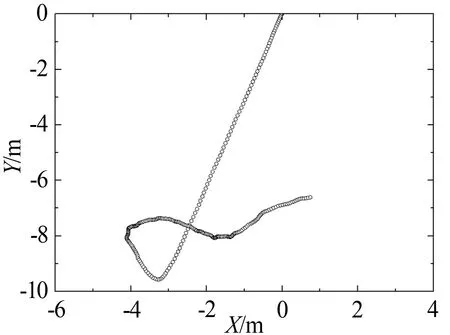
图10 正方形的运动轨迹

图11 速度分布图

3 讨论与结论

利用小型立式风洞对五种典型形体的刚性模型进行了其在上升气流中悬浮特性的实验，主要目的之一是研究物体在近地大气中自由下落达到重力与空气阻力平衡时下降速度的特性。实验观察、测量和分析表明，空间对称性好的物体具有稳定的悬停特性，表明这类物体有稳定的自由下降最大速度；而空间对称性不好的物体，则在上升气流中呈现不稳定的悬停状态，表明这类物体具有不确定的最终下降速度。换言之，从高空(这里假定是几百米的近地高空)落物来看，这类具有不稳定悬停状态的物体的最终落地速度是不确定的。它有一个理论极限值，即始终以最小阻力姿态下落时达到的最大速度。但实际的自由落体运动中这个速度是很难达到的，因为最小阻力的方位姿态多是气动不稳定的，在自由下降的过程中任何扰动都将发散性地改变其空间姿态，增大了阻力，降低了速度。

用小型的立式风洞和小模型做悬浮实验能够定性和某种程度定量地反映不同形体的物体在上升气流中的悬浮特性和由此推断出的自由落体在重力和气动阻力达到平衡时的下降速度特性。但由于风洞截面积和模型截面积之比为6，风洞壁影响了悬浮状态的物体产生的横向运动，此外试验段高度也不够，不能更好地反映悬浮不稳定的运动历程。所以实验的一些定量结果只有参考意义。

二维正方形物体周围流场以及正方形的阻力系数、扭矩和运动轨迹等数值试验结果表明：正方形不存在姿态角不变的平衡位置，在气流小扰动的作用下，正方形发生微小的角度偏转，在与角速度相反的扭矩和惯性共同作用下，正方形物体姿态角出现正负振荡现象，振荡幅值最终稳定在27～32°。

致谢:感谢北京大学工学院湍流与复杂系统国家重点实验室提供的实验设备。

参考文献:

[1]Graf W.Hydraulics of sediment transport[M].New York: McGraw-Hill,1971.

[2]周光炯,严宗毅,等.流体力学[M].北京: 高等教育出版社,1993.

[3]Joseph D D,Liu Y J.Orientation of long bodies falling in a viscoelastic liquid[J].J Rheol,1993,37: 1-22.

[4]Liu Y J,Nelson J,Feng J,et al.Anomalous rolling of spheres down an inclined plane[J].Non-Newtonian Fluid Mechanics,1993,50(2/3): 305-330.

[5]Mollinger A M,Cornelissen E C,van den Brule B H A A.An unexpected phenomenon observed in particle settling: oscillating falling spheres[J].J Non-Newtonian Fluid Mech,1999,86: 389-393.

[6]Merzkirch,Wolfgang.Flow visualization[M].London: Academic Press,1987.

[7]Pankhurst R C,Holder D W.Wind-tunnel technique[M].London: Sir Isaac Pitman & Sons,1952.

[8]Hinze J O.Turbulence[M].New York: McGraw-Hill,1975.

[9]Launder B E,Spalding D B.Lectures in mathematical models of turbulence[M].London: Academic Press,1972.

[10]Snyder D O,Koutsavdis E K,Anttonen J S R.Transonic store separation using unstructured cfd with dynamic meshing[R].AIAA-2003-3913,2003.

作者简介: