基于EEMD气液两相流差压信号时频分析
2014-03-30孙斌,刘彤,赵鹏
孙 斌,刘 彤,赵 鹏
(中国计量学院,杭州 310018)
0 引 言
动态差压波动信号是能反映气液两相流流动状态的特征信号。两相流流体通过节流装置时,由于气、液相介质在节流件局部点上交替流过,故在节流装置的前后产生压力差。差压信号波动性很强,同时具有一定规律性,且信号获取容易,不会影响两相流的流型和流动。V锥流量计作为一种节流装置,由于其测量精度高,性能稳定,压力损失小等优点,被广泛地应用于两相流的研究当中。
1998年,Huang N E等人提出经验模式分解(EMD)算法[1]。EMD算法能将复杂信号分解为若干个固有模态函数(IMF)的集合,并对每个IMF函数进行Hilbert变换得到瞬时频率[2]。EMD具有自适应性和分辨率高的特点,但同时,EMD也存在着模式混叠现象。之后,针对模式混叠现象,Flandrin的法国EMD算法研究小组和Huang的研究小组提出,通过将白噪声加入信号来补充一些缺失的尺度即EEMD(Ensemble Empirical Mode Decomposition)方法,该方法有效地抑制了EMD产生的模态混叠现象,是对EMD方法的重大改进[3]。
EEMD方法已在生物医学工程、气象、声音增强和故障诊断等领域取得良好的效果[4],但在两相流测量中的应用却较为少见。本文创新点在于将此方法应用到两相流流型识别问题上,并通过LabVIEW软件编程,设计前面板和程序框图,对采集的两相流差压信号进行分析,将原始信号分解为多个固有模态函数并进行时频分析。
本研究基于LabVIEW软件编程,采集两相流差压信号,使用总体平均经验模式分解(EEMD)的原理与算法对不同流型信号进行分析,从理论上说明使用EEMD算法能够很好地应用于两相流流型分析。研究的重点在于:使用EEMD算法提取原始信号的各频率分量,避免其他算法出现的模态混叠现象,更准确地分析信号的时变情况。通过两相流流经V锥流量计实验,对两相流的差压信号进行采集,获取动态差压信号。以气液两相流中的泡状流、弹状流和塞状流3种特征流型为主要研究对象。使用PCI6024板卡采集信号,并用EEMD和EMD两种不同方法应用于每种流型的差压信号,对比实验结果,验证EEMD方法在对两相流差压信号的分析上,比EMD有更好的效果,可以为之后两相流流型识别打下基础。
1 EMD基本理论
传统EMD分解的基本思想是将任意非线性、非平稳的随机信号分解为若干个基本模式分量——本征模函数(IMF)和一个趋势项。本征模函数(IMF)是一类关于时间轴局部对称且其过零点与极值点个数相同的函数,分解之后的IMF都是平稳的[5],再将分解的每一个IMF经过Hilbert变换。本征模函数(IMF)要满足2个条件[6]:一是在整个时间序列中,极值点数与过零点数必须相等或最多相差1个;二是在任意时间点上,信号局部极大值确定的上包络线和局部极小值确定的下包络线的均值为零。EMD分解步骤如下[7]:
(1) 确定原始输入信号x(t)的极大值点和极小值点,求取上下包络线的局部均值序列m(t)。
(2) 做运算h1(t)=x(t)-m(t),检测h1(t)是否满足IMF的2个条件。如果不满足,则把h1(t)作为待处理信号,重复上述操作,直到h1(t)满足IMF条件。此筛选过程的停止是通过限制两个连续的处理结果之间的标准差Sd的大小来实现,即
(1)
式中:T表示信号的时间跨度,hk-1(t)和hk(t)是在筛选IMF过程中两个连续的处理结果时间序列。Sd的值通常取0.2~0.3。
(3) 计算信号剩余序列r1(t),即r1(t)=x(t)-c1(t)。
(4) 把r1(t)作为新的“原始信号”重复上述操作,依次可得第2个、第3个至第n个IMF,记为c1(t),c2(t),…,cn(t)。当cn(t)或剩余信号rn(t)小于一个预设值,或者rn(t)是一个单调函数,不能再筛选IMF时,整个分解过程终止。
最终,信号将被分解成:
(2)
这时,分解产生的IMF都是平稳的,从而能更好的帮助分析原始非线性非平稳的随机信号。
2 EEMD基本理论
在对信号进行EMD分解过程中,需要取信号上下包络的平均,所以当信号的时间尺度存在跳跃性的突变时,则不可避免地会出现IMF分量包含不同的尺度特征或者一个时间尺度分布在不同的IMF中,也就是模态混叠现象[8]。为了更好地解决这种现象,Huang提出了EEMD算法,一种噪声辅助信号处理方法[9]。
一般情况下,人们都是从信号中消除噪声,提取真实信号。而EEMD则是利用白噪声的频谱均匀分布的特性,将白噪声加入整个待分析的信号中。当信号加在白噪声的背景上时,不同时间尺度的信号会自动映射到合适的参考尺度上[10]。而且由于零均值噪声的特性,经过多次平均,噪声相互抵消,从而得出最接近原始信号的结果。EEMD分解的过程如下[11]:
(1) 在目标数据上加上白噪声序列;
(2) 将加入高斯白噪声的序列按照EMD算法分解为IMF;
(3) 每次加入相同幅值的不同高斯白噪声序列,重复上述2个步骤;
(4) 把分解得到的各个IMF的均值作为最终的结果,即:
(3)
式中:cj(t)是对原始信号进行EEMD分解得到的第j个IMF分量;N是加入白噪声的次数。
3 气液两相流差压信号的分析
气液两相流的差压信号,能够较好地反应两相流的流动特征。当两相流流型变化时,差压信号和频率分布带的改变相对明显。目前主要的差压式节流装置有孔板、文丘里管、V型内锥和多孔孔板[12],本实验主要选用V型内锥流量计。
3.1实验测试方案及装置
实验以水平管道气液两相流动在节流装置前后所产生的差压信号为研究内容。实验管段为口径50mm的钢管,实验介质为空气和自来水。实验装置如图1所示。

图1 两相流管道装置示意图
由气泵产生的压缩空气由储气罐通过50mm口径的钢管。钢管装有流量调节阀和标准表等装置,调节阀用来进行气流量大小的调节,从而控制流型[13];旋进旋涡流量计计量气流量大小。水同样在另一50mm管道经过调节阀和电磁流量计之后,与气体管道中的空气在气水混合器重新进行混合,再经过一个总调节阀进入50mm口径实验管道中。有机玻璃观察管段可以用来目测流型。V型内锥流量计安装在实验段,用来检测流体流过的前后压差。最后,经过实验管段的两相流进入标准容器,气体进入大气,水继续循环使用。
实验中安装的节流装置为V型内锥流量计,简称V锥,用以产生差压波动信号。V形内锥流量计如图2所示,在封闭的管流系统中同轴安装一节流体,其由圆锥与圆台构成[14],流体流动方向如图2所示。

图2 V型内锥流量计结构图
为了避免动态信号在采集过程中出现失真,选用硅式差压变送器HM31,其采用德国HELM公司的差压敏感芯片,主要参数为:量程范围0~50kPa,精度为0.8%,响应时间为1ms,频率响应为1kHz[16]。
实验中数据采集卡选择美国国家仪器公司生产的NI-PCI6024E采集板卡。NI-PCI6024E采集卡可在大多数应用中实现可靠的高性能数据传输,具有高达200 kS/s的采样率,12位分辨率[15]。由于数据采集卡采集范围为-10~10V,而差压变送器输出的是4~20mA的电流信号,因此,电流信号需要在电路中通过250的电阻将其转化为1~5V电压信号再通过数据采集卡进行采集。
3.2信号处理分析
基于LabVIEW的信号采集及处理系统采用200Hz的频率对差压信号进行采样。此采样频率符合恩奎斯特采样定理,fs≥2fH,能较完整地重现原始信号。
在提取两相流差压信号的实验中,保持水流量不变,通过改变气体流量,实现泡状流、弹状流和塞状流3种不同流型。各工况流型的气液量大小如表1所示。

表1 不同流型气液量
首先以塞状流差压信号的分析为例,分别比较EMD与EEMD 2种处理方法结果的不同,从而对EEMD分解方法及效果进行解释说明。塞状流原始差压信号波形图如图3所示。
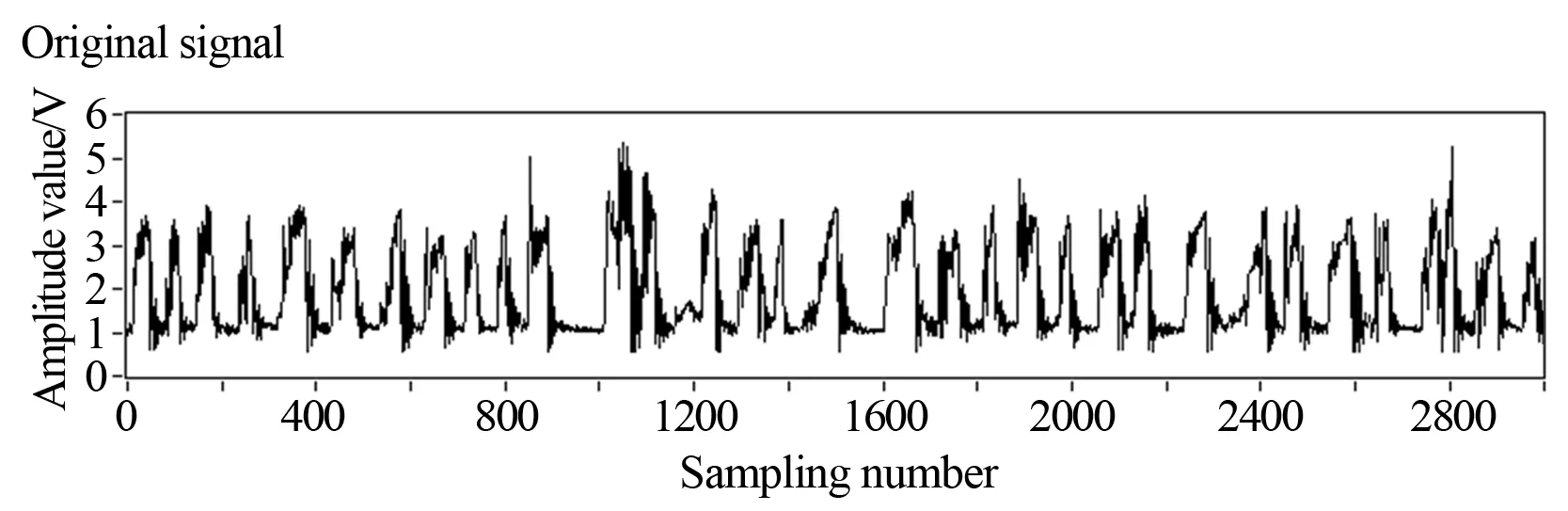
图3 塞状流差压信号波形图
图3是采用200Hz频率对塞状流的差压信号进行采集的原始信号波形图。实验中横坐标表示采集了3000点,通过换算也就是15s,纵坐标为差压信号的幅值,以电压表示。
首先,分别采用EEMD与EMD 2种方法,对上图中塞状流的差压信号进行分析比较。塞状流的特点是气弹存在于管道,且直径基本接近管道内径,气液两相界面非常明显。当流体通过V型内锥流量计时,波动将更加明显。
将图3中的差压信号用EMD方法进行分解,产生的IMF如图4所示。EMD自适应地将原始信号分解成8个IMF分量,最后R为残余项。
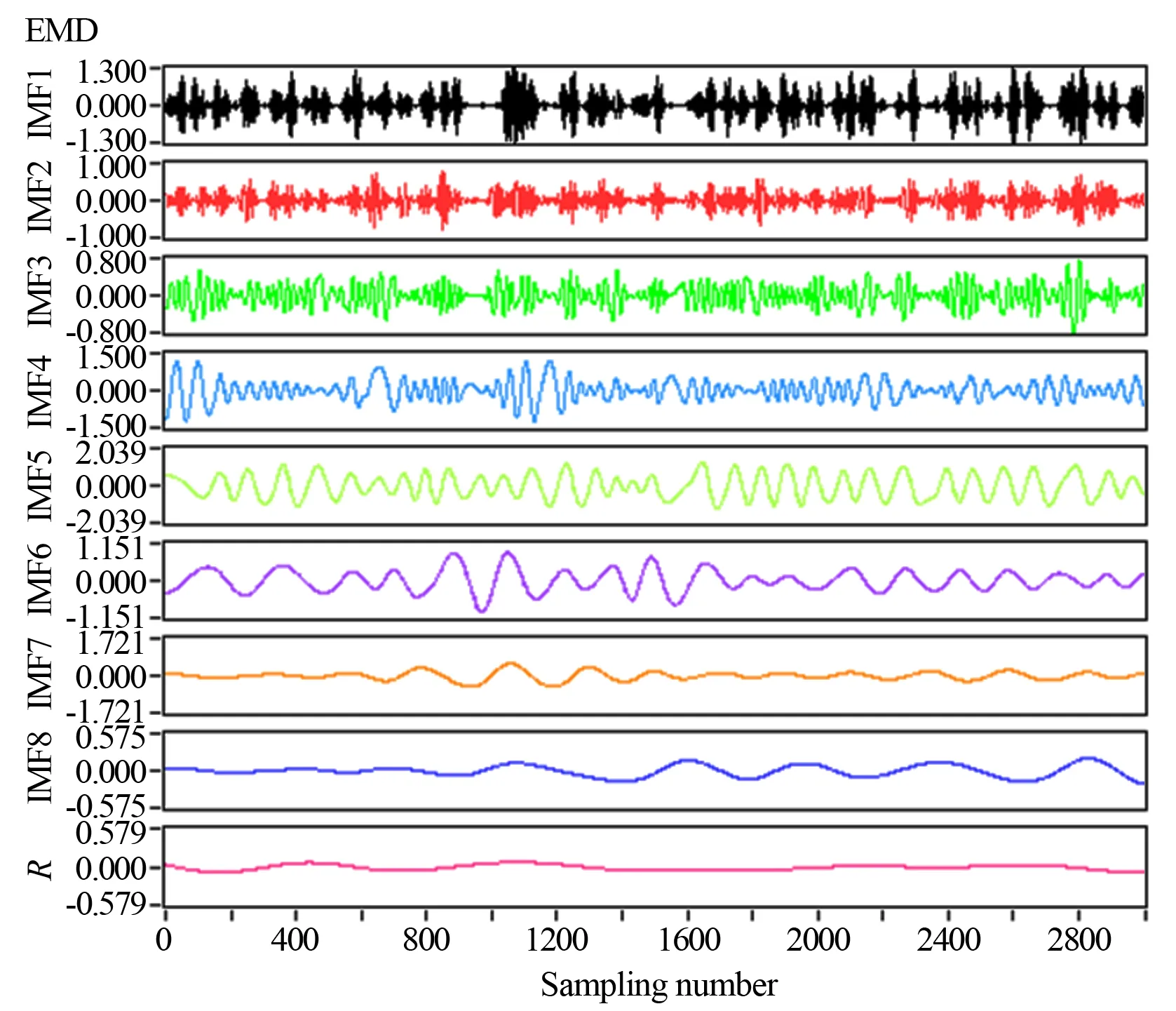
图4 EMD分解塞状流差压信号所得IMF
从图4中可以看出,非平稳的两相流差压信号被分解成了若干个平稳的IMF分量之和,不同的IMF分量包含了不同的时间尺度。
在EMD分解实际信号的过程中,为了更清楚了解每个IMF所包含的频率及能量信息,对每个IMF分量进行频谱分析,如图5所示。可以发现,1~4Hz的低频分量混叠在一起,难以分辨。
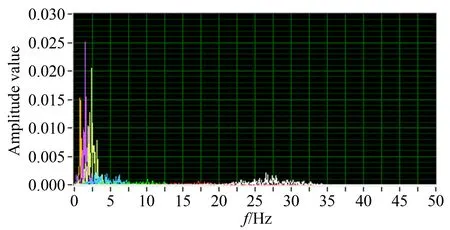
图5 EMD分解塞状流差压信号Hilbert频谱图
在原始信号中,加入白噪声进行EEMD分析。一般情况下,根据Huang[3]在论文中提出的建议,进行EEMD处理的白噪声方差选择在0.1~0.4之间。本实验选择方差为0.2的白噪声,组数选择100组,进行分解的结果如图6所示。EEMD算法自适应地将原始信号分解为10个IMF分量,最后一个为残余分量R。
同理对EEMD分解的IMF分量进行频谱分析,如图7所示。将其与图5进行对比,可以发现在1~3Hz之间,明显看到信号含有2个频率分量,而信号能量主要集中在2.5Hz左右。相比较于EMD算法,信号的分解结果有较大的改进。
将EMD和EEMD两种方法分解的IMF信号分别做Hilbert变换,得到IMF信号的时频谱如图8和9所示。

图6 EEMD分解塞状流差压信号所得IMF

图7 EEMD分解塞状流差压信号Hilbert频谱图
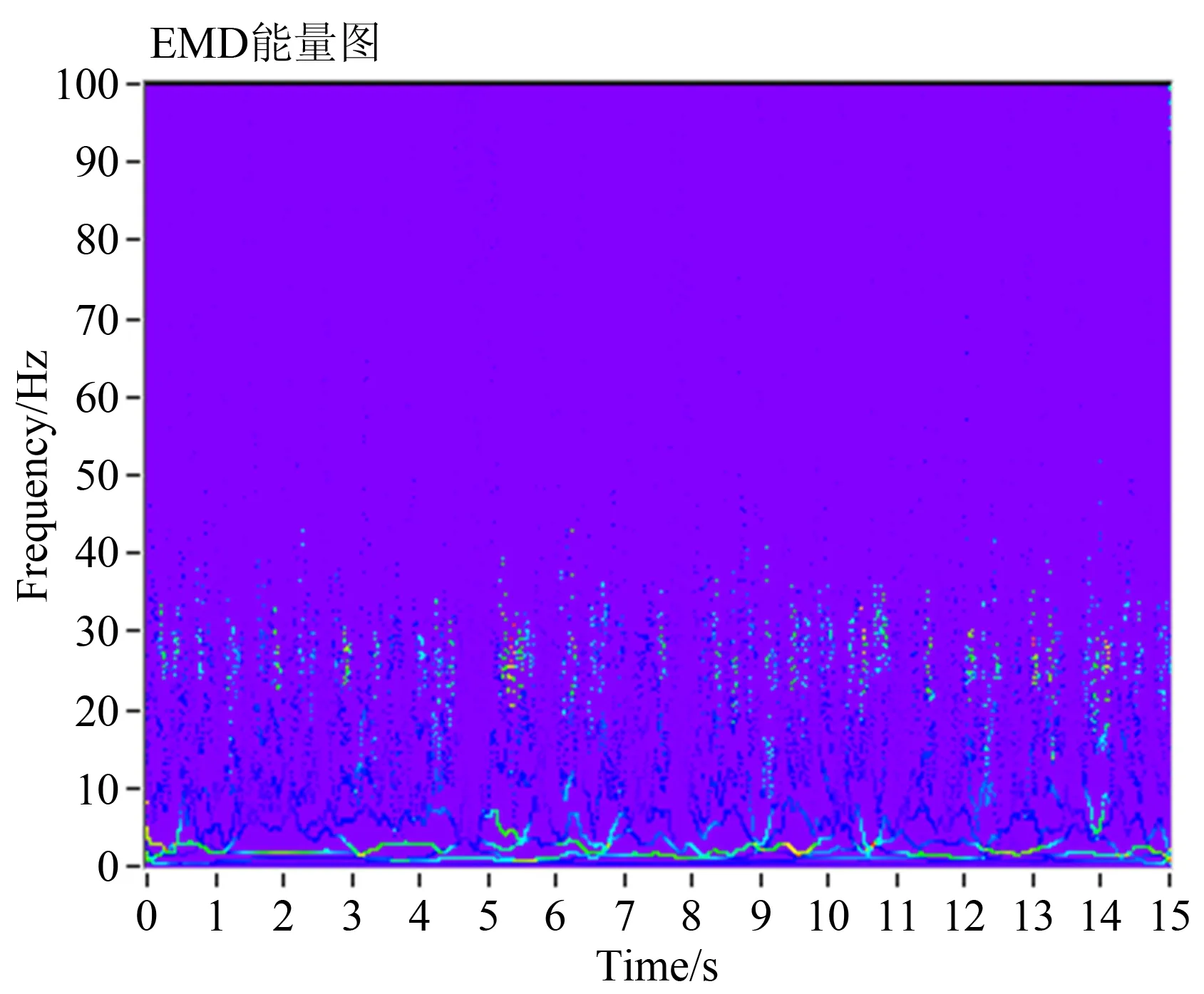
图8 塞状流EMD分解时频图
由Hilbert时频谱可以直观地看出,相比较于EMD分解,EEMD更能突出塞状流差压信号的主要频率成分在3Hz左右。其次以30Hz为中心,在20~40Hz的频带上有少量能量分布。而EMD的分析,除以上分析的频带范围内存在能量分布,在5~20Hz的频带上还显示有交叉干扰能量,说明EMD方法没有EEMD的分解效果好。相比而言,根据频谱图,可以发现EEMD的Hilbert时频图能够更准确地说明差压信号的频率分布。

图9 塞状流EEMD分解时频图
因此,可以说EEMD的分解方法优于EMD的分解方法,能更清楚地显示各频率信号的分布情况,有效消减低频信号的频率混叠现象,并且对差压信号有很好的分解作用。
按同样的方法再分别对两相流中最明显流态——泡状流和弹状流进行分析,可以得到如图10和11所示的结果。分析以上流型的时频图可以看出,3种流型的频率分布不同。泡状流主要分布在20~30Hz频带的范围内,EEMD方法有效地将0~10Hz的干扰频率消除了。弹状流差压信号主要分布在20~30Hz以及1~5Hz 2个频率范围内,在这2个频带内,信号有较大的能量。

图10 泡状流EEMD分解时频图
不同流型的差压信号的频率分布是不同的,信号的能量分布也会随之发生改变。为了讨论EMD和EEMD分解的IMF的能量分布,从而研究不同流型的特征,引入能量熵的概念。由对差压信号x(t)的分解得到的n个IMF,可以相应的计算出其各自的能量E1、E2…En,从而形成了不同流型差压信号在频率域的能量分布。能量熵定义为:

图11 弹状流EEMD分解时频图
(4)

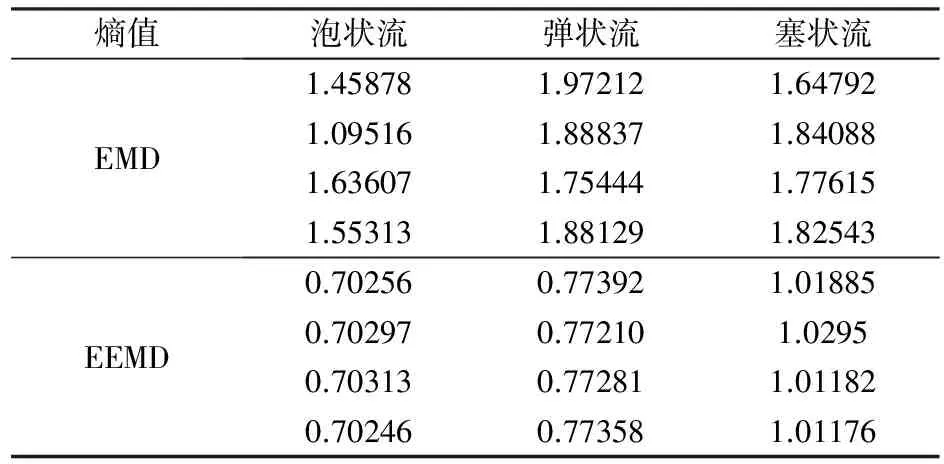
表2 不同流型能量熵对比
横向对比表2中的能量熵可以看出,EMD分解所得各个流型的IMF分布没有明显区别,模态混叠严重,纵向对比能量熵值,则可以发现EEMD分解相较EMD对不同流型有较好的区分度。
从泡状流到塞状流,由表1可知,气量是逐渐加大的。由于气量的增加,管道中的气泡也变得越来越大,流过V锥流量计的流体前后差压变化也越大,具有更高的能量。因此,由EEMD分解所得能量熵是由泡状流到塞状流越来越大。
实验表明,使用EEMD分解方法进行差压信号的分析处理,得出的时频谱图中,3种主要流型特征明显,实验结果准确,且具有较好的分辨率。通过能量熵的计算,可以发现EEMD算法能有效地消除EMD的模态混叠现象,有较好的分辨力。能量熵大小与两相流流型有紧密的关系,可为今后流型的识别研究打下良好的基础,具有较高的研究价值。
4 结 论
阐述了EEMD方法的基本原理与实现步骤,并将其与EMD方法进行比较,证明EEMD可以很好地避免模态混叠。同时,将EEMD方法应用于对气液两相流差压信号的分析研究,得出不同流型的IMF分量以及Hilbert时频谱,发现不同流型的频率分布范围明显不同。能量熵概念的引入为EEMD算法优于EMD算法提供了有力的支持。综合分析之后可以得出结论:EEMD能够较好地处理非线性非平稳的差压随机信号,并将不同流型的特征频率提取出来,为气液两相流流型及流量的准确测量奠定理论基础。
参考文献:
[1]Huang N E,Shen Z,Long S R,et al.The empirical mode de-composition and Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceedings of the Royal of London Series A,1998,454: 903-995.
[2]时世晨.基于 EEMD 的信号处理方法分析和实现[J].现代电子技术,2011,34(1): 88-90.
Shi Shichen,Shan Peiwei.Signal processing method based on ensemble empirical mode decomposition[J].Modern Electronics Technique,2011,34(1): 88-90.
[3]Wang Erpeng,Sun Bin,Qian Fei.Design of fuzzy identification system for patterns of gas-liquid two-phase flow on LabVIEW[C]//Peihua Qiu.2009 2ndInternational Congress on Image and Signal Processing.Tian Jin,2009: 4411-4414.
[4]孙斌,张宏建.基于HHT的两相流动态信号提取与滤波的研究[J].传感技术学报: 2007,20(4): 862-865.
Sun Bin,Zhang Hongjian.Research on extract and filter of dynamic signal of two-phase flow based on HHT[J].Chinese Journal of Sensors and Actuators,2007,20(4): 862-865.
[5]胡爱军.Hilbert-Huang 变换在旋转机械振动信号分析中的应用研究[D].保定: 华北电力大学,2008.
Hu Aijun.Research on the application of Hilbert-Huang transform in vibration signal analysis of Rotating machinery[D].North China Electric Power University(Hebei),2008.
[6]刘涛.基于EEMD和HT的轴流泵压力脉动特征信息提取[J].机电工程,2012,29(3): 278-281.
Liu Tao,Huang Qibai.Characteristic information extraction of pressure pulsation signal in axis-flow pump based on EEMD and HT[J].Journal of Mechanical & Electrical Engineering,2012,29(3): 278-281.
[7]王强,周云龙,崔玉峰,等.EMD与神经网络在气液两相流流型识别中的应用[J].工程热物理学报,2007,28(3): 442-444.
Wang Qiang,Zhou Yunlong,Cui Yufeng,et al.Applied study of EMD and neural networks on flow regime identification for gas-liquid two-phase flow[J].Journal of Engineering Thermophysics,2007,28(3): 442-444.
[8]Hubbard M G,Dukler.The characterization of flow regimes for horizontal two-phase flow[C]//Proceedings of 1996 Heat Transfer and Fluid Mechanics Institute.Stanford University Press,1996: 100-121.
[9]王强.基于小波和希尔伯特-黄变换的气液两相流流型智能识别方法[D].吉林: 东北电力大学,2007.
Wang Qiang.The identification method of gas-liquid two-phase flow regime based on wavelet and Hilbert-Huang transform[D].Northeast Dianli University,2007.
[10]Rubini R,Meneghetti U.Application of the envelope and wavelettransform analyses for the diagnosis of incipient faults in ball bear-ings[J].Mechanical Systems and Signal Processing,2001,15(2) : 287.
[11]王谨敦.基于EEMD的故障微弱信号特征提取研究[J].电子设计工程,2011,20(14): 72-74.
Wang Jindun,Chen Lue,Qu Wei.Research on fault weak signal feature extraction based on EEMD method[J].Electronic Design Engineering,2011,20(14): 72-74.
[12]梁法春,曹学文,林宗虎等.多相流流型检测与识别技术[J].油气储运,2001,20(11): 1-4.
Liang Fachun,Cao Xuewen,Lin Zonghu,et al.Multiphase flow regime measurement and identification techniques[J].Oil & Gas Storage and Transportation,2001,20(11): 1-4.
[13]孙斌.基于HHT与SVM的气液两相流双参数测量[D].浙江: 浙江大学,2005.
Sun Bin.Gas-liquid two-phase flow bi-Parameters measurement based on the HHT and SVM[D].Zhejiang University,2005.
[14]Meng Zhenzhen,Huang Zhiyao,Wang Baoliang,et al.Air-water two-phase flow measurement using a Venturi meter and an electrical resistance tomography sensor [J].Flow Measurement and Instrumentation,2010,21(3): 268-276.
[15]孙斌,张宏建,岳伟挺.HHT与神经网络在油气两相流流型识别中的应用[J].化工学报,2004,55(10): 1723-1727.
Sun Bin,Zhang Hongjian,Yue Weiting.Applied study of HHT and neural networks on flow regime identification for oil-gas two-phase flow[J].Journal of Chemical Industry and Engineering(China),2004,55(10): 1723-1727.
[16]Wu Zhaohua.Ensemble empirical mode decomposition: a noise-assisted data analysis method[J].World Scientific,2009,1(1): 1-41.
[17]周云龙,洪文鹏,孙斌.多相流体力学理论及应用[M].北京: 科学出版社,2008.
作者简介:

孙斌(1972-),男,黑龙江勃利人,博士,教授。研究方向:多相流参数检测及信号处理应用。通信地址:浙江省杭州市下沙高教园区学源街中国计量学院计量测试工程学院(310018)。E-mail:bsun555@cjlu.edu.cn
