泡沫金属圆管内沸腾传热的数值模拟

孙 斌，崔彬彬，梁 超

(东北电力大学 能源与动力工程学院，吉林 吉林 132012)

多孔泡沫金属是一种以金属为基体并含有一定数量、一定尺寸孔径、一定孔隙率的金属材料［1］。对于开孔泡沫金属，其互通的网状结构有着极大的面容比，使得固体与流经的液体有着极好的接触换热，因此传热效率大大提高，成为众多学者的研究对象［2－11］。

Simone Mancin［2］对空气通过具有不同PPI和渗透率的泡沫金属进行了实验研究，并给出了压降关联式。赵长颖［3］等对填充泡沫金属圆管中流动沸腾传热现象进行了实验研究，研究表明泡沫金属圆管中传热系数是光滑管中的三倍。徐治国［4］等对烧结有厚度为30 mm高孔隙率通孔铜泡沫的水平表面的池沸腾进行实验研究，并采用高速摄像仪对泡沫表面的汽泡生长形貌进行了可视化研究。Brahim Madani［5］以正戊烷为工质，实验研究了管壁处烧结泡沫金属的沸腾传热现象。胡海涛［6－7］等实验研究了泡沫金属对制冷剂－油混合物在水平管内流动沸腾传热系数和压降的影响，并开发制冷剂－油混合物通过泡沫金属的压降预测关联式。朱禹［8］等采用Mixture多相流模型对泡沫金属内液体流动沸腾进行的模拟研究。孙硕［9］等分别对填充5PPI和10PPI泡沫金属的圆管中R410A流动沸腾两相流压降特性进行了实验研究，开发了适用于填充泡沫金属内径13.8 mm圆管中的流动沸腾的压降关联式。李盈海［10］等对空气在金属泡沫管内的强制对流换热进行了二维数值模拟，发现金属泡沫管的努塞尔数随孔隙率的减小或孔密度的增加而增大，且随流体和固体导热系数比值的减小而增大;金属泡沫管的强化换热效果十分明显，但其压降远大于光管。李景灏［11］等对壳程流体纵掠多孔泡沫金属中的传热管外表面的流动和传热进行了试验研究，并用Brinkman－Forchheimer Darcy流动模型和局部非热平衡传热理论对纵掠传热管外的对流传热进行了理论分析。

目前对于泡沫金属中单相介质流动问题，实验和数值研究方面已有不少研究成果，但对于泡沫金属中多相介质流动问题的研究还相对较少。因此，本文在建立泡沫金属圆管内沸腾传热模型的基础上，采用Fluent软件进行数值模拟，研究了管内的压降、流型及传热系数与质量流率、干度的变化关系，以期了解泡沫金属管中沸腾强化换热的机制，促进工业化应用和推广。

1 数值模拟过程

1.1 数学模型

为了计算方便，更好地建立数学模型，对模型做如下简化:(1)泡沫金属是均匀的且各向同性;(2)工质为不可压缩流体;(3)工质的物理性质不随温度发生变化;(4)忽略自然对流与辐射传热。

泡沫金属内两相的流动模型:

连续方程

式中 ρm——混合密度(α相的体积分数)，ρm=∑αkρk;

m

动量方程

式中 μm——混合粘度，μm=∑αkμk;

g——重力加速度;

SM——动量源项。

能量方程

式中 Hm——混合比焓，Hm=∑αkHk;

ε——泡沫金属孔隙率;

ρs——固体密度;

keff——有效热导率，计算式如式(4)。

式中 kl、kv、ks——液相、气相和固相的导热系数。

1.2 动量源项

由于泡沫金属对流体动量传递的影响，SM动量源项可由Brinkman－Forchheimer［12］获得

式(5)中右侧第一项为传统意义的Dancy项，表示粘性损失，右侧第二项为非线性修正项，表示内部损失。

根据Bhattacharya等［13］的研究，泡沫金属的渗透率K及惯性系数C可由下式获得

1.3 沸腾模型

沸腾相变主要伴随着相间的质量传递和能量传递过程，Fluent软件中没有沸腾模型，需要通过自定义函数UDF来实现。

根据De Schepper等［14］研究，对于质量传递过程，质量源项的计算表达式如下

式中 Tl、Tv、Tsat——液相温度、气相温度和饱和温度。

能量源项计算表达式如下

式中 ΔH——潜热。

1.4 计算区域及边界条件

本文采用与赵长颖［3］等人的实验相同条件进行模拟，模型为150 mm×φ26 mm泡沫铜(PPI= 20，ε=0.9)圆管，工质为R123a。采用Gambit软件进行网格划分，通过网格无关性讨论，确定最佳网格数量为164 128。设置入口边界条件为速度入口，入口温度为操作压力下的饱和温度，出口为自由出口，壁面采用定热流密度边界条件q=19 kW/m2，无滑移。

图1 物理模型及网格划分

2 模拟及结果分析

采用Fluent6.3.26软件根据所建立的物理模型和数学模型，对泡沫金属圆管沸腾传热现象进行数值模拟。模拟采用三维非定常压力基求解器，VOF多相流模型，压力－速度耦合方法为SIMPLY算法，每次模拟过程中，时间步长和松弛因子需要适当地进行调整以保证收敛。

2.1 压降

图2给出了给定质量流率下，泡沫金属圆管单位长度压降随干度的变化情况，模拟的结果与已有实验数据［3］符合较好。由图中可以看出在一定质量流率下，泡沫金属管单位长度压降随着干度的增大而增大，且成非线性增长趋势，这是因为干度增大，气相的体积分数增大，气相的速度增大，从而导致压降的增大。同时，当干度一定时，泡沫金属圆管单位长度压降随着质量流率的增大而增大，根据Steiner［15］研究表明，当管内气液两相流干度一定时，质量流率大则气相体积分数大，导致气相速度大，从而导致压降大。而另一方面，质量流率大也直接导致工质流速较大，从而导致压降较大。

2.2 流型分析

图2 不同质量流率下，单位长度压降随干度的变化

图3 x=0.6，G=106 kg/m2·s管内气相体积分数随时间的变化

图3是干度为0.6，质量流率为106 kg/m2·s的制冷剂在泡沫金属圆管中气相体积分数随时间的变化情况。由图3可以看出，在模拟的开始阶段，气相在泡沫金属圆管中均匀分布(如图3(a))，当t=3 s时，泡沫金属管中出现了部分液相聚集区(如图3 (b))，这是由于泡沫金属的孔径较小，气液两相在流过泡沫金属的过程中，粘性较大的液相在泡沫金属的基体上聚集，随着时间的增长，液相聚集增多，脱离泡沫金属基体，同时，由于质量流率较大，导致流速较大，液相最终聚集在靠近管壁处，形成环状流(如图3(c))。

图4是制冷剂质量流率为106 kg/m2·s，流型稳定后，管内同一截面处气相体积分数随干度的变化情况。由图4可以看出G=106 kg/m2·s，当干度较低时，气相集中于部分区域，由于质量流率较大，形成弹状流流动(如图4(a))。随着干度的增大，气相体积分数逐渐增大，几乎占聚整个圆管内部，只有少量液相占聚圆管靠近壁面部分，形成环状流流动(如图4(b))。

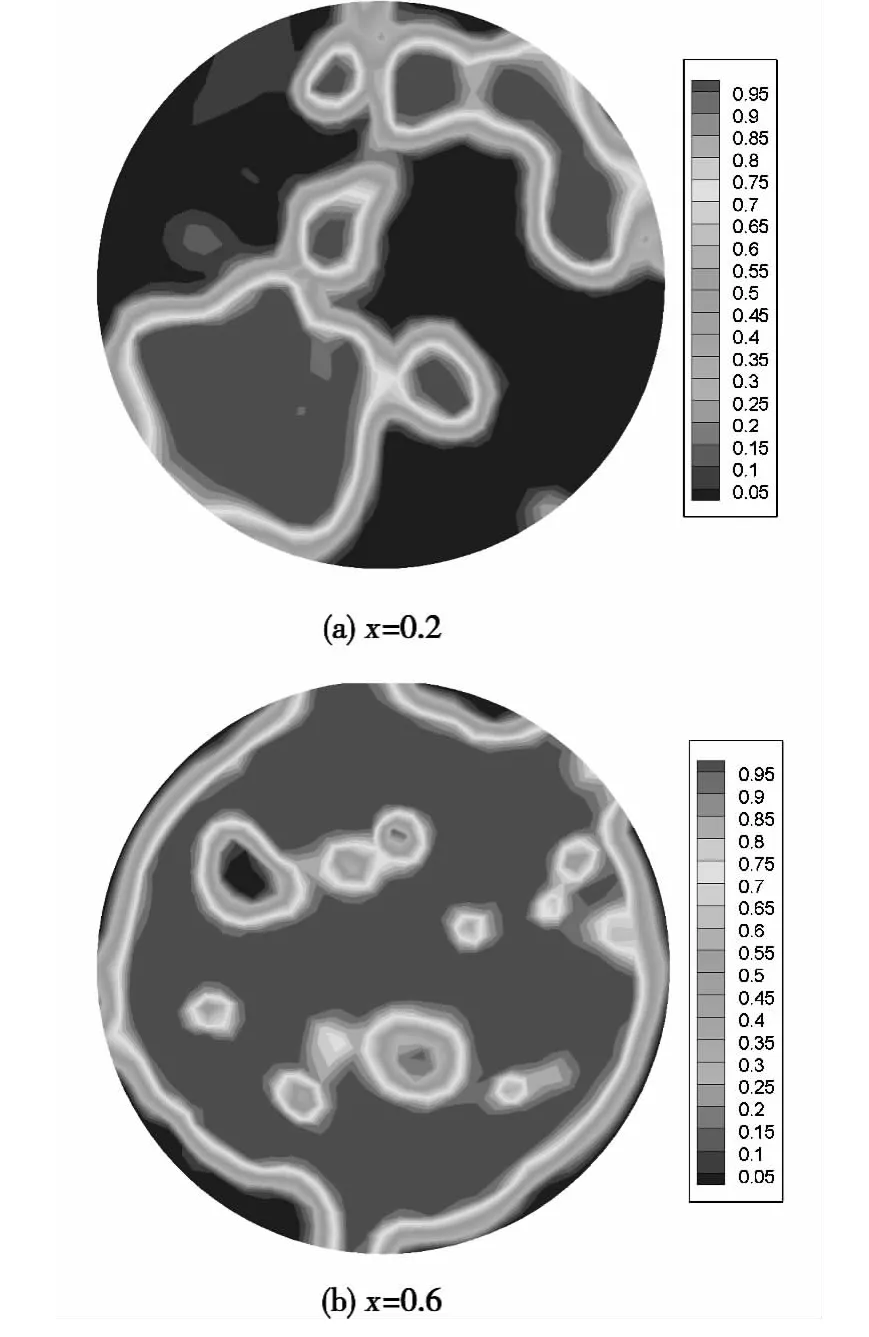
图4 G=106 kg/m2·s时泡沫金属管同一截面处气相体积分数随干度的变化

图5是制冷剂质量流率为26 kg/m2·s，流型稳定后，泡沫金属圆管同一截面处气相体积分数随着干度的变化情况。由图中可以看出G=26 kg/m2· s，当干度较低时，由于受重力的作用，气相占聚泡沫金属管的上部份，液相占聚圆管的下部分，形成分层流(如图5(a))。随着干度的增大，流速增大，流型由相界面分明的分层流变成相界面剧烈变动的波动流(如图5(b)(c))，干度进一步增大，气相增多，管内形成了液相只占聚圆管低层的稳定的波状流(如图5(d))。

图5 G=26 kg/m2·s稳定后，泡沫金属管中气相体积分数随干度的变化

图6为根据本文模拟的大量数据所得出的泡沫金属管内两相流流型与质量流率、干度的关系图。由图中可以看出，当质量流率较小时，干度小于0.35时，泡沫金属管中流型为波状流，而干度大于0.35时，流型为稳定的波状流。

图6 泡沫金属管内流型与质量流率、干度关系图

2.3 传热系数分析

图7给出了传热系数随质量流率、干度的变化。由图中可以看出，当质量流率较低时，传热系数随着干度的增大而减小，这是因为干度逐渐增大，在流型由波状流过渡到稳定波状流过程中，液相与壁面的接触面面积逐渐变小，导致传热系数下降。当质量流率较高时，传热系数随着干度的增大而增大，这是因为干度逐渐增大，流型由弹状流过渡到环状流，液相与壁面的接触面面积逐渐增大，导致传热系数的增大，且大质量流率时，传热系数变化幅度较小。

图7 传热系数随质量流率、干度的变化

3 结论

(1)建立了泡沫金属圆管中沸腾传热模型，并用fluent软件进行模拟，模拟结果与文献中的实验数据符合较好。

(2)在一定质量流率时，泡沫金属圆管单位长度压降随着干度的增大呈非线性增长关系;在一定干度时，泡沫金属圆管单位长度压降随着质量流率的增大而增大。

(3)低质量流率时，泡沫金属圆管中流型由分层流过渡到波状流;高质量流率时，泡沫金属圆管中流型由弹状流过渡到环状流。给出了泡沫金属圆管中流型与质量流率、干度的关系图。

(4)低质量流率时，传热系数随着干度的增大而减小。高质量流率时，传热系数随着干度的增大而增大。

［1］汪双凤，李炅，张伟保.开孔泡沫金属用于紧凑型热交换器的研究进展［J］.化工进展，2008，27(5):675－678.

［2］Simone Mancin，Claudio Zilio，Alberto Cavallin.Preeure drop during air flow in aluminum foams［J］.International Journal of Heat and Mass Transfer，2010，53:3121－3130.

［3］Zhao C.Y，Lu W，Tassou S.A.Flow Boiling Heat Transfer in Horizontal Metal－Foam Tubes［J］.Journal of Heat Transfer，2009，131(12):121002－8.

［4］徐治国，屈治国，李定国，等.通孔金属泡沫表面的池沸腾实验研究［J］.工程热物理学报，2009，30(10):1713－1716.

［5］Brahim Madani，Lounes Tadrist，Frederic Topin.Experimental analysis of upward flow boiling heat transfer in a channel provided with copper metallic foam［J］.Thermal Engineering，2013，52:336－344.

［6］Zhu Yu，Hu Hai tao，Ding Guoliang，et al.Influence of metal foam on heat transfer characteristics of refrigerant－oil mixture flow boiling inside circular tubes［J］.Thermal Engineering，2013，50:1246－1256.

［7］Hu Haitao，Zhu Yu，Ding Guoliang，et al.Effect of oil on two－phase pressure drop of refrigerant flow boiling inside circular tubes filled with metal foam［J］.International Journal of Refrigeration，2013，36:516－526.

［8］朱禹，胡海涛，丁国良.泡沫金属内液体流动沸腾热质传递过程的模拟［J］.化工学报，2010，61(2):30－34.

［9］孙硕，胡海涛，丁国良，等.泡沫金属对圆管内R410A流动沸腾压降特性的影响［J］.化工学报，2012，63 (11):3428－3433.

［10］李盈海，陶文铨，孙东亮，等.金属泡沫管内强制对流换热的数值模拟［J］.西安交通大学学报，2008，42(3): 261－264.

［11］李景灏，李菊香，缑清鸽，等.流体纵掠多孔泡沫金属换热器中顺列传热管外表面的试验研究［J］.热能动力工程，2011，26(3):304－309.

［12］刘伟，范爱武，黄晓明.多孔介质传热传质理论与应用［M］.北京:科学出版社，2006.

［13］Bhattacharya A，Calmidi V V，Mahajan R L.Thermophysical properties of high porosity metal foams1International［J］.Journal of Heat and Mass Transfer，2002，45(5):1017－1031.

［14］S.C.K.De Schepper，G.J.Heynderickx，G.B.Marin，Modeling the evaporation of a hydrocarbon feedstock in the convection section of a steam cracker［J］.Computers＆Chemical Engineering，2009，33(10):122－132.

［15］D.Steiner，J.Taborek，Flow boiling heat－transfer in vertical tubes correlated by an asymptotic model［J］.Heat Transfer Engineering，1993，14(3):61－67.