一种新的曲线曲面

严兰兰， 韩旭里

(1.东华理工大学理学院，江西 南昌 330013；2.中南大学数学与统计学院，湖南 长沙 410083)

Bézier方法和B样条方法在计算机辅助几何设计中占有重要地位，它们各有各的优点，但并不意味它们已经完美无缺，因此不断有文献提出新的造型方法来对这两种传统的造型方法进行改进，目前的改进主要集中在两个方面：一是通过构造具备Bernstein基函数或B样条基函数基本性质，但含参数的新的基函数，使得由之定义的曲线曲面在具备Bézier曲线曲面[1-6]或B样条曲线曲面[7-10]的基本性质之外，还具备形状可调性，从而实现提高传统造型方法形状调整灵活性的目标；二是通过在非多项式空间，如三角函数空间、双曲函数空间、指数函数空间上构造具备Bernstein基函数或B样条基函数基本性质的新的基函数，使得由之定义的曲线曲面在具备Bézier曲线曲面[11-15]或B样条曲线曲面[16-22]的基本性质之外，还能表示一些圆锥曲线曲面和超越曲线曲面，从而实现扩大传统造型方法形状表示范围的目标。

注意到Bézier方法虽然简单、直观，但单一的Bézier曲线曲面往往无法表达复杂的形状，因此在工程实际中，常常需要将多条Bézier曲线段、多张Bézier曲面片组合在一起。为了保证组合曲线曲面的光滑性，相邻Bézier曲线段、Bézier曲面片的控制顶点间必须满足一定的连续性条件。通常情况下，对连续性的求越高，条件越复杂，条件中涉及到的控制顶点的数量越多。能否构造新的曲线，使之能在相对简单的条件下达到较高阶的光滑拼接呢？

注意到虽然B样条方法可以自动解决Bézier方法面临的光滑拼接问题，但是B样条曲线曲面中各条曲线段、各张曲面片的阶必须相同，若选择用不同阶的B样条曲线段、曲面片来描述复杂形状，同样需要解决光滑拼接问题。另外，虽然B样条方法具有局部控制性，但因为B样条曲线相邻曲线段只有一个控制顶点不一样，其他控制顶点全部公共，所以B样条方法的局部控制能力随着阶的升高而减弱。能否构造新的分段组合曲线，使之像B样条曲线一样，无需对控制顶点附加任何其他条件，便能自动实现光滑拼接，并且组合曲线的各条曲线段可以取不同的阶，组合曲线具有比B样条曲线更强的局部控制能力呢？

为了实现上面提到的这些目标，这里构造了n(n≥2)阶混合函数并由之定义了n阶新曲线。新曲线具有Bézier曲线除端点插值以外的基本性质。在拼接时，只要前一条曲线的最后一条控制边与后一条曲线的第一条控制边重合，两条新曲线间便可以达到G2光滑拼接。考虑到新曲线这种特殊的几何拼接条件，我们用类似于但又不同于B样条曲线的组合定义方式定义了由新曲线构成的分段组合曲线。这种组合曲线在分段连接点处可以自动实现G2光滑拼接，各分段曲线控制顶点的数量(大于等于3个)可以自由选择，移动一个控制顶点，至多改变两条分段曲线的形状。

1 混合函数及其性质

1.1 混合函数的定义

定义1.对t∈[0,1]，称：

为2阶混合函数。记s=称：

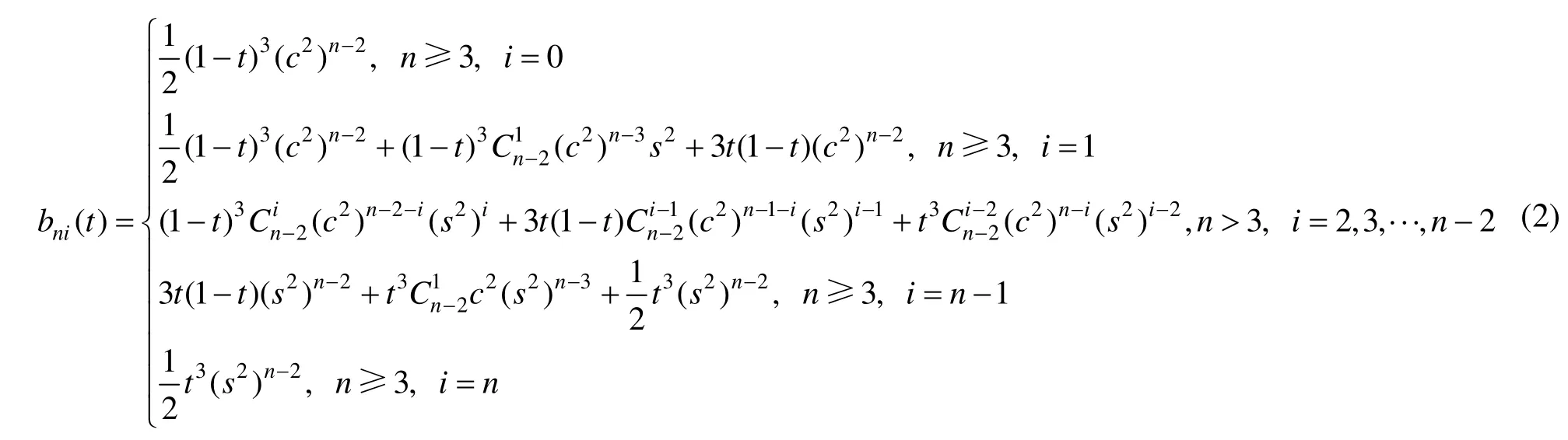
为n阶混合函数。

为了简洁，在不至于引起混淆时，下文中将bni(t)简记为bni，这里n≥2，i=0,1,…,n。

图1～4所示为2～5阶混合函数的图形。

1.2 混合函数的性质

由式(1)～(2)易知混合函数具有下列性质：

(1) 非负性，任意n阶混合函数bni≥0，这里n≥2，i=0,1,…,n。

(2) 规范性，对任意的n≥2，

(3) 对称性，对任意的n≥2，i=0,1,…,n，当t∈[0,1]时，有bni(t)=bn,n-i(1-t)。

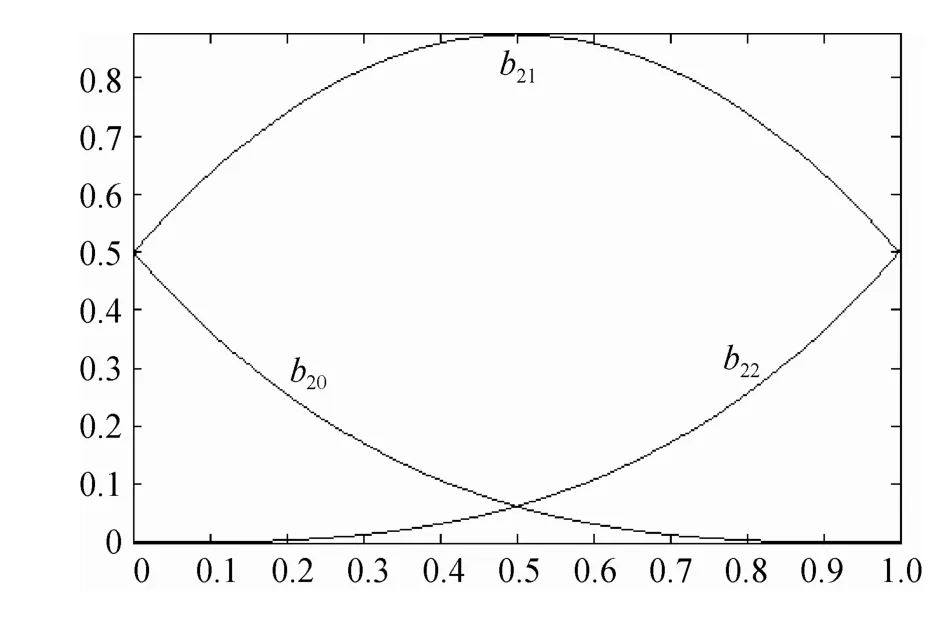
图1 2阶混合函数

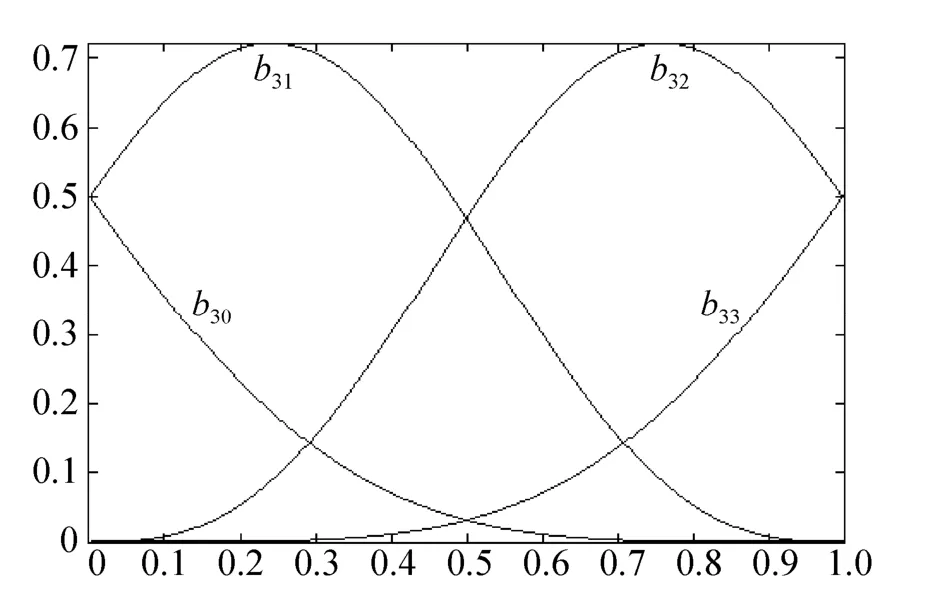
图2 3阶混合函数

图3 4阶混合函数

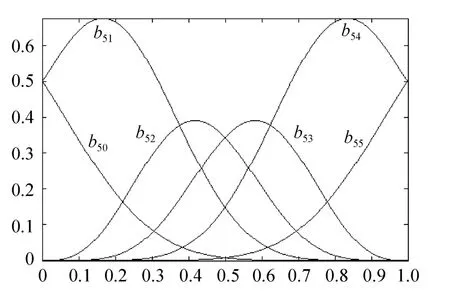
图4 5阶混合函数

(4) 端点性质，对任意的n≥2，i=0,1,…,n，有：

证明.当n=2时，由式(1)经过简单的计算易知式(3)～(4)中结论正确。当n≥3时，记：

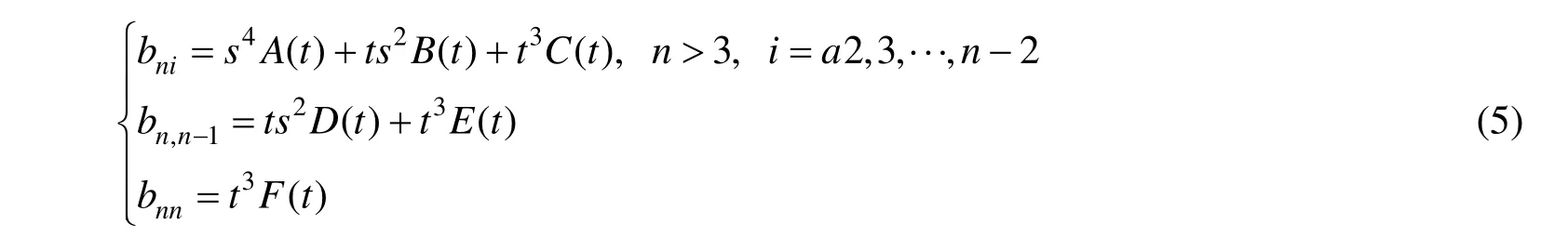
其中：

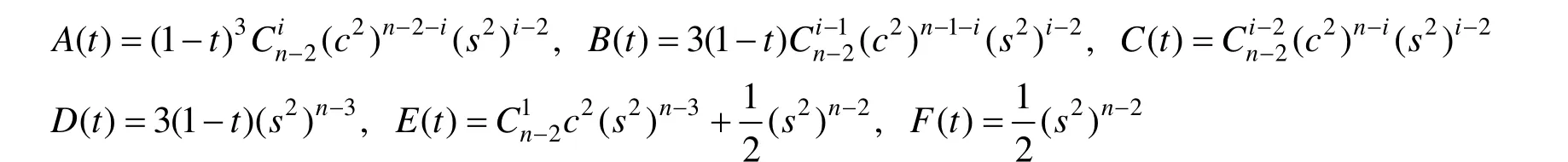
对于两个函数相乘构成的表达式G(t)=H(t)I(t)而言，有：

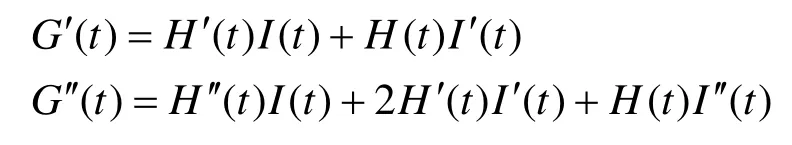
故：

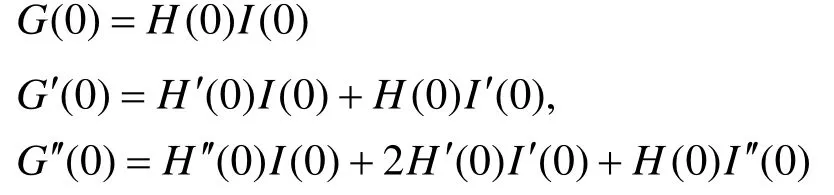
因此只要I(0)=I′(0)=I′′(0)=0，必有G(0)=G′(0)=G′′(0)=0。而注意到s4,ts2,t3在t=0处的函数值、一阶导数值、二阶导数值均为0，故由式(5)和以上分析可知：

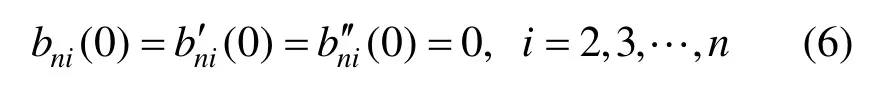
再由式(2)经过计算易知：

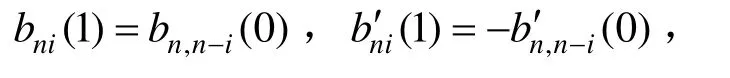
其中n≥2，i=0,1,…,n。由式(3)和式(9)易知式(4)正确。

2 曲线及其性质

2.1 曲线的定义与性质

定义2.给定n+1个控制顶点V∈Rd(d=2,3;i=0,1,…,n;n≥2)，称：

为由混合函数定义的n阶新曲线。

由混合函数的性质，易知新曲线具有如下性质：

(1) 凸包性。由混合函数的非负性和规范性可知，新曲线位于其控制顶点形成的凸包内。

(2) 几何不变性与仿射不变性。由混合函数的规范性可知：一方面，新曲线的形状仅依赖于控制顶点，几何变换不改变曲线的形状；另一方面，对控制多边形进行缩放或错切等仿射变换，所对应的新曲线就是原曲线经过相同仿射变换后的曲线。

(3) 对称性。由混合函数的对称性可知，由控制多边形V0V1…Vn和VnVn-1…V0所生成的曲线形状是相同的，只是方向相反。

(4) 端点性质。由混合函数的端点性质和新曲线的表达式可知，在新曲线的端点处有：

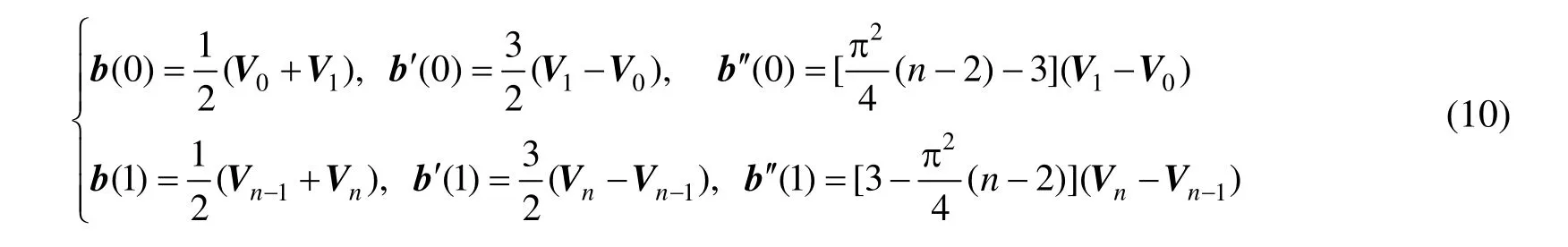
图5～8所示为2～5阶新曲线。从图中可以看出，新曲线插值于控制多边形首末边的中点。另外，新曲线能较好地保持控制多边形的凹凸性等特征。

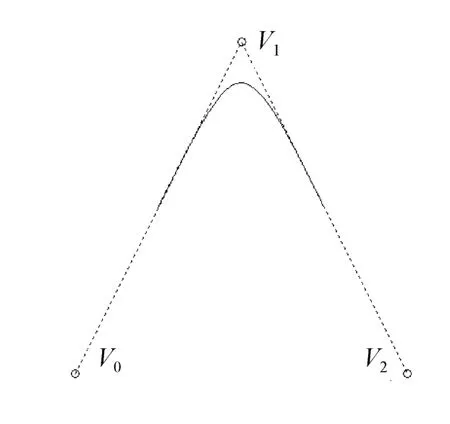
图5 2阶新曲线

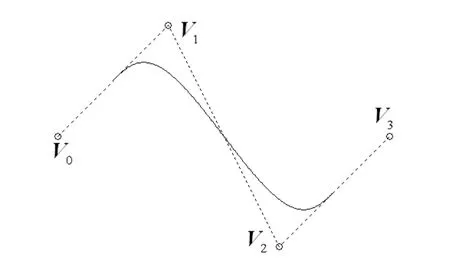
图6 3阶新曲线

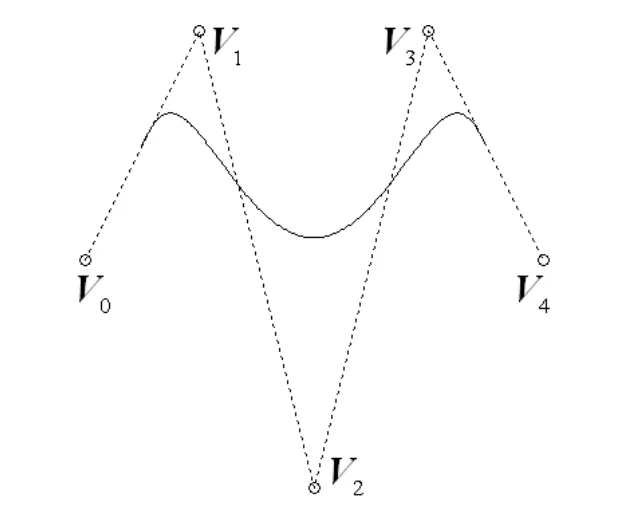
图7 4阶新曲线

图8 5阶新曲线

2.2 组合曲线的连续性

定理1.设有m阶新曲线与n阶新曲线若：

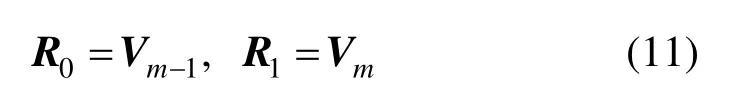
则两曲线G2连续。

证明.由式(10)可知：

在式(11)所给条件下，有：

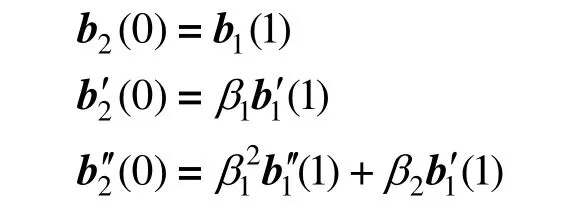
从定理1可知：对于两条新曲线而言，只要前一条曲线的控制多边形的末边与后一条曲线的控制多边形的首边重合，这两条曲线在连接点处便可以达到G2光滑拼接。根据这一特点，对于任意给定的一组控制顶点，可以采用特殊的方式来定义由新曲线构成的分段组合曲线，使之在分段连接点处自动达到G2光滑拼接。

定义3.给定控制顶点V∈Rd(d=2,3;k=0,1,…,l(n-1)+1;l≥1;n≥2)，可以定义一条由l条n阶新曲线构成的分段组合曲线，第i条曲线定义为：

其中，i=1,2,…,l。

定义3中分段曲线的组合方式是不同于传统B样条曲线的。在B样条曲线中，相邻曲线段只有一条控制边或者说一个控制顶点不相同，但是在这里，相邻曲线段只有一条控制边或者说两个控制顶点相同。和B样条曲线一样，这里定义的分段组合曲线也具有局部控制性。但因为定义方式的不同，在这里，移动一个控制顶点至多只会改变两条相邻曲线段的形状。所以很显然，这里给出的组合曲线的局部控制能力优于传统的B样条曲线。

在定义3中，每条分段曲线的阶相同。但实际上，也可以让不同的分段曲线取不同的阶。或者说，可以让不同的分段曲线由不同数量的控制顶点来定义。

定义4.给定控制顶点Vk∈Rd(d=2,3;可以定义一条由l条新曲线构成的分段组合曲线，第i条曲线定义为：

图9～11中所有的分段组合曲线都由相同的控制顶点定义。很显然，由控制顶点构成的控制多边形是左右对称的。按照这里给出的方法，定义出的分段组合曲线(每段曲线上标出的数字为该段曲线的阶)可以是左右对称的(图9～10)，也可以是不对称的(图11)。因此，由同一组控制顶点可以定义出灵活多变的形状(图9～11中还可以增加其他的形状，这里没有一一给出)。

图9 由同阶曲线段构成的对称曲线

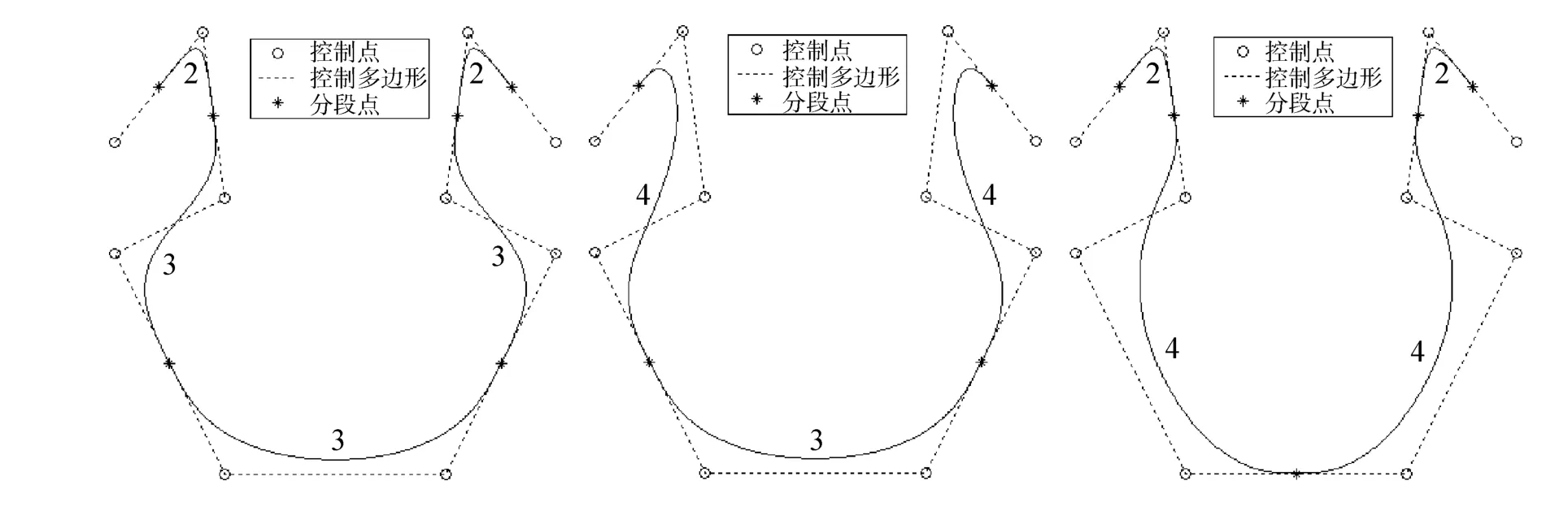
图10 由阶不全相同的曲线段构成的对称曲线

图11 不对称的曲线

2.3 曲线设计

由式(10)和图5～11可以看出，这里定义的新曲线插值于控制多边形首末边的中点而非控制多边形的首末顶点。但是在曲线设计中，常常要求曲线经过控制多边形的首末顶点。为了满足这一需求，可以增加两个辅助顶点V-1=V0，Vn+1=Vn，然后由新的控制多边形V-1V0…VnVn+1定义曲线即可(图12)。如果控制多边形是封闭的(Vn=V0)，那么按照这种方式将得到一条封闭的曲线(图13)，但请注意该曲线在闭合点处并不光滑。如果希望由封闭的控制多边形定义出光滑的封闭曲线，只需增加一个辅助顶点Vn+1=V1即可(图14)。

图15中给出了3个数值例子，其中用到了上一段提到的设计方法。图15(a)中的曲线由两条5阶曲线段组成，曲线经过控制多边形的终点。图15(b)中的封闭曲线由3条曲线段组成(4阶、3阶、4阶)，曲线在闭合点(圆圈+星号标注的点)处不光滑。图15(c)中的封闭曲线由5条3阶曲线段组成，曲线在所有连接点处均光滑。

3 曲面及其性质

定义5.给定控制顶点V∈R3(i=0,1,…,l(m-1)+1;j=0,1,…,l(n-1)+1;ij12l1,l2≥1;m,n≥2)，可以定义一张由l1×l2个m×n阶曲面片构成的组合新曲面，第(i,j)个曲面片定义为：

图12 在开的控制多边形下，从中点插值到端点插值

图13 在闭的控制多边形下，从中点插值到端点插值

图14 在闭的控制多边形下，从开曲线到光滑的闭曲线

图15 组合新曲线的图例

其中，i=1,2,…,l1;j=1,2,…,l2。

定义5中给出的是在最简单的情况下，也就是各张曲面片的阶都相同时的定义。实际上，各张曲面片的阶可以不全相同，只要相邻4张曲面片的阶满足图16中给出的关系即可。

图16 相邻曲面片阶的关系

新曲面具有与新曲线类似的性质。例如，在公共连接边处，组合新曲面2G连续。

图17中给出了由相同控制网格定义的不同的组合新曲面。图17(a)～17(c)中的曲面分别由24张、12张、6张曲面片构成。

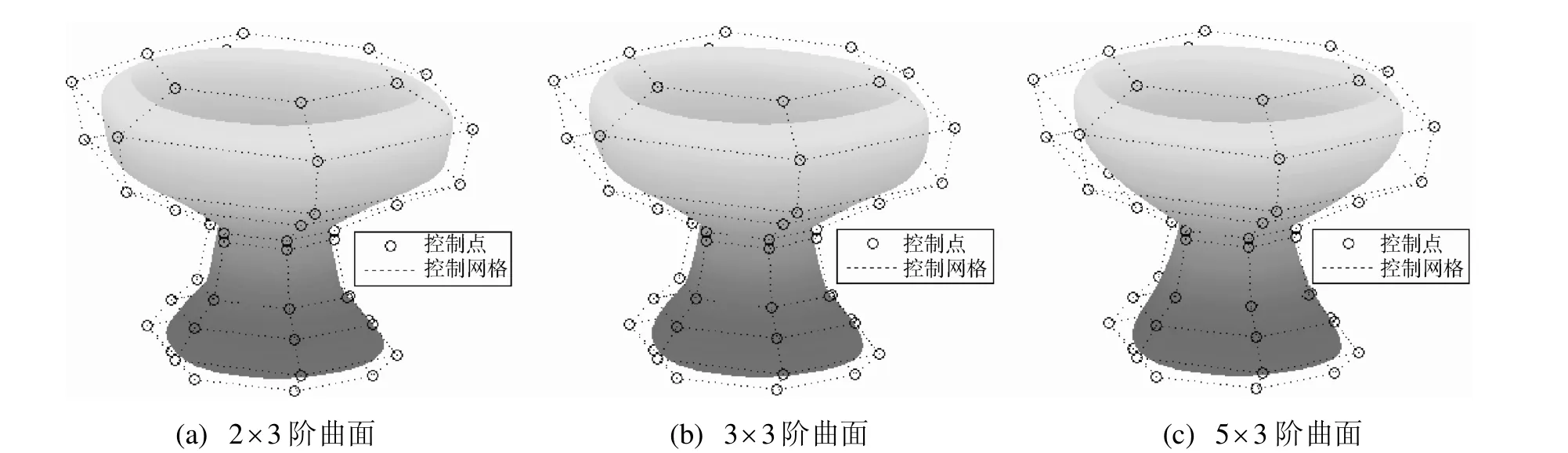
图17 组合新曲面的图例

4 总 结

这里给出的曲线曲面造型方法具有文中提到的很多优点，但它依然存在缺点，主要体现在2个方面：一是传统造型方法都采用多项式函数作为基函数，而这里除了2阶混合函数为多项式函数以外，其它均为代数三角混合函数，所以这里的计算量会有所增加；二是现有很多文献中以代数三角混合函数为基函数的方法能表示一些圆锥曲线曲面和超越曲线曲面，但这里的方法不具备这一性质。因此，下一步至少可以从两个角度来对这里的方法进行改进：一是构造以多项式函数为混合函数的新的曲线曲面，使之具备这里给出的曲线曲面的所有性质；二是构造以代数三角混合函数作为基函数的新的曲线曲面，使之在具备这里给出的曲线曲面的所有性质之外，还能精确表示一些圆锥曲线曲面和超越曲线曲面。

[1] Wang Wentao,Wang Guozhao.Bézier curves with shape parameter [J].Journal of Zhejiang University-SCIENCE A,2005,6A(6): 497-501.

[2] Han Xian,Ma Yichen,Huang Xili.A novel generalization of Bézier curve and surface [J].Journal of Computational and Applied Mathematics,2008,217(1): 180-193.

[3] Yang Lianqiang ,Zeng Xiaoming .Bézier curves and surfaces with shape parameters [J].International Journal of Computer Mathematics,2009,86(7): 1253 -1263.

[4] Yan Lanlan,Liang Jiongfeng.An extension of the Beizer model [J].Applied Mathematics and Computation,2011,218(6): 2863-2879.

[5] Qin Xinqiang,Hu Gang,Zhang Nianjuan,Shen Xiaoli,Yang Yang.A novel extension to the polynomial basis functions describing Bezier curves and surfaces of degree n with multiple shape parameters [J].Applied Mathematics and Computation,2013,223(10): 1-16.

[6] 严兰兰,邬国根.Bézier方法的新扩展[J].合肥工业大学学报(自然科学版),2013,36(5): 625-631.

[7] Han Xuli.Piecewise quadratic polynomial curves with a local shape parameter [J].Journal of Computational and Applied Mathematics,2006,195(1-2): 34-45.

[8] Liu Xumin,Xu Weixiang.Uniform B-spline curve and surfaces with shape parameters [C]//2008 International Conference on Computer Science and Software Engineering,2008,12: 975-979.

[9] Han Xuli.A class of general quartic spline curves with shape parameters [J].Computer Aided Geometric Design,2011,28(3): 151-163.

[10] 夏成林,邬弘毅,郑兴国,彭凯军.带多个形状参数的三次均匀B样条曲线的扩展[J].工程图学学报,2011,32(2): 73-79.

[11] Chen Qinyu,Wang Guozhao.A class of Bézier-like curves [J].Computer Aided Geometric Design,2003,20(1):29-39.

[12] Han Xian,Ma Yichen,Huang Xili.The cubic trigonometric Bézier curve with two shape parameters [J].Applied Mathematics Letters,2009,22(2): 226-231.

[13] 苏本跃,盛 敏.基于双曲函数的Bézier型曲线曲面[J].计算机工程与设计,2006,27(3): 370-372.

[14] 张锦秀,檀结庆.代数双曲Bézier曲线的扩展[J].工程图学学报,2011,32(1): 31-38.

[15] Han Xuli,Zhu Yuanpeng.Curve construction based on five trigonometric blending functions [J].BIT Numerical Mathematics,2012,52(4): 953-979.

[16] Han Xuli.C2quadratic trigonmetric polynomial curves with local bias [J].Journal of Computational and Applied Mathematics,2007,180(1): 171-177.

[17] 严兰兰,梁炯丰.一种带形状参数的三角样条曲线[J].计算机工程与科学,2011,33(5): 69-73.

[18] 严兰兰.带形状参数的三角曲线曲面[J].东华理工大学学报,2012,35(2): 197-200

[19] Yan Lanlan,Liang Jiongfeng.A class of Algebraictigonometric blended splines [J].Journal of Computational and Applied Mathematics,2011,235(6): 1713-1729.

[20] 谢 进,檀结庆.多形状参数的二次双曲多项式曲线[J].中国图象图形学报,2009,14(6): 1206-1211.

[21] Liu Xumin,Xu Weixiang,Guan Yong,Shang Yuanyuan.Hyperbolic polynomial uniform B-spline curves and surfaces with shape parameter [J].Graphical Models,2010,72(1): 1-6.

[22] 张 莉,刘静静,檀结庆.多形状参数的指数均匀B样条曲线曲面[J].图学学报,2013,34(3): 29-35.