应用三次C-Cardinal样条曲线构建的股线模型

赵志祥， 郑天勇，2， 吴 珍， 李婷婷

(1. 中原工学院 纺织学院， 河南 郑州 450007; 2. 河南省纺织服装产业协同创新中心， 河南 郑州 450007)

纱线形态设计一直是纺织CAD设计的核心内容。通过查阅文献发现，对股线[1-2]进行仿真模拟的研究较少，而对单纱仿真设计研究较多，但其成果能为股线的仿真设计提供借鉴。Sripratccp等[3]采用多条非均匀B样条曲线作为单纱中的纤维，取得了较好的单纱仿真效果及纤维在单纱中的内外转移，但由于算法复杂仅应用在单纱设计中。Chen等[4-5]虽给出了复杂织物组织的三维视图，实现了织物结构的空间形态，但纱线简化为单独的一根管状，缺少纱线的捻度及材质效果。国内研究[6-8]中也有采用B样条曲线对单纱形态进行深入探究的，无论从单纱横截面形状还是单纱捻度，都取得了逼真的仿真效果，但算法较为复杂，内存消耗大，需要较高的计算机硬件配置，目前尚不宜应用在股线的仿真设计中。鉴于以上分析，本文采用股线切面叠加法和具有良好插值性的三次C-Cardinal样条曲线[9]，对空间任意弯曲股线进行仿真建模，取得了股线在三维空间中光滑拼接及加捻无错切的仿真效果。

1 C-Cardinal样条曲线及其特点

使用(1tcos(t) sin(t))为基底取代三次样条曲线的基构造的一系列曲线称为三次C-Cardinal样条曲线，其中三次C-Cardinal样条曲线的一般数学定义式如下：

(1)

0≤t≤α,i=0,1,2,…，n-3

式中：bi(i=0,1,2,…，n)为给定的型值点；ωj,α(t)为样条基函数；其他参数定义见文献[10]，曲线段Pi(t)组成的曲线P(t)称为三次C-Cardinal样条曲线。

该曲线算法简单，计算内存消耗少，运算速度快，生成曲线除首尾点外完全插值于给定型值点，是一种既简便又实用的工程造型工具。

2 股线横截面形态建模

2.1 股线中单纱横截面形态简化处理

1)假设股线中单纱横截面为圆形并相切，单纱半径为R；

2)以股线中心O为坐标原点建立直角坐标系。

图1示出3股纱的横截面数学简化模型。圆由一定数量的点经线段连接而成，且在每个点处以其坐标值作为法向量的值，以期获得良好的光照反射效果，提高股线模型的立体感。

图1 圆形横截面 Fig.1 Circular cross section

在基于Open GL图形库的显示屏幕中，设置三维坐标原点位于屏幕中央，Y轴正方向向上，X轴正方向向右，Z轴正方向垂直屏幕指向外侧。在对股线横截面建模时，坐标系沿X轴翻转后，使Y、Z轴坐标系互相调换，保持X轴与坐标系原点不变，同时使股线中心O与坐标系原点重合。图1中，经简化后股线单纱中心的坐标如下。

(2)

(3)

(4)

式中，O1、O2、O3为各单纱的中心点。

当股线合股数在数十股以上时，股线中单股纱线的横截面的半径相对股线横截面半径较小，此时要求股线中单根纱线的横截面排列位置需保证股线横截面形状近似圆形，如此才能得到均匀加捻的股线仿真效果图。

另外，采用三次C-Cardinal样条曲线，可构建椭圆形、跑道圆形及凸透镜形等各种纱线横截面形状，如图2所示。图中较粗线条为横截面轮廓图，较细线条为三次C-Cardinal样条曲线的控制多边形。

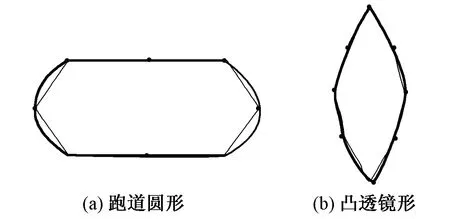
图2 规则纱线横截面模型及其控制多边形Fig.2 Regular yarn′s cross section and their control polygon. (a) Racetrack; (b) Lens

在股线仿真过程中发现，上述横截面由于其边缘圆滑，不能较好地对股线中单根纱线加捻纹理进行仿真，因此对上述横截面加以改进，采用非规则多边形构建股线横截面。

2.2 横截面形态采用非规则多边形处理

1)股线中单纱中心相对于股线中心保持不变,单纱半径仍为R；

2)改变单纱圆形截面，使其圆上的点向外凸出和向内凹陷获得的非规则多边形作为单纱横截面，同样在每个点处设置法向量，如图3所示。同理，可根据股线中单纱横截面的设计需要，设计不同的形状，且当直线段能够满足设计要求时，为减少算法的复杂度及提高仿真效率，股线横截面形态设计一般不采用三次C-Cardinal样条曲线。

图3 非规则多边形横截面Fig.3 Irregular polygon cross section

3 股线中心线表示及股线仿真

3.1 股线中心线表示

股线中心线的设计采用插值性较好的三次C-Cardinal样条曲线，能够精确地控制股线在真实环境中的弯曲路径，实现股线设计效果的所见即所得。在三次C-Cardinal样条曲线上的每一点处，使所绘制的股线横截面经过适当的平移与旋转，确保横截面与股线中心线在该点处的切线相垂直，通过设置适当的节点值，显示出连续的股线外形。股线捻度的控制由股线相邻2个横截面间的距离及2个横截面间相对旋转的角度决定。

T=100α/(360d)

(5)

式中：T为捻度，捻/10 cm；α为2个相邻横截面间相对旋转的角度(角度制)；d为2个相邻横截面间的距离，mm。

在OpenGL平台的屏幕空间三维坐标系中，股线中心线不仅有XOY平面上的弯曲趋势，而且还有Z轴深度的弯曲。为确保股线横截面与股线中心线的走势(切矢)相垂直，将股线横截面弯曲趋势分解为：股线横截面分别绕Z轴和X轴进行旋转，进而实现在三维空间中任意弯曲和横截面光滑顺接的仿真。为直观表示，将当前空间坐标系xyz旋转了一定的角度，如图4所示。图中：p′(i)为股线中心线在第i个节点处的一阶导数；p′(i)z为第i个节点的一阶导数p′(i)在平面XOY内的垂直投影，因其关系到绕Z轴旋转，所以记为p′(i)z，p′(i)x亦同此理；θz、θx分别为股线横截面绕Z轴和X轴旋转的量。为保持股线旋转后要保持其相邻截面地光滑、无错切拼接，θz、θx的计算分别如下。

θz=180/3.14×atan(dy/dx)

(6)

θx=180/3.14×atan(dz/dx)

(7)

式中，dx、dy、dz分别为股线中心线各坐标方程的导数。

图4 空间平移与旋转模型Fig.4 Model of translation and rotation in three-dimensional space

3.2 股线切面叠加法

股线的整体外观可当作一系列切片置于股线中心线各节点处且依次旋转和相互叠加而成，如图5所示。

图5 股线切面叠加原理Fig.5 Superposition principle of ply yarn′s section

试验发现，在显示器像素为1366像素×768像素的显屏中，只要2个相邻切面间的距离小于股线中单纱半径的十分之一，模型位置距屏幕的距离大于股线中单纱半径的10倍，一般都能得到股线的光滑连接仿真效果，并且此法算法简单，运算量小，在一般的计算机配置中都能较好地实现。

3.3 股线仿真效果

图6示出基于股线中单纱横截面为非规则多边形的数学模型设计的三股股线的外观仿真。为体现其空间立体感，使用了OpenGL图形库中的光照效果，其中股线中心线采用了三次C-Cardinal样条曲线。其中，图6(a)股线中心线处在同一平面内，股线形状沿着较细直线所绘的控制多边形弯曲而屈曲，表现出股线设计的所见即所得效果；图6(b)股线中心线在三维空间中任意弯曲。

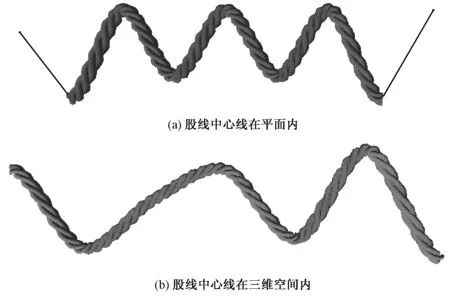
图6 股线仿真效果图Fig.6 Simulation of ply yarn. (a) Centerline in two-dimensional space; (b) Centerline in three-dimensional space

在图6(b)中股线捻度不匀，是由于股线在三维空间中Z轴走向产生的视觉差异，而非真实地出现了捻度不匀，基于此又进一步证实了股线在空间三维中的任意弯曲走向；需特别说明的是在股线弯曲处由于股线相邻横截面间的相对距离缩小，出现捻度略微增大的现象，符合实际情况，且对仿真效果影响可忽略不计。

图7示出了多股股线的仿真效果图。其中图7(a)展现的是多股股线的条干，为直线型，图7(b)显示的为多股股线的横截面示意图。图7(b)中单股线横截面的相对位置较为灵活，但其整体保证了股线横截面轮廓为圆形；同时，股线中单股纱的直径相对于股纱直径非常小，股线横截面形态非常类似于短纤纱中纤维横切面相对于单纱横截面的数量关系，即当股线合股数较多时，股纱仿真形模型近似单纱仿真模型。

图7 多股股线仿真图Fig.7 Simulation of mult-ply yarn. (a) Evenness of mult-ply yarn； (b) Cross section of mult-ply yarn

为展现三次C-Cardinal样条曲线良好的插值性在织物结构中的应用，采用三次C-Cardinal样条曲线插值生成近似于正弦曲线作为股线中心线，以非规则多边形为股线中单纱的横截面，给出了4股股线在平纹织物结构中的应用，并通过对织物的整体旋转，以显示其经纬纱线状态和立体效果，如图8所示。

图8 股线在平纹中的3-D效果图Fig.8 Model picture of ply yarn in plan weave

3.4 本文存在的不足和下一步的工作方向

以圆形作为股线中单纱的横截面与实际情况差别较大，应针对不同材料、类型的股线设计不同的横截面；鉴于切面叠加法操作简便，可尝试其在花式线设计中的应用。

4 结 论

1)文中关于股线中单纱横截面的建模可推广到多股纱，并且单纱横截面的形状可根据设计的需要进行随意的改动，增强了单纱、股线截面设计的灵活性。

2)切面叠加法以股线横截面层层累加而得股线仿真模型，具有方法简便，算法简单，计算量小，应用灵活，仿真效果逼真的优点。

3)三次C-Cardinal样条曲线所具有的良好插值性，方便股线、单纱的中心线弯曲走向的插值逼近，实现股线、单纱设计的所见即所得，提高了仿真效率及效果，可在纺织CAD/CAM中进一步推广应用。

FZXB

[1] 韩祖耀. 股线结构的理论与应用[J].纺织学报, 1982, 3(4): 195-202.

HAN Zuyao. The theory and its application of the structure of ply yarn[J].Journal of Textile Research, 1982, 3(4): 195-202.

[2] 郑天勇. 股线3D模型的建立[J]. 纺织学报, 2002, 23(5): 356-357.

ZHENG Tianyong. Model of the 3D ply yarn[J].Journal of Textile Research, 2002, 23(5)： 356-357.

[3] SRIPRATCCP K, BOHCZ E L J. A new computer geometric modelling approach of yarn structures for theconventional ring spinning process[J]. The Journal of the Textile Institute, 2009, 100(3): 223-236.

[4] CHEN Xiaogang. Mathematical modelling of 3D woven fabrics for CAD/CAM software[J]. Textile Research Journal, 2011, 81(1): 42-50.

[5] LIN Hua, ZENG Xiesheng, SHERBURN Martin, et al.

Automated geometric modelling of textile structures[J]. Textile Research Journal, 2012, 82(16): 1689-1702.

[6] 郑天勇，崔世忠. 用B样条曲面构建纱线三维模型的研究：IV： 具有不同截面的三维纱线模型的构造[J].纺织学报, 2006, 27(2): 53-57.

ZHENG Tianyong, CUI Shizhong. Study on constructing the 3D yarn model by B-spline surface：part IV: construction of the 3D yarn model with different cross sections[J]. Journal of Textile Research, 2006, 27(2)： 53-67.

[7] 郑天勇，崔世忠. 用B样条曲面构建纱线三维模型的研究：II: 纱线捻度的三维模拟[J]. 纺织学报, 2006, 27(3): 24-26.

ZHENG Tianyong, CUI Shizhong. Study on constructing the 3D yarn model by B-spline surface： part II: inserting 3D bumping texture on the surface of the yarn[J]. Journal of Textile Research, 2006, 27(3)： 24-26.

[8] ZHENG Tianyong. Study on general geometrical modeling of single yarn with 3D twist effect[J]. Textile Research Journal , 2010, 80(10): 867-879.

[9] 张纪文, 罗国明. 三次样条曲线的拓广：C曲线[J]. 计算机辅助工程, 1996(3): 12-20.

ZHANG Jiwen, LUO Guoming. C-Curves：an extension of cubic curves[J]. Computer Aided Engineering, 1996(3): 12-20.

[10] 吴晓勤, 严秀坤. 三次C-Cardinal样条曲线及曲面[J]. 计算机工程与科学， 2006, 28(2): 48-50.

WU Xiaoqin, YAN Xiukun. The cubic C-Cardinal spline curve and surface[J]. Computer Engineering & Science, 2006, 28(2): 48-50.